频域子结构方法再推导及环境预示应用研究

陈江攀

（北京电子工程总体研究所，北京 100854）

导弹装备在飞行过程中将承受由发动机推力脉动、喷气噪声以及气动噪声等诱发的振动环境，由于该环境具有宽频带、高强度、随机性大等特点，是导弹装备寿命期内遇到的极为严酷的环境之一[1-2]。恰当制定随机振动环境条件，对于导弹装备的环境适应性设计和地面验证至关重要，条件过低会导致装备难以承受实际飞行环境，进而造成飞行失败，条件过高会导致装备研制难度、周期以及研制经费等增加[3-4]。对于新研型号，由于不确定的因素很多，而可参考的数据又相对匮乏，因此在设计阶段基于仿真技术开展环境预示，以获取弹上典型部位的随机振动响应，对于导弹装备随机振动环境条件的合理制定具有一定的参考价值。

导弹装备结构系统十分复杂，其离散后的有限元模型规模庞大，直接进行仿真分析的计算效率较低。频域子结构方法（FRF-based Substructuring Method，FBSM）的提出与发展有效解决了复杂结构频响函数的计算效率问题，该方法自经提出先后经历了阻抗耦合方法[5]、导纳耦合方法[6]、广义导纳耦合方法[7]和考虑弹性连接的广义导纳耦合方法[8-10]。FBSM 的方法原理为：首先，根据分析需求和结构特征，将整体结构划分成若干子结构；然后，通过试验测量或仿真计算，获得各子结构的频响函数；最后，通过引入界面力平衡和位移协调条件，将各子结构的频响函数进行耦合，获得整体结构的频响函数。由于各子结构可忽略高阶模态影响，利用模态叠加法计算带内频响函数，因此 FBSM 可在满足实际工程应用精度需求的前提下，显著提升计算效率[11]。此外，FBSM 还具有以下优点：1）若某子结构需进行结构优化，则只需获得该子结构优化后的频响函数，即可利用FBSM 与其他子结构重新耦合获得优化后整体结构的频响函数；2）各子结构可由不同单位分别进行设计、分析与测试，最后交由总体单位进行耦合分析，符合导弹装备的研制特点；3）FBSM 的输入为各子结构的频响函数，对获取频响函数的试验方法或仿真分析平台等不作限制[11-12]。需要说明的是，利用FBSM 进行子结构耦合获得的是位移频响函数，而工程中随机振动环境预示通常需要利用加速度传递函数[13]，故亟需开展位移频响函数与加速度传递函数之间的转换关系研究。

文中首先基于 SMW（Sherman-Morrison-Wood bury）公式对考虑弹性连接的FBSM 进行了重新推导，形成了适用范围更广的表达形式。然后，根据线性系统的振动方程推导获得了复杂结构系统的位移频响函数与加速度传递函数之间的转换关系，并据此进一步研究形成了基于FBSM 的随机振动环境预示方法。最后，通过设计仿真算例对文中研究方法进行了仿真验证。论文所得结论可为复杂结构系统的随机振动环境预示提供一定的帮助。

1 考虑弹性连接的FBSM 再推导

1.1 现有方法推导

考虑弹性连接的FBSM 要求将所有子结构和所有弹性连接分别当作一个子结构系统和一个弹性连接系统进行处理[11]，如图1 所示。其中：w和分别为整体结构和子结构系统的内部自由度；u和v、分别为整体结构、子结构系统、弹性连接系统的界面自由度。

根据结构动力学原理，图1 所示的子结构系统和弹性连接系统的位移频响函数矩阵和位移阻抗矩阵分别为：

式中：x、f、H、Z分别为位移向量、力向量、位移频响函数矩阵、位移阻抗矩阵。子结构系统耦合前后，其内部自由度保持不变，见式（3）。同时，引入界面自由度位移协调和力平衡条件，分别见式（4）和式（5）。

由此可得：

将式（7）代入式（6），并整理成矩阵形式可得：

进一步，将式（3）—（5）代入式（1），并整理可得：

此时，将式（8）代入式（9）并进行整理，即可获得整体结构的位移频响函数矩阵HX的表达式为：

上述即为现有考虑弹性连接的FBSM 的推导过程。由式（10）可知，该方法无法直接用于处理具有奇异性位移阻抗矩阵弹性连接系统的子结构耦合问题。

1.2 基于SMW 公式再推导

利用图1 所示的示意图，首先对式（2）中弹性连接系统的位移阻抗矩阵～Z作如下变换：

式中：ZB为变换后矩阵；P和Q均为变换矩阵；I为单位矩阵。将式（11）代入式（2）并整理可得：

又由式（1）、（3）—（5）可得：

进一步，将式（12）代入式（13）并整理可得：

此时，根据结构动力学原理，可得整体结构的位移频响函数矩阵HZ：

观察式（15），其右端与SMW 公式具有相同的表达形式。SMW 公式为[10]：

SMW 公式要求矩阵M和矩阵N均为矩形矩阵，矩阵B为非奇异矩阵[14-15]。由式（11）可知，式（15）中的矩阵P和Q均为矩形矩阵，但矩阵是否为奇异取决于弹性连接系统的动力学特性。为了满足SMW 公式要求，对矩阵进行奇异值分解：

式中：矩阵Δ为矩阵的正奇异值对角阵，为非奇异矩阵；矩阵U和矩阵V均为正交矩阵。将式（17）代入式（15）并整理可得：

式中：矩阵PU和矩阵VTQ均为矩形矩阵，矩阵Δ为非奇异矩阵，满足SMW 公式要求。因此，基于SMW 公式可得整体结构的位移频响函数矩阵HZ的表达式：

上述即为基于SMW 公式考虑弹性连接的FBSM的再推导过程。虽然推导结果与式（10）所示现有方法具有相似的表达式，但通过对比不难看出，文中基于SMW 公式的再推导方法具有以下3 个方面的优势：1）无论弹性连接系统的位移阻抗矩阵是否奇异，该方法均可直接用于处理子结构耦合问题；2）当弹性连接系统的位移阻抗矩阵奇异时，参与求逆运算的矩阵阶数相对更低，具有更高的计算效率；3）推导过程更为简洁，不涉及大量的矩阵运算。

2 随机振动环境预示应用研究

对于线性系统的随机振动，在基础激励作用下的加速度响应计算公式为[16-20]：

式中：下标a和b分别为激励自由度和响应自由度；Sb（ω）为激励自由度的加速度激励功率谱密度；Sa（ω）为响应自由度的加速度响应功率谱密度；Gab（ω）为激励自由度与响应自由度之间的加速度传递函数矩阵；ω为角频率。加速度传递函数矩阵Gab（ω）可通过线性系统在加速度基础激励作用下的振动方程推导获得：

式中：M、C、K分别为线性系统的质量矩阵、阻尼矩阵、刚度矩阵分别为加速度向量、速度向量、位移向量。对式（21）进行展开并整理可得：

对式（22）两端同时进行傅里叶变换[21]并整理可得：

根据结构动力学原理，线性系统的位移频响函数矩阵和位移阻抗矩阵的计算公式为[21]：

将式（25）代入式（24）并整理可得：

式中：Hgz（ω）和Hzy（ω）分别为线性系统在激励自由度为固支状态和自由状态下的位移频响函数矩阵；Zab（ω）为线性系统在激励自由度为自由状态下的响应自由度与激励自由度之间的位移阻抗矩阵。

对于复杂结构系统，为了提高计算效率，位移频响函数矩阵Hgz（ω）和Hzy（ω）均可通过FBSM 计算处理获得。综上所述，基于FBSM 的随机振动环境预示方法如图2 所示。

图2 基于FBSM 的随机振动环境预示方法Fig.2 Environment prediction method for random vibration based on FBSM

3 算例仿真验证

3.1 有限元建模

为了验证基于FBSM 的随机振动环境预示方法的可行性，设计了如图3 所示的仿真算例。该算例由子结构A、子结构B 和子结构C 通过2 个完全相同的弹性连接装配组成，3 个子结构均为空心圆柱体，除长度不同外，其他参数均相同。在子结构A、B 上沿X轴分别均布有3、5 个结点，在子结构C 的两端各布置有1 个结点。模拟实验室随机振动试验，振动工装的装卡位置为结点5 和结点7，激励方向为Y轴，即振动台的随机振动激励通过振动工装作用于结点5和结点7 的Y轴平动自由度，边界条件为结点5 和结点7 的其他自由度固支，振动谱型如图4 所示。

图3 仿真算例Fig.3 Simulation example

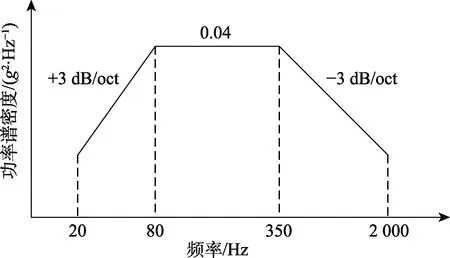
图4 随机振动激励谱型Fig.4 Excitation spectrum of random vibration

利用有限元软件MSC/Patran 对图3 所示仿真算例模拟实验室随机振动试验状态进行有限元建模，其中，3 个子结构利用圆环截面梁单元建模；弹性连接利用无质量圆形截面梁单元等效模拟[22-24]；模型外建立1 个独立结点，并在结点5 和结点7 与独立结点之间分别设置MPC/Rigid 约束；随机振动激励沿独立结点Y轴平动自由度施加，独立结点的其他5 个自由度均设置为固支约束。具体有限元模型如图5 所示，模型参数见表1。

表1 仿真算例有限元模型参数Tab.1 Finite element model parameters of simulation example

图5 仿真算例有限元模型Fig.5 Finite element model of simulation example

3.2 随机振动环境预示

分别利用有限元软件MSC/Nastran 和基于FBSM的随机振动环境预示方法对仿真算例模拟实验室随机振动试验状态下8 个结点（不包括激励结点5 和激励结点7）的Y轴平动自由度的随机振动响应进行了仿真预示和计算预示。仿真预示直接利用有限元软件对图5 所示有限元模型进行计算。在利用FBSM 进行计算预示时，子结构系统和弹性连接系统的模态信息和物理参数均通过图5 所示有限元模型计算获取。其中，由于无质量圆形截面梁单元的刚度矩阵为奇异矩阵，故弹性连接系统的位移阻抗矩阵也具有奇异性[11]，但可利用文中基于SMW 公式再推导获得的FBSM 直接进行耦合分析，体现了该方法的优越性。仿真预示和计算预示结果的对比情况如图6 所示，实线为随机振动激励谱型，点划线为有限元软件仿真预示结果，虚线为基于FBSM 的计算预示结果。由图6 可知，基于FBSM 的计算预示结果与有限元软件的仿真预示结果一致，表明文中所提基于FBSM 的随机振动环境预示方法正确可行。

图6 随机振动环境预示结果对比情况Fig.6 Comparison of prediction results of random vibration environment: a) node 1;b) node 2;c) node 3;d) node 4;e) node 6;f) node 8;g) node 9;h) node 10

4 结论

1）基于SMW 公式，对考虑弹性连接的FBSM进行了重新推导，解决了现有方法无法直接处理具有奇异性位移阻抗矩阵弹性连接系统的子结构耦合问题。

2）推导获得了复杂结构系统的位移频响函数与加速度传递函数之间的转换关系，并据此形成了基于FBSM 的随机振动环境高效预示方法。

3）设计了“模拟实验室随机振动试验”的仿真算例，仿真验证了文中方法的正确性，对于装备的随机振动环境预示具有参考意义。