弹簧应力松弛载荷的在线测量新方法

苏懿，王心雨，冉渭，王梦嘉，宋凯强，贺毅

（1.西华大学 材料科学与工程学院，成都 610039；2.西南技术工程研究所，重庆 400039）

应力松弛是材料在一定温度和固定应变条件下应力随着时间的延长不断降低的现象[1-3]，是弹簧失效的主要形式之一[4-5]，具有渐进性和隐蔽性，容易被忽视，通常会造成严重的损失[6-7]。应力松弛试验是研究应力松弛规律，寻找有效预防措施的基础[8]。因此，改进应力松弛试验方法对于提高应力松弛试验数据的可信度，获得准确的应力松弛规律具有重要的理论及实际意义[9]。

应力松弛试验方法主要有周期试验法和连续测量法2 种[10]。周期试验法作为传统测试方法，是将弹簧装夹在特制的夹具中，试验过程中定期或不定期地将弹簧从夹具中拆卸下来，测量载荷后再装入试验夹具中继续试验，记录每次的载荷值，即可绘制弹簧的应力松弛曲线[11]。采用该方法可以同时测试多种弹簧的应力松弛特性，甚至可以进行成批试验[12-14]，但需要多次装卸，不仅操作繁琐，而且所得试验数据有限，测量误差较大[15]，如果是高温试验，还会引入温度循环，不利于准确反映真实的弹簧应力松弛规律[16]。连续测量法依然采用特制的夹具，通过应力传感器测量施加在弹簧上的载荷，虽然可以在不同温度和应力水平下对弹簧的应力松弛过程进行连续测量[17-19]，但每个传感器只能测定1 个弹簧，测试效率偏低[20]，且传感器与弹簧刚性地串联在一起，遇到振动、碰撞、传感器损坏等外界干扰后，难以恢复。

为了避免周期试验法中的繁琐操作，也为了提高连续测量法的测试效率，结合弹簧的结构特点及加速试验技术的要求，本文提出了一种在应力松弛过程中测量弹簧载荷的新方法，以圆柱螺旋压缩弹簧为例，介绍了新方法的2 种实施方式，不仅提高了试验效率，还有利于获得更加准确的应力松弛试验数据。

1 在线测量原理

弹簧应力松弛是指在总形变量不变的条件下部分弹性变形转变成了塑性变形，进而引起应力降低的现象[21-23]。按照应力松弛的定义，在测量过程中应当保持“总形变量不变”，显然连续测量法是在“总形变量不变”的条件下完成测量的。周期试验法则不然，它突破了“总形变量不变”的限制——将弹簧拆卸下来测量，在拆卸、测量和重新装夹的过程中弹簧的总形变量发生了变化。尽管如此，周期试验法所得数据依然具有重要的价值，且发挥了重要的作用，这表明在测量过程中依然可以让“弹簧的总形变量在短时间内发生变化”。据此，在应力松弛试验过程中，只要将弹簧夹具设计成可动的，测量时使其产生少许位移，完成弹簧载荷–变形量曲线的测试后，可尽快恢复[16]，然后就可以依据载荷–变形量曲线推算出弹簧在装夹状态下承受的载荷。这样既可以避免繁琐的拆卸与装夹过程，减少操作误差，也可以避免测量过程中的温度循环，提高试验数据的可信度。

2 测量装置设计

2.1 单一圆柱螺旋压缩弹簧的测量装置

对于圆柱螺旋压缩弹簧，根据在线测量原理设计了图1 所示的夹具，让夹具的上下夹板间距保持恒定，以保障试验过程中弹簧的形变量恒定。在夹具的上下夹板之间设置可运动的活塞，测量过程中提升活塞，使其离开下夹板，让施加在弹簧上的力全部转移到活塞上。在活塞上串联拉力传感器和位移传感器，即可测量到施加在弹簧上的力与活塞的位移，得到弹簧的载荷–位移曲线。测量后让活塞回到原位，即可让弹簧回到装夹状态，同时使传感器处于非受力状态。经过一段时间的应力松弛试验后，再次提升活塞，并重复上述测量过程，从而实现弹簧载荷的在线测量。

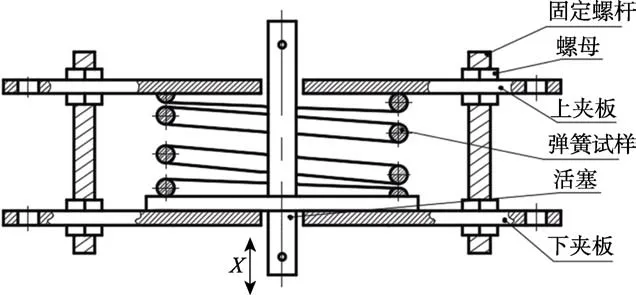
图1 弹簧装夹示意图Fig.1 Schematic diagram of spring clamping

按照应力松弛试验的要求，需要测量的是弹簧处于装夹状态时所承受的载荷，但按照上述的测量原理，测量得到的是弹簧被进一步压缩后所受的载荷，二者之间有一定的差异。因此需要经过适当的计算，才能得到弹簧处于装夹状态时的载荷。

对于螺旋压缩弹簧，其载荷–变形量特性曲线是直线，按照上述测试原理，可得到如图2a 所示的载荷–位移（指活塞的位移x）图。这也是一条直线，经过线性拟合可以得到位移为0 时载荷F0的值，依据F0值，能够换算出弹簧处于装夹状态所承受的载荷。对于数据处理而言，测量过程中活塞的位移x越大，所得到的载荷–位移直线就越长，拟合精度也就越高，这有利于提高测量的准确性。对应力松弛试验而言，活塞的运动是一种干扰，活塞的位移越小，干扰就越小。可见，提高测量精度和减小测量造成的干扰是相互矛盾的。

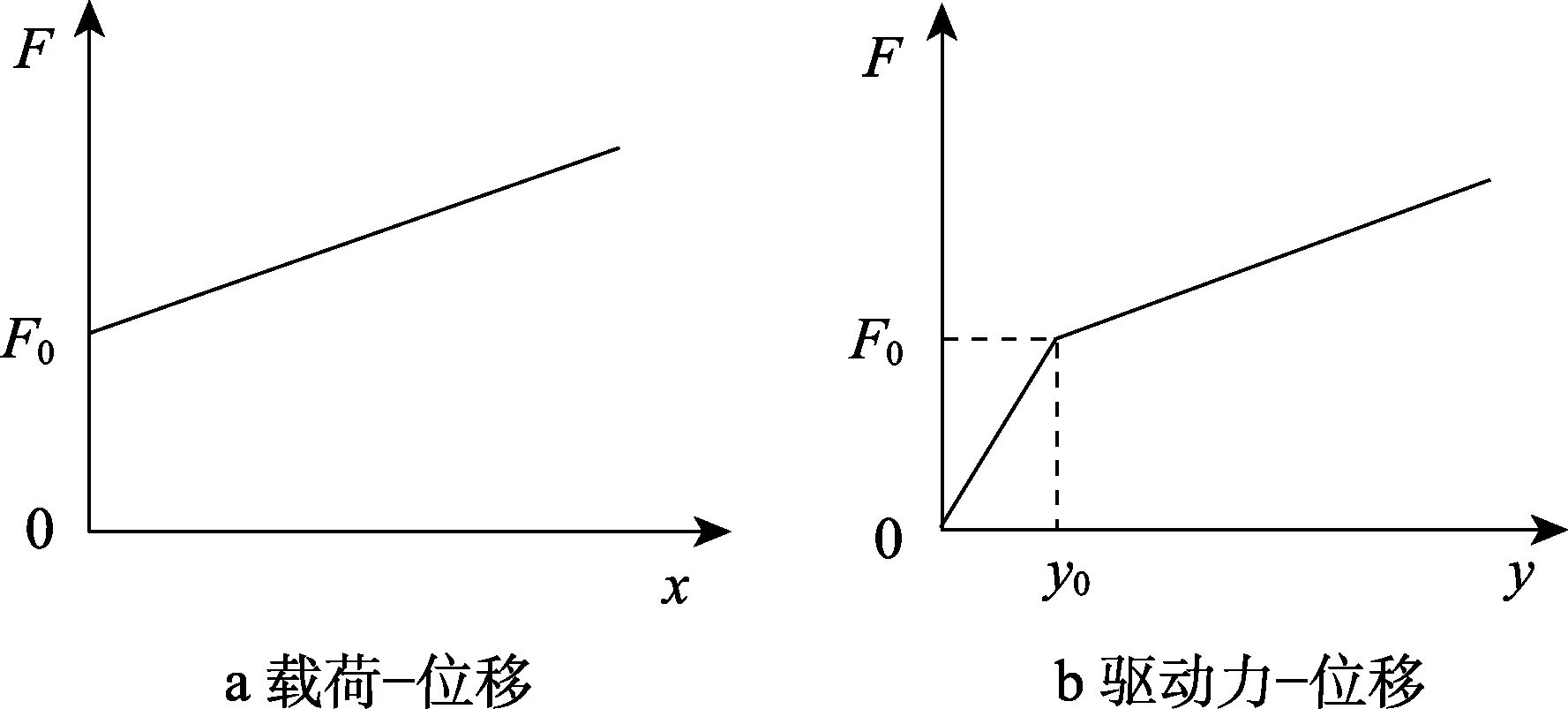
图2 螺旋压缩弹簧的载荷–位移曲线和驱动力–位移曲线Fig.2 Load-displacement curve (a) and driving force-displacement curve (b) of spiral compression spring

为了缓解这对矛盾，在活塞端部增设了一个圆柱螺旋拉伸弹簧作为缓冲弹簧，将外力施加在缓冲弹簧上，通过缓冲弹簧驱动活塞运动，同时测量缓冲弹簧上端的位移，得到如图2b 所示的驱动力–位移曲线。缓冲弹簧的设置如图3 所示。增加缓冲弹簧不仅使活塞运动变得更加平稳[24]，还通过改变测试位移的位置增大了位移量，有利于提高位移测量的准确度。由于缓冲弹簧上端的位移y是活塞位移x与缓冲弹簧的形变量δ之和，所以y既与x线性相关，也与δ线性相关。由图2b 所示的驱动力–位移曲线可见，驱动力F0；当F>F0时，被测弹簧与缓冲弹簧构成组合弹簧[25]，由于叠加了被测弹簧的位移，驱动力–位移曲线开始变得平缓。由此可见，驱动力–位移曲线由2 段直线构成，F=F0时为转折点。分别对2 段直线进行拟合，便可求得转折点的驱动力F0，进而可以计算出待测弹簧处于装夹状态所承受的载荷。可见，增设缓冲弹簧后，只需测量缓冲弹簧上端的位移，不再测量活塞的位移，这有利于减小活塞的位移，进而降低测量对应力松弛过程的干扰。此外，增加缓冲弹簧后，活塞与传感器之间变成了柔性连接，具有一定的减振能力，甚至可以更换传感器，有利于消除外界扰动，有利于提高测试数据的可信度。

采用周期法进行应力松弛试验时，可将弹簧装夹在如图1 所示的夹具中，定期将弹簧连同夹具从试验炉中取出来，按图3 所示的方式测量即可，从而省去了拆装弹簧的繁琐操作。

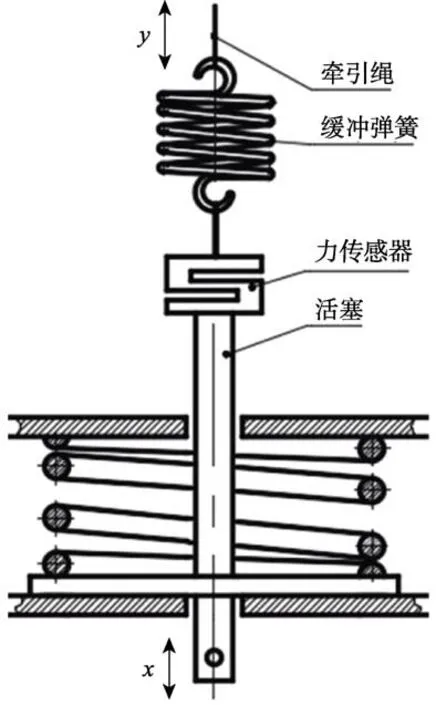
图3 缓冲弹簧设置Fig.3 Schematic diagram of buffer spring setting

2.2 同时测量2 个因素弹簧的装置

对于圆柱螺旋压缩弹簧，如果将2 个待测弹簧串联起来[25]，并对弹簧的位移进行适当的限制（如图4a 所示），则在驱动力–位移曲线上可以出现3 个转折点，如图4b 所示。其中，第1 个转折点对应于活塞离开下夹板时的驱动力（记为F1）；第2 个转折点对应于套筒接触到上夹板时的驱动力（记为F2）；第3 个转折点对应于活塞离开垫板时的驱动力（记为F3）。根据这3 个转折点的驱动力大小，可以计算出弹簧1 和弹簧2 处于装夹状态时所承受的载荷P1和P2。

图4 圆柱螺旋压缩弹簧的串联测量方式及驱动力–位移曲线Fig.4 Tandem measurement method (a) and driving force-displacement curve (b) of cylindrical spiral compression spring

式中：k1和k2依次为弹簧1 和弹簧2 的刚度系数；Δ为套筒与上夹板之间的间隙距离；G1为活塞的重量；G2为垫板的重量；G3为限位套筒的重量。可见，在一次测量过程中，可以同时完成2 个弹簧的载荷测量，进而提高测试效率。

由图3 可见，适当延长夹具中活塞杆的长度，使弹簧和夹具置于试验炉内，同时将传感器和缓冲弹簧置于试验炉外，便可在高温下测量弹簧的载荷。由此设计搭建了如图5 所示的在线测试装置，对于连续测试法样品，既保证了带温连续测量，也可同时完成2个弹簧的载荷测量，提高了测试效率。

图5 测试装置结构Fig.5 Schematic diagram of testing device

3 试验验证与讨论

为了验证上述设计方案和测试装置的可行性，选择了如图6 所示的3 种弹簧。其中，钛合金弹簧用图3 所示装置测量，2 种不锈钢弹簧用图4 所示装置测量。试验中，采用步进电机驱动减速机构提升缓冲弹簧，由于步进电机运行平稳精准，使得提升的距离正比于电机的运行时间，所以没有设置位移传感器，仅记录电机的运行时间便可间接地获得位移信息。

根据上述测试方法和测试装置，测得钛合金弹簧的驱动力–位移曲线如图7a 所示。图中的位移是根据步进电机的运行时间换算出来的，图中曲线出现了明显的转折点，且有较好的线性关系。对转折点两边的线段分别进行线性拟合，得到的拟合曲线如图7b 所示，拟合方程见表1。联合2 个拟合方程，求解得到转折点处的驱动力为127.6 N，减去活塞杆的重量28 N 后，得到钛合金弹簧处于装夹时的载荷为99.6 N。

图7 所示的测试结果虽然是一次测量得到的，且仅能计算出测量时刻弹簧承受的载荷，但该次测量中对2 条直线代表的可变载荷进行了数百次测量。表1中两段直线的相关系数（均大于0.99）和均方差（依次为0.452 4 和0.138 4）表明，测量数据具有较高的可信度。由于测量数据量均大于45，适宜于用正态分布确定测试数据的置信区间。例如对于左侧线段，当置信度为 0.95 时，在线段转折点的载荷区间为(127.6±0.9) N；对于右侧线段，当置信度为0.95 时，在线段转折点的载荷区间为(127.6±0.3) N。由此确定该次测量的结果为(127.6±0.9) N，可见该测量结果具有较高的可信度。

图7 钛合金弹簧的驱动力–位移曲线及拟合曲线Fig.7 Driving force-displacement curve (a) and fitting curve (b) of titanium alloy spring

试验测得不锈钢弹簧的驱动力–位移曲线如图8a所示，出现了3 个转折点，依次对4 条直线段进行线性拟合，得到如图8b 所示的拟合曲线，拟合方程见表2。联合相邻两端线段的拟合方程，求解得到3 个转折点对应的驱动力为：F1=26.1 N，F2=35.7 N，F3=74.7 N。与图7 分析的方法相似，在置信度为0.95时，可以确定3 个测量结果为：F1=(26.1±0.5) N，F2=(35.7±0.4) N，F3=(74.7±0.4) N。根据式（1）和（2），其中，k1=8.9，k2=2.35，活塞重量G1=55.8 N，垫板和限位套筒的重量G2+G3=0.3 N，计算得到装夹下的载荷P1=46.9 N，P2=16.9 N。

图8 不锈钢弹簧的驱动力–位移曲线及拟合曲线Fig.8 Driving force-displacement curve (a) and fitting curve (b) of stainless steel spring

由表1 和表2 可见，所有拟合线的相关系数均高于0.99。在置信度为0.95 时，外推求解得到的转折点的载荷均在±2%以内，说明该拟合曲线和原始载荷驱动力–位移曲线具有较好的相关性。同时也说明，通过上述测量方法和测量装置测得的驱动力–位移曲线具有较高的稳定性。更进一步地，这说明根据拟合结果计算得到的弹簧载荷数据具有很高的可信度。

表2 曲线拟合结果Tab.2 Results of curve fitting

按图1 所示的方式装夹弹簧，采用周期试验法先后对80 余件圆柱螺旋压缩弹簧进行了应力松弛试验，不仅避免了拆卸弹簧，还确保了试验数据的可信度。在连续试验法中，按图3 所示的方式对应力松弛试验中的20 余件弹簧进行了载荷测试，获得了20 多条应力松弛曲线。按照图4 所示的方式装夹图6 所示的2 种不锈钢弹簧，获得了18 条应力松弛曲线，所得数据均能满足试验要求。

4 结论

综合上述分析、设计以及试验验证，在应力松弛试验过程中，可以将待测弹簧承受的准不变载荷转换为缓冲弹簧的连续变化载荷进行测量。在待测弹簧与拉力传感器之间增加缓冲弹簧，有利于提高系统抗干扰的能力。通过驱动力–位移曲线，推算待测弹簧承受的载荷，有利于提高测量结果的可信度。对于圆柱螺旋压缩弹簧而言，借助于固定的上下夹板可以使待测弹簧的压缩量保持恒定，借助于活动的活塞可以使待测弹簧进一步被少量压缩。进一步改进夹具后，还可以将2 个待测弹簧安装在同一夹具试验，从而提高试验与测量效率。