根箭图表示范畴中的Gorenstein平坦-余挠对象

吴德军, 李 丹

(兰州理工大学 理学院, 甘肃 兰州 730050)

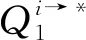
定义1[1]设T是平坦-余挠左R-模的零调复形.若对于任意的平坦-余挠左R-模W,复形HomR(T,W)与HomR(W,T)均正合,则称T为平坦-余挠左R-模的完全零调复形.

定义2[1]设G是左R-模.若存在平坦-余挠左R-模的完全零调复形T,满足Z0(T)=G,则称G为Gorenstein平坦-余挠左R-模.

定义3[2]设F∈Rep(Q,R).若-⊗F是正合函子,则称F为平坦表示.

定义4[2]设Q=(Q0,Q1,s,t)是箭图.考虑顶点集Q0的子集,存在如下超限序列{Vα}(α是序数):

1) 对于第一个序数α=0 设V0=∅;

定义5[2]设Q是箭图.若存在序数λ,使得Vλ=Q0,则称Q是左根箭图.

引理1[2]设R是环,Q是左根箭图.则F∈Rep(Q,R)是平坦表示当且仅当对任意的顶点i∈Q0,以下条件成立:

1)F(i)是平坦左R-模;

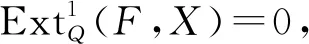
引理2[3]设R是环,Q是左根箭图.则C∈Rep(Q,R)是余挠表示当且仅当对任意的顶点i∈Q0,C(i)是余挠左R-模.

定义7[4]设M∈Rep(Q,R).若存在表示范畴Rep(Q,R)中的平坦表示的正合列…→F1→F0→F-1→…,使得M≅ker(F0→F-1),且对任意的内射表示E,有E⊗Q-作用于上正合列上保持正合,则称M为Gorenstein平坦表示.

引理3[4]设R是环,Q是左根箭图.则M∈Rep(Q,R)是Gorenstein平坦表示当且仅当对任意的顶点i∈Q0,以下条件成立:

1)M(i)是Gorenstein平坦左R-模;

定义10设X∈Rep(Q,R).若X既是平坦表示又是余挠表示,则称X为平坦-余挠表示.

注2所有的平坦-余挠表示类记为FC(Q).

定理1设R是环,Q是左根箭图.则M∈Rep(Q,R)是平坦-余挠表示当且仅当对任意的顶点i∈Q0,以下条件成立:

1)M(i)是平坦-余挠左R-模;

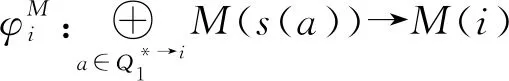
证明由引理1与引理2可得证.

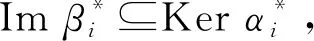
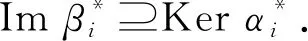
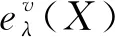
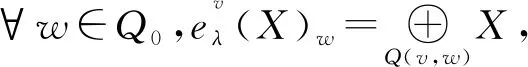
由定义8可知:

则

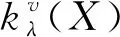
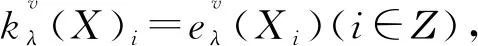
又由定义8可得

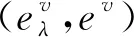
图1 交换图

由定义8与定理1可知,∀v∈Q0,ev(L′)=L′(v)是平坦-余挠左R-模.

定义11设M∈Rep(Q,R).若存在表示范畴Rep(Q,R)中平坦-余挠表示的正合列…→X1→X0→X-1→…,使得M≅coker(X1→X0),且对任意的平坦-余挠表示L,有HomQ(-,L)作用于上正合列上保持正合,则称M为Gorenstein平坦-余挠表示.

注3所有的Gorenstein平坦-余挠表示类记为GFC(Q).

定理2设Q是左根箭图,R是环并且余挠R-模保持直和.则M是Gorenstein平坦-余挠表示当且仅当对任意的顶点i∈Q0,以下条件成立:

1)M(i)是Gorenstein平坦-余挠左R-模;

证明必要性: 因为M是Gorenstein平坦-余挠表示,所以存在表示范畴Rep(Q,R)中平坦-余挠表示的正合列

X:=…→X2→X1→X0→X-1→X-2→…

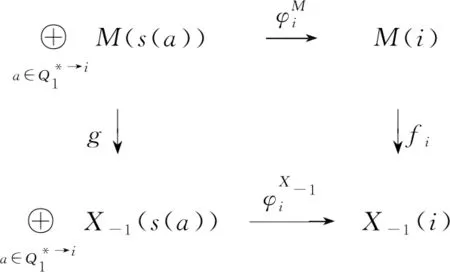
图2 交换图

下证:M(i)是Gorenstein平坦-余挠左R-模.

因为X是表示范畴中的平坦-余挠表示的正合列,且M≅coker(X1→X0),所以由定理1和文献[7]的引理7.11.1后的注记可知,对∀i∈Q0,

是平坦-余挠左R-模的正合列,且

M(i)≅coker(X1(i)→X0(i))

根据Gorenstein平坦-余挠左R-模的定义,下面只需证明:对于任意的平坦-余挠左R-模W,对∀i∈Q0,HomR(X(i),W)正合.

定义表示W′∈Rep(Q,R):

∀i∈V1,W′(i)=W;

∀j∈V1{i},W′(j)=0;

由定理1可知,W′是表示范畴Rep(Q,R)中的平坦-余挠表示.因为M是Gorenstein平坦-余挠表示,所以HomQ(X,W′)=…→HomQ(X-1,W′)→HomQ(X0,W′)→HomQ(X1,W′)→…是正合列.

由命题1可知,有正合列

HomR(X,W′)i=…→HomR(X-1(i),W)→

HomR(X0(i),W)→HomR(X1(i),W)→…

又因为W′(i)=W是平坦-余挠左R-模,所以M(i)是Gorenstein平坦-余挠左R-模.

考虑下列交换图,如图3所示.

图3 交换图

根据Gorenstein平坦-余挠左R-模的定义,下面只需证明:对于任意的平坦-余挠左R-模N,HomR(-,N)作用在图3的第三列保持正合.

对于任意的平坦-余挠左R-模N,用HomR(-,N)作用于图3,则有下列交换图,如图4所示.

图4 交换图

充分性:利用超限归纳法构造复形Xα为表示范畴Rep(Q,R)中的平坦-余挠表示的正合列,且对∀α≤μ(Q)(μ(Q)是指使得Vα=Q0的最小的α),Xα满足下列条件:

1) 对∀i∈Vα(α>0),Xα(i)是平坦-余挠左R-模的正合列,且对任意的平坦-余挠左R-模L,HomR(Xα(i),L)正合;

3) 对∀β<α≤μ(Q),∀i∈Vβ(β>0),Xα(i)=Xβ(i).

下证: 存在表示范畴Rep(Qα+1,R)中的平坦-余挠表示的正合列Xα+1,使得Xα+1满足1)～3).

对∀i∈Vα+1,任意箭头a∈Qα+1且t(a)=i,由定义4后的注1可知,s(a)∈Vα.由归纳假设与已知条件可知:

且存在左R-模中的正合列

因此,存在平坦-余挠左R-模的正合列

使得

由马蹄引理可知,存在M(w)的平坦-余挠左R-模的分解:

同理可得平坦-余挠左R-模的分解:

将上面两个序列连接可得到平坦-余挠左R-模的正合列

使得M(w)≅cokerδ,因为对∀j∈Ζ,任意的平坦-余挠左R-模L,有

是正合的,所以HomR(Xw,L)是正合的.

(3) 当γ<μ(Q)为极限序数时,假设对∀α<γ,存在Xα为表示范畴Rep(Qα,R)中的平坦-余挠表示的正合列且满足1)～3).

下证: 存在表示范畴Rep(Qγ,R)中的平坦-余挠表示的正合列Xγ,使得Xγ满足1)～3).

由假设可知,存在Xβ′是表示范畴Rep(Qβ′,R)中的平坦-余挠表示的正合列并且满足1)～3).

综上,由超限归纳法可知,存在表示范畴Rep(Q,R)中的平坦-余挠表示的正合列X,使得对∀i∈Q0,X(i)是平坦-余挠左R-模的正合列,且满足M(i)≅coker(X1(i)→X0(i)),对任意平坦-余挠左R-模L,HomR(X(i),L)正合.

下证:对任意平坦-余挠表示L′,HomQ(X,L′)正合.

由文献[8]可知,存在平坦-余挠表示复形的短正合列

因为X是平坦-余挠表示的正合列,所以对任意平坦-余挠表示L′,HomQ(X,L′)作用于上正合列保持正合,即

是正合列.

由命题3与直积是正合函子可知:

均正合,因此HomQ(X,L′)正合,由定义11可知,M是Gorenstein平坦-余挠表示.

定义12[7]设Q=(Q0,Q1,s,t)是箭图.若顶点集Q0与箭头集Q1均为有限集,则称Q为有限箭图.箭图Q中的长为l的路p,是指如下有限序列(i|α1,α2,…,αl|j)或简记为α1α2…αl,对任意1≤k≤l,αk∈Q1,有s(α1)=i且t(αl)=j,记为l(p).约定顶点i是起点和终点均为i的长度为零的路,并记为ei.如果l(p)≥1且s(p)=t(p),那么称路p是有向圈,简称为圈.特别地,长度为1的圈称为环圈.若Q不包含圈,则称Q是零调箭图.

推论1设R是环,Q是有限零调箭图.则M是Gorenstein平坦-余挠表示当且仅当对任意的顶点i∈Q0,以下条件成立:

1)M(i)是Gorenstein平坦-余挠左R-模;

证明由定理2可得.