分离函数法在不等式证明题中的应用*

广东省揭阳第一中学(522031) 杨洁珊

在高中教学中,教师如果能引导学生主动深入探究,积极发现并系统总结有效的解题方法,那么学生在学习过程中便能逐步培养思维的深刻性,增加思维的深度,这对提升学生的数学核心素养也有一定的帮助.本文将通过三类典型题,总结如何分离函数,使得不等式证明题的解题过程化繁为简,从而展示分离函数法这个解题技巧的应用.

1 ex与有理函数的组合函数

例1(2018年全国II理,21(1))已知函数f(x)=ex−ax2.若a=1,证明:当x≥0时,f(x)≥1.

证法一当a=1时,f(x)=ex−x2,则f′(x)=ex−2x,f′′(x)=ex−2.令f′′(x)=0,得x=ln2.当x∈[0,ln2)时,f′′(x)<0,f′(x)递减;当x∈(ln2,+∞)时,f′′(x)>0,f′(x)递增.∴f′(x)min=f′(ln2)=eln2−2ln2=2−2ln2>0,故f′(x)>0.∴f(x)在[0,+∞)上递增.∴f(x)min=f(0)=1,故当x≥0时,f(x)≥1.

例1中ex−x2≥1是形如f(x)·ex+g(x)≥0的不等式,其中f(x),g(x)均为有理函数.由于本例中g(x)的次数为2,因此需进行二次求导才能最终达到证明目的.然而,有时一些函数二次求导之后,导函数形式十分复杂,甚至难以判断其正负,从而无法简单完成证明.自然地,我们就会思考这样一个问题,能否找到一个避免二次求导的方法?因此,我们提出以下这个做法:

证法二当a=1时,f(x)=ex−x2.当x≥0时,f(x)=ex−x2≥1等价于(1+x2)e−x≤1.令g(x)=(1+x2)e−x,则g′(x)=2xe−x−(1+x2)e−x=−(x−1)2e−x≤0,故g(x)在[0,+∞)上递减.∴g(x)max=g(0)=1,即当x≥0时,(1+x2)e−x≤1,即f(x)≥1.

由证法二可知,对于形如f(x)·eax+b+g(x)>0的不等式(其中a,b为常数,a0,f(x),g(x))为有理函数)的证明,通过对不等式进行合理的拆分、变形,将eax+b与有理函数结合,构造函数这样可将证明过程化繁为简.此方法还可应用于如下问题:

练习1(2016年全国II理,21(1))证明:当x>0时,(x−2)ex+x+2>0.

解析当x>0时,(x−2)ex+x+2>0等价于令通过求导判断其单调性得g(x)>g(0)=−1即可.

练习2已知函数f(x)=(1−x)ex−1.

(1)求函数f(x)的最大值;

解析(1)通过对f(x)求导判断单调性后可得f(x)的最大值为f(0)=0.

(2)由(1)知,当x>0时,f(x)<0,g(x)<0<1.当−1F(0)=1即可.

另一方面需要注意的是,若不等式f(x)·eax+b+g(x)>0可分离成形如eax+b>kx+m()的不等式,那么我们可直接构造函数F(x)=eax+b−kx−m证明即可,如2010年全国卷II理科20(1):

例2设函数f(x)=1−e−x,证明:当x>−1时,

证明当x>−1时,即1−e−x≥等价于ex≥x+1.令g(x)=ex−x−1,则g′(x)=ex−1.当−10时,g′(x)>0,g(x)递增.∴g(x)min=g(0)=0,故g(x)≥0,即ex≥x+1,即

2 lnx与有理函数的组合函数

例3(2018年全国III理,21(1))已知函数f(x)=(2+x)ln(1+x)−2x.证明:当−10时,f(x)>0.证法一∵f′(x)=ln(1+x)+−2=ln(1+x)+当x∈(−1,0)时,f′′(x)<0,f′(x)递减;当x∈(0,+∞)时,f′′(x)>0,f′(x)递增.∴f′(x)min=f′(0)=0,故f′(x)≥0.因此,f(x)在(−1,+∞)上递增,又f(0)=0,∴当−10时,f(x)>0.

例3中(2+x)ln(1+x)−2x>0是形如f(x)·ln(kx+b)+g(x)>0的不等式,其中k,b为常数,k=0,f(x),g(x)均为有理函数.由于本例中f(x)不为常数(实际上是关于x的一次函数),故需进行二次求导才可最终达到证明目的.同例1,我们依然希望找到一个避免二次求导的解答方法.因此,我们提出以下证法:

证法二令g(x)=ln(1+x)−则g′(x)=≥ 0,故g(x)在(−1,+∞)上递增.又g(0)=0,∴当−10时,g(x)>0,f(x)>0.

由证法二可知,对于形如f(x)·ln(kx+b)+g(x)>0的不等式(其中k,b为常数,k0,f(x),g(x)均为有理函数)的证明,可将ln(kx+b)与有理函数分离,构造函数F(x)=ln(kx+b)+去求导证明.此解题方法还可应用于如下问题:

练习3(2016年全国III理,21(2))证明:当x∈(1,+∞)时,

练习4(2011年新课标全国卷文,21)已知函数曲线y=f(x)在点(1,f(1))处的切线方程为x+2y−3=0.

(1)求a,b的值;(2)当x> 0且x= 1时,求证:

解析(1)可求得a=1,b=1.

3 ex,lnx与有理函数的组合函数

为解决此类问题,我们先来熟悉以下四类常见的函数模型:

(1)函数f(x)=h(x)·lnx,其中h(x)=ax2+bx+c,或h(x)=a,b,c为常数且a,b不能同时为0.特别地,要熟悉y=xlnx,y=x2lnx,y=四个特殊函数的图象:

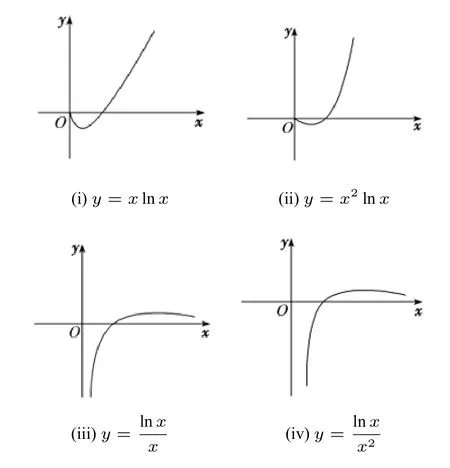
对于以上四类函数,我们需熟悉几个特殊函数的图象特征,特别是其凹凸性.在熟悉的基础上,解题时我们可利用分离函数法将不等式两边通过移项、变形等方法分离出常见的函数模型来处理.

掌握一定的解题方法与技巧可以提高学生的解题能力.当然,我们也要学会灵活变通,比如,并不是所有以上三类问题都需要利用所介绍的分离函数法才可简便解决.近几年,高考命题越来越注重考察学生的数学核心素养,它突出关键能力的考查,强调逻辑推理等理性思维能力,重视数学应用,关注创新意识,渗透数学文化.因此,作为教师,教学时我们要引导学生有意识地从多角度分析问题,锻炼思维的发散性、广阔性,进而提高应用的灵活性,也无形中提升数学核心素养.