质数与合数教学设计
李慧

教学内容:质数与合数
教学目的:
1.使学生理解合数的意义,会判断质数还是合数。
2.培养学生观察、比较、归纳、概括能力。
教学重点:质数与合数的概念。
教学难点:正确判断一个数是质数还是合数。
一、复习导入
1.42÷6=7,()是()的倍数,()是()的因数。
2.教师提问:自然数可分哪两类?
学生答:偶数和奇数。
教师说:自然数还有一种分法,就是按因数的个数来分。
二、板书课题
(一)出示20以内的数。
(二)教师将学生分成4个小组,第一小组写出5以内各个数的因数个数,第二小组写出6—10各个数的因数个数……
(三)让学生根据写出因数个数进行分类。
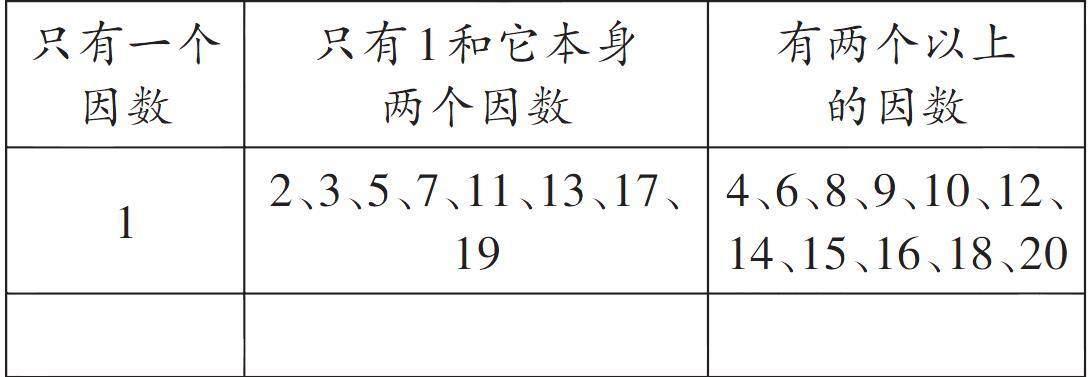
通过学生讨论后汇报上来,教师列表,让学生补充。
(四)教学质数和合数的概念。
1.我们把只有“1”和它本身两个因数的数叫质数。
2.除了“1”和它本身还有别的因数的数叫合数。
3.“1”都不符合上述两个条件,所以“1”既不是质数,也不是合数。
4.教师问:自然数按因数个数来分,分几类?
学生综合归纳:[1和0质数合数]
5.让学生把质数和合数概念读两遍。
三、学会举一反三和观察
(一)让学生观察分类表,回答下列问题。
1.所有的质数是不是一定是奇数?
2.所有的合数是不是一定都是偶数?
3.最小质数是几?最小合数是几?
4.一位数里什么数既是合数又是奇数?
学生一边回答,一边总结。
(二)判断下列各数是质数还是合数。
17、22、29、35、37、87、93、96
(三)出示课本第24页的例1。
1.投影放出1~100以内的数。
2.判断1~100各个数是质数还是合数麻烦吗?很麻烦。
3.让学生用一种快捷的方法找,先划去2的倍数,再划去5的倍数,再划……
4.板书出100以内的质数,强调20以内的质数记下来。
四、巩固练习
(一)填空
1.质数有()个因数,分别是()和();
2.合数至少有()个因数;
3.在1、2、5、7、9、11中()既是质数,又是偶数,()既是合数又是奇数。()既不是质数,也不是合数;
(二)选择正确答案填入括号内
1.两个质数的乘积一定是()
A.奇数 B.偶数 C.质数 D.合数
2.15可以写成哪两个质数和()
A.1和14 B.2和13 C.3和12
3.哪两个相邻的自然数都是合数?
A.3和4 B.5和6 C.7和8 D.8和9
4.m为不为0的自然数,偶数可以用()来表示,奇数可以用()表示。
A.2m+1 B.2m C.m-2
板 书
自然数分为:0和1、质数、合数
20以内质数有:2、3、5、7、11、13、17、19

