适用于强化学习惯性环境的分数阶改进OU噪声
王涛 张卫华 蒲亦非


本文将DDPG算法中使用的Ornstein-Uhlenbeck (OU) 噪声整数阶微分模型推广为分数阶OU噪声模型,使得噪声的产生不仅和前一步的噪声有关而且和前K步产生的噪声都有关联.通过在gym惯性环境下对比基于分数阶OU噪声的DDPG和TD3算法和原始的DDPG和TD3算法,我们发现基于分数阶微积分的OU噪声相比于原始的OU噪声能在更大范围内震荡,使用分数阶OU噪声的算法在惯性环境下具有更好的探索能力,收敛得更快.
DDPG算法; TD3算法; 分数阶微积分; OU噪声; 强化学习
TP39A2023.022001
收稿日期: 2022-03-26
基金项目: 四川省科技计划(2022YFQ0047)
作者简介: 王涛(1997-), 男, 硕士研究生, 四川资阳人, 研究方向为分数阶微积分与强化学习. E-mail: 2647877536@qq.com
通讯作者: 张卫华. E-mail: zhangweihua@scu.edu.cn
An improved Ornstein-Uhlenbeck exploration noise based on fractional order calculus for reinforcement learning environments with momentum
WANG Tao, ZHANG Wei-Hua, PU Yi-Fei
(College of Computer Science, Sichuan University, Chengdu 610065, China)
In this paper, the integer-order Ornstein-Uhlenbeck (OU) noise model used in the deep deterministic policy gradient (DDPG) algorithm is extended to the fractional-order OU noise model, and the generated noise is not only related to the noise of the previous step but also related to the noise generated in the previous K steps in the proposed model.The DDPG algorithm and twin delayed deep deterministic(TD3) algorithm using the fractional-order OU noise model were compared with the original DDPG algorithm and TD3 algorithm in the gym inertial environment. We found that, compared with the original OU noise, the fractional-order OU noise can oscillate in a wider range, and the algorithm using the fractional-order OU noise had better exploration ability and faster convergence in inertial environment.
Deep deterministic policy gradient; Twin delayed deep deterministic; Fractional calculus; Ornstein-Uhlenbeck process; Reinforcement learning
1 引 言
深度Q网络(DQN)[1]的提出开创了深度学习和强化学习结合的先例,DQN算法直接使用了深度神经网络来拟合强化学习中的Q(s,a) 函数,并根据贪心策略选择下一步需要执行的动作,这一工作使得算法在Atari游戏上达到了近似人类玩家的水平.
基于DQN的工作,后续还有人还提出了DDQN[2],Dueling DQN[3],Rainbow DQN[4]等工作,这些工作极大地改进了基于值函数估计类算法的效果.不过,这些工作的动作空间都是离散的,智能体每次只能选择有限的几个动作.然而,在实际的应用场景下,更多的是需要强化学习算法处理连续控制任务.比如无人机追逃控制[5],飞行器高度控制[6],机械臂轨迹规划[7,8],无人机航迹规划[9]等.
对于连续控制任务则无法直接使用DQN系列的算法,研究人员参考DQN系列算法值函数估计的思想,提出了DDPG算法[10],在DDPG算法的基础上又提出了改进的TD3算法[11]、SAC算法[12]和D4PG算法[13].这些算法的提出弥补了基于值函数估计算法在连续空间任务的空白,但是却有着探索能力差的问题,尤其是DDPG算法,由于算法每次输出一个确定性的动作而不是像PPO[14]这样的基于策略梯度的算法一样输出一个正态分布,探索能力会很差.
DDPG系列算法在实际连续控制任务中的使用往往会受到算法探索能力不足的影响,对于一些需要探索的任务,直接使用DDPG系列算法效果并不好.本文结合分数阶微积分理论,对整数阶OU过程进行分数阶推广,使得噪声的产生能够和前K步相关联.实验表明,本文提出的分数阶推广OU噪声模型产生的噪声能够在惯性控制环境下促进DDPG和TD3算法的探索,加快算法收敛,有利于算法在实际控制环境中的应用.
2 相关工作
2.1 DDPG算法
DQN及其衍生算法很好地解决了离散动作空间的强化学习任务,但是却无法处理连续动作空间的任务,如果强行使用这一系列的算法需要对动作空间进行离散化,而离散化又会面临离散动作过多的问题.DDPG算法的作者认为DQN很好地解决了过去一直不看好的使用神经网络拟合Q(s,a)函数的问题,于是在DDPG中借鉴了DQN的离线训练和目标Q网络的思想.
对于离散动作空间的控制,获得了Q(s,a)函数后可以使用ε-greedy策略选取动作,但是在连续空间使用这样的策略却是几乎不可能的事情,为了进行动作选取,DDPG算法借鉴了DPG算法的actor-critic思想,使用策略梯度更新actor,使用贝尔曼等式来更新critic.
由于DDPG的动作选取是一个确定性策略,而不是输出一个策略分布,在连续控制问题上会面临探索不足的问题,文章作者提出了使用Uhlenbeck-Ornstein过程产生的噪声来辅助探索.
OU噪声在惯性环境下的探索能力要强于正态噪声,但是,我们发现通过对OU过程进行分数阶推广产生的分数阶OU噪声在惯性环境下甚至具有更好的探索能力,能够使得离线更新的算法更快地收敛.
2.2 TD3算法
DDPG算法已经能够解决很多连续控制问题,但是除了探索能力不足之外还有错误估计的问题,也就是critic会高估某个状态的Q值,这种估计误差又会进一步地放大,最终影响算法的表现.
TD3算法参考了double-Qlearning[15]的双critic的思想,使用裁剪双Q学习的技巧,也就是通过对两个critic的值取最小值来解决算法高估状态带来的偏差,虽然这样可能会带来低估的问题,但是相比于高估状态带来的后果,低估的问题是可以接受的.
TD3的作者认为,如果算法对状态价值的估计不准确会导致策略网络表现不佳,而较差的策略网络又会进一步导致价值估计不准从而导致算法性能不佳.为了解决这个问题,TD3提出了延迟策略更新(Delayed Policy Update)的技巧,也就是让critic的更新频率高于策略网络的更新频率,通过首先减少critic的估计误差然后再训练策略网络的思想提高算法的性能.
DDPG这样的确定性策略算法每次只输出一个确定性的动作而不是动作分布,这样的算法很容易受到critic估计的误差的影响而导致算法性能下降,为了解决这个问题,TD3借鉴了SARSA算法[16]的思想,首先对动作增加噪声,然后再进行裁剪,使得算法不容易受到critic的误差影响.
TD3算法很好地解决了DDPG算法值函数估计的问题,但是并没有根本上解决DDPG探索不足的问题,文章使用的独立正态噪声能够一定程度上解决探索问题,但是在惯性环境下,独立的正态噪声的探索能力仍然不足,本文提出的分数阶OU噪声能够促进算法在惯性环境下更好地探索收敛得更快.
2.3 分数阶微积分
分数阶微积分是传统的整数阶微积分的推广,和整数阶微积分相比,分数阶微积分更加具有一般性.分数阶微积分有多种定义形式,研究中一般使用Grnwald-Letnikov[17],Riemann-Liouville[18]和Caputo[19]定义式.分数阶微积分具有非局部特性和长时记忆性,使用分数阶微积分推广的模型相比于整数阶的数学模型在图像处理和信号处理[20-22]中往往具有更好的效果.
由于Riemann-Liouville和Caputo定义式是积分形式不易离散化,文章使用G-L定义式来推广OU噪声.离散形式的函数f(x)的v阶导数的G-L定义式如式(1).
算法1首先初始化全局的长度为K 的数组x用于存放生成的噪声,由于初始时刻x中并没有保存历史数据,初始化设定为从标准正态分布中采样.长度为K 的数组mask用于存放分数阶权重模板,初始化为0.计算出权重模板后根据式(9)计算下一个噪声并存入当前index指向的位置.其中,maskx表示权重模板和历史噪声进行卷积,N表示对标准正态分布进行采样x[t]表示上一次的噪声数据.最后对index进行更新重复利用数组x.
4 实验与分析
分数阶OU噪声是一种探索策略,为了测试这种噪声的探索能力,本文选择了离线策略(off-policy)连续控制的经典算法DDPG以及基于DDPG的改进算法TD3进行实验.需要注意的是,我们不选择PPO这样的在线(on-policy)算法是因为探索策略和训练策略差异很大的时候在线算法根本不能训练.
为了证明分数阶OU噪声在具有惯性的环境下能够使得算法更好地探索,本文选择了gym强化学习环境中的经典控制游戏Pendulum-v0和Mountain Car Continuous-v0以及box2d的Lunar Lander Continuous-v2.Pendulum-v0任务要求将一根自然垂下的钟摆立起来,环境的输入状态是钟摆的角度和角速度,环境的动作是驱动钟摆旋转的力矩大小.Lunar Lander Continious-v2的任务是控制着陆器的火箭喷口的方向和力道使得着陆器着陆,消耗的能量越少越好.Mountan Car Continuous-v0则是控制一辆动力不足的小车利用惯性冲上山坡.这个环境是三个环境中最需要探索的一个环境.如果探索得不好,算法将学不到任何关于环境的有用知识,算法控制的小车将会在原点不断地徘徊.
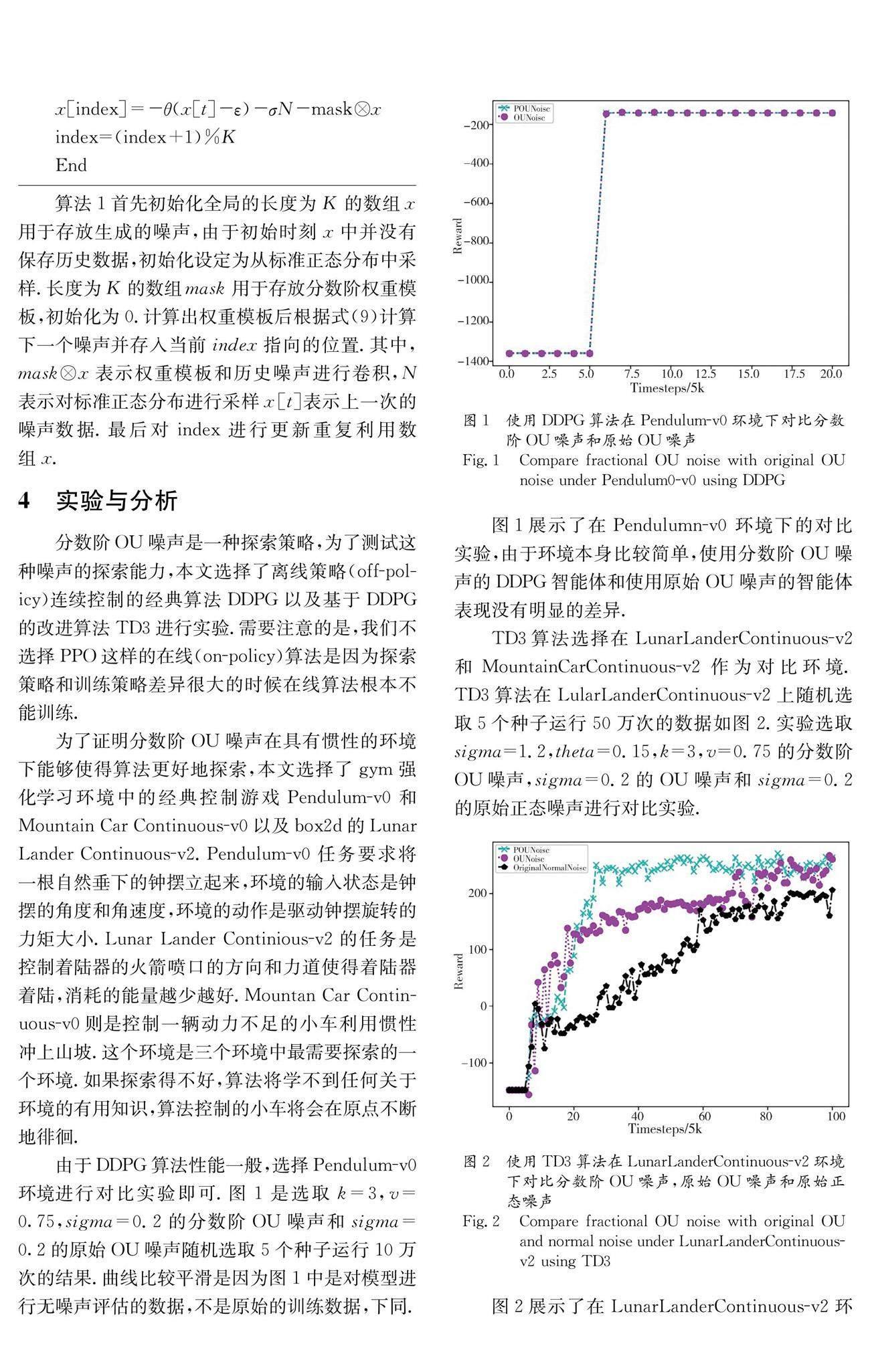
由于DDPG算法性能一般,选择Pendulum-v0环境进行对比实验即可.图1是选取k=3,v=0.75,sigma=0.2的分数阶OU噪声和sigma=0.2的原始OU噪声随机选取5个种子运行10万次的结果.曲线比较平滑是因为图1中是对模型进行无噪声评估的数据,不是原始的训练数据,下同.
图1展示了在Pendulumn-v0 环境下的对比实验,由于环境本身比较简单,使用分数阶OU噪声的DDPG智能体和使用原始OU噪声的智能体表现没有明显的差异.
TD3算法选择在LunarLanderContinuous-v2和MountainCarContinuous-v2作为对比环境.TD3算法在LularLanderContinuous-v2上随机选取5个种子运行50万次的数据如图2.实验选取sigma=1.2,theta=0.15,k=3,v=0.75的分数阶OU噪声,sigma=0.2的OU噪声和sigma=0.2的原始正态噪声进行对比实验.
图2展示了在LunarLanderContinuous-v2环境下的结果,相比于Pendulum-v0,该环境要复杂许多,智能体需要更多的探索.从结果可以看出,使用分数阶OU噪声的TD3智能体表现超过了使用OU噪声和原始正态噪声的智能体,算法收敛得更快.
TD3算法在MountainCarContinuous-v2上随机选取5个种子运行30万次的结果如图3所示.实验选取k=3,v=0.75,sigma=0.6的分数阶OU噪声和sigma=0.6的原始OU噪声以及sigma=0.6的原始正态噪声进行对比实验.
图3展示了在MountainCarContinuous-v0环境下的对比结果.该环境是三个环境中最难的一个,需要最多的探索.从图3中我们可以看到,使用正态噪声的TD3智能体在很长时间内几乎学不到任何知识,获得的奖励一直接近0.而使用分数阶OU噪声和原始OU噪声的智能体则表现得更好更多.可以看出,基于分数阶微积分的OU噪声能够在具有惯性的环境中更好地鼓励强化学习智能体进行探索并更快地学习.
为了探究分数阶OU噪声、OU噪声和正态噪声在惯性环境下的探索能力区别的原因,本文生成了sigma=0.6的三种噪声如图4a~4c.
分析三种噪声可以发现:正态噪声围绕原点在正负两个方向上分布,且靠近原点的噪声点要多于远离原点的噪声点.这表明,如果将正态噪声应用在动作空间上,算法会大量地探索输出动作附近正负两个方向的动作空间,但是对于偏远处动作则很少探索到.
由微分方程可见,OU噪声是一种前后相关的带有回归性质的噪声,也就是说噪声偏离原点越多,下一个噪声就越有可能回归到原点.同时也要注意到,OU噪声虽然会回归到原点,但是在较长的时间段内都是在同一个方向探索.这就决定了使用OU噪声的算法能够在预测动作的某一个方向进行很好地探索,但是对于另一个方向却容易出现欠缺探索的问题.
对于分数阶OU噪声,综合上述图的分析可以发现,分数阶OU噪声不仅具有类似于OU噪声的前后相关和回归性质,还克服了OU噪声容易只探索一个方向的问题.分数阶OU噪声围绕原点进行大范围的且前后相关的探索的性质就决定了使用分数阶OU噪声的算法能够在预测动作的两侧进行足够的探索,在具有惯性的环境下表现得更好.
5 结 论
本文将DDPG算法中使用的基于Ornstein-Uhlenbeck过程的OU噪声进行分数阶推广得到探索能力更强的分数阶OU噪声.通过在Pendulum-v0、LunarLanderContinuous-v2以及MountainCarContinuous-v0环境下进行对比实验,我们发现基于Ornstein-Uhlenbeck过程的OU噪声使得DDPG和TD3算法在惯性环境下比正态噪声具有更好探索能力.而基于分数阶微积分的推广Ornstein-Uhlenbeck过程的分数阶OU噪声,在使得DDPG和TD3算法在惯性环境下更好地探索.这一点上做得比原始OU噪声更好,且使用分数阶OU噪声的TD3算法在惯性环境下能够更好地探索从而更快地学习.
本文还通过分析分数阶OU噪声、原始OU噪声和正态噪声的采样点构成的曲线得出了分数阶OU噪声在惯性环境下探索的更好的原因是分数阶OU噪声能够围绕原点进行自相关的、大范围的探索.
参考文献:
[1] Volodymyr M, Koray K, David S, et al. Human-level control through deep reinforcement learning [J].Nature, 2015, 518: 529.
[2] Hasselt H V, Guez A, Silver D. Deep reinforcement learning with double Q-learning [C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2018: 2094.
[3] Wang Z, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning[C]//International Conference on Machine Learning. SAN DIEGO, CA: JMLR, 2016: 2939.
[4] Hessel M, Modayil J, Van Hasselt H, et al. Rainbow: combining improvements in deep reinforcement learning [C]//Thirty-second AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2018: 3215.
[5] 符小卫, 徐哲, 王辉. 基于DDPG的无人机追捕任务泛化策略设计[J]. 西北工业大学学报, 2022, 40: 9.
[6] 刘安林, 时正华. 基于DDPG策略的四旋翼飞行器目标高度控制[J]. 陕西科技大学学报, 2021, 39: 7.
[7] 张浩博, 仲志丹, 乔栋豪, 等. DDPG优化算法的机械臂轨迹规划[J]. 组合机床与自动化加工技术, 2021, 12: 37.
[8] 张良安, 唐锴, 李鹏飞, 等. 基于复合摆线轨迹的四足机器人稳定性分析[J]. 江苏大学学报: 自然科学版, 2022, 43: 62.
[9] 高敬鹏, 胡欣瑜, 江志烨. 改进DDPG无人机航迹规划算法[J]. 计算机工程与应用, 2022, 58: 264.
[10] Lillicrap T P, Hunt J J, Pritzel A, et al. Continuous control with deep reinforcement learning[J/OL]. [2022-01-28].https://arxiv.org/abs/1509.02971.
[11] Fujimoto S, Hoof H, Meger D. Addressing function approximation error in actor-critic methods[C]//International Conference on Machine Learning. San Diego, CA: JMLR, 2018: 2587.
[12] Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor [C]//International Conference on Machine Learning. San Diego, CA: JMLR, 2018: 2976.
[13] Barth-Maron G, Hoffman M W, Budden D, et al. Distributed distributional deterministic policy gradients[C]//Proceedings of the 6th International Conference on Learning Representations.La Jolla, CA: OpenReview.net, 2018.
[14] Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms [EB/OL]. https://arxiv.org/abs/1707.06347.
[15] Hasselt H. Double Q-learning [C]//Proceedings of the 23rd International Conference on Neural Information Processing Systems. La Jolla, CA: NIPS, 2010.
[16] Sutton R S, Barto A G. Introduction to reinforcement learning [M]. Cambridge: MIT Press, 1998.
[17] Oldham K B, Spanier J. The fractional calculus: integrations and differentiations of arbitrary order[M]. New York: Academic press, 1974: 47.
[18] Samko S G, Kilbas A A, Marichev O I. Fractional integrals and derivatives: theory and applications[M]. Yverdon-les-Bains, Switzerland: Gordon and Breach Science Publishers, 1993: 28.
[19] Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications [M]. San Diego: Elsevier Science & Technology, 1998: 41.
[20] 蒲亦非. 将分数阶微分演算引入数字图像处理[J]. 四川大学学报: 工程科学版, 2007, 39: 9.
[21] 彭朝霞, 蒲亦非. 基于分数阶微分的卷积神经网络人脸识别[J]. 四川大学学报:自然科学版, 2022, 59: 35.
[22] 蒲亦非, 余波, 袁晓. 类脑计算的基础元件:从忆阻元到分忆抗元[J]. 四川大学学报:自然科学版, 2020, 57: 8.
[23] Uhlenbeck G E, Ornstein L S. On the theory of the brownian motion[J]. Phys Rev, 1930, 5: 823.

