基于摩擦和温度修正的Ti-6Al-4V钛合金热变形本构模型建立

吕孝根 向伟 邓浩 罗恒军 邓建伟 袁武华 陈龙庆

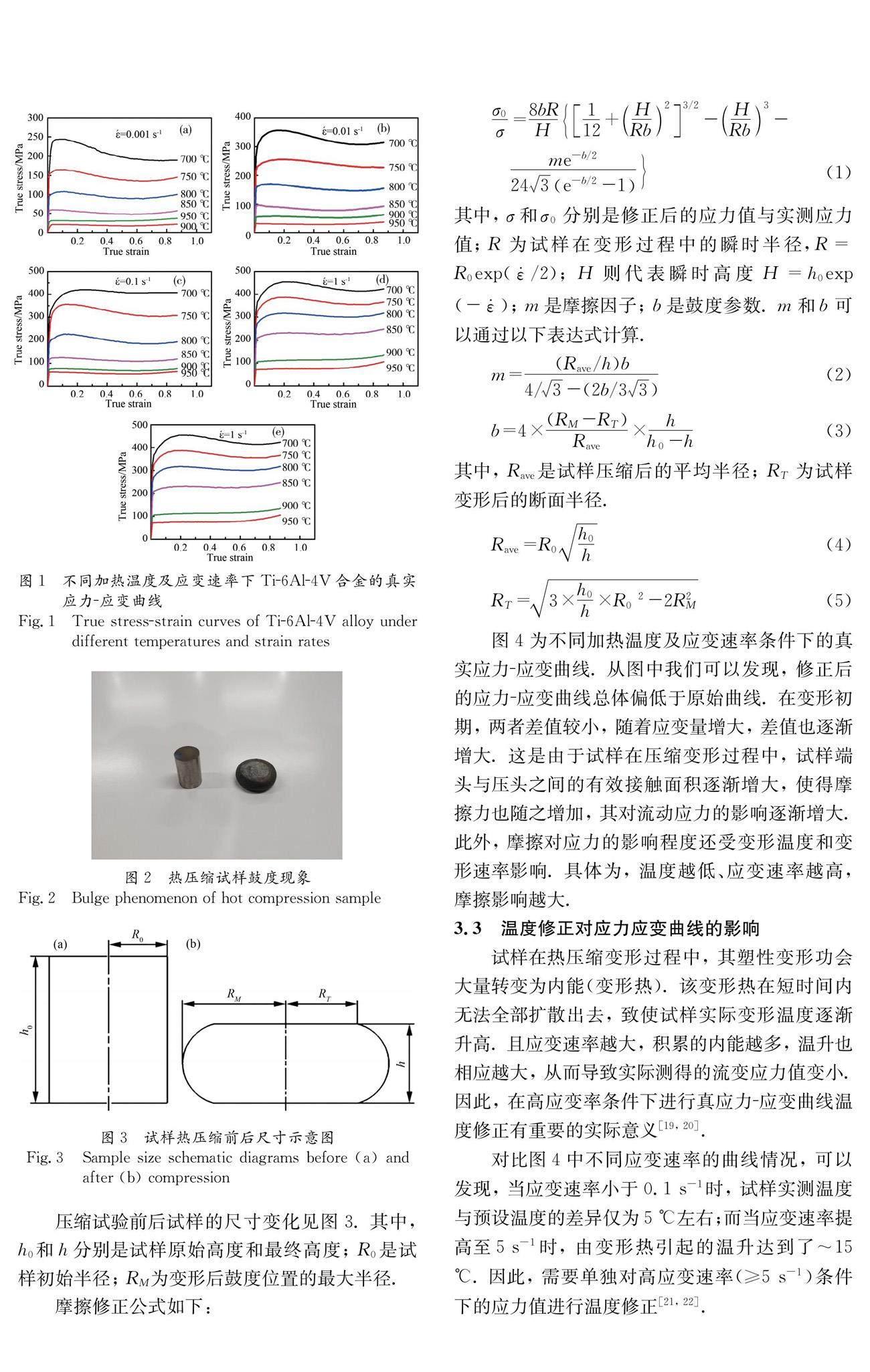
Ti-6Al-4V是民航客机应用最广泛的中高强度钛合金， 在锻造领域， 数值模拟准确性依赖于高准确度的材料模型. 本工作基于热压缩模拟方法， 在不同变形温度（750、800、850、900和950 ℃）和应变速率（0.001、0.01、0.1、1和5 s-1）下， 针对变形量为60%的Ti-6Al-4V合金， 考虑鼓度因素影响， 对真实应力-真实应变曲线进行了摩擦和温度修正， 并进一步构建了该工况条件下的本构模型. 对比实验结果， 修正后的流变应力值低于实际测量值， 且随着应变量和应变速率的提高、变形温度的降低， 二者之间的差值也逐渐增大. 本工作分别建立了Ti-6Al-4V双曲正弦式以及用Z参数表达的材料本构模型. 真实应力应变曲线的摩擦和温度修正对提高材料模型的准确性具有指导意义， 同时对提高数值模拟精度具有参考价值.

Ti-6Al-4V； 摩擦修正； 温度修正； 本构模型

TG142A2023.025002

基金项目： 四川省科技厅重点研发计划（2022YFG0102， 2021YFH0174）

作者简介： 吕孝根（1989-）， 四川资中人， 硕士， 主要研究方向为材料成形. E-mail： 13403461420.@163.com

通讯作者： 陈龙庆. E-mail： chenlongqing@scu.edu.cn

Establishment of thermal deformation constitutive model of Ti-6Al-4V titanium alloy based on friction and temperature correction

L Xiao-Gen1， XIANG Wei 1，2， DENG Hao1， LUO Heng-Jun1， 2，

DENG Jian-Wei2， YUAN Wu-Hua2， CHEN Long-Qing3

（1. Deyang Wanhang Die Forging Co.， Ltd.， China Second Heavy Machinery Group， Deyang 618000， China；

2. School of Materials Science and Engineering， Hunan University， Changsha 410082， China;

3. Key Laboratory of Radiation Physics and Technology， Ministry of Education， Institute of Nuclear Science and Technology， Sichuan University， Chengdu 610064， China）

Ti-6Al-4V is the most widely used medium to high strength titanium alloy for civil airliners. In the field of forging， the realization of reliable numerical simulation depends on a highly accurate material model. Based on the thermal compression simulation method， the present work proposes the friction and temperature corrections for the true stress-real strain curves by considering the effect of the bulge factor under different deformation temperatures （750， 800， 850， 900 and 950 °C） and strain rates （0.001， 0.01， 0.1， 1 and 5 s-1）. The intrinsic model under the working condition is further constructed. The experimental results show that the original measured value is significantly higher than the corrected flow stress value， and the discrepancy between them enlarges with the increase of the strain， the decrease of the deformation temperature and the increase of the strain rate. The hyperbolic sine form and the material constitutive model expressed by Z parameter are established. The friction and temperature corrections of the true stress-strain curve are of guiding significance for improving the accuracy of the material model， and provides reference for improving the accuracy of numerical simulation.

Ti-6Al-4V; Friction correction; Temperature correction; Constitutive model

1 引 言

钛合金具有比强度高、抗腐蚀、耐疲劳和高温性能好等优异的综合性能， 因此在航空航天、船舶和兵器等领域被广泛应用， 有“太空金属”的美称［1-4］. 目前钛合金已成为各类航空器关键承力结构件、发动机核心部件甚至起落架首选的材料之一， 在各国军、民用飞机上的使用量显著增加， 代表了一个国家在国防工业以及机械制造领域的领先程度［5］. Ti-6Al-4V是美国于1954年开发的一种中高强度钛合金（α+β）， 热加工窗口宽， 综合力学性能良好， 且具有优异的耐热、耐腐蚀和易焊接性能［6，7］. 该合金在航空航天、医学器械、体育和汽车制造等众多行业受到青睐［8-11］， 综合使用量已超过钛合金总量的一半.

Ti-6Al-4V合金的优化锻造工艺开发通常依托于传统的“试错法”. 这种方法周期长、成本高. 而基于有限元法的热成形数值模拟分析， 能够实现在极小成本投入的条件下， 以热成形中的金属流动规律、温度场、应变场、缺陷产生、组织演变和载荷变化等信息为指导进行迭代优化， 最终获得最佳的热加工工艺制度［12，13］. 高精度的数值模拟可实现产品制造全流程的可预测及可控制， 减少经济及时间成本［14-16］， 因此建立准确的材料模型是很有必要的.

本文对变形量为60%的Ti-6Al-4V进行了热模拟压缩试验， 得到了不同变形温度（750、800、850、900和950 ℃）和应变速率（0.001、0.01、0.1、1和5 s-1）下的真实应力-真实应变曲线， 在考虑鼓度因素的情况下进行了真实应力-真实应变曲线摩擦和温度的修正， 推导建立了本构模型. 基于摩擦和温度修正的Ti-6Al-4V钛合金热变形本构模型的建立， 对于提高数值模拟的准确性具有重要的指导意义.

2 实验方案

Ti-6Al-4V合金原材料取自万航模锻有限责任公司现场坯料， 其准确成分列于表1. 力学试样采用电火花线切割（DK7732）结合精密车床（36机）加工获得， 试样尺寸为φ10 mm×15 mm. 热压缩实验在热模拟试验机上进行（Gleeble 3800）. 实验过程中， 在试样中间提前焊上热电偶以获得实时变化的温度值， 同时试样端头都采用钽片包裹住以减小试样与压头之间的摩擦系数. 变形温度为700、750、800、850、900和950 ℃， 应变速率为0.001、0.01、0.1、1和5 s-1， 变形量为60%（对应真实应变为0.91）. 测试过程中， 升温速率为10 ℃/s， 试样加热至既定温度后保温3 min再进行力加载， 目的是使试样整体温度均匀. 根据既定的应变速率进行压缩变形试验， 变形结束后采用压缩空气使试样冷却至室温.

3 实验结果与分析

3.1 原始真实应力-应变曲线

不同温度及应变速率下的真实应力-应变曲线绘制于图1. 在热变形初期， 位错的大量生成、扩散与塞积迅速导致加工硬化， 表现为流变应力随应变量急剧增大. 随着位错密度的不断增大， 真实应力迅速达到峰值. 随着变形程度增大， 由动态回复以及动态再结晶导致的动态软化现象开始发生， 位错密度下降， 抵消了部分加工硬化， 流变应力开始下降. 变形量继续增加， 动态软化与加工硬化达到动态平衡， 位错密度基本恒定， 表现为流变应力趋于稳定.

3.2 摩擦修正对应力应变曲线的影响

试样在变形过程中， 由于摩擦因素的影响， 会发生如图2所示的鼓度现象. 这将导致流变应力测试值精度降低. 因此在考虑鼓度因素的情况下对真实应力值进行摩擦修正非常有必要［17，18］.

压缩试验前后试样的尺寸变化见图3. 其中， h0和h分别是试样原始高度和最终高度； R0是试样初始半径； RM为变形后鼓度位置的最大半径.

摩擦修正公式如下：

σ0σ=8bRH112+HRb23/2-HRb3-

me-b/2243e-b/2-1（1）

其中， σ和σ0分别是修正后的应力值与实测应力值; R为试样在变形过程中的瞬时半径，R=R0exp（ε˙/2）; H则代表瞬时高度H=h0exp（-ε˙）; m是摩擦因子; b是鼓度参数. m和b可以通过以下表达式计算.

m=（Rave/h）b4/3-（2b/33）（2）

b=4×（RM-RT）Rave×hh0-h（3）

其中， Rave是试样压缩后的平均半径; RT为试样变形后的断面半径.

Rave=R0h0h（4）

RT=3×h0h×R02-2R2M（5）

图4为不同加热温度及应变速率条件下的真实应力-应变曲线. 从图中我们可以发现， 修正后的应力-应变曲线总体偏低于原始曲线. 在变形初期， 两者差值较小， 随着应变量增大， 差值也逐渐增大. 这是由于试样在压缩变形过程中， 试样端头与压头之间的有效接触面积逐渐增大， 使得摩擦力也随之增加， 其对流动应力的影响逐渐增大. 此外， 摩擦对应力的影响程度还受变形温度和变形速率影响. 具体为， 温度越低、应变速率越高， 摩擦影响越大.

3.3 温度修正对应力应变曲线的影响

试样在热压缩变形过程中， 其塑性变形功会大量转变为内能（变形热）. 该变形热在短时间内无法全部扩散出去， 致使试样实际变形温度逐渐升高. 且应变速率越大， 积累的内能越多， 温升也相应越大， 从而导致实际测得的流变应力值变小. 因此， 在高应变率条件下进行真应力-应变曲线温度修正有重要的实际意义［19， 20］.

对比图4中不同应变速率的曲线情况， 可以发现， 当应变速率小于0.1 s-1时， 试样实测温度与预设温度的差异仅为5 ℃左右；而当应变速率提高至5 s-1时， 由变形热引起的温升达到了～15 ℃. 因此， 需要单独对高应变速率（≥5 s-1）条件下的应力值进行温度修正［21， 22］.

ΔT=0.95η∫ε0σdερCp（6）

其中， ΔT是温度变化量; η是绝热校正系数（ε˙＝5 s-1时， η=1）; ∫ε0σdε是机械功；ρ是密度（4.95 g/cm3）; Cp是比热容（1.7 J/（g·K））.

对变形条件为700 ℃ 5 s-1、700 ℃ 1 s-1以及750 ℃ 5 s-1的摩擦修正后的流变应力进行温度修正， 结果如图5所示. 其中， 虚线对应的流变应力经过了摩擦和温度修正， 实线则仅采用了摩擦修正. 从图中我们可以看出， 随着温度的降低、应变速率的增大， 经温度和摩擦同时修正的应力幅值明显增大. 在700 ℃ 5 s-1变形条件下， 应变为0.9时， 温度修正幅值达到了130 MPa左右.

3.4 修正后的真实应力-应变曲线

在上述工作基础上， 我们进一步对不同变形温度和应变速率条件下的真应力-应变曲线都进行了摩擦-温度修正， 结果如图6所示.

3.5 本构方程的构建

使用由Sellars和Tegart ［23］提出Alpine方程的双曲正弦形式， 如式（7）所示.

ε·=A［sinh（ασ）］n·exp（-QRT）（7）

其中， ε·表示应变速率; A为常数; α为应力因子（mm2 ·N-1）; σ代表流变应力（MPa）; n是应力指数; T是变形温度表达式; Q是物质的热活化能（kJ/mol）；R是气体常数（通常为8.314 J/（mol·K））. 其中， 峰值应力值可从图6中直接读出， 其具体数值列于表2.

当ασ ＜ 0.8时， 可以将式（7）可转变为式（8）；当ασ＞1.2时， 可以将其转变为式（9）. 其中， α=β/n1.

ε·=A1σn1（8）

ε·=A2exp（βσ）（9）

首先， 对上述两个两个公式等号两侧同时取对数， 分别得到以下两个等式.

lnε·=n1lnσp+lnA1（10）

lnε·=βσp+lnA2（11）

其次， 将表2中的峰值应力数值分别带入上述两个公式， 用Origin软件对σp-lnε·和lnσp-lnε·之间的关系进行拟合（见图7）. 式（10）和式（11）中的常数可以根据图中的z斜率和截距求出， 经计算可知n1=6.800 330 949， β=0.044 517 232， 则α=β/n1=0.000 654 633 3.

接着， 再对式（7）两边同时取对数， 即

lnε·=nln［sinh（ασ）］-Q/（RT）+lnA（12）

流动应力、应变速率和变形温度三者之间的函数关系满足双曲正弦公式， 如式（10）所示， 修正后数值可通过式（12）计算得出.

利用Origin软件对ln［sinh（ασ）］-lnε·和ln［sinh（ασ）］-1/T的关系进行线性拟合， 结果如图8a和8b所示. 读取图中的斜率可以求得Ti-6Al-4V钛合金的应力指数n=4.286 540 976， 图8b拟合的斜率值k=15 664.555 84， 将气体常数R代入上述公式， 可以得到Ti-6Al-4V钛合金的热变形激活能为Q=nRk=546.575 kJ/mol.

对于高温变形试验， 可通过Z参数的函数形式来表示材料应变速率与变形温度之间的关系（参数Z表示温度补偿后的应变速率因子［24］）， 即

Z=ε˙exp（Q/RT）（13）

结合式（7）可得：

Z=A［sinh（ασ）］n（14）

两边取对数可得：

lnZ=lnA+nln［sinh（ασ）］（15）

根据前面获得的Ti-6Al-4V合金激活能Q值（546.575 kJ/mol）， 结合式（13）便能计算出不同变形条件下的Z参数值. 进一步对lnZ-ln［sinh（ασ）］关系进行拟合， 结果如图9所示. 显然， 该曲线拟合度较高（线性相关系数达到0.984）， 说明修正系数较为准确. 同时图中还能得到曲线的截距， 即lnA=57.777， 计算得到A=1.23676×1025. 综上所述， Ti-6Al-4V合金在本工作工况条件下的各种具体参数为：α=0.006 546 333， n=4.286 540 976， A=1.23676×1025， Q=546.575 kJ/mol.

因此， Ti-6Al-4V合金热变形试验的Z参数表达式为：

Z=ε˙exp（Q/RT）=Asinh（ασp）n=1.23 676×

1025sinh（0.006 546 333 σp）4.286 540 976（16）

或用Z参数表达材料的流变应力值σ：

σ=α-1ln{（Z/A）1/n+［（Z/A）2/n+1］1/2}（17）

最后， Z参数函数形式可用以预测Ti-6Al-4V合金的流变应力：

σ=152.7573ln{（Z/1.236 76×1025）1/4.286 540 976+

［（Z/1.23 676×1025）2/4.28 654 0976+1］1/2}（18）

4 结 论

本文首先对Ti-6Al-4V合金进行了变温、变应变速率的热压缩模拟试验， 并获得了一系列真实应力-应变曲线. 在考虑鼓度影响的情况下对曲线进行温度和摩擦校正， 以此建立出本构模型， 并得出以下结论.

（1） 摩擦和温度修正的结果显示， 相较于原始测量值， 修正后的应力值总体偏低， 该偏差与应变量和应变速率正相关， 与变形温度负相关.

（2） 获得了Ti-6Al-4V合金在本工作工况条件下的热变形方程：

ε˙=A［sinh（ασ）］n·exp（-QRT） =1.237×1025·

［sinh（0.006 546 33σ）4.286 541］exp（-546 575RT）.

参考文献：

［1］ 赵永庆， 葛鹏， 辛社伟. 近五年钛合金材料研发进展［J］. 中国材料进展， 2020， 39： 527.

［2］ 何丹琪， 石颢. 钛合金在航空航天领域中的应用探讨［J］. 中国高新技术企业， 2016， 27： 50.

［3］ 刘全明， 张朝晖， 刘世锋， 等. 钛合金在航空航天及武器装备领域的应用与发展［J］. 钢铁研究学报， 2015， 27： 1.

［4］ 李梁， 孙健科， 孟祥军. 钛合金的应用现状及发展前景［J］. 钛工业进展， 2004， 21： 19.

［5］ 毛小南， 赵永庆， 杨冠军. 国外航空发动机用钛合金的发展现状［J］. 稀有金属快报， 2007， 26： 1.

［6］ 李毅， 赵永庆， 曾卫东. 航空钛合金的应用及发展趋势［J］. 材料导报， 2020， 34： 280.

［7］ 师俊峰， 韩珍梅. 航空紧固件钛合金材料的应用现状［J］. 机械管理开发， 2020， 35： 258.

［8］ 高天悦. 体育器械用TC4钛合金的力学与耐磨性能研究［J］. 合成材料老化与应用， 2021， 50： 112.

［9］ 宋西平. 钛合金在汽车零件上的应用现状及研发趋势［J］. 钛工业进展， 2007， 24： 9.

［10］ 孟祥军， 汪汀. 船用钛合金发展概况［J］. 钛工业进展， 2000（5）： 7.

［11］ 孙建刚， 宋德军. 国内外石油、天然气用钛合金研究及应用概况［J］. 材料开发与应用， 2019， 34： 96.

［12］ 聂蕾. TC4合金的热模锻过程设计与质量控制［D］. 西安： 西北工业大学， 2002.

［13］ 李潇. 某飞机用钛合金结构件模锻成形工艺研究［D］. 秦皇岛： 燕山大学， 2017.

［14］ 吕丽萍. 有限元法及其在锻压工程中的应用［M］．西安： 西北工业大学出版社， 1989．

［15］ 张莉， 李升军. DEFORM在金属塑性成型中的应用［M］. 北京： 机械工业出版社， 2009.

［16］ 陈学文， 陈军， 左四雨， 等. 基于有限元分析的锻造工艺优化技术研究现状与趋势［J］. 锻压装备与制造技术， 2004， 39： 14.

［17］ 严巍， 陈国学. 轴对称压缩流动应力-应变曲线有限元修正方法的研究［J］. 塑性工程学报， 2004， 11： 19.

［18］ Ebrahimi R， Najafizadeh A. A new method for evaluation of friction in bulk metal forming ［J］. J Mater Process Tech， 2004， 152： 136.

［19］ 彭大暑. 金属塑性加工原理［M］. 长沙： 中南大学出版社， 2004.

［20］ Hamouda A M S. Effect of energy losses during an impact event on the dynamic flow stress ［J］. J Mater Process Tech， 2002， 124： 209.

［21］  Li L， Zhou J， Duszczyk J. Determination of a constitutive relationship for AZ31B magnesium and validation through comparison between simulated and real extrusion ［J］. J Mater Process Tech， 2006， 172： 372.

［22］ Goetz R L， Semiatin S L. The adiabatic correction factor for deformation heating during the uniaxial compression test ［J］. J Mater Eng Perform， 2001， 10： 710.

［23］ Sellars C M， Mctegart W J. On the mechanism of hot deformation ［J］. Acta Metallurgica， 1966， 14： 1136.

［24］ Zener C， Hollomon J H. Effect of strain rate upon the plastic flow of steel ［J］. J Appl Phys， 1944， 15： 22.