基于稳像的星敏感器动态精度提升方法研究

张腾飞, 程会艳, 孟小迪, 齐静雅, 张 颖, 刘 欣

北京控制工程研究所, 北京 100094

0 引 言

星敏感器是以恒星为观测对象的姿态测量敏感仪器[1],具有精度高、无漂移和可靠性高等优点,已成为航天器实现高精度定姿定位的关键姿态测量部件[2].近年来,航天技术及光电探测技术的快速发展带动着星敏感器技术水平快速提升.复杂多样的空间任务也对星敏感器提出越来越高的要求,其中高敏捷机动、临近空间等应用场景需要星敏感器在高动态工况下实现高精度姿态测量[3].近年来国内外针对高动态工况需求开发了多款星敏感器[4-9].

星敏感器处于高动态工况时,积分时间内星点目标在星敏感器像面成像位置会发生较大变化,星点能量将分散在像面相对目标运动的轨迹上,这种现象就是拖尾.星点能量的分散降低信噪比,影响星点亚像元定心精度,使得星敏感器姿态测量精度变差,严重情况下甚至导致星敏感器无法完成姿态输出与跟踪[10].

解决动态下星敏感器精度提升有两大类方法.第一类方法是在成像时尽量减弱、消除拖尾.美国 Lockheed Martin 的 AST-301使用自主式延时积分(TDI)完成X轴向的图像运动补偿[11],但该方法仅能完成一个方向拖尾的消除.在空间望远镜应用中,HUBBLE、JWST、ATLAST-8m和ATLAST-9.2m均采用复杂的稳像系统来解决空间振动、姿态变化等原因引起的望远镜像质下降问题[12],受限于体积、功耗等因素,针对望远镜应用的稳像系统难以集成在星敏感器中.文献[13]中提出了一种基于快速反射镜的星敏感器图像稳像系统,该系统依靠星点开窗获得星点相对于图像中心的脱靶量,使用音圈电机带动快速倾斜镜反向位移补偿,适用于观测单颗星的星敏感器.另一大类方法是在拖尾产生后,使用算法尽可能提升星点信噪比和产品精度.可以将运动拖尾现象作为图像退化,使用传统图像复原技术处理[14-18],这类方法可以消除运动拖尾,但噪声的影响导致图像复原对精度提升有限,并且图像复原涉及的复杂运算占用较大的时间和资源限制其实时应用.文献[19]提出来利用陀螺提供的姿态角速度信息计算星点轨迹并利用星点能量分布公式得到拖尾星图和灰度加权中心,并与实际星图灰度加权中心进行反复修正迭代,该方法可以提升振动环境下星点定心精度,但复杂的迭代修正运算限制了算法的实时应用.文献[20]提出了使用多帧星图重构后叠加来提升信噪比的方法,有一定的效果,但限制了姿态更新率的提升.

本文提出一种基于稳像的星敏感器动态精度提升方法,利用陀螺实时获取角速度,在星敏感器曝光期间,使用像面驱动器驱动成像芯片补偿运动实现稳像,减小甚至消除拖尾,提升产品信噪比和精度.本文将对该稳像方法进行详述,并搭建验证系统对该方法进行评估.

1 星敏感器运动拖尾模型

按照星点目标和星敏感器像面的相对运动来区分,星敏感器在轨运动可以分为像面相对星点平动以及星敏感器绕其3个坐标轴旋转.基于星点目标的距离因素,像面相对星点的平动几乎不会对成像结果产生影响.接下来需要对星敏感器绕其三轴转动进行分析.

由于星敏感器积分时间Δt较为短暂,一般可以认为积分过程中星敏感器绕其三轴的运动速度为常值,分别为ωx、ωy、ωz.首先对星敏感器绕其X轴的运动进行分析,如图1所示.

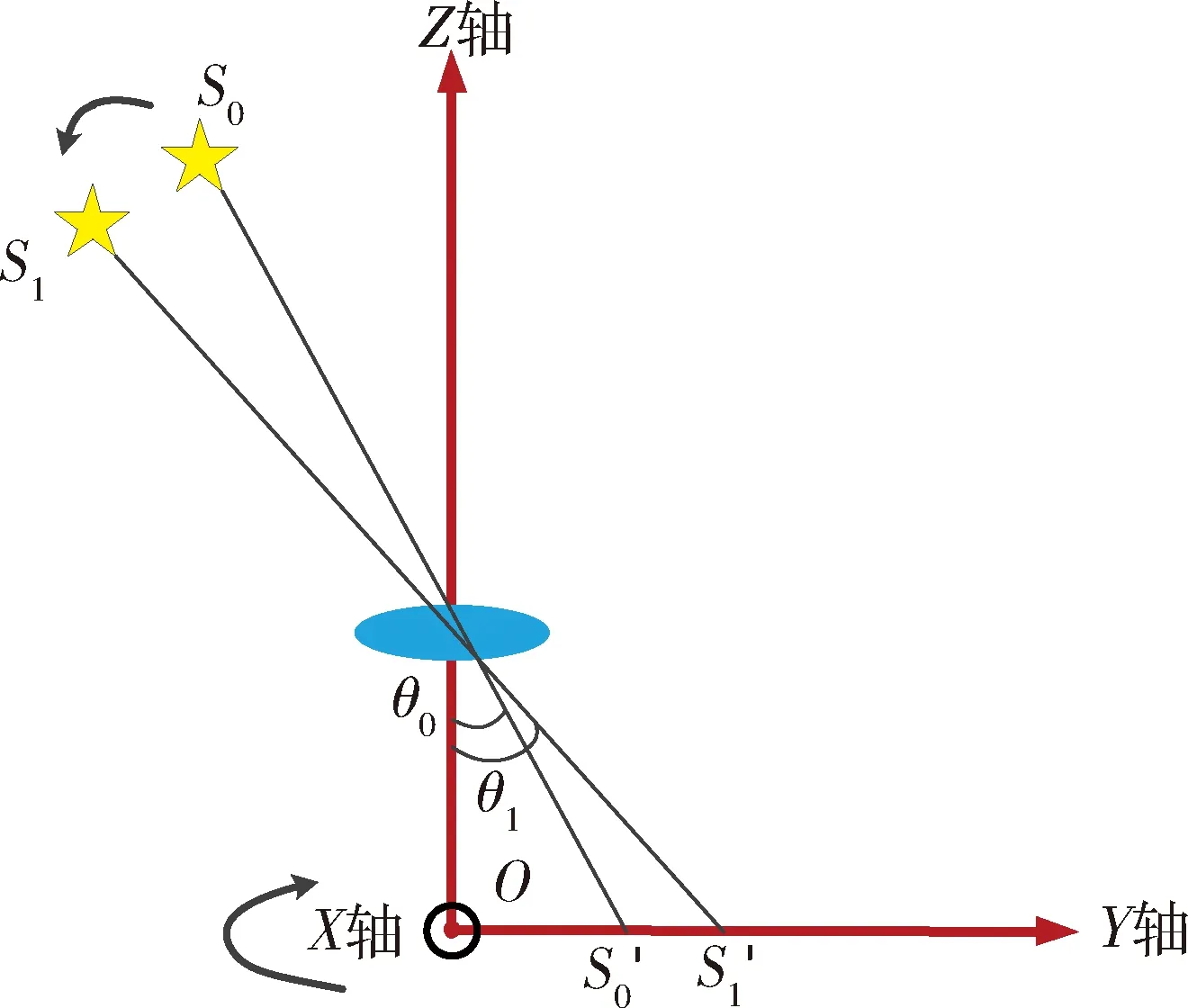
图1 星敏感器绕X轴运动示意

图1中星敏感器X轴垂直于纸面向外,Y轴向右,Z轴也是星敏感器的光轴,方向朝上.星点S0与光轴的夹角为θ0,在像面的成像位置为S′0.积分时间内星敏感器绕其X轴做角速度为ωx的匀速运动,过程中星点与光轴的夹角由θ0变为θ1,星点在像面的成像位置由S′0变为S′1,星点在像面成像位置的变化即为拖尾长度,如式(1)所示.

Ly=f(tan(θ1)-tan(θ0))/d

(1)

式中,Ly为拖尾长度,单位(pixel),f为星敏感器焦距,d为像元的尺寸,由于θ1和θ0均很小,式(1)可简化为

Ly≈f(θ1-θ0)/d=fΔθ/d=fωxΔt/d

(2)

同理,星敏感器绕其Y轴运动在积分时间内的拖尾长度为

Lx≈fωyΔt/d

(3)

星敏感器绕其Z轴旋转时产生的拖尾和绕X、Y轴旋转时不一致,如图2所示.

图2 星敏感器绕Z轴运动示意

由图2可知,星敏感器绕其Z轴旋转在积分时间的拖尾长度为

Lz≈RωzΔt/d

(4)

式中,Lz为拖尾长度,单位(pixel),R为星点在像面成像位置与像面中心的距离.与公式(2)、(3)比较,绕X、Y轴旋转时拖尾长度与星敏感器焦距成正比例,而绕Z轴旋转时拖尾长度与星点成像位置距离像面中心的距离成正比例,由于像面大小与星敏感器焦距一般相差十倍以上,在相同角速度下绕Z轴旋转产生的拖尾很小,一般可忽略.

当星敏感器同时存在绕X轴、Y轴的旋转时,将两种运动产生的拖尾合成后如下所示:

(5)

角速度合成后如下所示:

(6)

因此星敏感器同时存在绕X轴、Y轴的旋转时产生的拖尾方向与X轴、Y轴成一定的夹角,如图3所示.

图3 星敏感器绕X、Y轴旋转产生拖尾示意

2 稳像方法

2.1 稳像系统设计

除了星敏感器常规的组件外,增加了陀螺和像面驱动器组件.当星敏感器随平台运动时,陀螺可实时获取其运动角速度信息,通过地面提前标定好的陀螺坐标系与星敏感器像面坐标系O-XY的转换关系,将测得的陀螺运动角速度转换为像面坐标系O-XY的运动角速度:ωx、ωy,根据式(6)合成像面角速度ωxy,可求得像面坐标系的运动速度

Vxy=ωxy×f

(7)

在星敏感器曝光期间,二维像面驱动器可带动图像探测器以相反的速度-Vxy运动,补偿图像探测器(即像面)相对于探测目标的运动,从而减小甚至消除成像中的拖尾.

2.2 稳像系统实现

在稳像系统中使用高性能硅基MEMS陀螺采集运动角速度,它具有重量轻、启动时间短、零偏稳定性高、采样率高等优点.

在稳像系统中需使用的像面驱动器有音圈电机和压电陶瓷两种.其中音圈电机是一种将电信号转换为直线位移的直流电机.压电陶瓷驱动器是利用电介质在电场中的逆压电效应或电致伸缩效应将电能转换成机械能,产生微位移的换能元件.同音圈驱动器相比,压电陶瓷驱动器不发热,控制方式简单,目前大多数的空间激光通信系统的精跟踪和提前量伺服机构都为压电陶瓷.因此稳像系统中使用二维压电陶瓷像面驱动器来驱动成像芯片补偿运动.

3 稳像技术验证方法

为了验证星敏感器稳像系统,搭建了一套地面验证系统,利用单星模拟器模拟空间星点目标,将集成了稳像系统的星敏感器安装在转台上,控制转台带动产品运动来模拟在轨平台运动,如图4所示.

图4 星敏感器稳像验证系统

验证系统中的星敏感器瞬时视场角约为16″/pixel,以角速度0.6(°)/s为例,计算可得100 ms积分时间星点的拖尾长度约为13个像元.图5分别为星敏感器静态下星点成像结果、0.6(°)/s工况下未经稳像的星点成像结果以及在0.6(°)/s工况下经稳像系统补偿后的星点成像结果.

由图5中可以看出动态工况下经稳像系统补偿后的星点成像结果中几乎没有拖尾,与静态工况下星点成像结果近似,接近于标准的点扩散函数模型,下文中将具体介绍对稳像技术的验证过程、方法和结果.

图5 星敏感器静态、动态未稳像、动态稳像后星图

3.1 星图采集方式

分别在使能稳像和不使能稳像情况下利用转台带动星敏感器以图中所示对角线为轴进行0.6(°)/s的匀速旋转,转台运动时星点沿着与转动轴向垂直的方向依次成像,对上述运动及星图采集过程进行20次重复操作.为了比较动态和静态工况下不同视场位置的定心精度,从动态成像采样位置中选取图中所示的7个位置,使得星点分别静止在这7个位置连续采集20幅静态星图,如图6所示.

图6 星敏感器运动及采样示意

3.2 评价方法

(1)星点高斯半径及星点能量峰值

理想情况下,静态时星敏感器恒星目标在星敏感器像面上形成一个无限小的光点,此时星点定心结果会受限于像元尺寸.因此星敏感器通常采用适当的离焦处理,使得星点成像后不是一个无限小的光点,而是一小片的光斑,再利用质心法等方法实现星点质心坐标的亚像素提取,突破了像元的限制.

适当离焦后,星点能量在星敏感器像面的灰度分布接近二维高斯正态分布,如下所示:

(8)

其中,(x,y)为像面不同位置,E(x,y)为像面不同位置的灰度,(x0,y0)为星点成像质心,E0为像面接收到总能量对应的灰度值,σ为高斯半径,高斯半径取决于星敏感器离焦程度.

动态工况下,星点成像位置在不断变化,此时星点能量在像面的灰度分布如下所示:

E(x,y)=

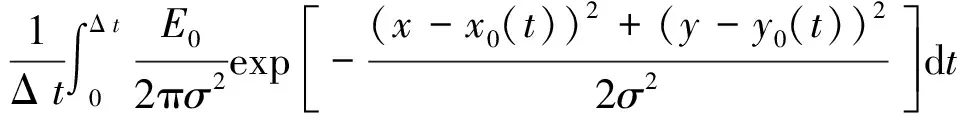
(9)

其中,(x0(t),y0(t))为随时间变化的星点像元中心坐标,Δt为积分时间.星点能量在像面的分布与速度、积分时间2个参数相关.速度越大、积分时间越长,像元中心坐标变化幅度越大,星点拖尾就越长.

由于动态工况会导致星点能量分散在更大的面积上,对星点动态成像结果进行二维高斯拟合后,相比静态时高斯半径会变大.稳像补偿后星点能量汇聚,高斯半径相对未稳像减小.可以对不同工况下的星点成像结果进行二维高斯拟合,利用高斯半径评价稳像效果.

星点能量峰值是对成像星图进行星点提取后得到的星点所有像元的最大灰度值,动态工况下星点成像位置不断变化,星点像面中心能量被分散在运动方向上,导致星点能量峰值减小.稳像补偿后星点成像位置变化减小,星点峰值能量会变高.可以在不同工况下对星点峰值能量进行分析,评价稳像效果.

(2)星点定心精度

对提取星点利用质心法得到亚像素坐标结果,星点坐标的不确定性即为星点定心精度,决定了星敏感器姿态测量精度.动态工况会导致星点能量分散在更大的面积上,降低信噪比,导致星点亚像元定心精度变差.稳像补偿后星点能量汇聚,信噪比增大,星点定心精度相比未稳像时变好.

计算多次采样的星点定心坐标的标准差stdx、stdy,该结果即可视作星点定心精度,对不同工况下星点成像定心精度进行分析,评价稳像效果.

(3)相关系数

相关系数是指2个大小相同样本的相关性,范围在-1～1之间,表示2个样本之间线性关系的强度和方向.当2个图像相似度较高时,相关系数的计算结果应接近1.动态情况下星点灰度分布如公式所示,与静态下分布相关性减小,相关系数也会变小.稳像补偿后更接近公式所示的静态成像模型,相比稳像前,与静态图像相关系数变大.可以对不同工况星图间的相关系数分析来评价稳像效果.

4 稳像技术验证结果

4.1 星点定心精度

对3.1节中描述的在静态下、动态稳像补偿、动态未稳像工况采集的20次星点定心结果进行统计得到星点坐标标准差stdx、stdy.此外利用陀螺测得的角速度信息结合文献[20]提到的方法,对多帧星图重构后叠加,再进行星点质心坐标提取并统计坐标标准差.结果如图7所示.

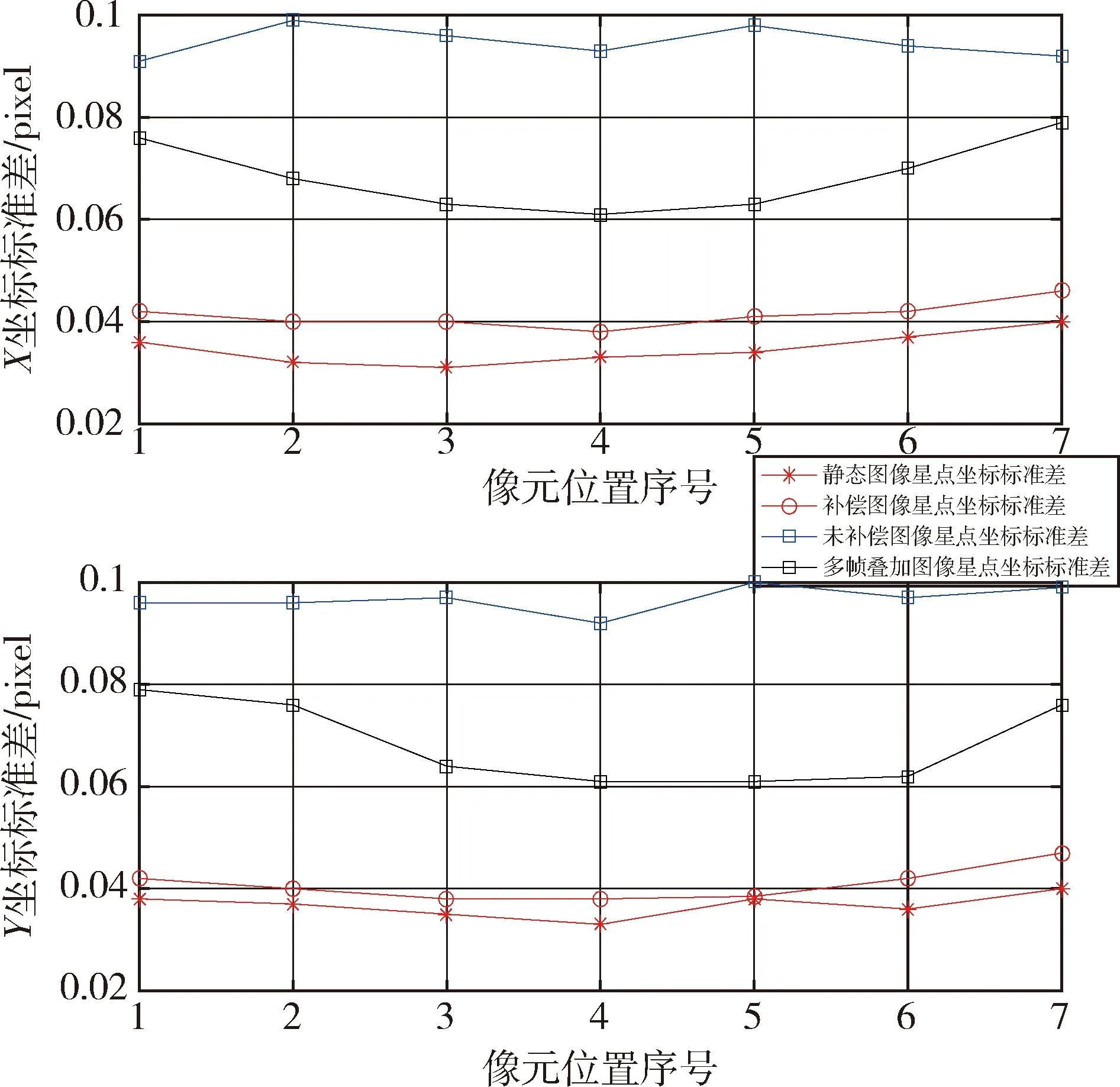
图7 不同工况对定心精度影响

由图7可知:对动态多帧星图重构叠加后定心精度提升了约26.8%.而动态稳像补偿后产品定心精度相比动态未稳像提升了约57.2%,已接近静态定心精度,说明稳像系统行之有效,效果明显优于多帧叠加算法对精度的提升.

4.2 星点高斯半径、星点能量峰值

3种工况下高斯半径如图8所示.

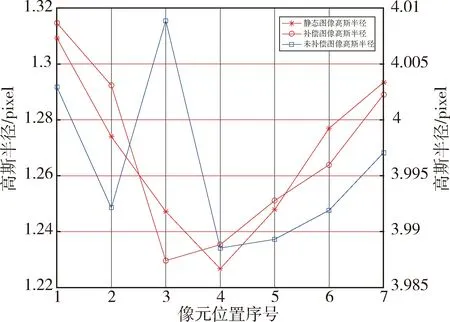
图8 不同工况对高斯半径的影响

由图8可知:稳像补偿后星图高斯半径与静态下星图高斯半径非常接近,相对偏差分布在0.005～0.02之间.未稳像补偿图像的高斯半径是稳像补偿后图像的3倍以上,说明稳像系统运作良好.

3种工况的能量峰值如图9所示.

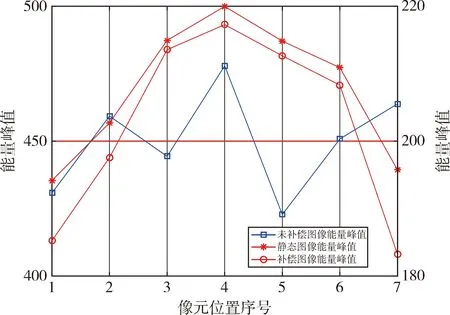
图9 不同工况对能量峰值的影响

从图9可知:稳像补偿后的图像的能量峰值略低于静态图像,相对偏差分布在0.02～0.066之间,稳像补偿后图像的能量峰值是未稳像补偿图像的2倍以上.

4.3 相关性分析

基于相关系数的理论计算图像之间的相关性,比较得到稳像补偿后图像和静态图像之间、未经稳像补偿的图像和静态图像之间、静态图像之间相似程度如图10所示.

从图10中图像相关性结果分析可知:静态图像之间的相关性基本上大于0.995;补偿图像与静态图像之间的相关系数分布在0.975～0.99范围内,表明补偿后图像与静态图像相似度极高;未补偿图像和静态图像之间相关系数分布在0.668～0.678范围内.

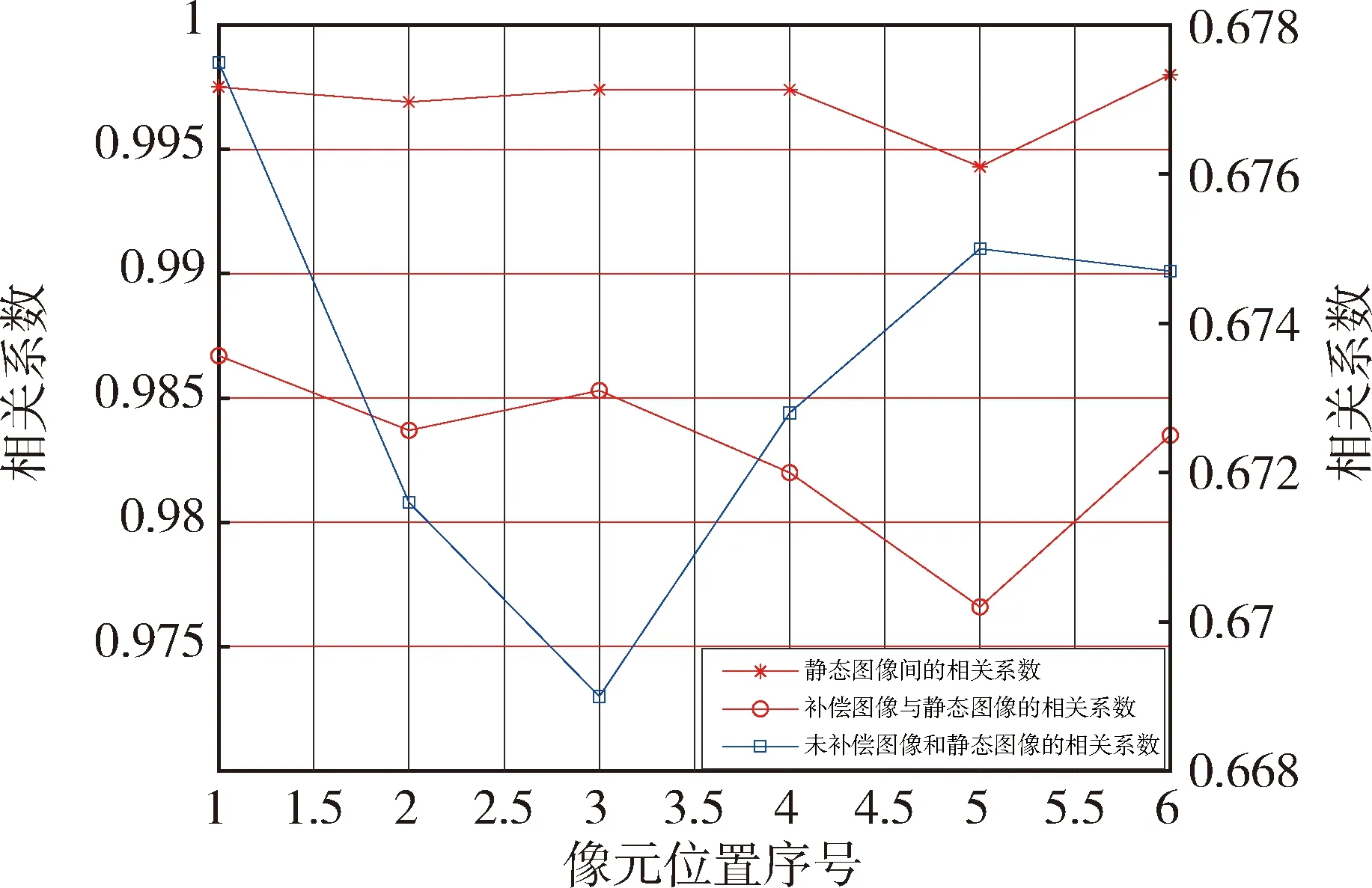
图10 不同工况对图像间相关系数的影响

4.4 验证结果分析

从星点定心精度、高斯半径、峰值能量和相关系数等多项指标评估,动态工况下稳像补偿后相对未稳像补偿,各项指标均有大幅改善,接近静态工况下技术指标.此外从定心精度分析结果可知,使用稳像方法效果明显优于使用多帧叠加算法,这也说明了提前消除拖尾方法相比后期算法的天然优势.

但动态工况下稳像补偿后各项指标相比静态工况还存在一定差距,对稳像技术的具体实现分析可知,陀螺测速误差、像面驱动器定位误差以及稳像补偿式(7)简化时的误差,是影响稳像补偿效果的因素.

5 结 论

本文针对高动态工况下星敏感器拖尾导致精度下降的问题,设计了一种基于陀螺和像面驱动器的稳像技术,试验验证表明稳像补偿后星点定心精度、高斯半径、能量峰值、相关系数等多项指标均有大幅提升,该稳像补偿方法相对多帧叠加算法在提升定心精度方面也有明显优势.本文提出的稳像技术可广泛应用于具有动态应用场景的星敏感器及其他光电成像仪器中.