基于深度强化学习的航天器多约束规避动作快速规划

吴健发, 魏春岭*, 张海博, 李克行, 郝仁剑

1.北京控制工程研究所, 北京 100094 2.空间智能控制技术全国重点实验室, 北京 100094

0 引 言

由于非合作航天器和空间碎片的数量激增,导致近期轨道危险交会事件频发,对我国航天器的在轨安全运行造成严重威胁.例如2021年7月1日和10月21日,“星链”卫星两次接近我国空间站,迫使我空间站进行主动规避.面对日益拥挤的轨道空间环境,研究航天器自主规避动作规划技术已成为众多学者的共识[1],近来涌现出大量具有启发性的学术成果[2-12].然而根据调研,上述研究中提出的规避动作规划方法普遍存在无法生成更为精细的姿轨机动动作指令或快速反应能力不足的问题,难以完全适应多约束、近距离条件下的航天器复杂规避情景,具体体现在以下方面:

1)所建立的决策规划模型多基于比较简单的三自由度C-W轨道运动方程或二体运动方程,在规划时仅考虑了航天器的位置、轨控加速度和能量等简单约束条件[2-7].这虽然可以降低规划求解的难度,但却无法进一步描述规避机动过程中面临的多种复杂非线性的姿态指向、输入有界和安全性约束条件[8-13].例如,星敏感器和通信天线的正常工作需要航天器满足一定的姿态指向约束;姿控力矩和姿态角速度存在有界约束;近距离交会时还须建立航天器外形与轨道威胁间的精细化碰撞约束等.可能导致据此规划出的轨迹与实际飞行轨迹间存在较大偏差,或难以完全满足航天器的稳定运行需求.

2)对于上述问题,一些研究提出在建立复杂模型的基础上,采用高斯伪谱[8-10]、模型预测控制[11-12]等数值优化方法实现航天器多约束规避动作在线规划,其在航天器远距离威胁规避或近距离低速交会对接情景下具有较好的规划效果.然而在实际中,星载探测设备存在一定的漏检率,当再次检测到威胁时,双方预期交会时间可能仅有数十秒,而文献[8-12]的数值优化方法往往存在初值敏感、求解效率低、计算时间长等问题[14],难以满足相应的高频率实时规划需求.

近年来,以深度强化学习为代表的新一代人工智能技术蓬勃发展,为上述问题的解决带来希望[15]:一方面,深度强化学习所引入的深度神经网络具有强大的非线性逼近能力,能在与环境的交互训练中通过反馈的奖励信号充分提取环境中的约束特征继而学习到受限条件的状态转移规律,目前已在复杂地形下的无人机机动控制[16]、再入飞行器姿态控制[17]、航天器碎片规避轨道控制[18]等典型多约束优化控制问题中得到应用;另一方面,训练成型的深度神经网络在线应用时只需进行前向传播,没有复杂的数值计算过程,适用于具有高实时性需求的决策任务.鉴于此,本文围绕航天器规避机动任务需求,提出一种基于深度强化学习的航天器规避动作规划方法,可在航天器姿态指向变化较小的前提下快速生成满足多种复杂约束的姿轨规避动作,并构造与规划方法相适配的深度强化学习规范化训练环境,确保学习训练过程中智能体和环境的有效交互.

1 问题描述

1.1 航天器六自由度非线性动力学建模

以刚体航天器为研究对象,假设航天器轨道为近圆轨道,主推力器安装在航天器质心,指向本体系-xb轴.以航天器探测到轨道威胁时的初始状态为参考航天器的初始状态,在VVLH坐标系下建立航天器姿轨动力学模型,如下所示:

(1)

(2)

COB=

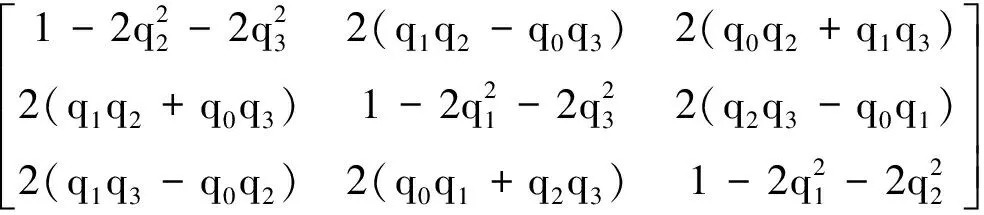
(3)

(4)

其中:式(1a)和(1b-c)分别为轨道动力学方程和姿态动力学方程;R=[xyz]T为航天器相对参考航天器的位置;n为参考航天器的轨道角速度;q=[q0q1q2q3]T为姿态四元数;ω=[ωxωyωz]T为本体系下的姿态角速度;FB=[F0 0]T和τc=[MxMyMz]T作为航天器姿轨机动的控制输入,分别为本体系下的推力和姿控力矩矢量;m为航天器质量,由于规避过程时间较短,可假设质量恒定;COB为本体系到VVLH坐标系的转换矩阵;J为转动惯量矩阵;ω×表示ω的反对称矩阵.

1.2 约束条件

1)状态/输入有界约束

航天器的姿态角速度和控制输入需满足相应的有界约束条件,如下所示:

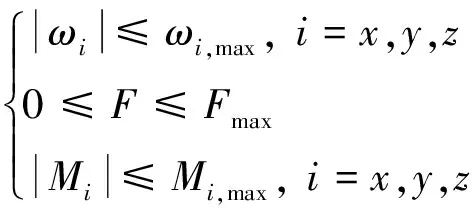
(5)

2)姿态指向约束

航天器装备有多种光学敏感器,其在姿轨机动过程中必须避免太阳等光源进入敏感器视场,即光源方向矢量和敏感器的视线轴方向夹角不低于敏感器安全视场角,以保证敏感器的正常工作,因此需对航天器的姿态指向进行限制,如下所示:

(6)

式(6)中,rB,i和σi分别为敏感器i在本体系下的指向和安全视场角,rO为光源在LLVH坐标系下的指向.

此外,应尽量以较小的姿态指向变化完成规避机动,以确保对地天线、相机等任务载荷的业务连续性,可建模为如下软约束JP:

|ψ(t′)-ψ0|)dt

(7)

式(7)中:φ、θ、ψ分别为航天器的滚动角、俯仰角和偏航角,其值可由四元数解算;φ0、θ0、ψ0为初始姿态角;机动过程中JP越小,规避动作质量越高;姿态角变化|φ-φ0|、|θ-θ0|、|ψ-ψ0|在计算时需考虑俯仰角在±90°时以及滚动角和偏航角在±180°时的不连续变化问题.

3)考虑航天器外形的精细化碰撞约束

近距离危险交会时,由于航天器除主体结构外一般还安装有太阳帆板或天线等附属结构,如果简单将航天器的碰撞约束建模为规则形状包络,例如球体、椭球体及其组合体,则会严重压缩航天器的姿轨规避机动空间,导致动作规划方法难以计算可行解,因此还需要结合航天器的实际外形,构建精细化的碰撞约束.具体来说,首先将威胁视为球体,其位置为RT,安全半径为LT,然后以航天器的质心为基准点,以d为间距,将其外形离散化为N个坐标点,各点在本体系下相对于基准点的坐标为rS,i(i=1,2,…,N),则碰撞约束定义如下:

(8)

1.3 规避成功的判定条件

在航天器始终满足上述约束条件的前提下,当航天器处于威胁后半球(航天器相对于威胁的位置矢量与威胁速度矢量的夹角大于90°时的区域),且双方相距大于距离阈值LS时,可判定航天器规避成功,该条件可建模为

∃t′,

s.t.

(∀t∈[0,t′],s.t.式(5-6,8))∩

(9)

式(9)中,〈·,·〉表示矢量夹角.

2 动作规划方法设计

2.1 深度强化学习训练算法

强化学习的基本要素包括智能体(由策略和训练算法组成)和训练环境,其中,训练环境通过奖励函数评估智能体的行为并给予相应的激励信号,而智能体则根据环境反馈输出动作影响环境状态.在双方“试错”的过程中,智能体通过训练算法不断更新其策略,以尽可能地获得更高的长期奖励.深度强化学习则是上述概念基础上,以深度神经网络作为智能体策略的表现形式,并辅之以配套的训练算法.考虑到航天器规避动作规划问题具有连续状态/动作属性,并结合作者及其合作者近年来在再入飞行器姿态控制和航天器轨道机动控制等复杂多约束动力系统控制问题[17-18]中的实践经验,本文采用双延迟深度确定性策略梯度(twin delayed deep deterministic policy gradient, TD3)算法[19]作为深度强化学习的训练算法,该算法是在深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法基础上的一个改进[20],是目前最先进的面向连续控制的深度强化学习算法之一.DDPG基于“动作-评价”机制,利用深度神经网络逼近价值函数和确定性策略.由于价值函数逼近过程中常出现价值过估计现象,恶化训练效果,因此FUJIMOTO等在DDPG的基础上进一步使用两套评价网络来估计值函数,并且使用动作网络延迟更新和目标动作网络平滑正则化等操作来进一步提高算法的收敛性.

TD3中共计使用了1个动作现实网络、1个动作目标网络、2个评价现实网络以及2个评价目标网络.算法和神经网络的结构分别如图1～2所示.动作网络的输入为环境反馈的观测量o,由输入层、全连接层、线性整流单元层和双曲正切层组成.评价网络的输入则包括观测量o和动作量a,由输入层、全连接层、线性整流单元层和叠加层组成.

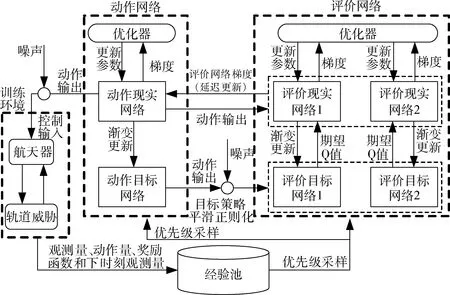
图1 TD3深度强化学习算法

结合前面所述的航天器规避机动模型与约束条件,首先构造o和a.

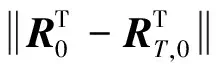
(10)

对于a,文献[21-22]的思路是直接将其定义为控制输入,如式(11)所示(进行了相应归一化处理),这样可直接对控制输入进行有界约束,但却无法约束规避过程中的角速率,必须在奖励函数中额外设置复杂的状态有界项,进行更加充分的训练.为使智能体在训练中尽可能生成满足状态有界约束的控制输入,从而降低训练的难度,本文首先基于式(1c)和动态逆方法[23]设计一个角速率控制器,如式(12)所示,以此为基础,将a定义归一化推力F和指令角速率ωc=[ωx,cωy,cωz,c]T的组合,如式(13)所示,从而实现对角速率的直接限幅

(11)

τc=sat(J·(K(ωc-ω)+J-1ω×Jω))

(12)

(13)

在此基础上,基于TD3深度强化学习算法训练智能体,具体算法流程和相关参数解释如文献[19]所示.

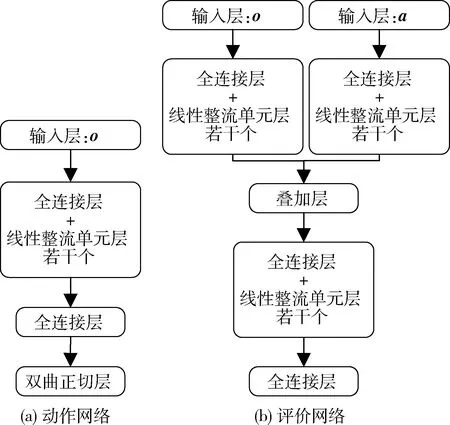
图2 动作网络和评价网络

2.2 在线应用

如图3所示,训练结束后,从智能体中提取动作网络用于实际环境下的在线重规划,给定神经网络相应的观测量即可快速生成相应规避机动动作.

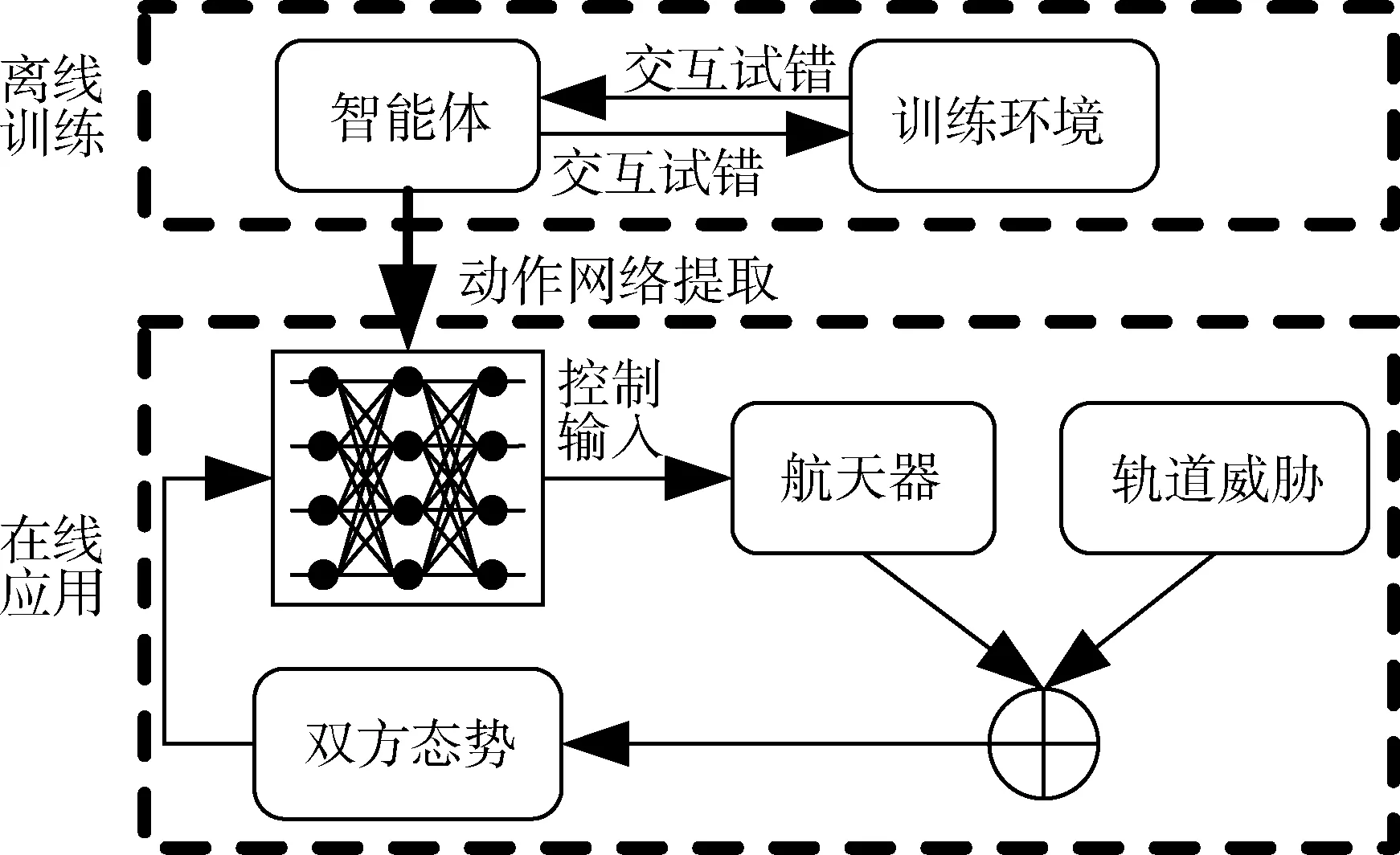
图3 深度强化学习算法的在线应用

2.3 规范化训练环境建模

训练环境对深度强化学习算法的训练效能影响巨大,如果设置不当,可能会在训练中出现即使航天器不机动也不会与威胁发生交会的无效交互情况,因此有必要对训练环境进行合理设计.本文围绕多约束规避机动任务需求,提出具有规范化设计步骤的训练环境建模方法,主要包括以下3部分内容:初始状态设置、训练环境重置条件设计以及奖励函数设计.

(1)初始状态设置

然后,设定航天器自探测到威胁至双方发生预期交会的时间tR.在此基础上,定义并随机初始化威胁相对航天器的速度幅值ΔV∈[ΔVmin,ΔVmax]、方位夹角α∈[-π,π]和β∈[-0.5π,0.5π],则轨道威胁的位置方程设定如下所示:

RT(t)=(tR-t)ΔV[cosαcosβsinαcosβsinβ]T

(14)

基于上述轨道威胁初始状态设置方法,可确保在训练过程中如果航天器不进行规避机动,则必然与威胁发生交会.

(2)训练环境重置条件设计

环境重置条件设置为航天器部件与威胁发生碰撞或规避成功,即不满足式(8)或满足式(9).

(3)奖励函数设计

奖励函数r设计如下:

(15)

rP=-|φ-φ0|-|θ-θ0|-|ψ-ψ0|

(16)

其中,rP和wP分别为基于式(7)指标构造的姿态指向奖励项及其权重,re,1<0和re,2>0分别为规避失败和成功时的恒定惩罚和奖励值.r的目的是鼓励以较小的姿态指向变化(即JP)完成多约束规避机动.

3 仿真分析

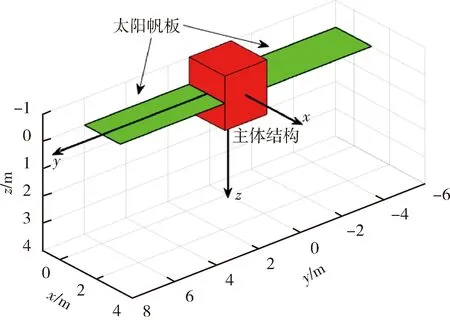
图4 本文中航天器的外形

轨道威胁参数设置为: 预期交会时间为tR=20 s;相对方位和速度参数为α=-30°、β=-25°和ΔV=30 m/s;安全半径为LT=2 m.

TD3参数设置为:动作规划采样步长为0.1 s;训练回合数为100 000;回合最大迭代次数为250;评价网络和动作网络的学习率均为0.000 1;批大小为S=512,折扣因子为η=0.99;渐变更新系数为τ=0.005;噪声方差为0.05,更新周期为D=5.神经网络参数设置为:动作网络中,“全连接层(FC)+线性整流单元层(ReLU)”(下面简称“FC+ReLU”)组合共有3个;评价网络中,叠加层之前两条通路各有2个“FC+ReLU”组合,叠加层之后拥有1个“FC+ReLU”组合;两种网络中,全连接层的节点数均为128.

仿真中共有2个对比项:对比项1为仅以最大推力进行轨道机动的规避方式;对比项2为基于高斯伪谱法的规避动作离线规划方法,其目标函数设置为式(7),路径约束设置为式(6)和式(8).仿真计算机配置为CPU AMD Ryzen 7-5800 3.40 GHz, RAM 16 GB.仿真软件环境为Matlab 2021a, 对比项2采用GPOPS-II高斯伪谱工具包进行验证.

TD3训练过程中的平均奖励函数曲线如图5所示, 其于80 000回合后能够进入收敛状态, 表明智能体与所构建的规范化训练环境间能够进行有效交互.在此基础上进一步验证所提方法, 则临近交会时航天器与威胁的最近距离如图6所示, 航天器的姿态角、角速度、推力、姿控力矩和姿态指向约束情况分别如图7～11所示, 规划算法的运行时间如表1所示.

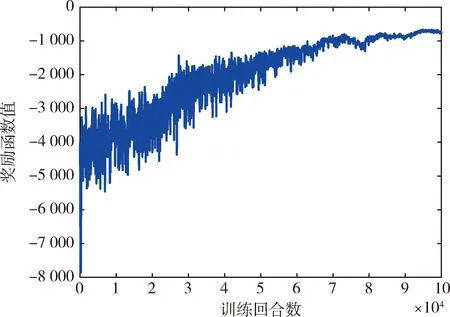
图5 TD3训练过程中的平均奖励函数曲线

图6 预期交会时间附近航天器与威胁的最近距离

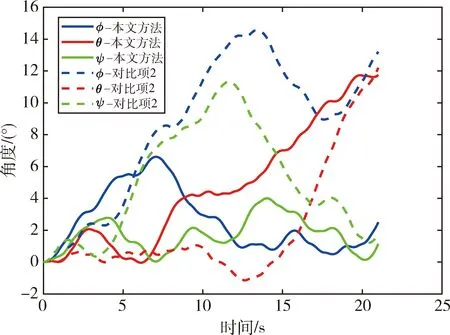
图7 航天器的姿态角

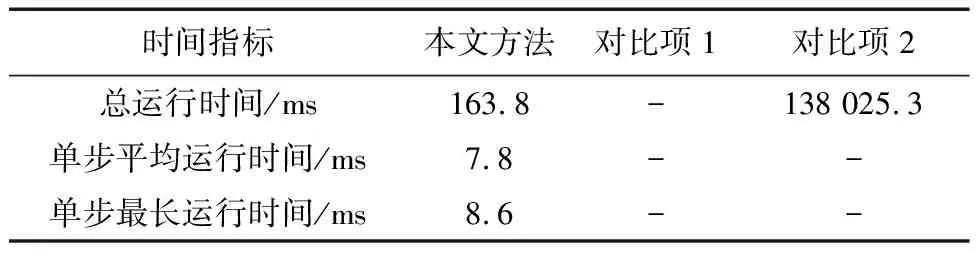
表1 规划算法的运行时间

结果可见, 如果航天器仅以最大推力进行轨道机动, 而并不调整姿态, 则其外形结构将与威胁发生交会, 而在此基础上基于本文方法和高斯伪谱法进一步规划相应姿态, 都能使航天器在满足多种复杂约束条件的前提下(如图8～11所示), 以较小的姿态变化(最大变化不超过12°, 如图7所示)实现安全规避.相较于传统的高斯伪谱规划方法, 同仿真平台下本文方法的总运行时间仅有其0.12%, 且单步运行时间不超过9 ms, 能够实现规避动作的实时规划, 可将其应用于具有快速反应需求的航天器应急规避任务场景中.

图8 航天器的姿态角速度

图9 航天器的推力

图10 航天器的姿控力矩

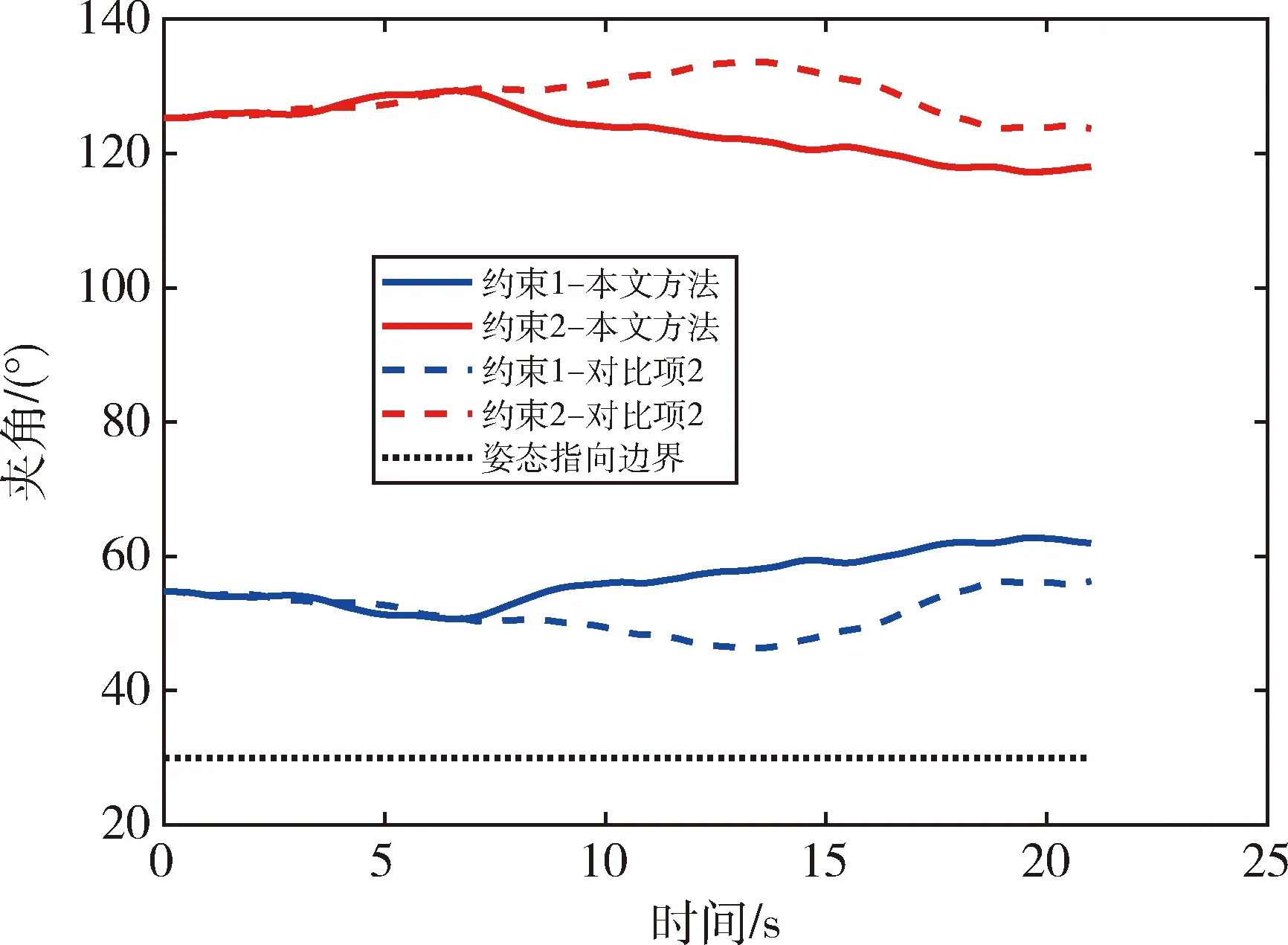
图11 姿态指向约束

4 结 论

面向航天器多约束、短时间应急规避任务情景,本文提出一种基于TD3深度强化学习算法的规避动作快速规划方法,并构造了与其相适配的深度强化学习规范化训练环境.仿真结果表明,所提方法能在预期交会时间为20 s的情况下快速实时生成满足多种复杂约束的安全规避动作,各姿态角调整不超过12°,规划周期小于9 ms,总运行时间仅为高斯伪谱法的0.12%.