大型分块式空间望远镜主镜合像/振动一体化控制方法

张祥瑞, 张 尧*, 王有懿, 毛岸远

1.北京理工大学, 北京 100081 2.北京控制工程研究所, 北京 100094

0 引 言

随着人类航天技术的进步和宇宙探索能力的提高,人类对于空间观测的需求不断提升.空间望远镜因其不受气象条件和昼夜等影响、全球覆盖、工作光谱范围大等明显优势而得到重点研究和应用[1],美国的哈勃空间望远镜[2]和我国正在研制的巡天空间望远镜[3]便是其中的代表.空间望远镜的分辨率和成像质量与望远镜口径正相关.由于传统的单一主镜空间望远镜受限于大尺寸主镜加工精度、重力变形、发射受限等问题,各国科学工作者积极推动分块式望远镜的研制.其中,分块式地基望远镜以美国的Keck望远镜[4]和我国的LAMOST[5]为代表,均在空间观测中取得优异成果.分块式空间望远镜以美国的James Webb望远镜[6]为代表,目前已发射就位并拍摄回传大量的最新观测数据,并还提出了ATLAST[7](10 m级口径)、TMST[8](30 m级口径)规划,拟在国际空间站(ISS)进行OPTIIX[9]在轨组装试验.而我国的分块式空间望远镜研究起步较晚,相关的在轨精稳装调技术的研究仍处于探索阶段且尚无成熟的应用案例,因此亟需开展分块式空间望远镜的在轨精稳拼接装调理论方法和实物试验研究,为我国下一代超大口径空间观测系统提供基础与支撑.

在分块式空间望远镜的成像过程中,主镜高精度面形控制是保证成像质量的关键,其分为子镜面形控制和子镜位姿控制[10].子镜面形控制即是通过安装在子镜面背部的若干作动器协同作用使子镜面产生变形,以调整子镜面形为理想曲面[11].在子镜面形调整完成后,各子镜位姿的高精度控制与保持是拼接形成主镜理想面形的关键,本文的研究也主要聚焦于子镜已被调整为理想面形后的整体主镜面形控制和保持问题.

在子镜面形已调整为理想面形的前提下,使用子镜背部的主动调整机构来调整子镜位姿实现理想成像.其中,首先需要建立最终像差和各子镜位姿误差间的关系以获得子镜位姿误差量作为合像调整量;其次,设计主动调整机构作为执行机构,调整子镜位姿实现合像,并进一步考虑影响子镜位姿稳定保持的星上各种执行机构产生的微振动,这要求主动调整机构具备合像/振动一体化调整能力;最后,以子镜位姿误差量为控制量,结合振动控制的需求,设计对应的合像/振动一体化控制方案驱动主动调整机构,实现分块式空间望远镜的主镜合像与保持.

像差与子镜位姿误差的光学关系建立用于调整量的解算.以詹姆斯·韦伯望远镜等为代表的项目采用了复杂的波前算法和六自由度主动调整机构控制方案以实现分块镜的合像[12].其中调整量解算的数值关系建立精细,求解精度高,但解算过程复杂,时间和计算资源消耗大;LEE等[13]利用特定类型波像差系数与失调量之前的二阶关系求解调整量,求解过程简化但需解决其对噪声的敏感问题;KIM等[14]使用Zemax等光学设计软件中类似的评价函数法和逆向优化法,通过优化求解调整量,结果精度高但无法适用于口径越来越大的系统复杂失调情况.因此,本文将设法建立计算更为便捷的位姿误差光学模型,缓解目前大口径分块式空间望远镜主镜的像差-子镜位姿误差解算复杂、适应性差的问题,为后续合像/振动一体化控制提供控制信息输入.

在获得子镜位姿误差量后,需要依赖子镜支撑背板下的主动调整机构[15]调整各子镜位姿以消除误差完成合像,且航天器上各机构产生的微振动也持续影响合像保持效果,需要采取相应措施进行振动隔离与抑制.詹姆斯·韦伯望远镜的主动调整机构采用Stewart六自由度并联平台,各作动器设计采用了步进电机配合精密机械传动结构的方案,输出位移精度达到纳米尺度[16];TMT次镜调整机构采用的也是类似的Hexapod并联平台,支腿促动器采用直流伺服电机带动谐波减速器驱动精密滚珠丝杠的传动形式[17],在提高刚度、减小间隙、降低功耗、低速下顺畅运动等方面具有很好的效果.目前的分块式空间望远镜的子镜主动调整机构均采用类似方案,其在机械传动和运动调整方面性能优异,但难以避免结构复杂、装配精度要求高和调整速度缓慢的问题.同时,航天器上的微振动主要包含太阳翼、控制力矩陀螺、线缆等产生的高低频振动,这将对成像产生不可忽视的影响,而目前以詹姆斯·韦伯为代表的分块式空间望远镜主动调整机构均不具备主动隔振能力,多设计另外的被动隔振器进行振动隔离.研究人员在哈勃望远镜的太阳翼根部使用了被动阻尼器,使其自身带有的太阳能帆板的振动得到抑制从而保证了成像的效果[18];詹姆斯·韦伯望远镜上采用了可展开塔组件作为载荷整体被动隔振设备[19],其将望远镜仪器、镜面与飞船分开,这种分离操作可以让望远镜与飞船的振动、热传导有效隔离开,但是被动隔振控制精度低、鲁棒性差,只能抑制特定频率范围内的振动,因此需要引入主动隔振机构实现更宽频率和更快衰减的微振动隔离.基于以上目前主动调整机构结构复杂的问题和分块式空间望远镜的隔振需求,本文将考虑配合音圈电机、压电陶瓷等新型微作动器设计更高精度和小体积的快速驱动单元,以此为基础结合高精度测量传感器搭建具备合像/振动一体化调整能力的主动调整机构.

最后,用于分块式空间望远镜子镜位姿调整的主动调整机构多为并联机构,需要设计匹配的控制方案驱动其合像/振动调整.而并联形式的主动调整机构具有复杂耦合的运动学、动力学和驱动单元特性,这对其控制方案的设计提出了挑战.李郴荣[20]提出了滑模变结构控制与同步误差补偿相结合的同步滑模变结构控制,对平台的控制效果进行优化,使平台在保证控制精度的同时具有较强鲁棒性.在对于已有控制系统的优化上,程媛洁[21]通过设计研究经典洗出算法.使用基于遗传算法对经典洗出算法中的滤波器参数进行优化,利用遗传算法工具搜寻滤波器最优参数;武锡铜[22]将获得的模型信息引入线性扩张状态观测器中,得到模型辅助的线性扩张状态观测器,加快了观测状态的收敛速度,取得了良好的控制效果.目前针对单一并联机构的高精高稳控制方法已经取得长足发展,但在分块式空间望远镜系统中,子镜、主动调整机构、作动器数量众多且扰动复杂,目前的控制方法在多子镜位姿调整时的实时性、稳定性和同步性都存在问题.因此,本文将在分散式控制基础上设计分块式空间望远镜系统多个主动调整机构合像/振动一体化控制方案,实现其具备一定工程应用能力的快速合像与稳定成像.

本文面向在轨组装的分块式空间望远镜主镜高精度合像与稳像调整问题,在像差-子镜位姿误差关系建立方面,采用基于Zernike多项式的光学灵敏度矩阵反演方法建立像差与子镜位姿误差的光学模型,解算便捷、扩展型强;在面向合像/振动一体化调整的主动调整机构设计方面,设计音圈电机驱动的六自由度子镜主动调整机构,提出涡流传感器阵列的位姿解算方案,建立考虑微振动源影响的分块式空间望远镜整星动力学模型;在主动调整机构的合像/振动一体化控制方面,提出在轨组装后的分块式空间望远镜合像与振动控制方法,设计带有前馈补偿与速度反馈的分散式音圈电机控制器.最终仿真结果表明该方案可实现分块式空间望远镜高精度合像与振动控制,为我国的分块式空间望远镜建造提供指导.

1 分块镜系统描述

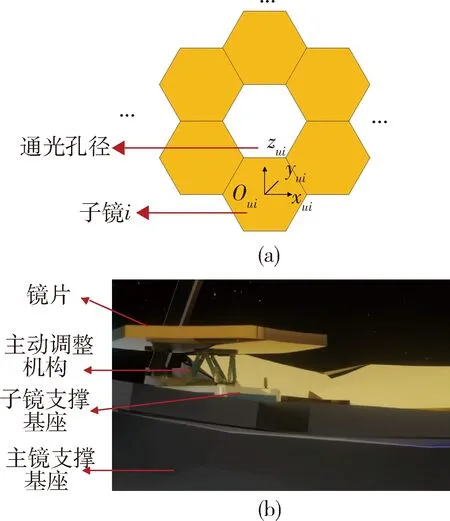
图1 分块式空间望远镜主镜镜面俯视图与主动调整机构布局

在分块式空间望远镜主镜拼接过程中,误差分为拼接误差和非拼接误差.在此假定固有的非拼接误差如镜面面形误差、重力支撑变形误差和热变形误差等均已消除,仅考虑拼接误差.建立第i个子镜上镜面坐标系为fui(Ouixuiyuizui),每个子镜均具有3个平移自由度和3个转动自由度.在所有子镜通光光轴保持一致时,由于主镜的光学对称特性,子镜在Z方向上的转动误差对成像无影响.Z方向的平移误差δz是造成波前像差主要影响项.子镜的拼接误差中,Z方向的平移误差δz和X、Y方向倾斜误差δθx、δθy是引起分块式空间望远镜波前像差的主要误差项,分别称其为Tilt、Tip和Piston误差.

2 像差与子镜位姿误差光学模型

2.1 像差描述

由于本文中的分块镜系统采用正六边形孔径,为保证Zernike多项式的正交性,使用Gram-Schmidt正交法进行六边形域内Zernike多项式求解[24].

设矩阵L=[L1…Ln]T为正六边形域Zernike多项式,矩阵Z=[Z1…Zn]T为圆域Zernike多项式,两者间有如下关系:

L=KZ

(1)

其中,n为Zernike多项式阶数,K为转换矩阵.

则基于Gram-Schmidt正交方法的六边形域内正交化迭代公式如下:

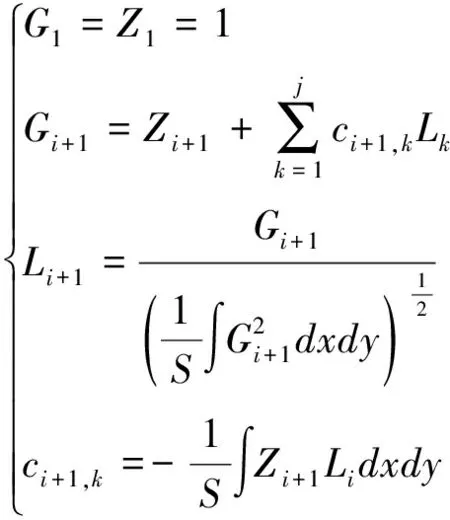
(2)

迭代正交化后的正六边形域Zernike多项式前9项如表1所示。

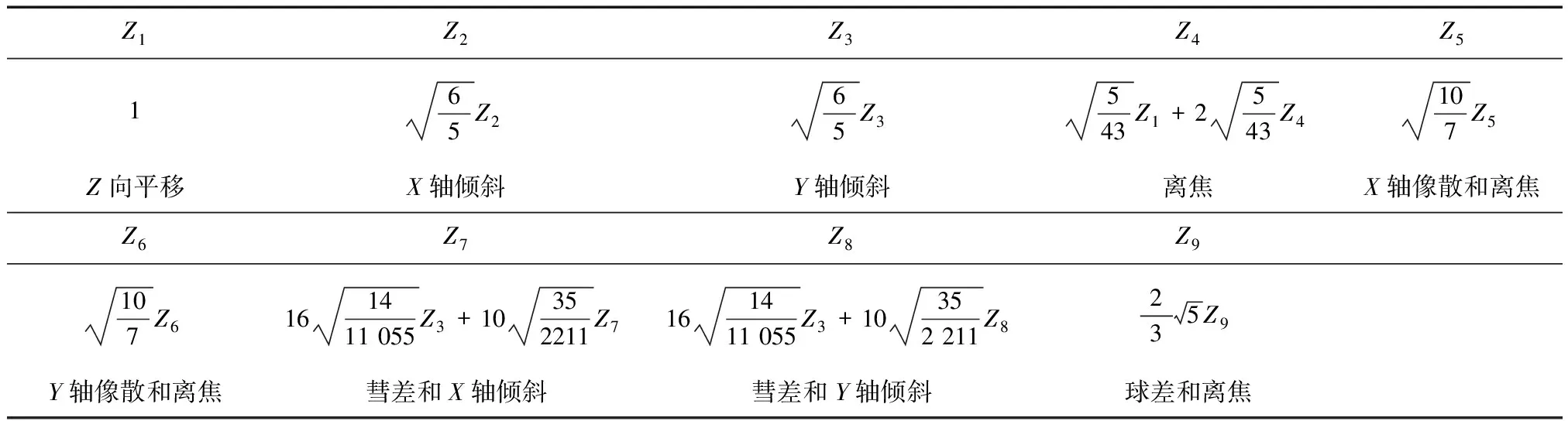
表1 正六边形域Zernike多项式

2.2 像差与子镜位姿误差关系

在一定范围内,可以认为分块式空间望远镜像差与子镜位姿误差为线性关系,建立像差与子镜位姿误差间的灵敏度矩阵关系式

ΔL=AΔX

(3)

其中,ΔL为像差变化量,本文中为Zernike多项式变化量,实际使用中由波前传感器等测得;A为灵敏度矩阵,ΔX为子镜位姿误差.在近似线性的条件下,灵敏度矩阵A可由子镜位姿微小误差δx与像差变化量δL获得.

(4)

由式(4)求解Moore-Penrose广义逆可得到子镜位姿误差

ΔX=A+ΔL

(5)

值得注意的是,在一定小范围内才具备该式的线性关系,但超出小范围误差情况时,仍可使用该式进行迭代调整.数次调整后的像差将处于小范围内,重新具备线性关系,则可继续求解调整直至像差收敛满足要求.

3 分块镜调整机构设计与整星模型建立

3.1 整星动力学

分块式空间望远镜各子镜以卫星上表面的大型平整基座为底座,依次拼接安装在卫星上,且认为各子镜主动调整机构下平台与星体安装紧固无误差,各下平台与星体组成下平台系统.在星体进行小位姿稳定控制时,各子镜主动调整机构才开始进行测量和位姿调整.

图2展示了分块式空间望远镜卫星的整体结构示意,其中星体所受振动主要考虑柔性附件与角动量装置等微振动源影响.图中已详细标注出本文关注的各子镜、主动调整机构和星体等主要部件坐标系以及建模点的位置,而各扰动部件的坐标系如柔性附件坐标系fak(Oakxakyakzak)、角动量装置框架坐标系fgi(Ogixgiygizgi)、转子准几何体坐标系ffi(Ofixfiyfizfi)、转子几何体坐标系fwi(Owixwiywizwi)和转子惯量主轴坐标系fIi(OIixIiyIizIi)在本文中不再详细标注,后续将直接给出推导后的扰动方程.

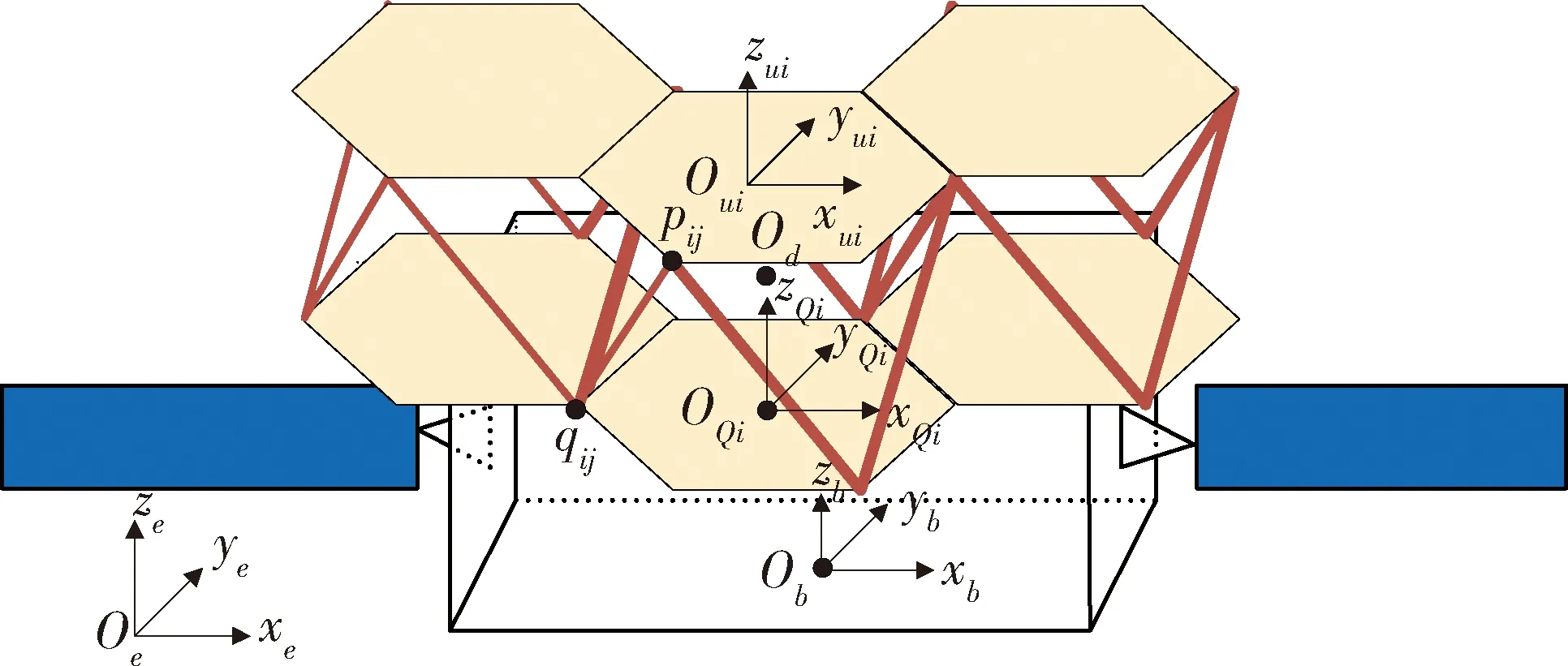
图2 分块式空间望远镜卫星示意图

定义分块式空间望远镜的主卫星质心为Ob,卫星上表面中心为Od,第i个子镜下平台质心为OQi,上平台(子镜面)质心为Oui,第j根支杆与上下平台的连接点为pij和qij.建立惯性坐标系fe(Oexeyeze)、卫星本体坐标系fb(Obxbybzb)上镜面坐标系fui(Ouixuiyuizui)和下平台坐标系fQi(OQixQiyQizQi).在fb(Obxbybzb)下,rdb为Ob到Od的位置矢量,Qi为Od到OQi的位置矢量;在fui(Ouixuiyuizui)下,pij为Oui到pij的位置矢量;在fQi(OQixQiyQizQi)下,qij为OQi到qij的位置矢量.利用Kane方法建立带有N个子镜的整星动力学方程如下:

(6)

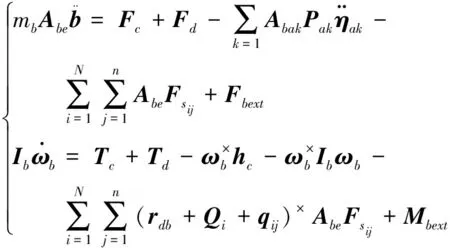
(7)

微振动源中柔性附件振动方程为

(8)

微振动源中角动量装置采用最小范数伪逆操纵律,主要考虑其静动不平衡量,其转动方程和扰动方程为

(9)

3.2 子镜主动调整机构

图3展示了子镜主动调整机构的三维模型与示意简图,标注了建模需要的坐标系.机构以Stewart六自由度并联平台为设计基础,采用CUBIC构型,支杆间两两正交.机构主要包括上平台(镜面)、下平台、音圈电机驱动单元和电涡流传感器组成.音圈电机驱动单元包含音圈电机、光栅尺和驱动控制器,电涡流传感器包括传感器主体和安装支架.

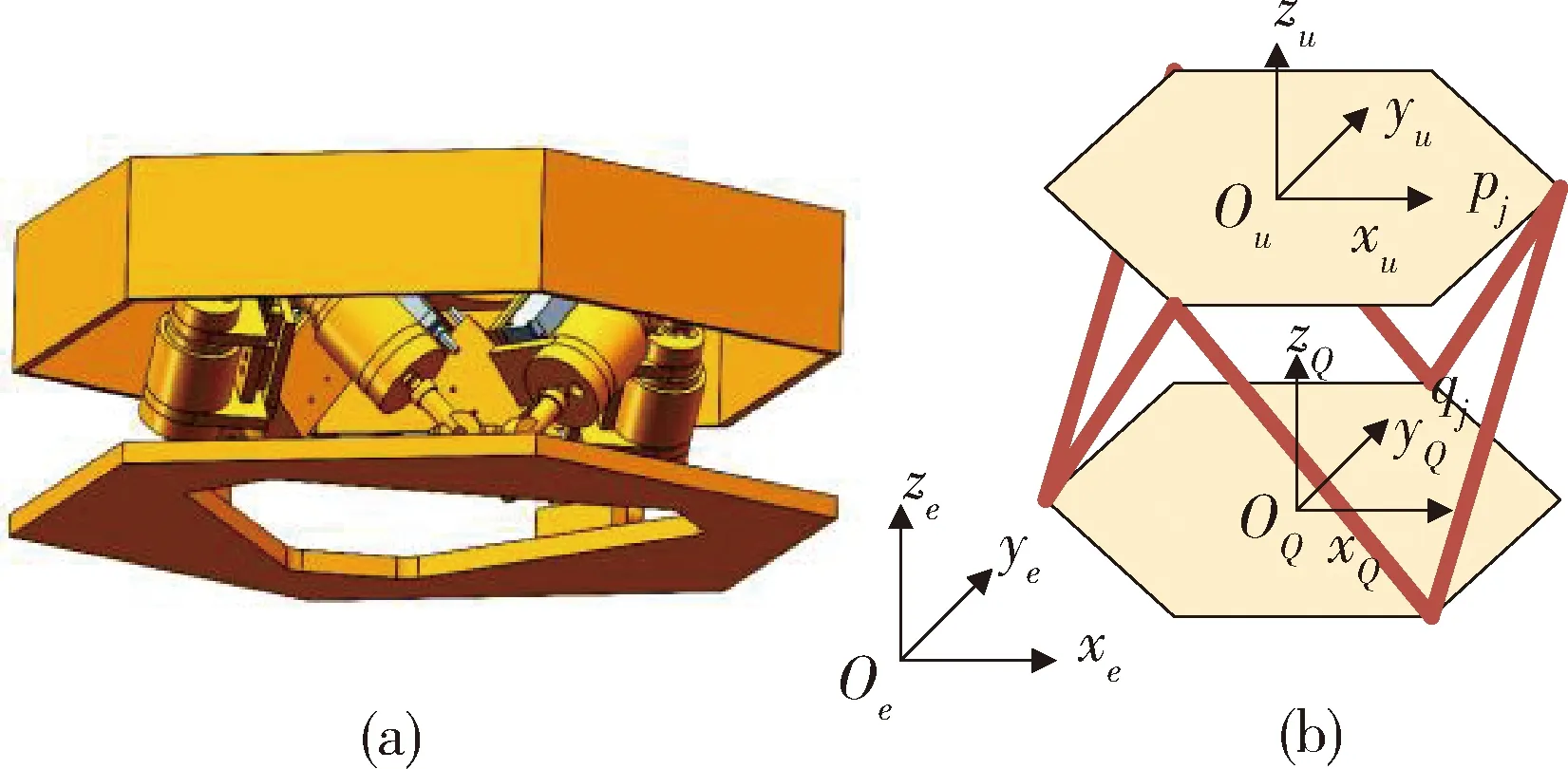
图3 子镜主动调整机构三维模型与示意简图

图4展示了主动调整机构实物,包括其内部如音圈作动器、鱼眼接头等各部件连接形式.音圈作动器使用圆柱音圈电机,为直线运动形式.其动子与定子两端安装有加工的外螺纹柱,与鱼眼接头(中心鱼眼可在一定角度内全向转动,与球铰类似)拧紧固定后,再用对应尺寸螺栓穿过鱼眼接头中心孔与镜片、下平台预留安装孔拧紧,即可完成音圈作动器与上下平台的连接.同时,与定子固定的大L型板底部安装有滑轨,与动子固定的小L型板底部安装有滑块,滑轨与滑块对接准确后定子与动子即可实现在同一圆心水平的直线顺滑移动,且定子与动子的内、外壁之间不接触.测量用的光栅尺的标尺光栅和光栅读数头分别安装于小L型板侧面和大L型板底部,标尺光栅随着动子带动小L型板运动而移动,固定的光栅读数头测量移动距离完成读数.

图4 子镜主动调整机构实物

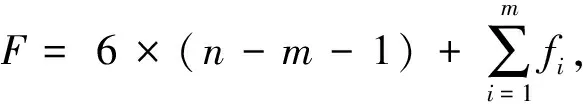
针对第i个子镜主动调整机构,分别建立惯性坐标系fe(Oexeyeze)和上、下平台坐标系.fu(Ouxuyuzu).和fQ(OQxQyQzQ),上、下平台坐标系原点位于各自质心处.音圈电机驱动单元组成的作动支杆在上、下平台的连接点分别为pj和qj.依据几何关系及矢量封闭性,进行子镜主动调整机构运动学建模.

惯性系下,连接点pj和qj的位置矢量及速度矢量为

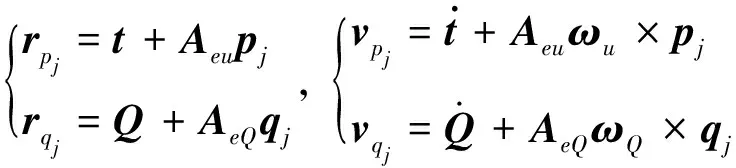
(10)

其中,t和Q分别为上下平台质心在惯性系下的位置矢量;Aeu和AeQ分别为fu和fQ到fe坐标系的转换矩阵,采用3-2-1旋转;ωu和ωQ分别为上、下平台在fe坐标系中的角速度矢量;pj和qj分别为第j根支杆与上下平台连接点在fu和fQ坐标系下的位置矢量.由此得到支杆相关量表达式

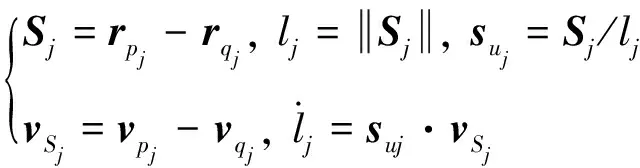
(11)

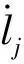
考虑下平台锁定且fQ与fe坐标系重合时,主动调整机构的运动学关系可由式(11)写为

(12)

由于子镜的共焦共相位调整一般均为微幅调整,则各物理量均为小量.对于CUBIC构型的Stewart平台,平台雅可比矩阵可认为常值[25].因此结合式(12)可得

Δl=JΔX

(13)

对于子镜调整机构的调整量TTP而言,Δl=J*[ΔzuΔφuΔθu]T,其中J*为J取第3、4、5列组成的冗余雅克比矩阵.由此便可计算调整TTP误差所需的支杆长度变化量,也可计算杆长或者位姿控制误差的对应调整量.

3.3 位姿解算方案

针对子镜在X、Y方向的倾角误差δθx、δθy即上平台相对下平台的相对倾角φ、θ,以及Z方向的高度差Δz,采用电涡流传感器阵列并设计位姿解算方案的方式获得.

图5 电涡流传感器阵列布置方案

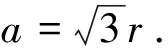
在小量调整下,分别令1)θ和Δz为0;2)φ和Δz为0;3)φ、θ为0.由几何关系获得如下方程:

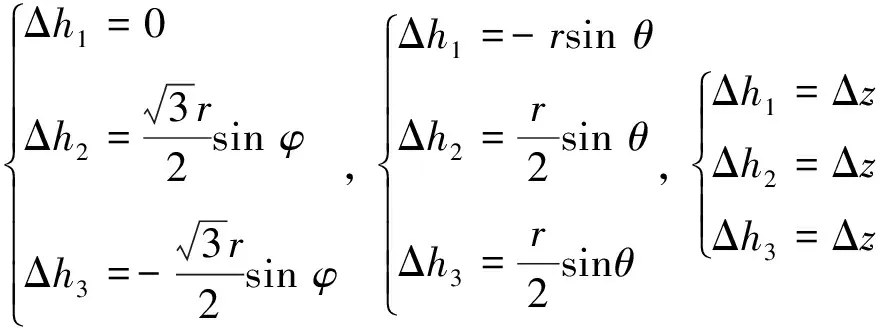
(14)

并进一步近似得到

(15)

对于N个子镜的位姿解算,第i个子镜的涡流传感器阵列测量值为Δhi,TTP误差量为ΔTTPi,则分块式空间望远镜的全部子镜位姿解算紧缩矩阵为

(16)

4 合像与振动一体化控制

4.1 整星控制方案

在单个子镜主动调整机构的控制中,在各个作动器支杆的特性相同且单支杆高性能控制的前提下,采用直接对作动器支杆的分散控制降低了控制难度,提高了控制系统稳定性.在分块式空间望远镜的整星控制中,由于各子镜的特性相同,同样考虑采用分散式控制的方法进行共焦共相调整.

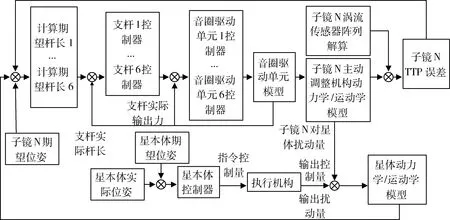
图6 分块式空间望远镜整星控制方案

4.2 子镜及音圈驱动单元控制

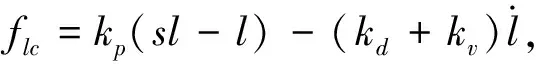
而在具体的驱动单元中,音圈电机因其高精度、高频的特点而广泛应用于各行业的精密控制领域.其电压平衡方程、动力学方程和电-力方程为[26]

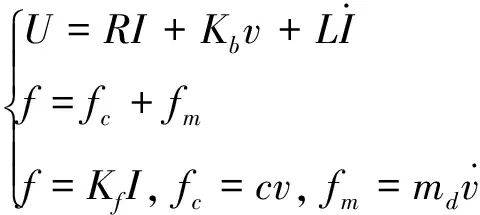
(17)

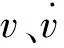
将式(17)进行拉式变换得到电机输出力fm与电压U和动子速度v的传函为

fm(s)=G1(s)U(s)-G2(s)v(s)

(18)

其中,

(19)

由式(18)与(19)可知,动子速度v将对音圈电机的输出力产生扰动作用.音圈电机高精度的输出力控制是子镜高精度位姿调整的关键,而实际使用时动子的速度可由光栅尺直线编码器准确获得,因此考虑使用前馈加反馈的控制方式消除扰动.

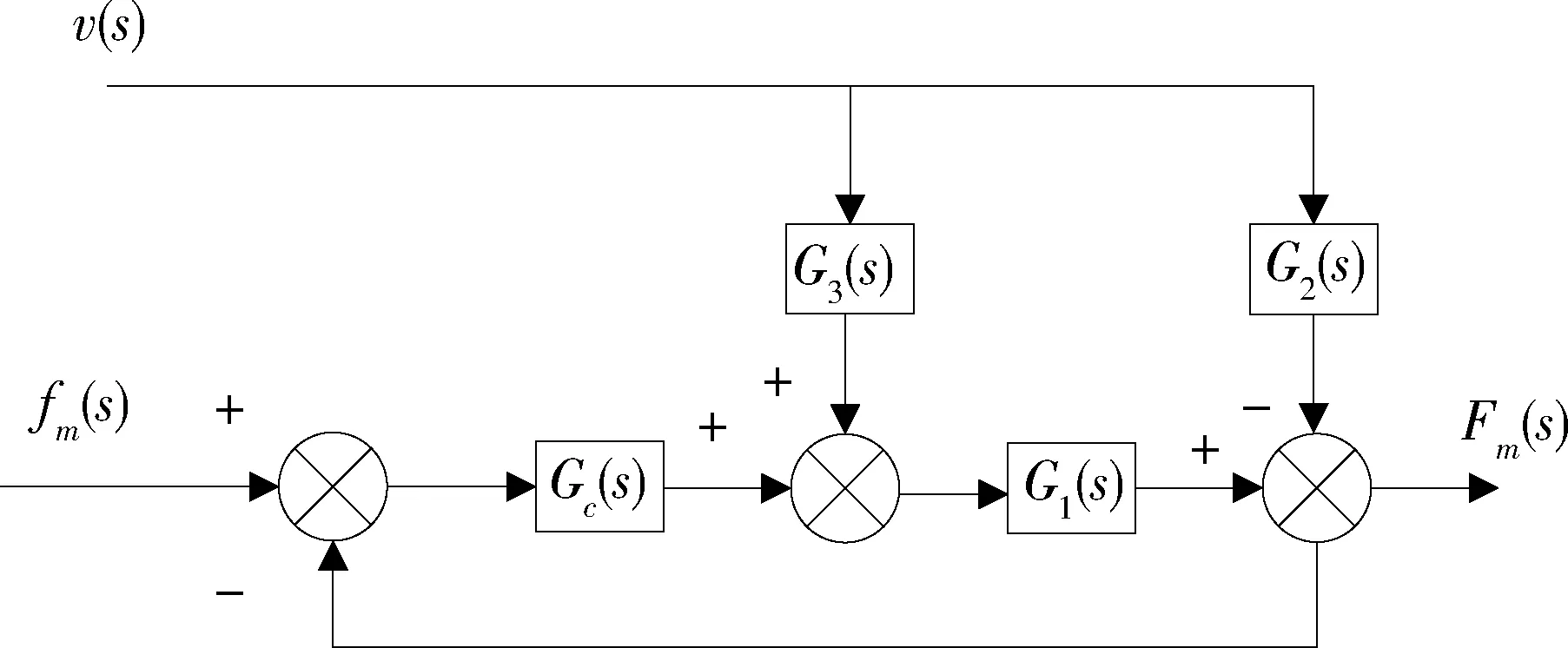
图7 音圈电机前馈-反馈控制方案

其中,Gc(s)为音圈电机反馈控制器传递函数,G3(s)为前馈补偿传函.由前馈补偿原理知

(20)

由于实际应用是无法实现此具有微分特性的前馈补偿,考虑在分母中配置一个极点的方式解决,相当于串联一个一阶RC滤波器.音圈电机动子速度v频率可以非常高,应用在该子镜主动调整机构中时,音圈电机动作变化速度不会很快,但由于同时兼顾高频隔振,因此考虑滤波器截止频率ωc需设置较高.

(21)

5 试验实例

5.1 仿真参数

以6个子镜为例进行仿真验证,星体带有一对帆板和金字塔构型陀螺群.

表2 仿真参数

5.2 仿真与试验结果

(1)音圈电机前馈PI控制仿真:分别给定稳态期望力f=10和动态期望力f=5sin(2π·50t).

从图8可以看到,该音圈电机的稳态保持和动态跟踪输出力效果都较好,在5 ms跟上期望力,跟踪速度快;输出力误差在10-3N量级,稳态精度高;高频跟踪过程中,无相位延迟和明显超调.这证明设计的前馈PI电流环控制器能保持音圈电机高频高精度的输出力控制,有效抑制扰动.

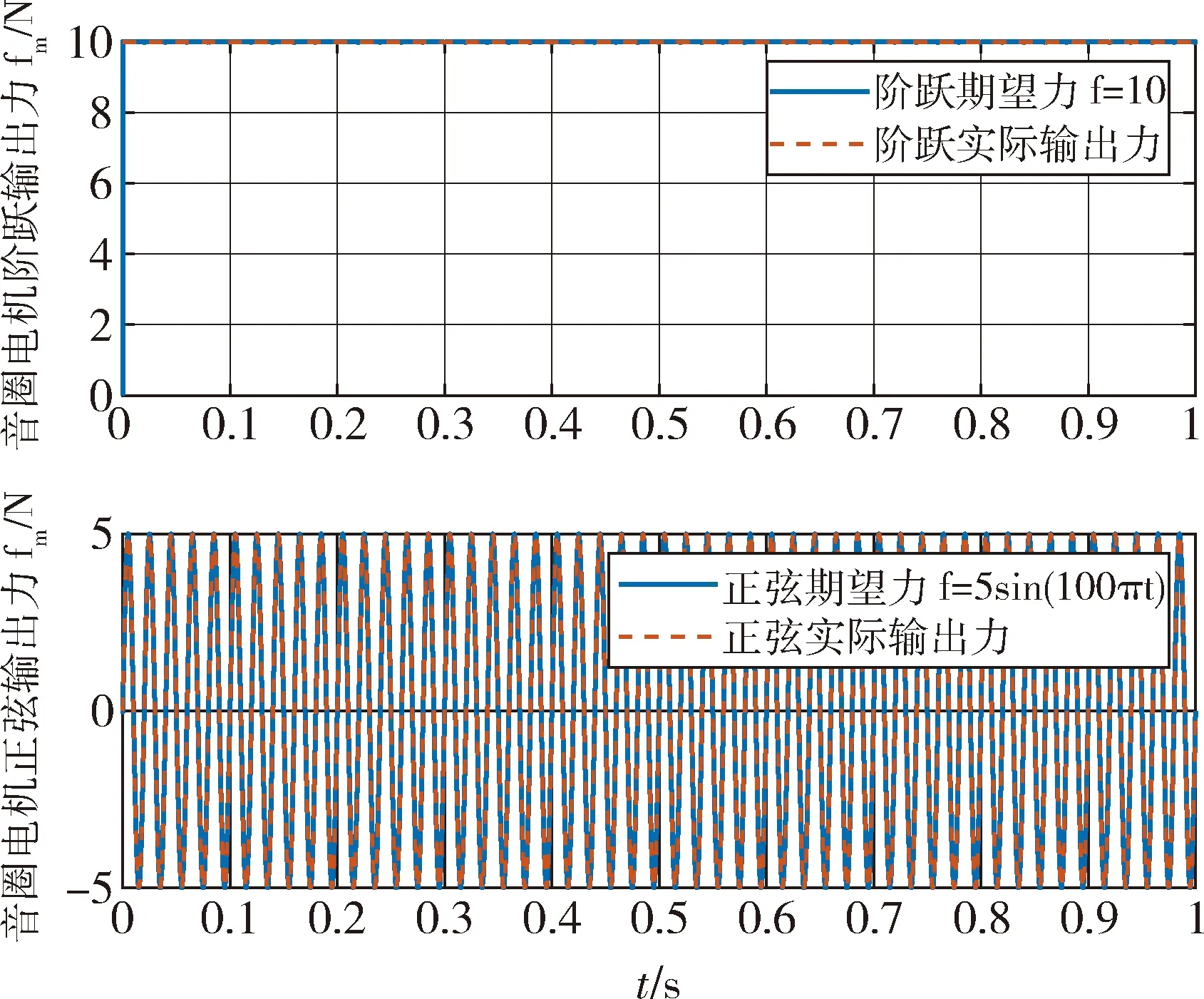
图8 音圈电机输出力控制仿真结果(f=10,f=5sin(100πt)

(2)双子镜参考调整试验:采用静平台与动平台结合的试验方案,2个平台的结构、尺寸、部件完全相同(外接圆Φ40 cm);唯一区别为静平台的作动器支杆为加工模拟件,尺寸与动平台的实际作动器支杆相同;2个平台中心都均布3个电涡流传感器,通过相应的位姿解算方案算出各自的绝对位姿,并以静平台为基准,求差得到镜片相对位姿误差.

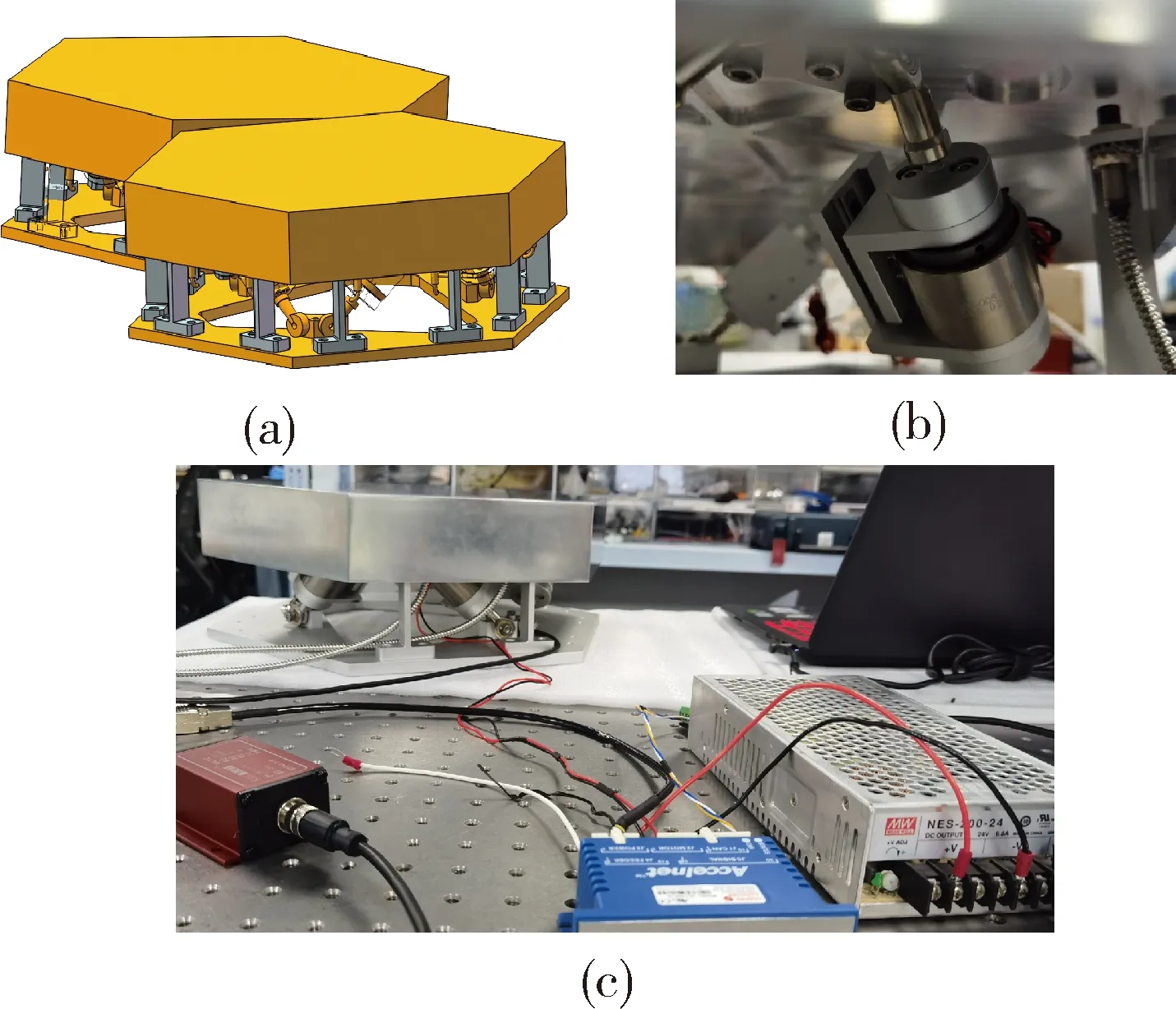
图9 双子镜调整试验原理及实物图

由于静平台不动,其位姿作为参考位姿,动平台以该参考位姿为中心绕X轴正弦微幅摆动.可以看到,与理想的蓝色正弦曲线相比,平台姿态运动始终追踪理想轨迹,红色实际姿态曲线存在一定的抖动与偏差.分析原因总结为设备装配过程存在装配误差,此为常值偏差;音圈电机驱动单元的实际工装存在间隙,导致运动时存在轻微晃动而形成镜面的轻微抖动.

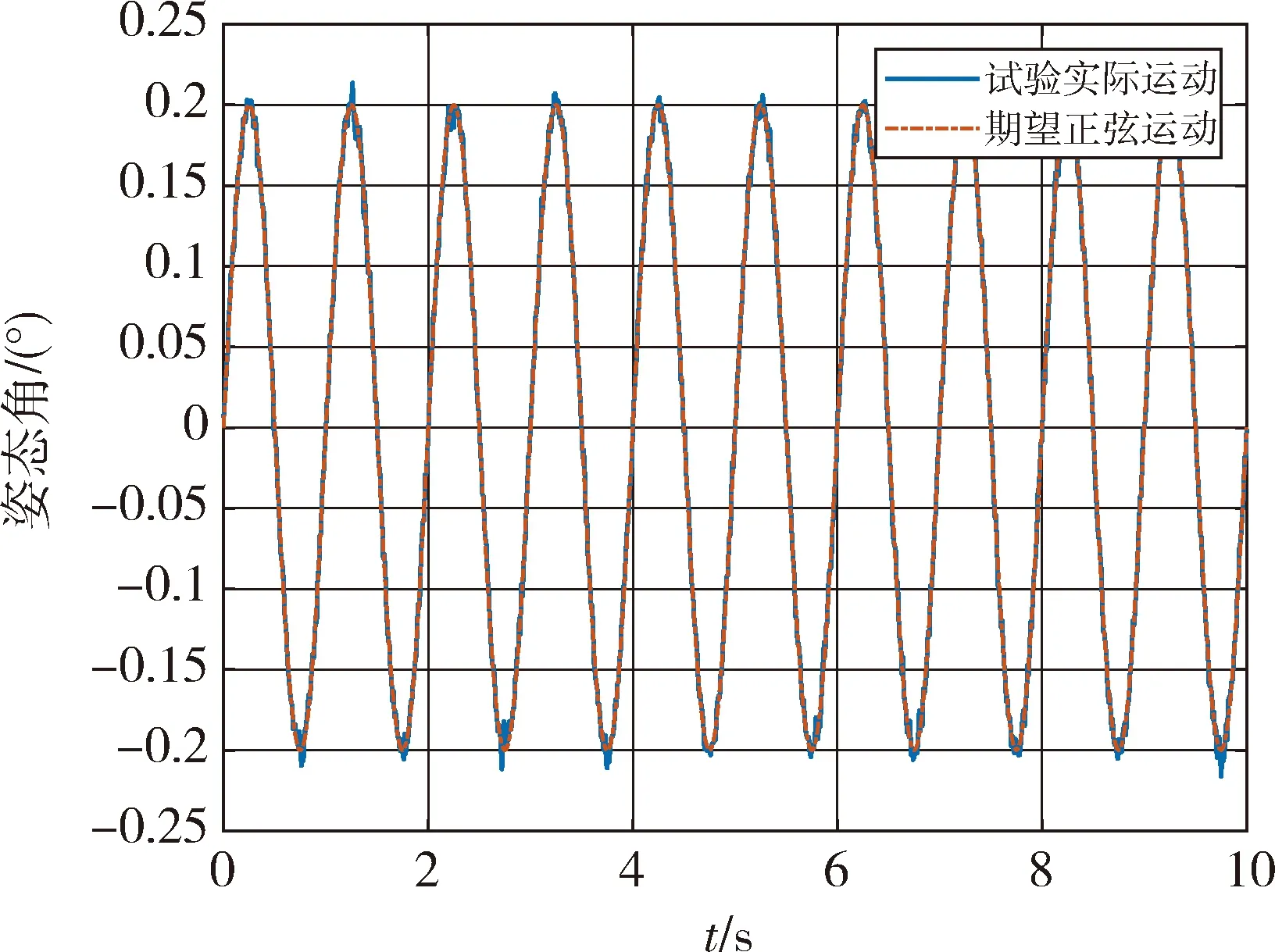
图10 双子镜调整试验结果

(3)分块式空间望远镜整星双闭环TTP控制:星体执行位姿稳定PD控制,主镜各子镜执行初始TTP误差消除控制.

从图11可以看出,星体位姿稳定控制时受到各子镜对其扰动作用而产生位姿偏差,但在后期星体与各子镜都逐步调整到位后,星体位姿也收敛稳定,位置和姿态精度在10-6m和10-3(°)量级.从图12～14各子镜的TTP误差均得到快速调整和控制,在10 s左右初步收敛,并在40 s内最终振荡收敛实现X、Y方向倾角误差在10-4(°)即1″量级,Z方向平移误差在10-8m即10 nm量级.

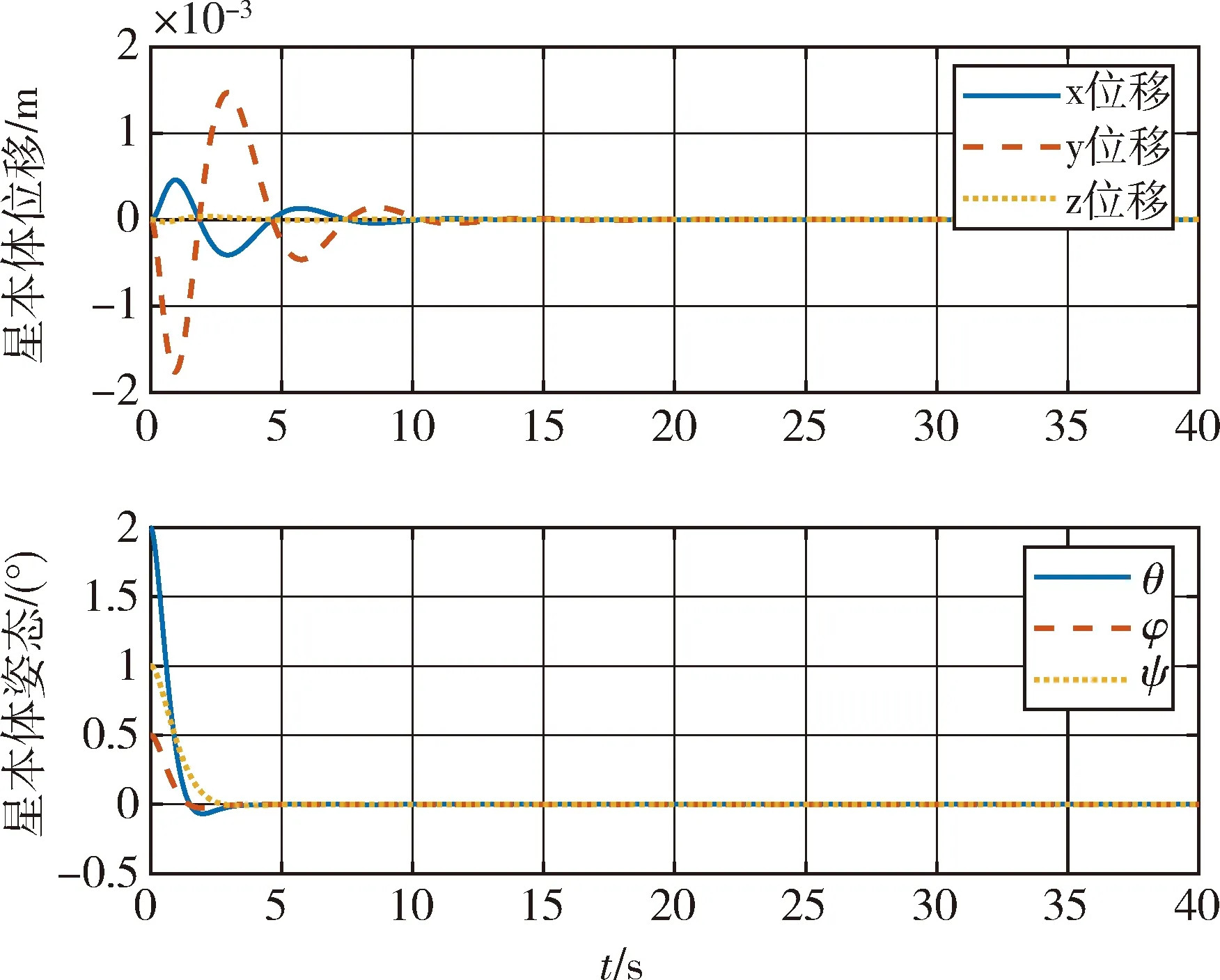
图11 星体位移和姿态

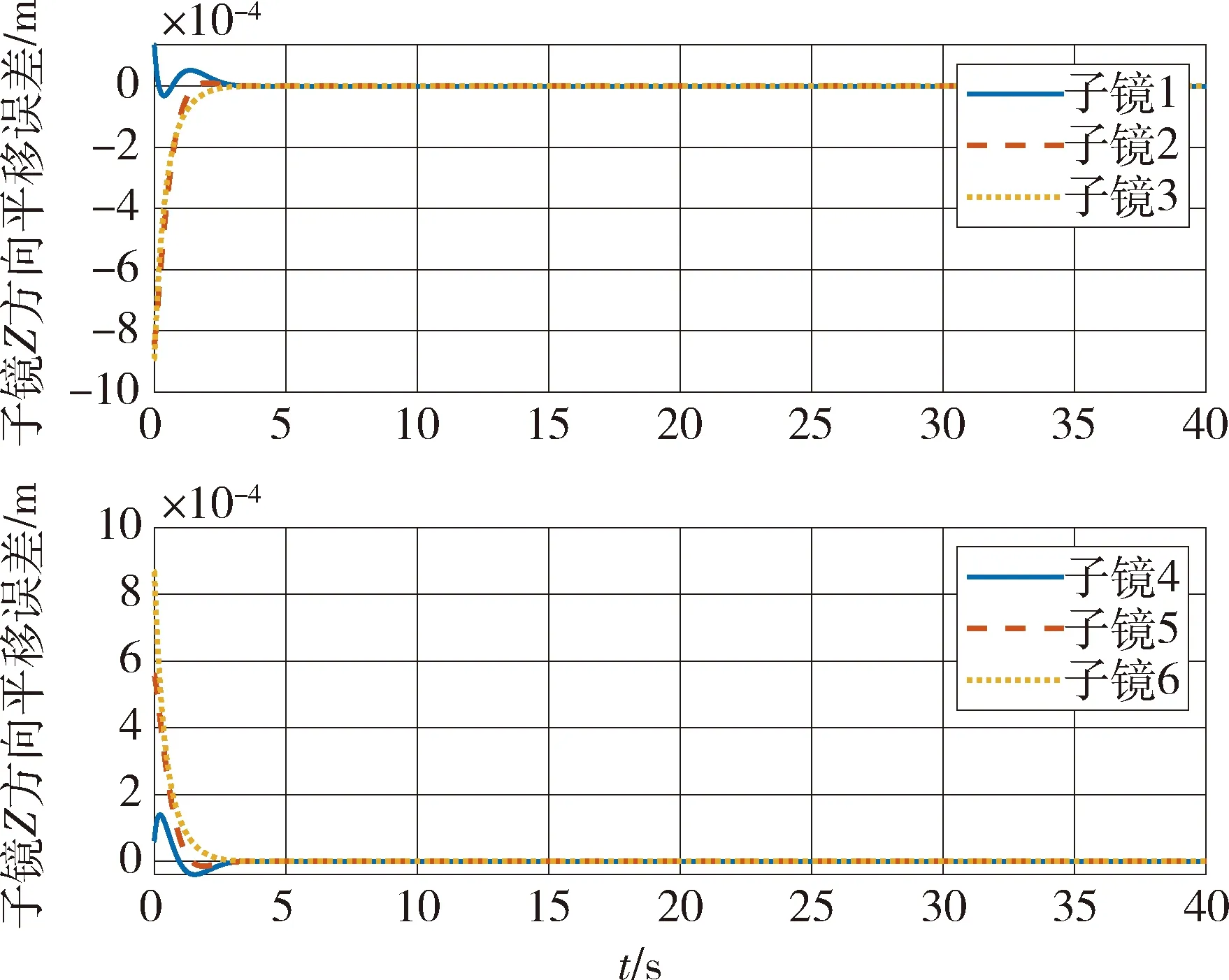
图12 子镜Z方向平移误差

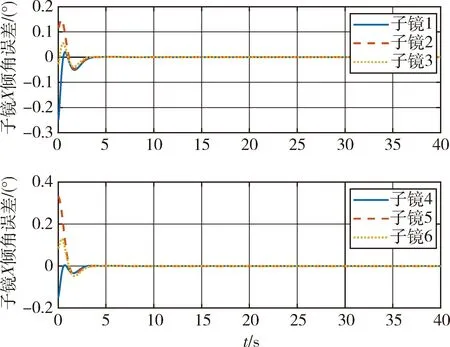
图13 子镜X方向倾角误差

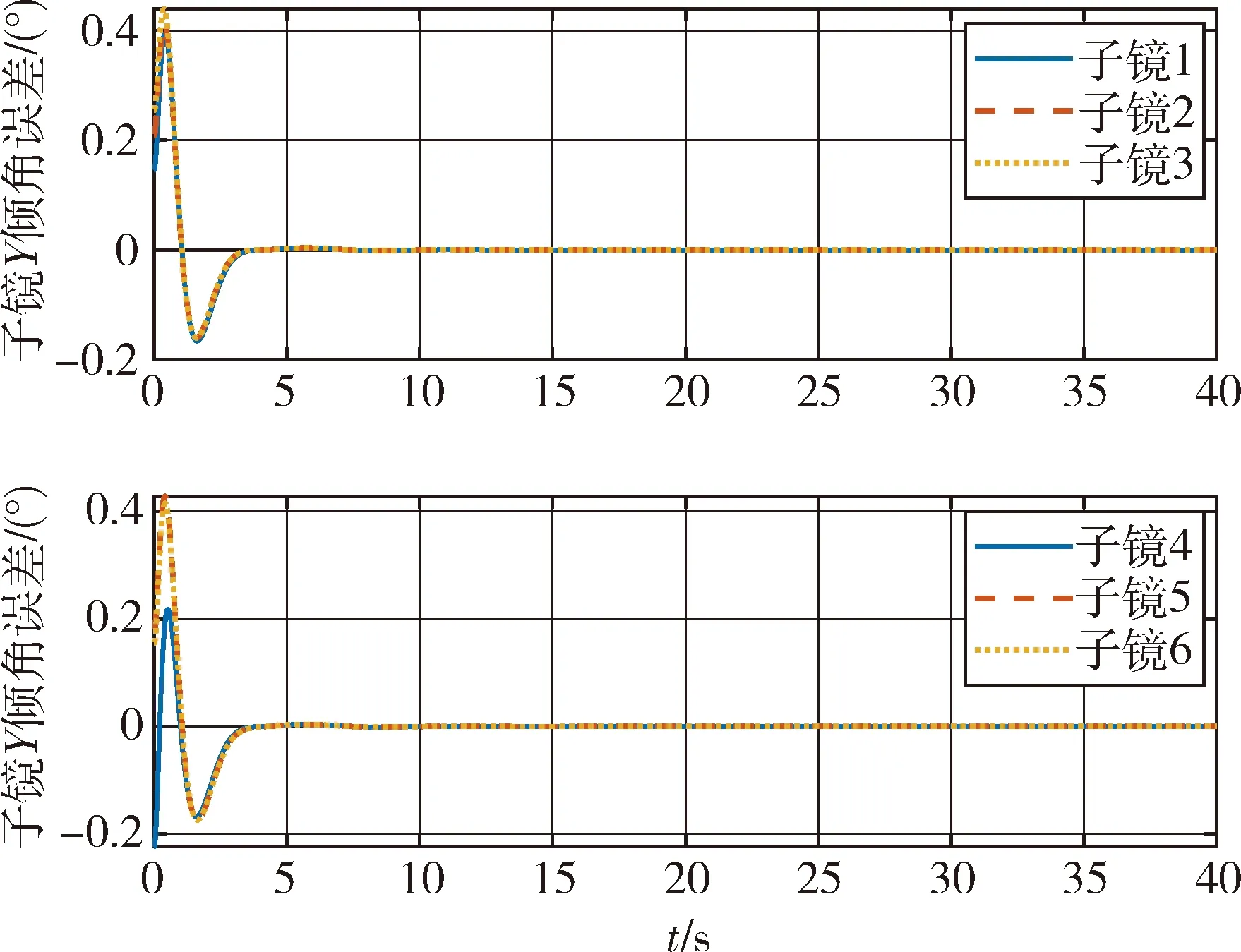
图14 子镜Y方向倾角误差

在主动调整机构的运动调整与振动控制下,各子镜的TTP误差快速同步收敛,合像速度相较于目前传统电机配合精密机械机构长达数周乃至数月的调整时间大大缩短,仿真时各子镜同步实时调整.

以上误差分析中,星体为绝对误差,子镜误差为相对误差,而分析隔振效果时需要统一表示为绝对误差才可比较.在仿真过程中,虽然给定的控制目标为子镜相对位姿,但仿真过程中实际计算的为子镜绝对位姿,再通过与星体实际位姿比较计算得到相对位姿和实际杆长等信息.因此,将仿真后期的子镜绝对位姿与星体绝对位姿比较,以子镜1的绝对位姿误差为例,可知其位置精度在10-7m接近10-8m量级,姿态精度在10-4(°)量级.与星体位姿精度相比较,子镜位姿精度提高1～2个数量级,这也表明主动调整机构的隔振效果良好,实现了合像/振动一体化控制,避免了目前空间望远镜合像与振动调整各自需要额外部件的问题.

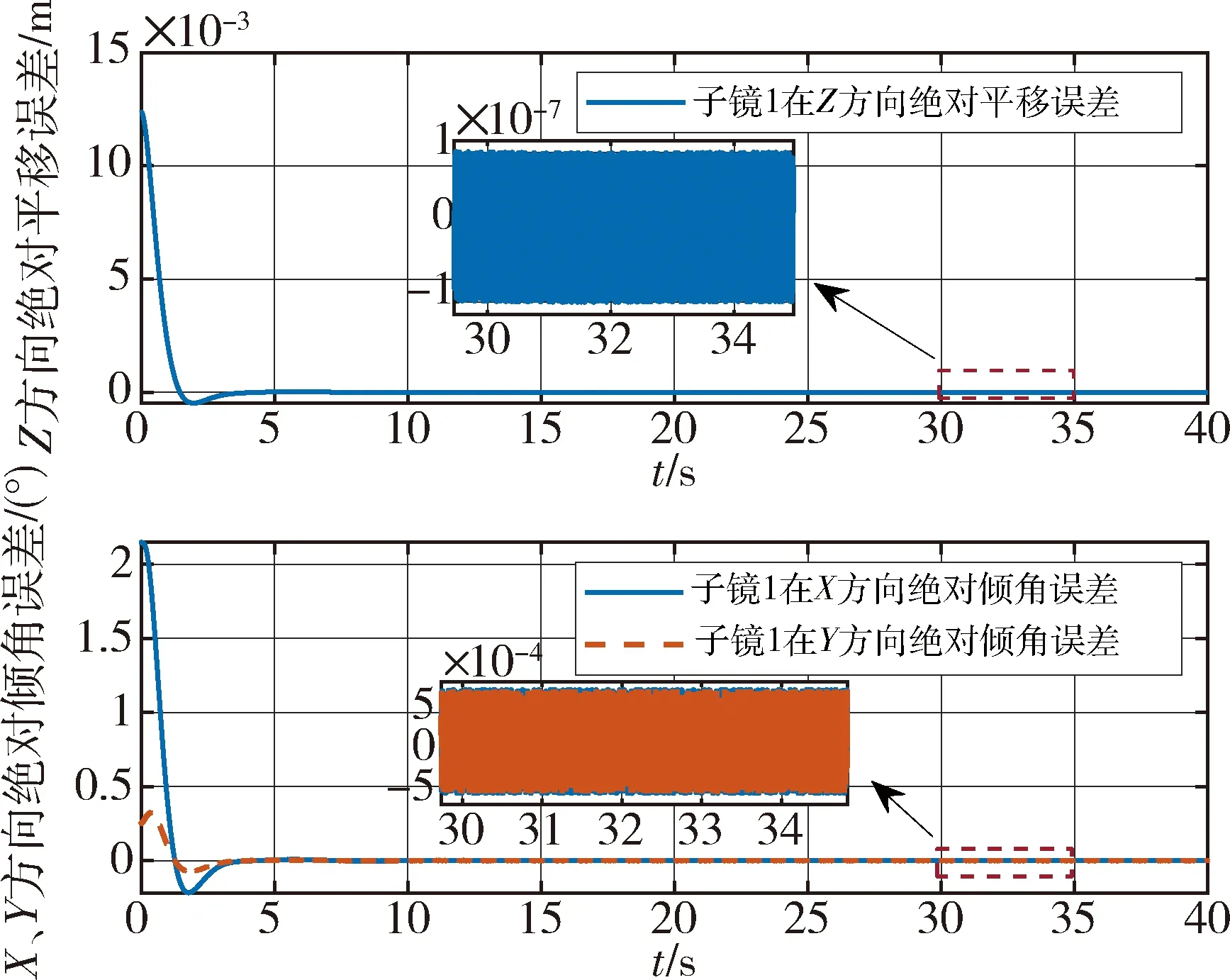
图15 子镜1绝对位姿误差

计算得到6个子镜的相位误差均方根值RMS为16.1 nm,这与詹姆斯·韦伯望远镜10 nm的相位误差均方根值相当.而分块式空间望远镜一般使用红外光波段λ=780 nm～1 mm进行成像探测,要求子镜相位误差均方根值在λ/20=39 nm以内,更高的要求在λ/40=19.5 nm.与目前的仿真结果相对比,表明本文设计的合像/振动一体化控制方案的实现指标处于国际前沿要求范围内.

计算分块式空间望远镜共相位误差与成像质量的Strehl比值S.R

(22)

式中,n是分块镜数目,σ=4πδ/λ,δ为各子镜Z向平移误差的均方根值.由此计算得到S.R值为0.99,而一般认为S.R≥0.95即表示望远镜光学系统有优良像质,对比S.R的标准可以说明本文的模型与控制方案在6个子镜的主镜系统验证中可以获得良好像质.

6 结 论

本文面向在轨组装的分块式空间望远镜主镜高精度合像与稳像调整问题,建立Zernike多项式像差与子镜位姿误差的灵敏度矩阵,揭示出子镜TTP误差的光学像差影响机理.对此建立整星动力学模型,设计子镜主动调整机构并推导涡流传感器阵列的位姿解算方案.设计整星的合像与振动控制方案,考虑音圈电机驱动单元特性设计分散式前馈补偿控制器.仿真结果表明音圈电机力跟踪速度5 ms、误差在10-3N,各子镜相位误差RMS为16.1 nm,Strehl比值为0.99.像差与子镜位姿误差的光学灵敏度反演解算方法运算量小、效率高,设计的音圈电机主动调整机构结构简单、调整速度快、精度高,能有效完成子镜位姿调整和振动控制,整个分块式空间望远镜光学系统具有良好成像效果.