小天体SPC特征导航过程中特征选取原则研究

王安然, 王 立, 张成渝, 田启航, 华宝成, 刘姝含, 李 林

北京控制工程研究所, 北京 100094

0 引 言

小天体探测已经成为近年来深空探测的热点.深入了解小天体的本质、形成与演化机理,有助于人类探索生命起源与太阳系奥秘等一系列科学问题[1].目前,小天体的探测方式主要包括交会、飞越、环绕、撞击、着陆采样等[2],其中最直接的手段就是着陆到小天体表面进行探测.随着小天体探测技术的发展,各国也依次开展了小天体着陆探测任务.1996年2月17日,美国宇航局(NASA)发射了世界上首个小天体着陆探测器“NEAR Shoemaker”,并成功着陆小天体433Eros[3].2004年8月,欧洲航天局(ESA)发射Rosetta探测器着陆彗星67P进行探测[4].2007年9月27日美国发射拂晓号(Dawn)探测器探测谷神星(Ceres)、灶神星(Vesta)[5].2003年9月,日本发射了“隼鸟”1号(Hayabusa 1)探测器用于探测25143号小天体 Itokawa,该探测器成功实现了小天体的着陆与采样返回任务[6];之后日本于2014年12月又发射了“隼鸟”2号(Hayabusa 2)探测器对Ryugu小天体进行着陆探测及样本采样返回任务[7];2016年8月NASA发射了OSIRIS-Rex探测器对贝努(Bennu)小行星进行样本采样返回任务,目前该任务已完成采样阶段,并于2021年5月与小天体分离开始返回地球[8-11].小天体探测任务已经被列为我国深空探测四项重大任务之一[12].我国计划通过一次发射先后探测两个目标,同时实现小天体的附着、采样返回等任务[13-14].

在小天体探测过程中,由于小天体体积较小,先验信息较少,如何实现小天体精确导航和安全着陆是小天体着陆探测过程中的关键问题.光学导航方法由于其高导航精度被越来越多的应用到小天体的着陆导航过程中.着陆段的光学导航方法通过在目标天体上提前提取特征,将其与飞行器着陆过程中的拍摄图像进行匹配,从而确定飞行器在小天体坐标系下的三维位置.此过程的关键在于特征的选取,通常使用的特征包括人为制定的特征描述符(如Harris、SIFT等)以及岩石、陨坑等自然特征[15].人为制定的特征描述符容易受到光照、尺度变化等因素的影响,同时小天体表面或着陆点周围可能存在没有明显的岩石或陨坑的情况.Gaskell等[16-18]提出了一种基于SPC(Stereophotoclinometry)特征的导航方法.SPC 特征是利用SPC方法对小天体表面的某些局部区域进行三维重建,将得到的局部区域的高程值和反射率值等数据作为特征信息.相对于SFS(shape from shading)、SFM(structure from motion)等三维重建方法,SPC所需图像数量相对较少,且能通过迭代过程求解坡度、反照率、相机位姿等精确信息,且该方法能得到与图像分辨率相当的三维重建结果.SPC方法已成为小天体着陆导航过程中的主要方法,并在多个小天体着陆探测任务中进行应用,包括Rosetta、Dawn以及OSIRIS-Rex等.

但目前对SPC 特征的选取仍然缺乏依据,主要凭借经验采用手动选取特征的方式,使得特征选取的过程工作量大、效率低且主观性较强.本文对小天体着陆过程中的SPC特征的制备、渲染匹配以及位姿解算等过程进行研究,并总结出此过程中存在的问题.针对上述问题,本文提出特征选取的四项基本原则:可制备性、特异性、光照适应性以及分布均匀性等,并设置特征选取的阈值条件,使得特征选取过程有据可依,从而简化特征筛选过程,提高特征选取效率.并引入PDOP(position dilution of precision)值对特征的分布结构进行评价.

1 特征定义

在使用SPC特征进行小天体着陆导航的过程中,需要用到的坐标系有小天体坐标系、特征局部坐标系以及相机坐标系等.其中小天体坐标系为以小天体质心为原点,自转轴方向为Z轴(图1中的Bz),XOY面为小天体赤道面的右手坐标系;特征局部坐标系以选定特征位置的中心点为原点,其Z轴沿小天体质心与特征中心点连线方向向上(图1中的Uz),过特征中心点且垂直于Z轴的平面为XOY面;相机坐标系以相机光心为原点,主光轴方向为Z轴指向(图1中的Cz),平行于成像平面的列、行方向为X轴和Y轴指向,相关坐标系的示意图如图1所示.图中特征中心点在小天体坐标系下的位置向量为V;W是相机坐标系原点在小天体坐标系下的位置;i和e分别为太阳方向向量和相机方向向量与特征中心点处的表面法向量的夹角;α为相位角.

SPC特征是指使用SPC三维重建方法得到的小天体某些局部区域的地形数据块,主要由以下几部分构成:1)特征中心点在小天体坐标系下的位置;2)在特征局部坐标系下特征块的高程数据和反照率信息;3)特征局部坐标系与小天体坐标系之间的转换关系等,特征如图1中的白色部分所示.在进行SPC导航过程中,特征位置的选取十分重要,不同的特征会对后续陆标制备及匹配导航过程的可靠性和精度产生影响.

2 特征选取原则

在小天体着陆过程中使用基于SPC特征导航方法的一般流程如图2所示.

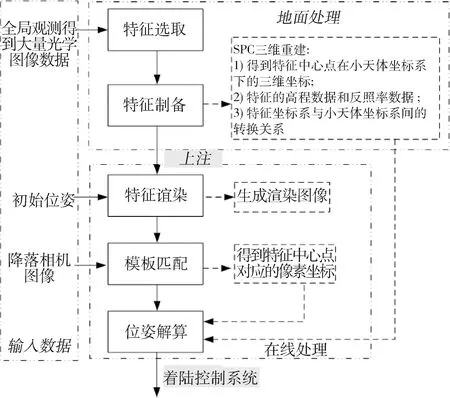
图2 利用SPC特征的小天体着陆导航流程

在地面上,首先利用小天体全局观测过程中相机拍摄的大量小天体不同光照条件和不同位置的光学图像,进行特征区域选取;然后利用SPC三维重建方法对选取的特征进行制备,并将制备得到的特征信息上注到机上.

在飞行器着陆下降过程中,首先根据飞行器的初始位姿对上注的特征进行渲染,生成与飞行器飞行时刻对应的二维渲染图像;然后利用模板匹配的方法将生成的渲染图像与飞行器实时拍摄的降落图像进行匹配,从而得到拍摄图像上对应的特征中心点的二维像素坐标位置;最后根据多个特征中心点在小天体坐标系下的三维位置及其对应的图像像素坐标,即可解算出飞行器在小天体坐标系下的实时位置,并将此结果输出给着陆控制系统.下面通过对上述SPC特征导航过程进行分析,对特征选取的区域进行反约束,从而确定适用于小天体着陆导航过程的特征选取原则.

2.1 特征可制备性

SPC技术需要根据多张不同位置和光照条件下拍摄的图像计算地形高度和表面反照率[19].SPC进行三维重建的主要过程为:

1)根据式(1)的相机成像模型得到小天体局部坐标系中的某点x=(x1,x2,h)对应的在第k张图像上的灰度值Ek(x).其中X=(X1,X2)是x点对应的图像像素坐标,f为相机焦距,V和W为小天体坐标系下的特征中心点和相机中心点的位置,c为相机坐标系与小天体坐标之间旋转矩阵,u是特征局部坐标系与小天体坐标系之间的转换矩阵.Mij=ci·uj为将特征局部坐标系转换到相机坐标系的转换矩阵.

(1)

2)第k张图像上的灰度值也可由式(2)得到,其中Ik(x)为第k张图像的灰度值;Lk为乘常数;a(x)为相对反照率(归一化后的);Φk为背景常量;i和e分别为太阳方向向量和相机方向向量与x点处的表面法向量的夹角,α为相位角;R为反照率方程[20],如式(3)所示,其中L(α)=e-α/60.

Ik(x)=Lka(x)R(cosi,cose,α)+Φk

(2)

(3)

3)式(3)中的cosi和cose可以由地形梯度得到.设x处的梯度为g=(g1,g2),则有式(4),其中s=[s1s2s3]和e=[e1e2e3]是特征局部坐标系下的太阳方向向量和飞行器方向向量.

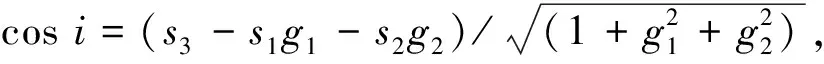
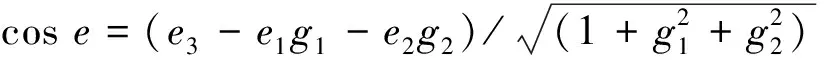
(4)

4)对于特征上每个点x,将式(3)、(4)代入式(2),可以得到Ik(x)关于梯度g1,g2和反照率a(x)的函数,通过最小化式(5)可以对梯度和反照率进行优化.其中σ由原图像亮度决定.g1,g2由高程求解过程迭代更新.通过以上过程,可以得到特征局部坐标系下的特征高程及反照率数据,这些数据构成导航过程中上注的特征信息.

Σ(Ek(x)-Ik(x))2/σ2

(5)

选取的特征需要能利用上述过程进行重建.由以上SPC的重建过程可以发现,使用SPC进行特征重建需要尽可能多的覆盖特征区域的图像,且当用于重建的图像之间拍摄角度及光照条件区别较大时有利于高程数据和反照率数据的求解.因此在选取特征时应先对全局观测过程中拍摄的图像进行相互配准,并在共视区域范围内进行特征选取.且在特征重建过程中应选取拍摄视角和光照条件差别较大的图像.

除此之外,SPC在地形高度计算过程中的约束和迭代过程会平滑掉锋利的特征边缘,如具有陡坡和大垂直起伏的区域等;且对于图像中的阴影区域,重建效果会比较差.图3(a)为特征对应的激光数据,图3(b)为利用SPC方法重建的特征地形与激光数据之间的误差,从图中可以看出,在较为陡峭的地方,SPC重建的高程误差较大,为激光获得的真实值的1/2～2/3.

图3 SPC三维重建结果与激光数据的比较

因此特征应选在非阴影区,且相对高差较小的区域,避免重建特征高程误差过大的情况.同时较小的相对高差,也可以有效避免在特征渲染过程中的自遮挡问题,使生成的渲染图像与拍摄图像相似度更高,实验表明选取特征的相对高差控制在2 m范围内较为适宜.图4(a)为全局观测过程中拍摄图像上的两个特征;图4(b)为利用SPC方法重建得到的两块特征区域对应的高程数据,其中左图相对高差在10 m左右,右图的相对高差为1.5 m;图4(c)为利用特征数据渲染得到的渲染图像,从图中可以看出,当选取的特征高程差较大时,生成的渲染图上有明显的空洞,不适合作为导航特征.

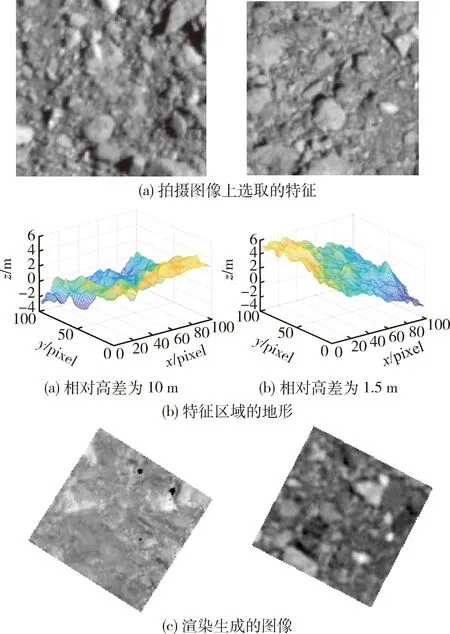
图4 不同相对高差处选取的特征对比

2.2 特征的光照适应性

在选取特征的时候,必须考虑导航使用过程中特征的光照条件,此特性可以用太阳高度角(太阳向量与小天体表面法线的夹角)来描述.当特征所处位置的太阳高度角过大时,图像较暗,容易产生大量的阴影区域,从而影响图像匹配的正确性;当太阳高度角过小时,会导致图像过亮,对比度降低,生成图像时过分依赖相对反照率的值,导致渲染图像与真实图像存在较大差异.实际着陆过程中,需要保证特征在着陆时间段内能够清晰成像,不会出现过暗或过亮的情况.如图5所示,在相同的着陆时刻,(a)特征的太阳高度角为80°,此时生成的图像过暗,利用NCC相关匹配方法式(6)将其与降落图像进行匹配,得到的匹配峰值为0.27;(c)特征对应的太阳高度角为10°,此时生成的渲染图像过亮,导致特征的模糊,匹配峰值为0.34;特征(b)在此拍摄条件下的太阳高度角为50°,可以形成较亮暗适中、特征清晰的较稳定图像,匹配峰值为0.78.实验表明,当特征对应的太阳高度角处于30°～60°的范围时,能得到成像质量较好的渲染图像,从而得到正确的图像匹配结果.

图5 不同太阳高度角下特征的渲染图像对比

2.3 特征的特异性

在得到渲染图像后,需要在特征的渲染图像和飞行器降落过程中拍摄的图像之间进行图像匹配,以确定特征对应的降落图像上的像素位置.此过程中通常使用基于灰度的模板匹配算法,用互相关系数对两张图像间的相似性进行评价.设S(x,y)是大小为m×n的降落图像,T(x,y)是M×N的渲染图像.在降落图像S中,以(i,j)为左上角点,取M×N大小的子图,计算其与渲染图像的互相关系数;遍历整个降落图像,在所有能够取到的子图中,找到与渲染图像最相似的子图作为最终匹配结果.常用的互相关系数为归一化积相关系数(NCC),如式(6)所示.

(6)

其中,E(Si,j)、E(T)分别表示i,j处子图和渲染图像的平均灰度值.大量实验表明,在小天体着陆导航过程中,当渲染图像与拍摄图像的匹配峰值(即互相关系数的最大值)大于0.6时,认为得到了正确的匹配结果,反之则认为匹配错误.

文献[21]通过对模板匹配过程的分析得到图像上梯度大的区域匹配精度较高的结论.因此为了能够得到更准确的匹配结果,需要选取的特征区域具有较高的梯度值.图6(a)为全局观测阶段拍摄的小天体表面的图像,(b)为(a)图对应的灰度梯度图.从图中可以看出图像中梯度较大的区域一般位于陨坑或岩石等具有特异性、易于识别且较周围环境更加明显的边缘区域.

图6 小天体表面拍摄图像的梯度图

由于小天体表面环境复杂,单独的陨坑、岩石等特征很容易与其他相似特征发生混淆.因此,为提高匹配的鲁棒性,选择的特征上应具有两个及两个以上的岩石或陨坑(陨坑及岩石的提取方法可参考文献[23]和[24]),如图7所示.

图7 特征特异性选取的对比

2.4 特征的分布均匀性

在特征制备过程中,可以得到特征中心点在小天体坐标系下的三维位置;经过特征渲染和匹配,可以得到特征中心点对应的在降落图像上的像素坐标.当飞行器降落过程中相机视场范围内存在多个特征时,即可得到多组特征中心点在小天体坐标系下的三维位置及其对应的降落图像上的二维位置,由此可将飞行器定位的问题转化为PnP问题[25]求解.

在得到三维点和二维点对应的匹配点对后,PnP的解算精度会受到特征点对的数目和分布的影响,此过程要求相机视场内至少有4个可观测的特征,且特征应该在视场内分布均匀.此处引入三维位置精度因子PDOP[26]来描述特征的分布特性.

假设视场内有n个特征,每个特征在小天体坐标系下的位置为(xi,yi,zi),其中i=1,2,…,n,飞行器的真实位置为(X,Y,Z),则可得飞行器到每个特征的距离Di如式(7)所示

(7)

由于特征位置存在误差,会导致飞行器的定位结果不准确,实际得到的定位结果为(X′,Y′,Z′),则

(8)

将式(8)在(X′,Y′,Z′)处进行泰勒级数展开,由于定位结果的误差相对于飞行器到各个特征的距离来说较小,所以可以省略二次项,得到

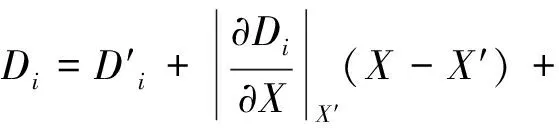
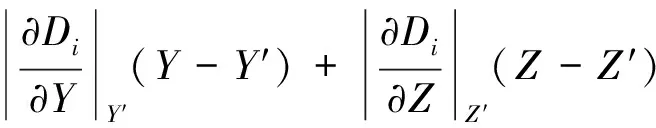
(9)

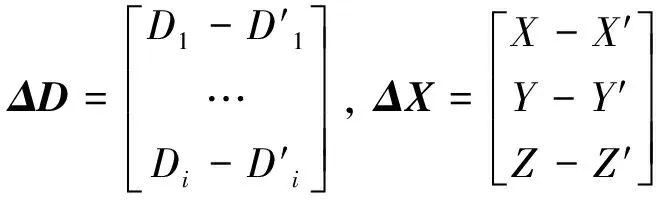
AΔX=ΔD

(10)

由最小二乘可得

ΔD=(ATA)-1ATΔX

(11)

假设ΔD同分布,且cov(ΔD)=In×nσ2.则由协方差的定义可得

cov(ΔX)=σ2(ATA)-1

(12)

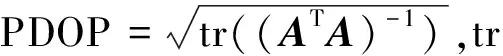
PDOP可以表征从特征到飞行器单位矢量所构成的空间形体体积.PDOP的数值越大,所代表的单位矢量形体体积越小,即特征的分布越集中,此时定位精度变差.PDOP数值较小时,代表大的单位矢量形体体积,则证明特征具有较均匀的空间分布及较高的定位精度.在特征选取过程中,可以根据飞行器的预设轨迹与特征的位置计算出不同特征组对应的PDOP值,选取其中PDOP值小的一组作为最终选取的特征.

3 实验验证

本文利用OSIRIS-Rex全局观测过程中的图像数据按照上文提到的特征选取原则进行特征筛选,得到36个大小为99×99的特征,所有特征的太阳

高度角均在30°～60°之间,均值为51.3°;所有特征区域的最大相对高差都在2 m范围内,均值为1.52 m.部分特征如图8所示,对于每个特征,左图为观测图像上选取的特征区域,右图为渲染特征后得到的渲染图像.

图8 选取的特征及其渲染图像

实验选取下降过程中距离小天体表面100 m左右是降落相机在不同位置和姿态下拍摄的11张大小为2 592×1 944的图像作为降落影像.通过图像的SPICE信息,可以计算得到该降落图像上所包含的特征情况.将选取的特征进行渲染,利用2.3节中的匹配方法与降落图像进行匹配,对匹配到的特征结果进行统计,分析得到特征的匹配率(降落图像上应匹配到的特征数与实际匹配的特征数的比值)如图9所示,其中绿色星号线为匹配率,红色直线为匹配率的平均值.

图9 特征匹配率

由图9可知,采用文中的特征选取原则选取的特征的平均匹配率达到96.85%,其中第7张降落图像中特征的匹配率较低,主要是因为部分特征在此张图像中的位置接近图像边缘,相机畸变等原因造成图像在边缘区域误差较大.在实际导航过程中,可以剔除视场边缘的特征.

对成功匹配的特征的匹配峰值进行统计,验证特征的匹配正确性,如图10所示,其横坐标为特征名称,纵坐标为该特征在多张降落图像上匹配峰值的平均值,红色直线为所有匹配峰值的平均值.从图中可以看出,特征匹配峰值均在0.6以上,且均值为0.721 5,匹配结果具有较高的鲁棒性.

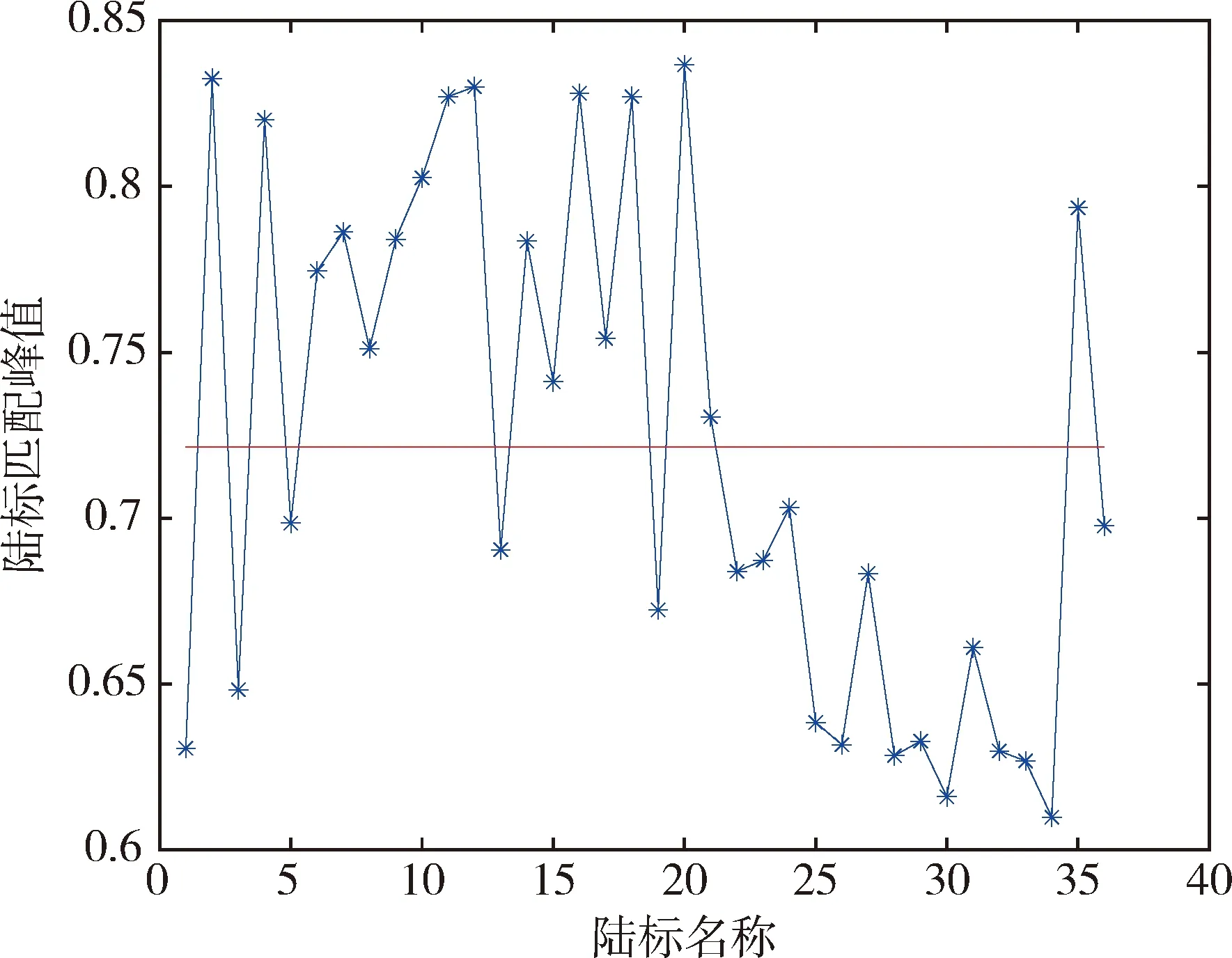
图10 特征匹配峰值

最后本文利用11张降落影像上匹配的特征进行飞行器位姿的解算,得到飞行器的位姿解算误差如图11和图12所示,纵坐标为拍摄图像时的真实位姿与解算位姿的差值.该结果表明,依照本文原则选取的特征的位置的解算精度(三维位置误差的均方根值)为0.81m,姿态精度(三轴姿态误差的均方根值)为0.22°.在小天体着陆过程中,要求飞行器的定位误差在1%以内,对应本文实验条件即要求定位误差在1m以内.实验结果表明,利用本文选取的陆标可以满足小天体着陆过程中的导航定位需求.

图11 飞行器位置解算误差

4 结 论

本文对小天体着陆导航过程中的特征选取原则进行研究,对特征的制备和使用过程进行分析,提出了特征选取的4个原则:1)可制备性,特征应选取在多张不同位置和不同太阳光照条件下拍摄的图像的共视区域,且特征区域的相对高差应控制在2 m范围内;2)光照适应性,对应着陆时刻,选取的特征的太阳高度角在30°～60°的范围内较为适宜;3)特异性,特征应选取图像梯度较大的区域,且区域内包含两个及两个以上的明显地物如坑、石等;4)均匀分布性,降落过程中相机视场范围内的特征数目应不少于4个,且选取特征组合中PDOP值大的一组作为最终的特征.实验结果表明利用上述特征选取原则选取的特征的匹配率可以达到96.85%,匹配峰值均在0.6以上,且使用选取的特征得到的导航定位精度可以满足小天体着陆导航的需求.