“一图一课”开放留白,学程导进“快慢平衡”
万周华

摘 要:“一图一课”作为微专题教学的一类课型,近来得到不少教师的关注.研发这类课型的关键在于从一个基本图形出发,开放留白,并渐次变式、拓展提升,需要教师具有一定的命题改编能力,同时又需要较强的课堂驾驭能力,包括对各个教学环节学程导进过程中的“快与慢”的平衡,还需要在小结阶段组织学生对全课所学内容进行回顾、反思与提炼.
关键词:“一图一课”;正方形;微专题
中考微专题教学越来越得到各地教研活动的关注,近期笔者所在地区在中考复习研讨会的教研活动上安排了微专题教学研究课,并有机会执教一节正方形“一图一课”的专题课,取得较好的教学效果,本文整理该课教学设计,并跟进教学立意的阐释,提供研讨.
1 正方形“一图一课”专题课教学设计
教学环节(一) 基础热身 开放探究
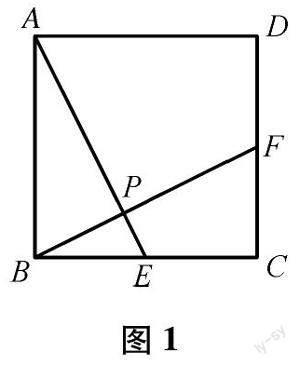
问题1:如图1,正方形ABCD中,E,F分别是边BC,CD的中点,AE,BF相交于点P.请提出一个问题(不添加条件),先在小组内交流,再全班汇报展示.
教学预设:学生经过初步思考,会提出如△ABE≌△BCF,相应得出AE=BF,AE⊥BF这类结论;如果从四点共圆的视角,还可以发现图1中除了正方形ABCD四个顶点共圆之外,还有两组四点共圆,分别是四边形ADFP,四边形CEPF的四个顶点;再从相似的视角出发,可以发现图形中直角三角形都是相似的,它们的直角边之比都是1∶2,进一步可以得出图1中EP∶BP∶FP∶AP∶AE=1∶2∶3∶4∶5.
教学环节(二) 拾级而上 一题多解
问题2:正方形ABCD中,E,F分别是边BC,CD的中点,AE,BF相交于点P.
(1) 如图2,连接PD,求证:PD=AB;
(2) 如图3,连接CP,求证:PC平分∠EPF.
教学预设:第(1)问证法较多,预设以下两种典型证明思路.
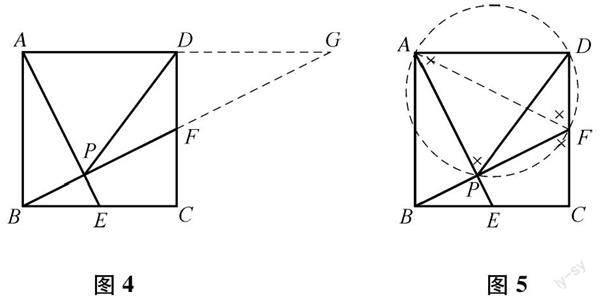
思路1:如图4,延长AD,PF交于点G,可证明△BCF≌△GDF,得到DG=BC,结合正方形的边长相等可代换得DG=AD,由“问题1”中的分析与进展可知,∠APF=90°,于是在Rt△APG中,PD是斜边AG上的中线,所以PD=AD,进而等量代换得到PD=AB.
思路2:如图5,由四边形ADFP的四个顶点在同一圆上,可连接AF,证出图5标注“×”的4个角都是相等的,即可得PD=AB.
第(2)问证法也较多,预设以下两种典型证明思路.
思路1:如图6,四边形CEPF的四个点在一个圆上,连接EF,证出图6标注“×”的4个角都是相等的,所以PC平分∠EPF.
思路2:如图7,过点C作CH⊥BF,垂足为H.分别证得△BCH≌△ABP,可得CH=BP,BH=AP,结合CH∶BH=BP∶AP=1∶2,可得PH=CH,于是△PCH是等腰直角三角形,∠CPH=45°,所以PC平分∠EPF.
教学时注意关注学生不同的证明思路,但考虑到教学用时,每个小问用两种不同的方法证明之后,就及时往后推进,但要提醒学生还有更多的方法,可以课后进一步研究.
教学环节(三) 逆向探究 变式拓展
问题3:如图8,正方形ABCD中,以BC为直径作半圆O,以D为圆心,DA为半径作圆弧与半圆O交于点P.
(1) 连接DP,判断DP与圆O的位置关系,并说明理由;
(2) 射线CP交边AB于点E.求证:E为边AB的中点.
教学预设:如果学生解决第(1)问有困难,教师要提示学生反复审题,特别是“两个圆”的定义“一中同长”,如图9,想到连接OP,OD,由“边边边”证出△DCO≌△DPO,可解决∠DPO=∠DCO=90°,进一步由“连半径,证垂直”的切线判定经验可证出DP与圆O相切.
第(2)问有不同的思路,限于篇幅,这里只提供一种.由上一问△DCO≌△DPO,可以得到DO⊥CE,进而可证△DCO≌△CBE,得BE=CO,即可代换出E为边AB的中点.
教学环节(四) 归纳小结 研究展望
小结问题:本课从正方形的一个经典图形出发,解决了很多过去就见过的数学习题,哪道问题是你之前没有见过的?请在小组内举例交流,并说说你对哪道问题印象深刻?
课堂小结之后,给出以下拓展题,作为学生课后继续钻研的挑战作业.
1. (对“问题2”再拓展)如图10,正方形ABCD中,E,F分别是边BC,CD的中点,AE,BF相交于点P.连接CP并延长交AB于点Q,求证:AQ=2BQ.
设计意图:这是“问题2”中第(2)问的拓展追问,由已有进展“PC平分∠EPF”,可得PQ平分∠APB.根據三角形角平分线的“比例性质”,可得BQ∶AQ=BP∶AP=1∶2.
2. 如图11,在“问题3”两道圆弧相交于点P之后,直线BP,DP与正方形的边分别交于点M,N.
(1) 求证:M为AD中点;
(2) 当AN=9时,求BN的长.
设计意图:这里第(1)问可看成“问题3”第(2)问的拓展,如图12,可补出“射线CP交边AB于点E”,已有进展“E为边AB的中点”,结合“直径所对的圆周角是直角”得出∠CPB=90°,证出△BCE≌△ABM,可得AM=BE,再等量代换,可得M为AD中点;解决第(2)问时,仍然观察图12,将NP,NB看成是圆O的两条切线长,它们是相等的,这样在Rt△PEB中,可证得N为BE的中点,于是N为AB的四等分点,结合AN=9,则BN的长为3.
2 教学立意的进一步阐释
2.1 “一图一课”教学预设的关键在开放和留白
南京师范大学宁连华教授指出“教师在备课时应根据课型、教学内容、学生情况等因素对课堂留白进行预设.”本文关注的“一图一课”教学预设的关键在于开放和留白.具体来说,可以从正方形两边中点
的基本图形出发,在“问题1”中并没有急于安排学生训练相关习题,而是将问题设置成开放题,用开放题来驱动开放式教学,通过设问留白,全体学生的思维都被充分卷入“问题1”中,学生在独立思考一段时间之后,不同的学生有了不同的钻研进展与深度,然后小组内安排交流、分享,最后各小组选派代表全班交流展示.
2.2 “一图一课”学程导进要注意“快慢”平衡
宁连华教授曾指出:在设计教学内容时,应当注意“快与慢”的平衡.对于上文正方形专题课来说,显得尤为重要.比如,“问题1”是一道开放题,学生设计出一些简单的、浅层次的问题并不困难,但是要让学生深入下去,发现并提出“EP∶BP∶FP∶AP∶AE=1∶2∶3∶4∶5”这样深刻的性质并不容易,笔者曾多次试教该课,但能自主发现上述深刻性质的学生却很少,就要求我们在这个看似简单的开放问题教学环节要舍得花时间去等待,促进学生对基本图形深入思考、深刻理解.而在后续“问题2”“问题3”中面对一些较难问题时,只要有少数优秀学生能获得思路,就可尽快安排他们上台分享自己的解题思路,待他们讲解之后,再安排与这些学生数学能力相近或稍弱的学生进行复述(再讲一遍),以便让更多的学生跟进理解.
2.3 “一图一课”课堂小结要引导学生反思概括
专题课教学同样要重视课堂小结的精心预设.要通过小结环节引导学生学会回顾、反思和提炼本课所学内容,积累数学解题经验.涂荣豹教授在文[3]中认为:“解题学习中某些解题策略可以通过经验式概括而获得,共同特征是解決这类问题的具有一般意义的规律.”结合本文课例来看,我们在课堂小结环节预设了“小结问题”,让学生回顾本课解题过程中哪些是熟悉的问题,哪些是陌生的问题,对哪类问题印象深刻,并要求学生结合具体的题例在小组内交流.这里提出“讲题”的要求可有效促进学生深刻理解本课所学,因为在“听懂→会做→能讲”的学习进阶过程中,“能讲”往往包涵了前两者,也就达到了解题学习的最高阶.
参考文献:
[1] 蔡甜甜,刘国祥,宁连华.数学课堂留白艺术的理论探析与实践反思[J].数学教育学报,2018,27(6):2932.
[2] 于道洋,宁连华.试论数学教学中的“平衡”[J].中学数学杂志,2021(1):2830.
[3] 涂荣豹.数学学习中的概括[J].数学教育学报,2004,13(1):1722.
[4] 兰育哲.回顾促思 层层推进——“长方体和正方体”单元复习的思考[J].数学之友,2022,36(5):5253.
[5] 张文晴,曹佳慧,李香,李娅玲,王雪燕.新高考背景下江苏省数学试题变化分析[J].数学之友,2022,36(5):8385.
[6] 周凯悦,汤建钢.人教版与北师大版关于“线段、直线、射线”内容的比较研究[J].数学之友,2022,36(6):912.
[7] 李莹.课程思政视域下的高中数学教学设计研究——以高中数学“数列”教学为例[J].数学之友,2022,36(6):3538.
[8] 李春峰.探索化归思想在高中数学解题中的应用[J].数学之友,2022,36(6):5355.
[9] 张志刚.曲径通幽处:一道高考模拟题的背景揭示与破解[J].数学之友,2022,36(6):8084.
[10] 冯源,张晓贵.基于认知负荷理论的中学几何证明习题教学策略研究[J].数学之友,2022,36(1):24.

