基于多目标优化的微纳卫星群姿态控制

缪海斌, 刘鸿瑾, 吕权修, 邵立珍

1. 北京科技大学, 北京 100083 2. 北京控制工程研究所, 北京 100094

0 引 言

空间技术的发展已经过去半个多世纪,随着航天科学技术的进步,卫星的种类和功能也呈现出多元化的发展趋势,目前大量应用于通讯、导航定位、资源勘查及空间科学探测.而为了探索未知世界、进行新的科学研究以及观测新的现象,航天任务变得日益复杂,同时对卫星的姿态机动、跟踪与稳定控制的能力提出了更高的要求,传统的大卫星在一些方面已经不能满足任务的需要.微纳卫星具有研制周期短、成本低、响应快速、易于组网应用的显著特点,所以微纳卫星成为了卫星发展的热点,而且技术日趋成熟[1].虽然单个微纳卫星在性能上不如传统的大卫星,但是,微纳卫星群通过系统内个体之间的通信交流保证群内个体能够获取外界信息,使得整个微纳卫星群系统对环境的适应能力得到大幅度提升,从而能够完成极为复杂的太空任务[2].

微纳卫星控制的关键技术之一是姿态系统控制,设计有效的控制策略以实现对微纳卫星的姿态控制,已成为航天领域广泛关注的热门课题.对于卫星群姿态控制问题,主从控制方式较为成熟,目前很多卫星姿态控制的相关研究都是基于这一控制策略展开的,最早主从式控制策略出现在机器人编队控制中[3],随后WANG等[4]将该控制策略运用于卫星姿态中.与此同时,国内外其他专家也对主从方式的卫星编队展开了研究,文献[5-7]应用了反馈控制算法求解控制律用于卫星姿态控制;SUN等[8-10]针对存在输入约束和参数不确定性的卫星群姿态控制问题,研究了鲁棒控制在卫星群姿态控制中的应用;文献[11]中,提出了轨道LQR协同控制律方法,验证了存在干扰的情况下,从星相对主星姿态跟随的稳定性;文献[12]中,针对卫星群在飞行过程中转动惯量发生改变导致从卫星无法精确跟随的情况,提出了状态反馈非线性自适应控制方法;刘春生等[13]提出了一种将滑模控制理论与状态相关的黎卡提方程 (SDRE)相结合的鲁棒最优控制设计方法.这种方法首先考虑能耗性能指标,利用SDRE方法得到了飞行器姿态的最优控制律;然后将滑模控制理论与SDRE相结合,实现了飞行器姿态控制,并证明了系统的稳定性.上述方法大多数是传统的控制方法,没有考虑时间和能耗等性能指标,或者仅考虑了能耗这一单一性能指标,本文针对微纳卫星群姿态控制问题,以姿态误差函数和能耗函数作为2个性能指标函数,建立了其多目标优化模型.进一步采用弹性约束法求解2个性能指标函数的帕累托前沿,实现了微纳卫星群姿态机动控制和姿态协同控制,同时和文献[13]提出的基于SDRE的飞行器姿态最优鲁棒控制算法进行比较,验证了本文提出方法的有效性.

1 卫星姿态动力学和运动学模型

1.1 卫星姿态动力学模型

卫星的动力学模型由单刚体的欧拉动力学方程描述如下:

式中,u=[uxuyuz]T表示作用于刚体质心上的控制力矩,本文没有考虑干扰力矩,ω=[ωxωyωz]T为刚体的姿态角速度.

1.2 卫星姿态运动学模型

本文主要研究微小卫星群在小角度下的姿态控制,由于在小角度情况下[14],姿态角和角速度之间是准积分关系,为了简化控制系统设计,假设姿态角和角速度之间是简单的积分关系,即

其中:ω0为卫星轨道角速度,单位为rad/s;φ为滚角;θ为俯仰角;φ为航偏角,单位为rad.

令状态变量x=[φθφωxωyωz]T,可以将非线性系统状态变量x写成下式的形式

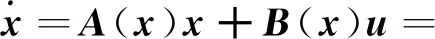
(1)

矩阵A和B都与状态系统有关.

2 卫星姿态控制中的优化问题模型

2.1 图论相关知识

本文考虑具有主从结构的卫星姿态控制问题.假设微纳卫星之间信息交换为有向的,即有向通讯拓扑[15].有向通讯拓扑图g由若干个顶点v和若干个边ε组成,顶点vi表示第i个卫星,i=0,1,…,m,其中v0为主星,边(vi,vj)表示卫星j能够获取卫星i的信息, 但并不能表示卫星i也可以获得卫星j的信息,此关系表明各卫星之间是单向联通的.定义A=[aij]∈Rm×m表示有向图的加权邻接矩阵,如果(vi,vj)∈ε, 则aij>0, 反之aij=0.一般情况下,假设顶点自身之间没有连通性,即aij=0.本文中假定主卫星不能获取从卫星的状态信息, 即(vi,v0)∉ε,∀i=1,2,…,m,并且仅有一部分从卫星可获取主卫星的状态,从卫星之间可以进行部分通讯.

2.2 欧拉法

为了建立上述2个问题的优化模型,本文首先将卫星姿态控制的连续时间系统通过常微分数值方法——欧拉法进行离散化,转换为离散系统,然后再建立多目标优化模型.

由于欧拉法算法简单,离散模型变量之间不存在耦合,计算量比较小,数字化实现比较容易,是一种简单实用的积分算法,本文采用欧拉法对式(1)进行离散化得到卫星姿态的离散模型为

(1)

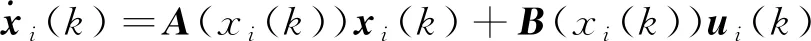
(2)

2.3 卫星姿态机动控制优化模型

在微纳卫星姿态控制控制过程中,不仅要考虑在最短时间内卫星达到期望的姿态,还要考虑能耗的问题.因为是体积很小的微纳卫星,自身携带的能量或者采集能量的装置就有限,如果不考虑能耗的问题,有可能在卫星没有达到期望姿态的情况下就因为能量耗尽导致任务失败.所以本文建立的多目标优化模型如下:

(3)

2.4 卫星姿态协同控制优化模型

微纳卫星群姿态协同控制过程中,因为没有目标姿态,卫星之间通过姿态信息传递使得所有的卫星姿态保持一致,本文希望所有卫星状态达到一致时,保持该时刻的姿态稳定运行,所以在优化目标函数中加入了角速度.本文建立的多目标优化模型如下:

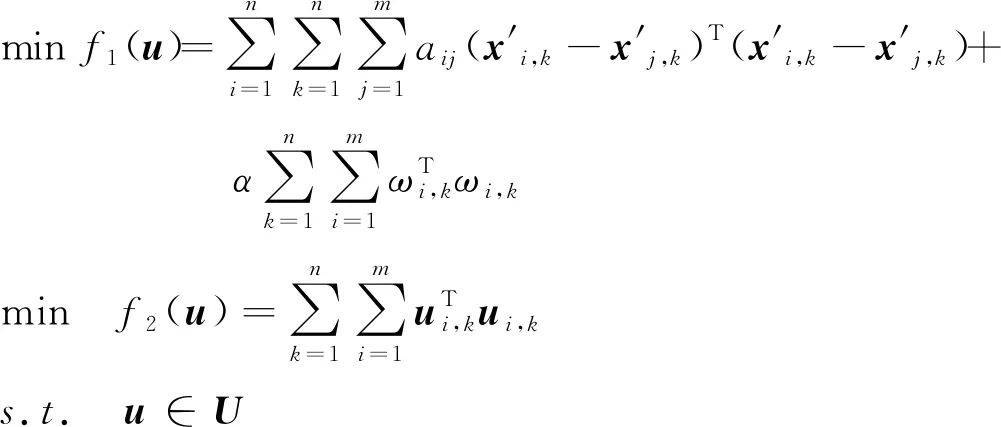
(4)

式中,ω=[ωxωyωz]T表示卫星的角速度,α是一个权重因子,其余参数的含义与式(3)相同.

2.5 多目标优化问题描述和弹性约束法

考虑具有如下p个目标,n个变量,m个约束的多目标优化问题(MOP).

minf(x)=[f1(x) …fp(x)]T

s.t.x∈X={x∈Rn:

g(x)=[g1(x)g2(x) …gm(x)]T≤0}

(5)

其中;X是变量空间Rn的可行域,为非空.目标空间Rp的可行域Y被定义为Y={f(x):x∈X}.

在弹性约束法中,将一个目标函数当作优化目标,其它目标函数当作约束条件,并将它们纳入模型的约束部分[16],如式(6)所示.图1是用弹性约束法求解2个目标函数得到的目标函数的可行域和在ε=3.7时弹性约束法求解得到的非支配点.

minf1(x)

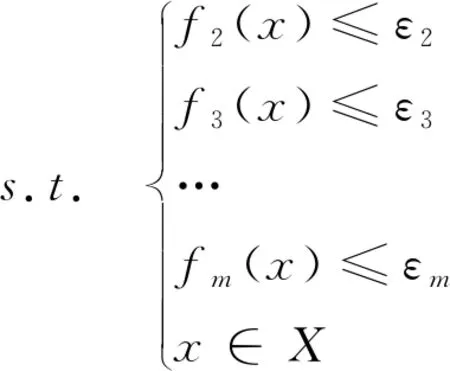
(6)

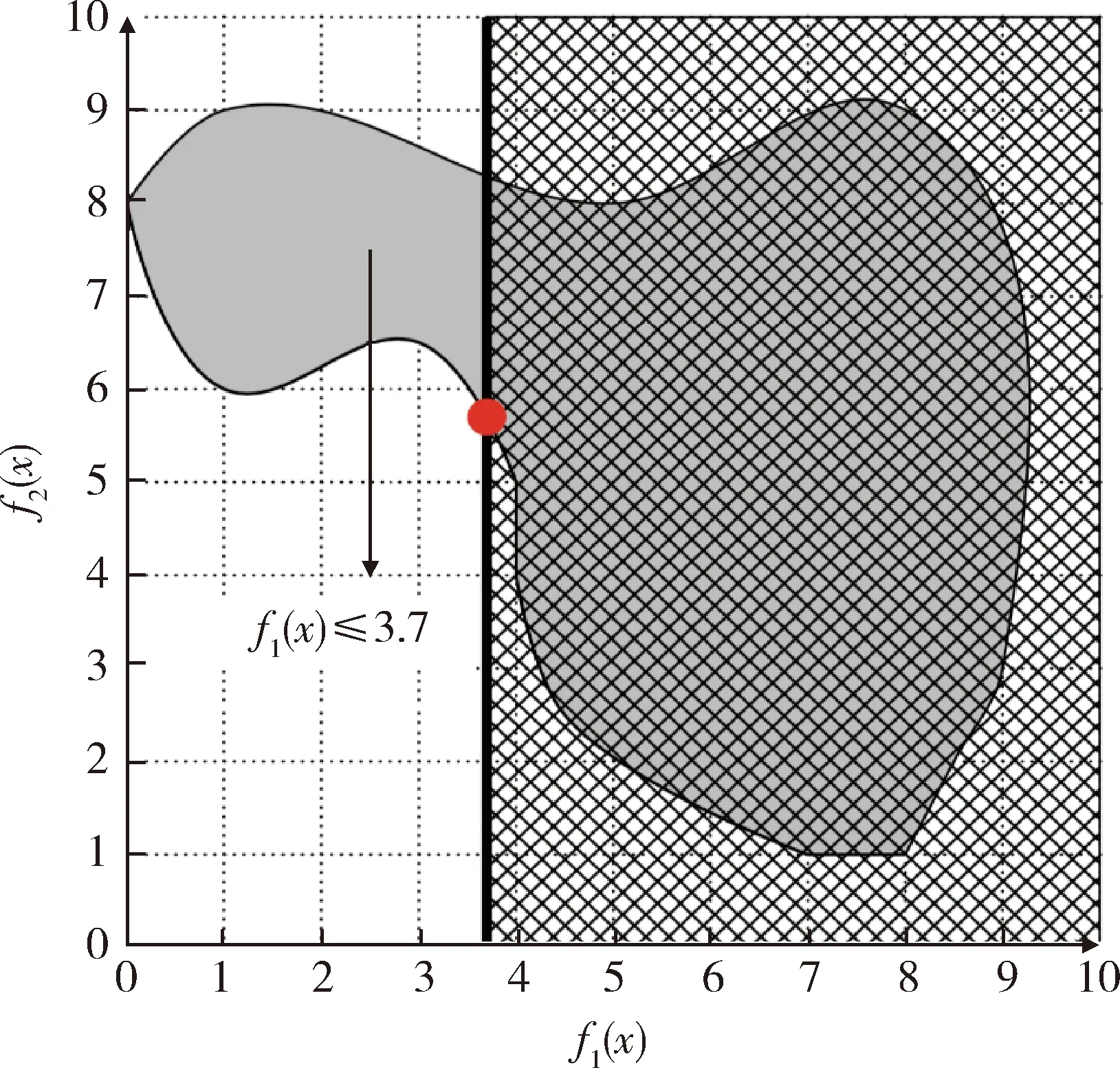
图1 弹性约束法示例图Fig.1 Example diagram of elastic constraint method

3 实验仿真

本节用图2表示微纳卫星群拓扑图来验证卫星姿态机动控制和卫星姿态协同控制,2个卫星姿态控制仿真中使用相同的拓扑图和初始值.如图所示,用0#表示主卫星,1#,2#,3#分别表示从卫星,只有1#卫星能接收到0#主卫星的信息,2#卫星只能接受到1#卫星的信息,3#卫星可以同时接受到1#卫星和2#卫星的信息.这些卫星通过求解其目标函数值时期最优,使得卫星群在最短的时间内达到目标姿态同时使能耗最小.

在仿真过程中,状态变量xi=[φθφωxωyωz]T,(i=0,1,2,3),节点的初始状态分别为x0(0)=[0.2 -0.2 0.1 0 0 0]T,x1(0)=[0.3 -0.1 0.1 0 0 0]T,x2(0)=[0.4 -0.2 -0.1 0 0 0]T,x3(0)=[0.32 0.2 -0.1 0 0 0]T.

转动惯量分别为Ix=0.004 kg·m2,Iy=0.005 kg·m2,Iz=0.006 kg ·m2,控制变量|ui|≤1.用欧拉法离散化过程中,取迭代步长h=0.01,总迭代步数为n=50,没有考虑干扰力矩.

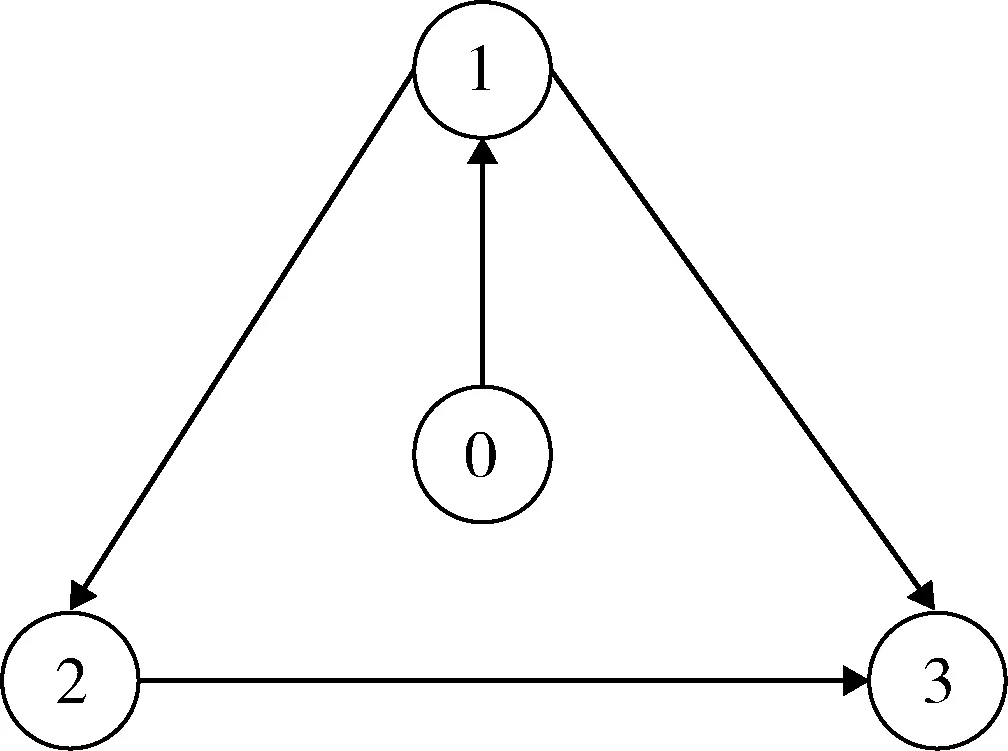
图2 卫星通信拓扑图Fig.2 Satellite communication topology

3.1 基于弹性约束法的帕累托最优解

本文中,目标函数由误差函数f1(u)和能耗函数f2(u)两部分组成,2个函数的表达式和前面优化模型中的一样,用弹性约束法求解帕累托前沿时,将误差函数f1(u)当作目标函数,能耗函数f2(u)加入约束条件,优化模型变为

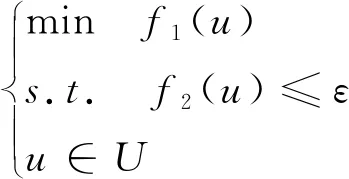
卫星姿态机动控制中,ε取值方式为ε=0.5:0.5:4.5,取9个不同的值,求解在能耗函数f2(u)小于不同ε的约束条件下的解u*,再计算在解u*下对应的2个单目标值f1(u*)、f2(u*),以f1(u*)为横坐标,f2(u*)为纵坐标绘制如图3.

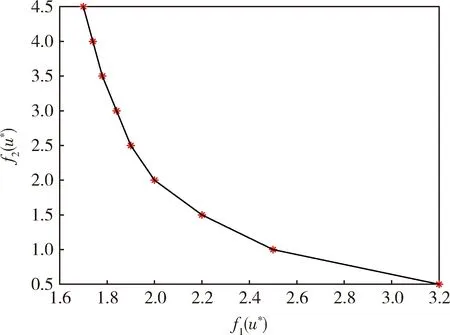
图3 基于卫星姿态机动制的帕累托前沿Fig.3 Pareto front based on satellite attitude maneuver control

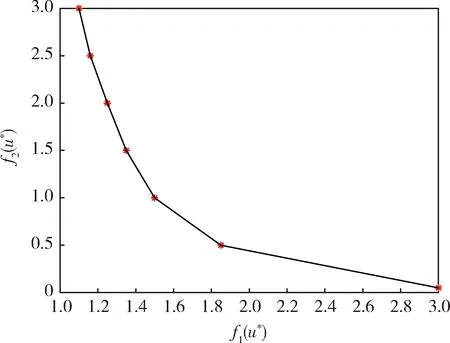
图4 基于卫星姿态协控同控制的帕累托前沿Fig.4 Pareto front based on satellite attitude coordination control

在卫星姿态协同控制中,ε取值方式为ε=0.5∶0.5∶3.0,最后取一个比零大的数0.05,求解的帕累托前沿如图4所示.其中,图3和图4是取不同的ε值得到的一组非支配点,然后用平滑的曲线连接这些点得到的帕累托前沿.图1是用弹性约束法求解多目标优化问题的一个示例图,图中的二维区域是2个目标函数的可行域,红色的点表示ε=3.7时用弹性约束法求解得到的非支配点.

3.2 卫星姿态机动控制仿真结果

在卫星群姿态机动控制仿真中,设定期望的姿态角为0,设ε=1.5和ε=3.从图5可以看出, 在ε=1.5时,迭代20步之后,所有的主卫星和从卫星都达到了期望的姿态,在ε=3时,从图6可以看出,在迭代到40步之后,所有的主卫星和从卫星的才达到期望的姿态.对比图5和图6,发现ε取值越大,需要迭代更多步以后才能达到期望的姿态,这是因为能耗函数值大,则误差函数就小,所以需要迭代更多的步才能收敛.图7和图8角速度轨迹曲线在迭代20步和迭代40步以后所有卫星的角速度都为零,达到了平衡状态,图9和图10表明所有的控制信号都被成功地限制在了预定的区间[-1,1]内,而且控制变量曲线变化比较平滑,是一种较为理想的状态.从图5和图6可以看出从主卫星到各个从卫星姿态角到达一致所用的时间越来越长.这是符合实际情况的,因为2#卫星和3#卫星只能接受1#卫星的信息而无法接受到0#卫星的信息,只有等1#卫星与主卫星姿态达到一致了之后,2#卫星才能实现与主卫星的同步.同样地,只有当1#卫星和 2#卫星与主卫星姿态达到一致后,3#卫星才可能与主卫星姿态一致.图11～13是用基于SDRE的飞行器姿态最优鲁棒控制得到的卫星姿态机动轨迹图,比较图5和图11,发现在迭代20步左右所有的卫星都达到了期望的姿态,但是可以发现本文所应用的优化方法使卫星从初始姿态到达目标姿态过程中运行轨迹更加平滑,说明卫星在飞行过程中姿态没有大幅度的变化,运行得更加平稳,可以减少卫星在飞行过程中由于姿态的大幅度变化而引起运行故障,体现了本文运用的多目标优化方法可以有效实现卫星姿态控制.

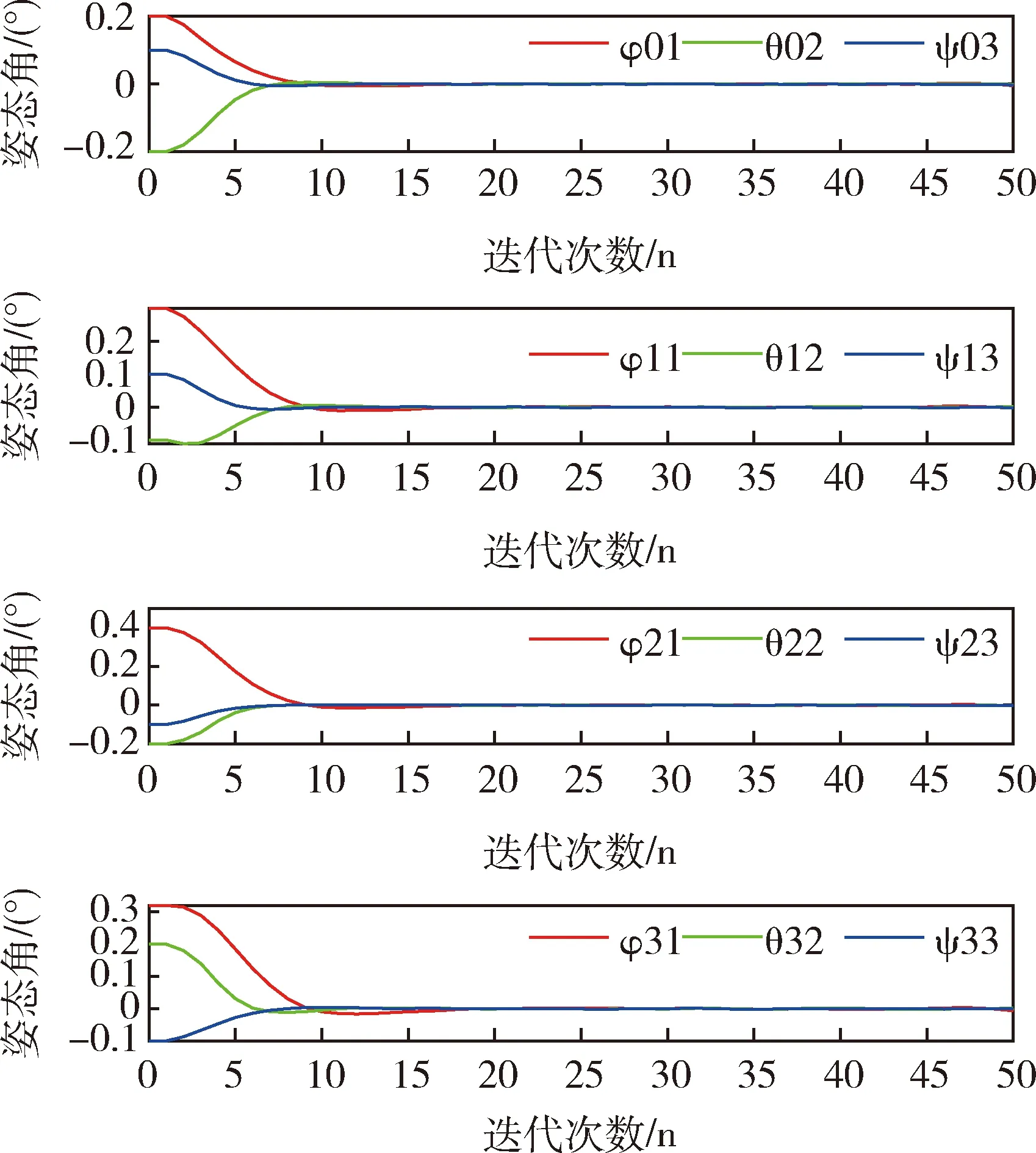
图5 ε=1.5时卫星角度轨迹图Fig.5 Satellite angle trajectories with ε=1.5

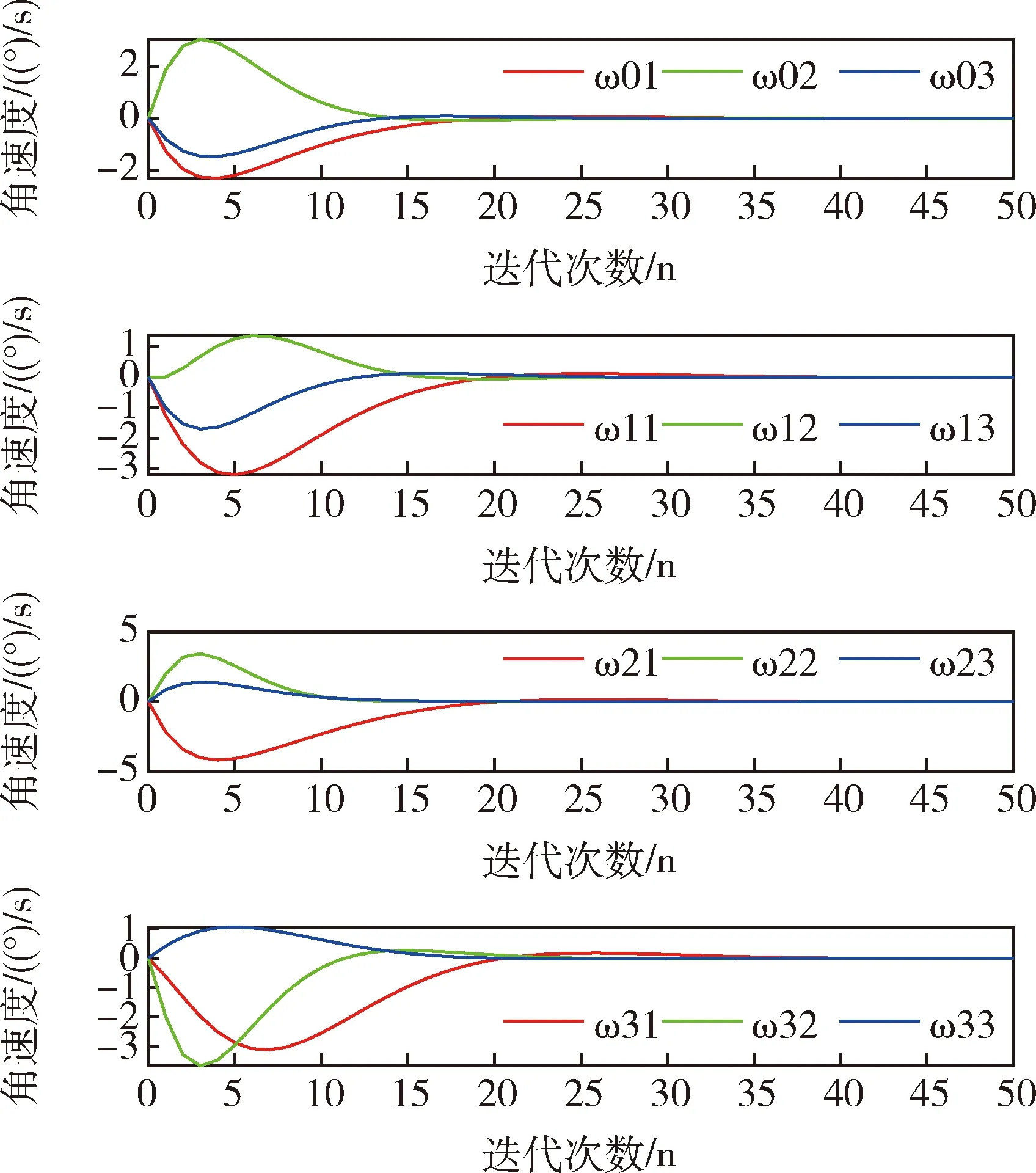
图6 ε=3时卫星角度轨迹图Fig.6 Satellite angle trajectories with ε=3

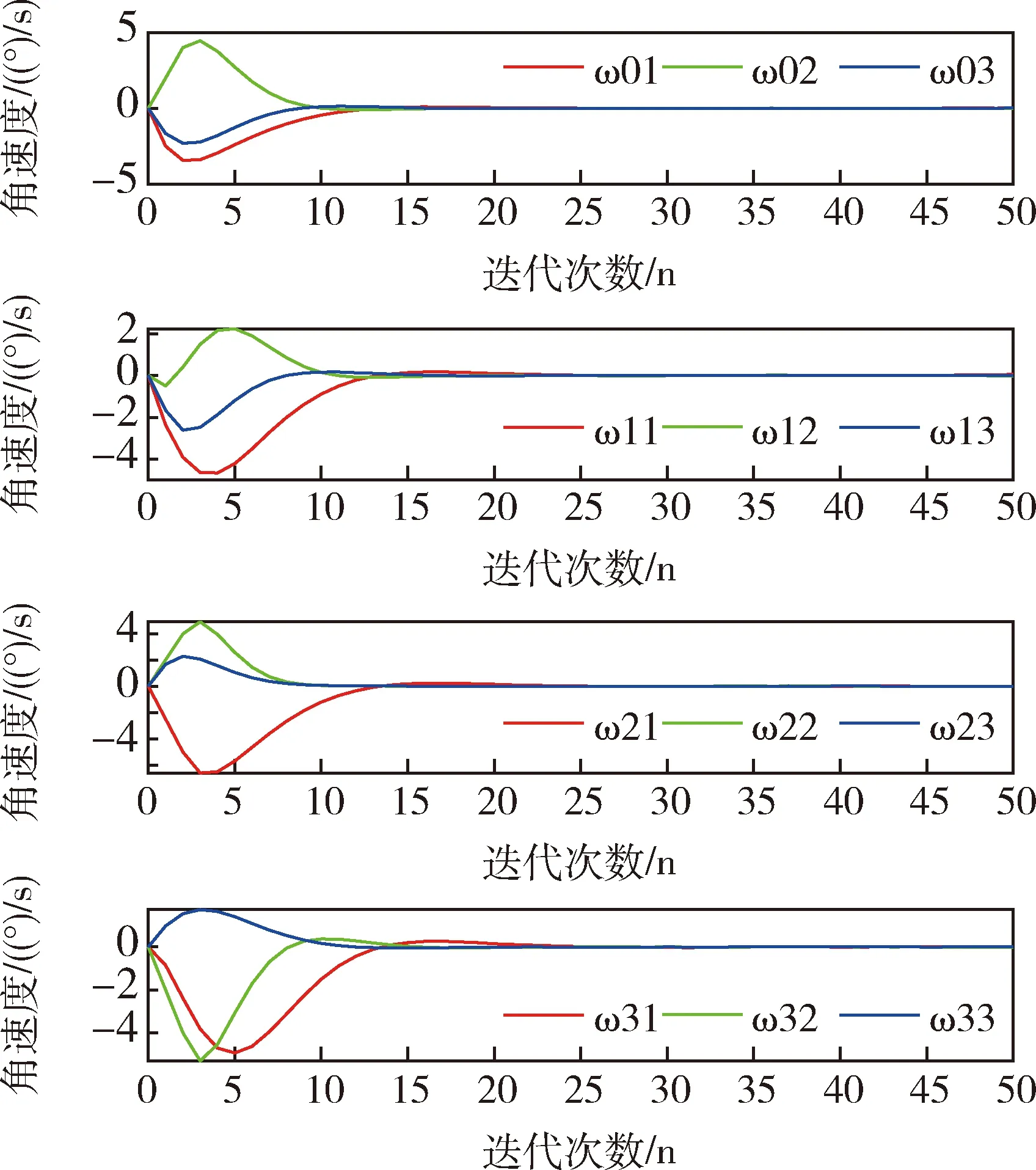
图7 ε=1.5时卫星角速度轨迹图Fig.7 Satellite angular velocity trajectories with ε=1.5

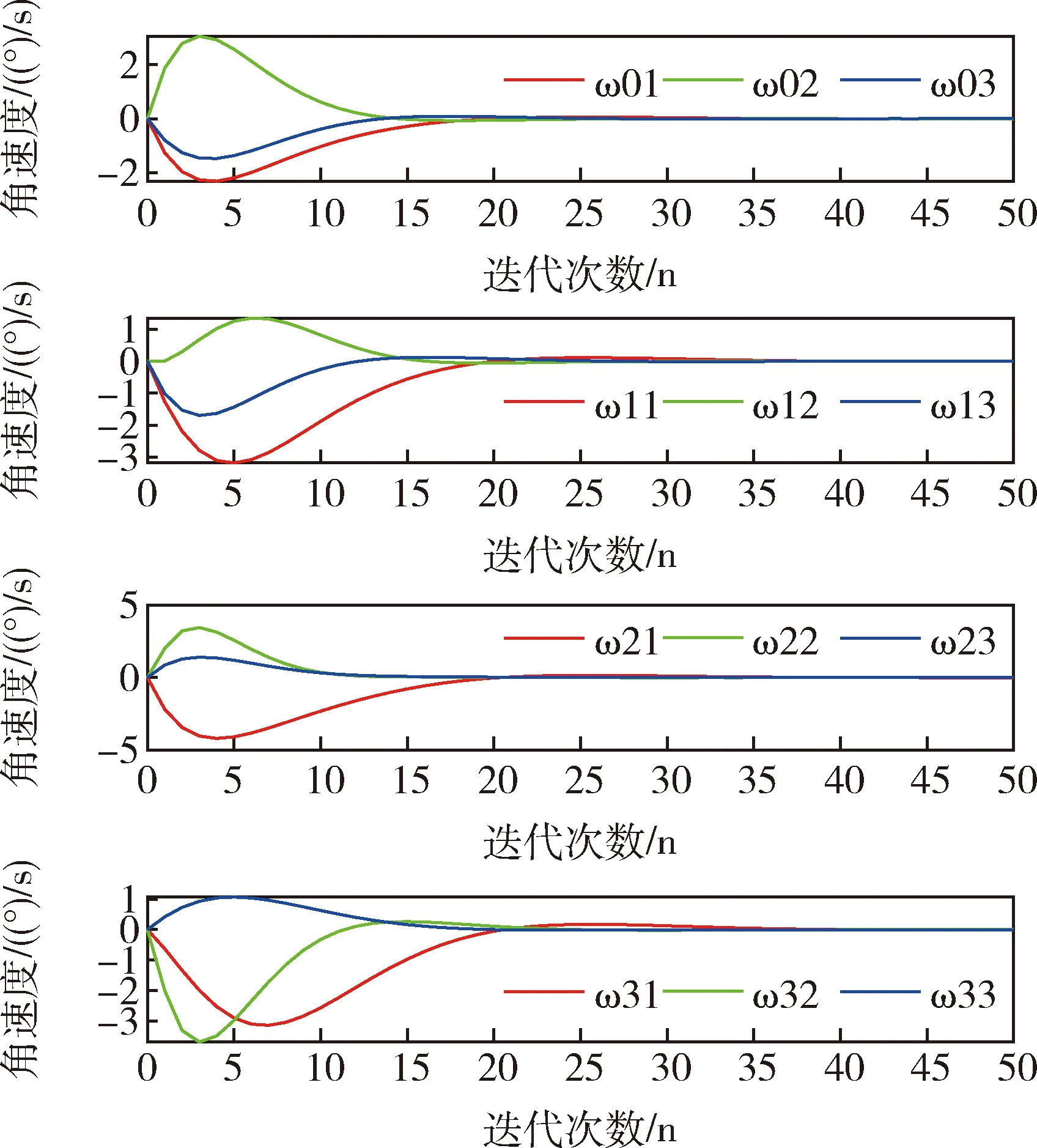
图8 ε=3时卫星角速度轨迹图Fig.8 Satellite angular velocity trajectories with ε=3

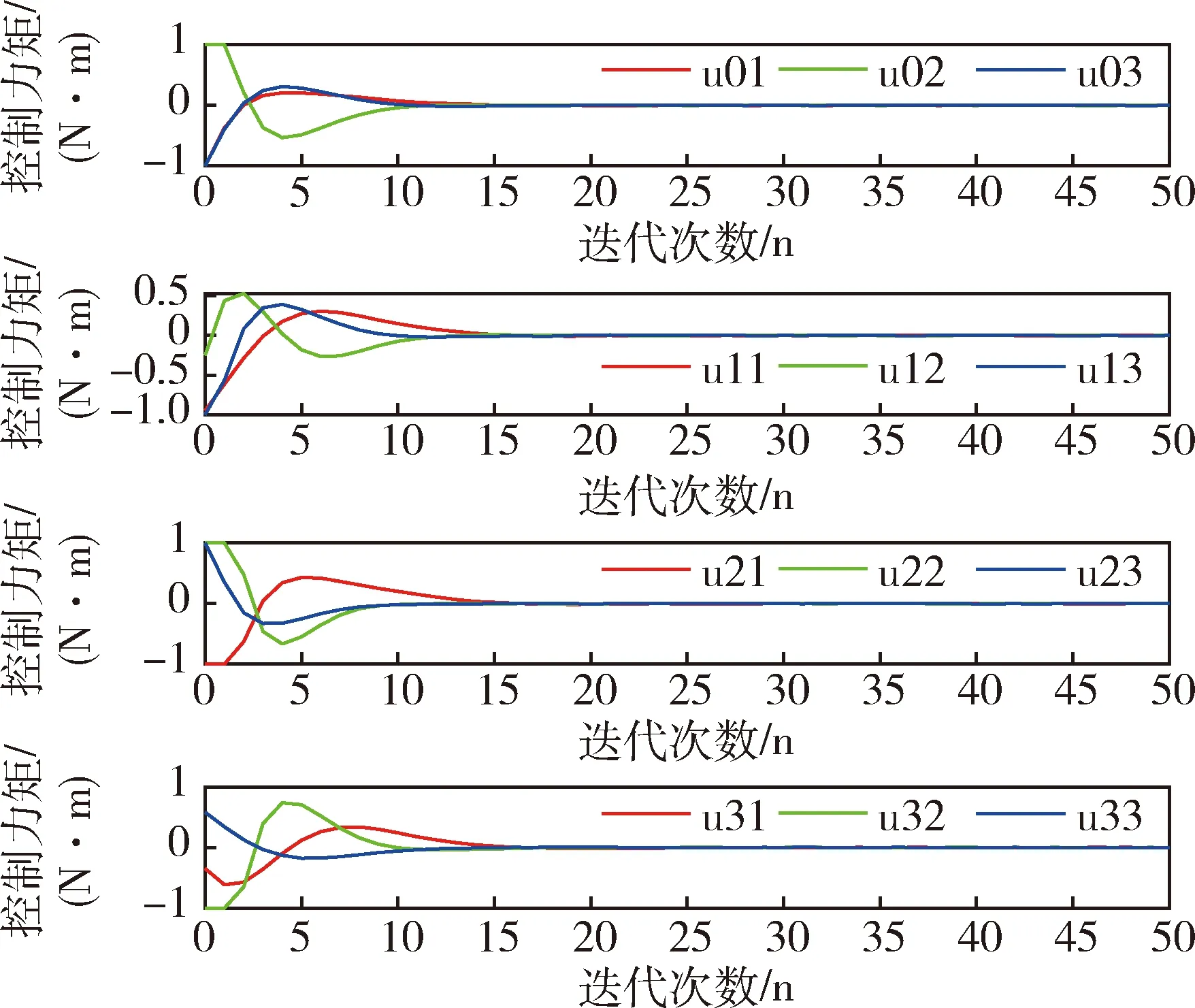
图9 ε=1.5时控制变量响应曲线Fig.9 Response curves of control variables with ε=1.5

图10 ε=3时控制变量响应曲线Fig.10 Response curves of control variables with ε=3

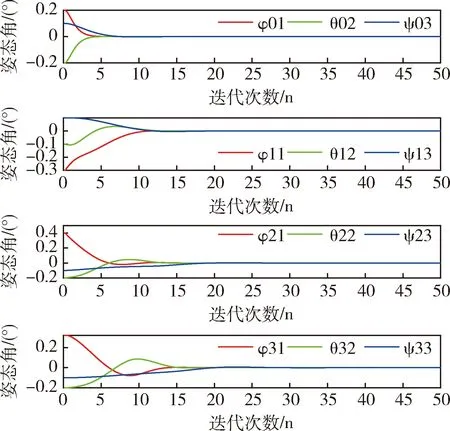
图11 基于SDRE姿态最优鲁棒控制的角度轨迹图Fig.11 Satellite angle trajectories based on SDRE attitude optimal robust control

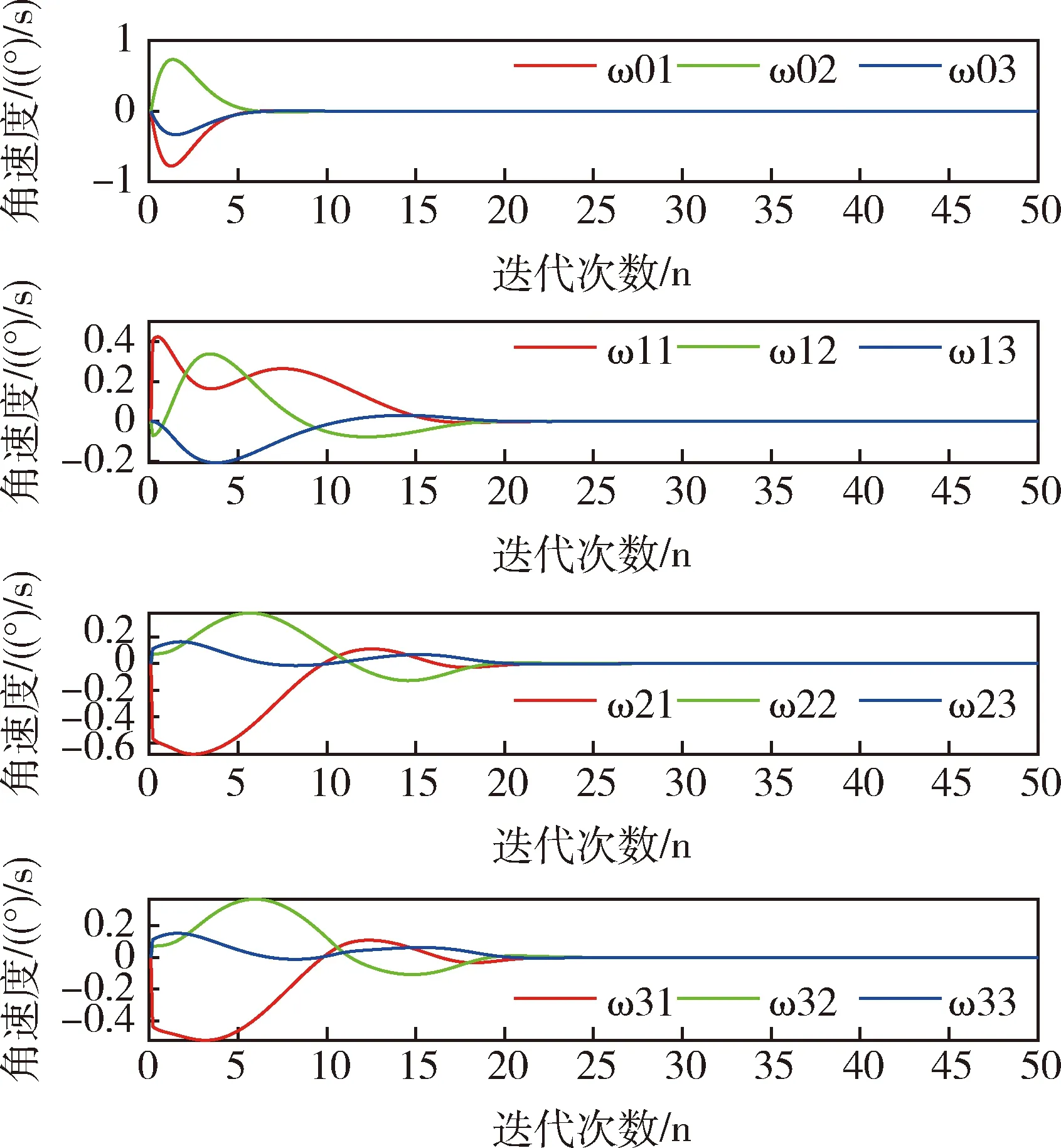
图12 基于SDRE姿态最优鲁棒控制的角速度轨迹图Fig.12 Satellite angular velocity trajectories based on SDRE attitude optimal robust control

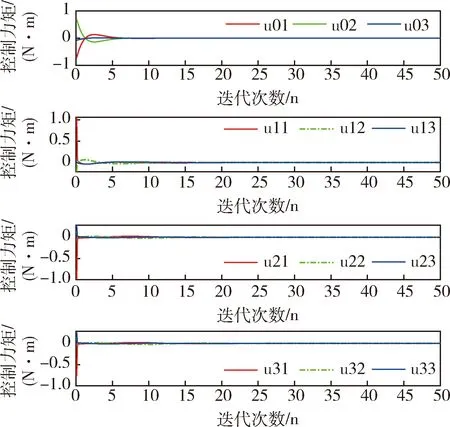
图13 基于SDRE最优控制的控制变量轨迹图Fig.13 Trajectories of control variables based on SDRE optimal control

3.3 卫星姿态协同控制仿真结果

在卫星姿态协同控制当中,初始状态的选取和卫星姿态机动控制中相同.通过反复实验,权重因子α取为0.01.本文同时优化2个目标函数,希望所有的卫星从不同的初始姿态开始在最短时间姿态达到一致.如图14所示,在ε=1时,迭代25步以后,所有卫星的滚动角、俯仰角和航偏角都达到一致,当ε=2时,结果如图15,需要迭代30步以后所有卫星的角度才能达到一致,在实际情况中,可以根据需要能耗小还是收敛速度快选择ε的值.图16～19表明所有卫星的控制力矩和角速度最后都达到了平衡状态,且状态轨迹图和控制力矩轨迹图都比较平滑,是一种比较理想的状态.

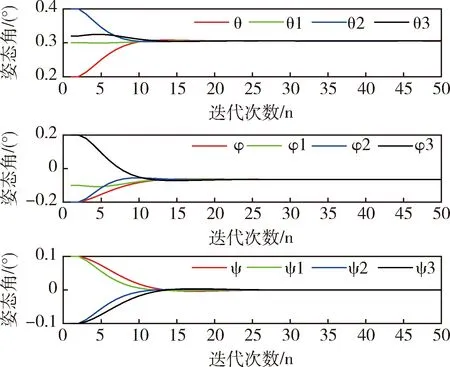
图14 ε=1时卫星角度轨迹图Fig.14 Satellite angle trajectories with ε=1

图15 ε=2时卫星角度轨迹图Fig.15 Satellite angle trajectories with ε=2

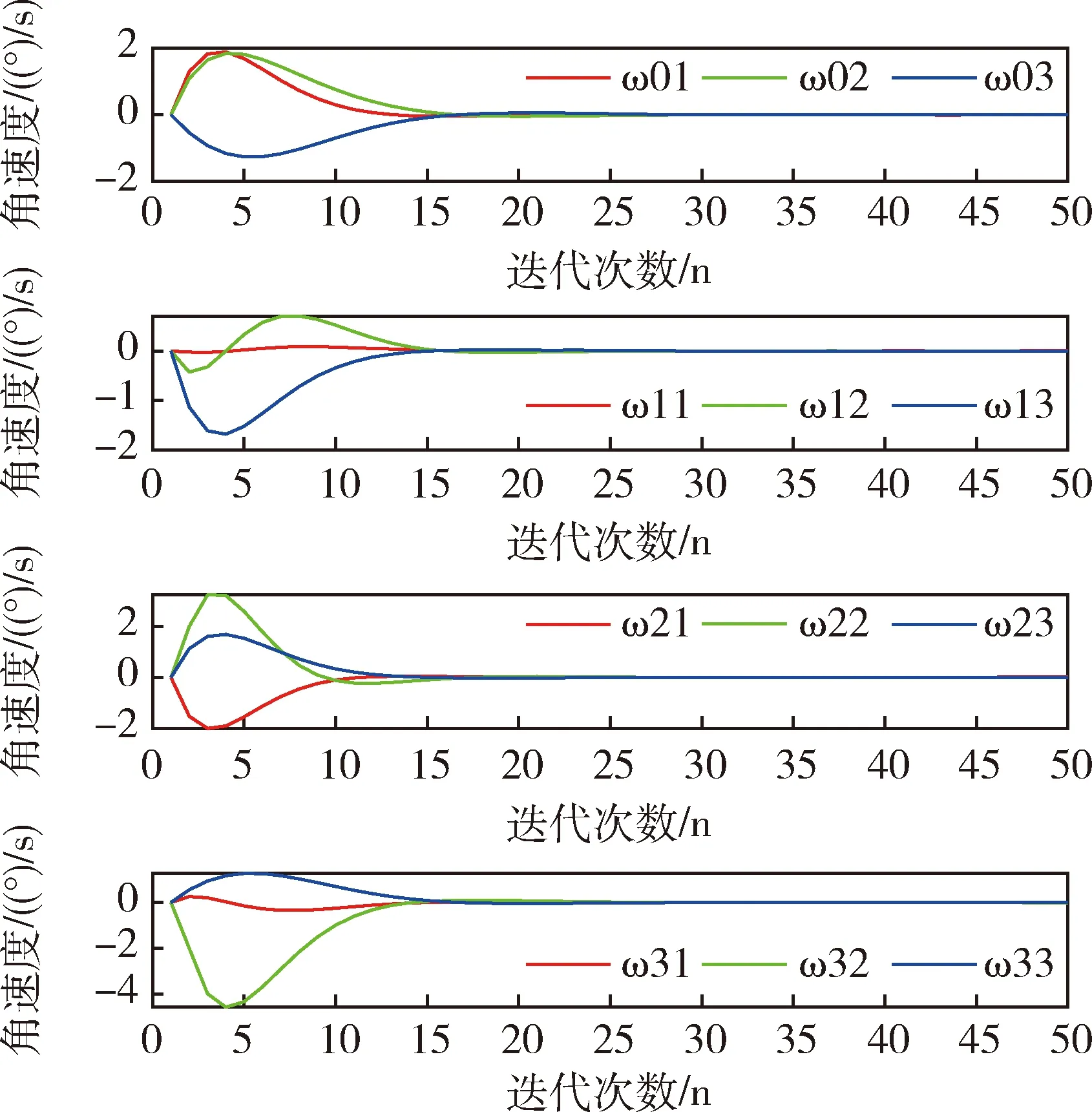
图16 ε=1时卫星角速度轨迹图Fig.16 Satellite angular velocity trajectories with ε=1

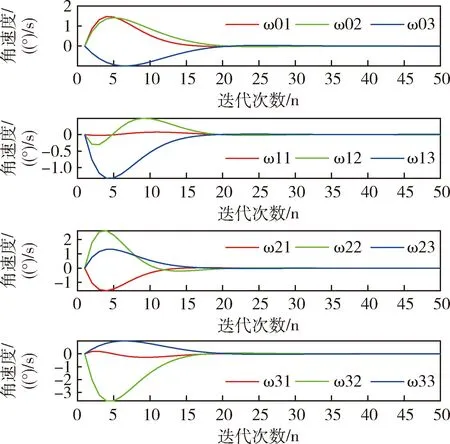
图17 ε=2时卫星角速度轨迹图Fig.17 Satellite angular velocity trajectories with ε=2

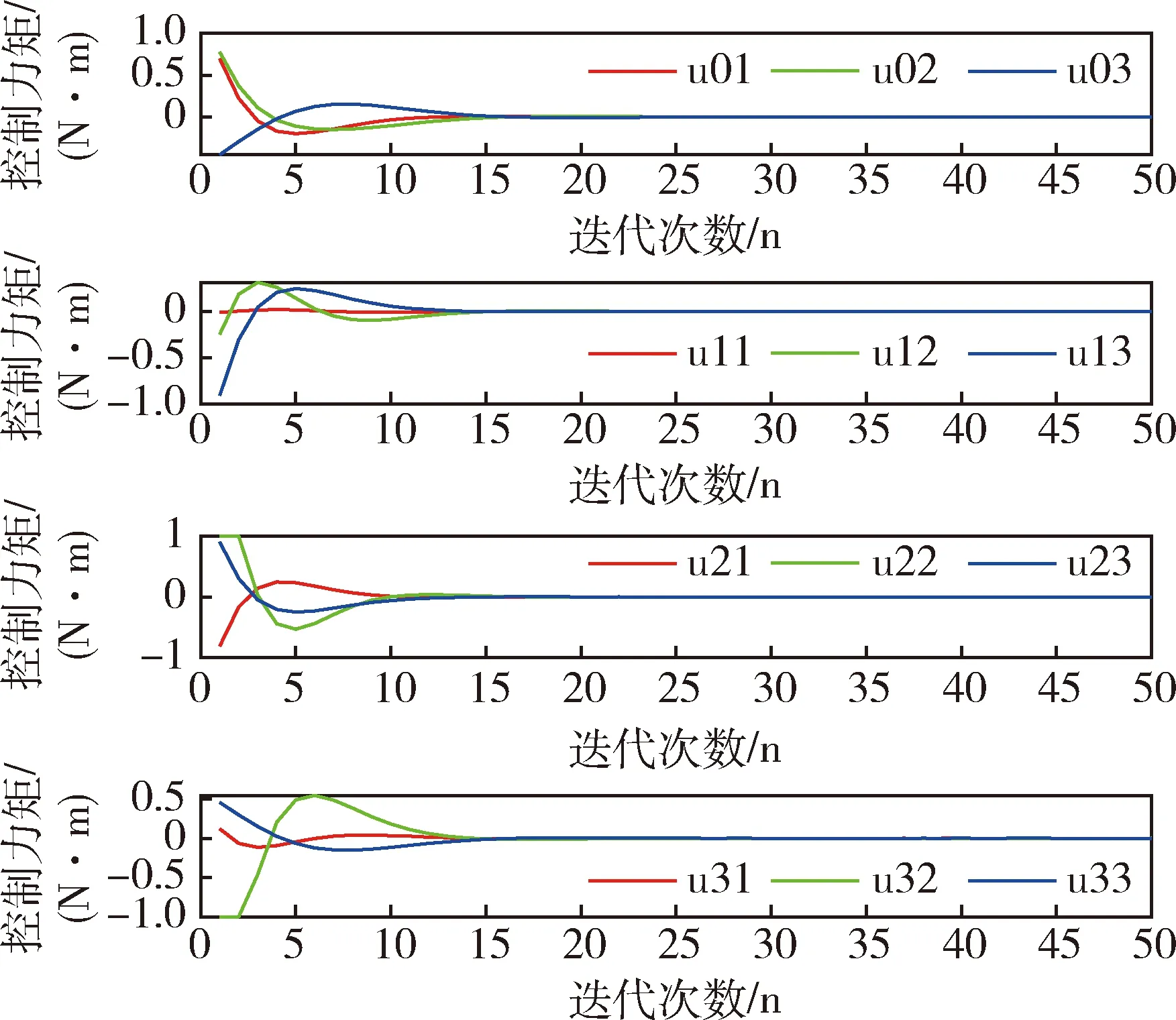
图18 ε=1时卫星控制变量响应曲线Fig.18 Response curves of satellite control variables with ε=1

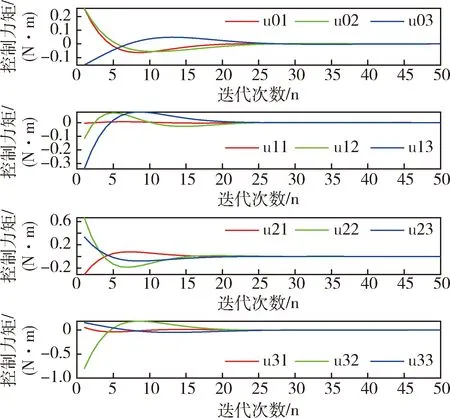
图19 ε=2时卫星控制变量响应曲线Fig.19 Response curves of satellite control variables with ε=2

4 结 论

本文基于卫星姿态机动控制和姿态协同问题,建立了微纳卫星群姿态控制问题的多目标优化模型,基于弹性约束法求解该多目标优化模型的帕累托前沿,取不同的值进行仿真,并和基于SDRE的飞行器姿态最优鲁棒控制算法进行仿真比较.仿真结果表明,对于微纳卫星群姿态机动控制和协同控制问题,用多目标优化算法可以很好地控制卫星群达到期望的目标姿态,并和基于SDRE的飞行器姿态最优鲁棒控制算法进行仿真比较,发现在相同时间内卫星群姿态都达到了期望的目标,说明本文运用的多目标优化方法可以有效实现卫星姿态控制.