挠性充液航天器复合自适应姿态机动控制
宋晓娟,李雪松,何晓东*,吕书锋
1. 内蒙古工业大学机械工程学院, 呼和浩特 010051 2. 内蒙古自治区特殊服役智能机器人重点实验室, 呼和浩特 010051 3. 内蒙古工业大学理学院, 呼和浩特 010051
0 引 言
随着航天技术的蓬勃发展,航天器携带的液体燃料相对于航天器总质量的比重相应增加,同时所携带的挠性附件也越来越大,对航天器的姿态控制以及稳定性造成了较大影响,在航天器的姿态机动过程中液体燃料的晃动和挠性附件的振动很有可能产生系统共振导致控制系统失效,甚至影响高精度的姿态机动任务,导致任务失败.因此一方面,在对航天器进行动力学建模时液体燃料的晃动以及挠性附件的振动变得越来越不可忽略,针对传统单一的刚体航天器或者刚-液耦合及刚-柔耦合的航天器设计的控制系统已经不能满足控制需要,刚-挠-液耦合的航天器动力学建模与控制问题已经成为航天领域的一个重要课题[1-3];另一方面,为尽量减小液体燃料晃动以及挠性附件振动对刚体航天器的耦合影响,提高航天器的稳定性,耦合航天器的控制系统在保证姿态稳定以及液体晃动和挠性附件振动稳定的前提下,如何尽量减小姿态机动时引起的液体晃动响应以及挠性附件的振动响应已经成为另一个重要课题[4-5].
迄今为止,国内外已有较多学者针对刚-液耦合航天器[6-8]和刚-挠耦合航天器[9-10]的姿态机动问题给出了多种控制策略,控制方法主要涉及传统的PID方法、自适应极点控制法、退步法、滑模控制法以及基于Lyapunov第二法的控制方法等[11-13].文献[14]采用变结构的控制方法设计了针对充液挠性航天器的姿态控制器,在满足姿态跟踪要求的同时有效减小了挠性附件的振动响应.文献[15]针对带液体晃动的月球着陆器,设计了一种基于无源性理论的控制方法对其进行姿态控制,有效抑制了液体的晃动.文献[16]针对液体多模态的充液航天器,设计了一种自适应动态反馈控制律与输入成型技术相结合的复合控制器,在保证航天器姿态机动稳定的同时有效地减小了液体的晃动作用.文献[17]采用饱和函数代替符号函数的滑模控制法对航天器的姿态进行控制,对于刚体航天器有效地减小了抖振,但是对于挠性航天器仍会触发持续的振动.
闭环控制方法通过系统输出或状态变量的反馈对系统进行稳定性控制,而大部分控制方法都含有一些固定的控制器参数,如经典的PID控制方法以及滑模控制方法等,若能将这些固定的控制器参数进行动态优化,设计为跟随系统改变的动态参数,则能有效提高控制系统的鲁棒性.有研究表明,采用自适应动态输出反馈控制策略可以对复杂的航天器达到较好的控制效果[18].文献[19]设计了一种动态滑模控制方法对挠性航天器进行姿态控制,在其中引入了动态切换函数,实现了对系统振动的抑制. 文献[20]用连续光滑的双曲正切函数代替符号函数设计了一种模糊滑模控制律,并在控制力矩中引入了滞后因子以避免由于起始控制力矩过大而引起的挠性附件的振动问题.
反馈控制方法对系统的参数和干扰有较强的鲁棒性,但是需要全状态信息反馈,而部分状态信息难以准确测量或有效利用,如无穷模态的挠性附件振动等.因此针对姿态机动时引起的液体晃动响应以及挠性附件的振动响应,前馈控制方法有更好的抑制效果.
本文将模糊控制技术和多模态输入成型技术与自适应输出反馈控制相结合,针对刚-挠-液耦合航天器的大角度姿态机动问题,设计了一种自适应输出反馈的复合控制方法.考虑航天器在进行大角度姿态机动的过程中会受到多种干扰力矩的影响且系统的各状态变量难以准确测量的情况,通过参数估计律估计系统各变量的真实状态,基于Lyapunov第二法设计了自适应状态反馈控制律对系统进行稳定性控制;采用模糊控制技术对控制律内的参数进行动态优化,加强控制律的鲁棒性;同时结合输入成型技术设计了多模态的输入成型前馈控制器,在保证系统姿态跟踪误差渐近收敛的情况下大幅度减小了姿态机动时的液体晃动位移以及挠性附件振动的位移响应.仿真结果验证了本文的有效性.
1 挠性充液航天器动力学建模
1.1 姿态运动学方程
航天器姿态运动学方程可表示为
(1)
G(ε0,ε)=[-ε,ε0I3-ε×]
(2)
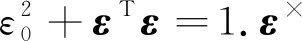
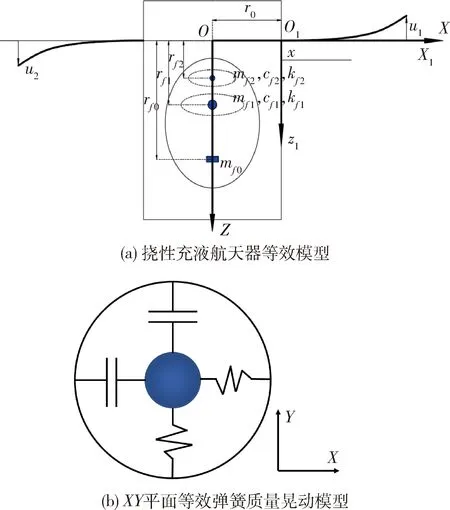
图1 挠性充液航天器动力学模型Fig.1 Dynamics model of liquid filled flexible spacecraft
1.2 挠性充液航天器动力学方程
航天器的模型如图1所示,OXYZ为航天器的本体坐标系,坐标原点O为航天器的质心.液体晃动等效为二阶弹簧质量模型,储液腔选取为椭球体腔,其中mf0、mf1、mf2分别为液体不晃动部分质量、液体一阶晃动部分质量和液体二阶晃动部分质量,等效液体各阶弹簧刚度为kfi,阻尼为cfi.平衡状态时各阶质量块距离质心的距离为bfi,晃动液体距离航天器质心的距离为rfi=[ηi1ηi2bfi]T,不晃动液体距离航天器质心的距离为rf0=[0 0bf0]T,ηi=[ηi1ηi20]T为液体晃动质量沿三轴的晃动位移.挠性附件等效为欧拉-伯努利梁,长均为l,单位密度为ρA,弯曲刚度为EI.本文只考虑航天器的姿态旋转运动,不考虑平动对航天器的影响.
航天器液体等效弹簧质量的动量矩可表示为
(3)


(4)
航天器总的动量矩可表示为
H=Jhubω+Hf+HP=Jω+hf+hp
(5)
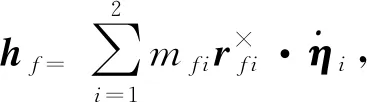
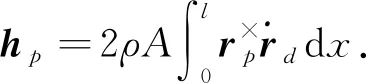
(6)
其中,Td为未知干扰力矩的总和,τ为控制力矩.
在旋转坐标系下,等效晃动液体的弹簧质量动量守恒,即可得到液体晃动的动力学方程为

略去式中的二阶以上小量并化简得
(7)
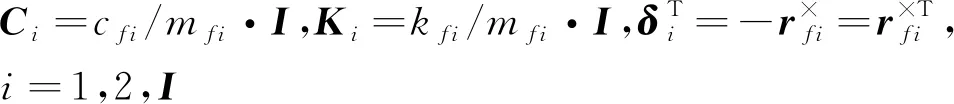
挠性附件的动力学方程由拉格朗日方程得到.附件的动能可表示为

(8)
不考虑重力势能的影响,只考虑弹性体变形能,挠性附件的势能为振动时产生的应变能
(9)

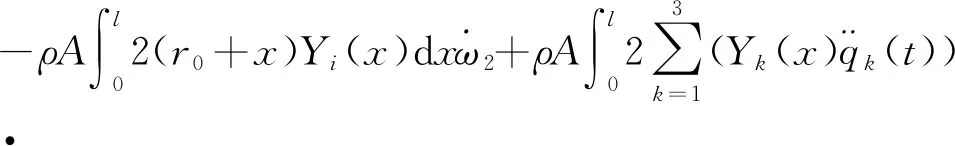
(10)
其中,qi为每一阶主振型的模态坐标,i=1,2,3.
考虑到主振型的正交性,同时略去二阶以上小量,上式可化简为
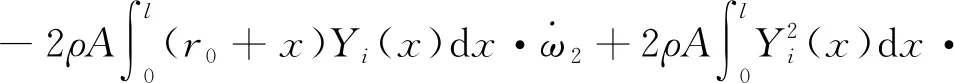
(11)
最终得到挠性附件的动力学方程
(12)

(13)
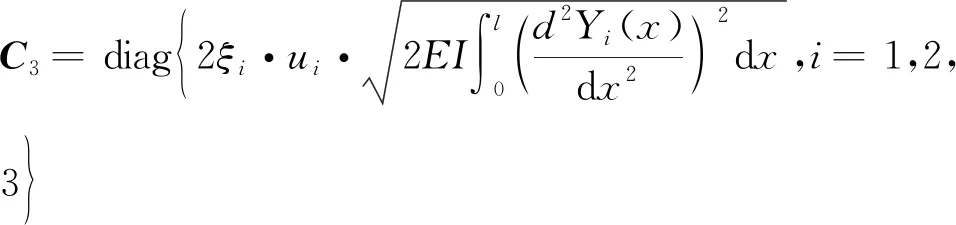
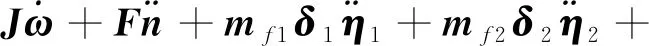
(14)
2 复合控制器设计
2.1 自适应输出反馈控制器设计
挠性充液航天器在进行大角度姿态机动过程中的姿态跟踪控制问题可描述为:在外部扰动力矩未知和系统状态变量不可测的情况下,设计自适应状态控制律τ,能够保证姿态跟踪误差渐近收敛.
首先确定航天器的控制系统.为控制方便,令
(15)
同时引入新的状态变量ψ、ζ,由系统的运动学方程可得到
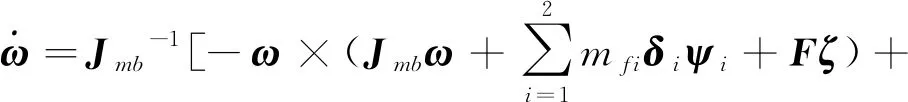
(16)
由此航天器的控制系统可表示为式(1)、式(15)和式(16).
假设1假设外部干扰力矩的总和Td具有连续性和一致有界性,其满足|Td|≤d.其中,d为沿着三轴航天器的3个惯性主轴关于|Td|的最大未知边界.

设计自适应输出反馈控制律为
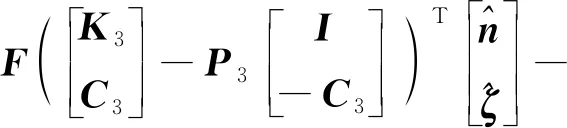
(17)
其中,Pi(i=1,2,3)为待设计的对称正定矩阵,εe=[εe1εe2εe3]T为指令四元数εc和实际四元数ε之间的误差,其定义为
(18)
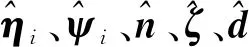
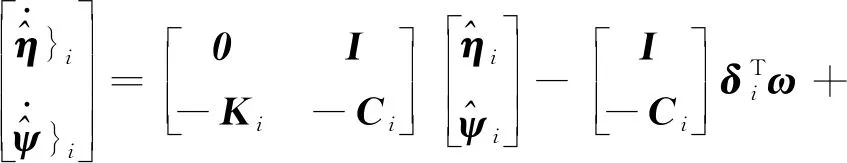
(19)

(20)

(21)
式中,Γ、P1、P2、P3均为对称正定矩阵,Pi(i=1,2,3)由如下Lyapunov方程确定,其中Qi为任意的对称正定矩阵.
(22)
定理1对于由式(1)、式(15)和式(16)组成的控制系统,控制律式(17)可使得闭环系统全局渐近稳定.
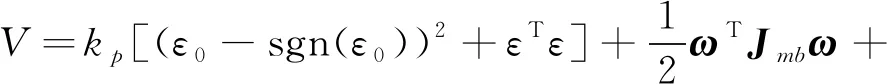
(23)
其中根据式(18)以及式(21)~(23)可知误差值的参数估计律为
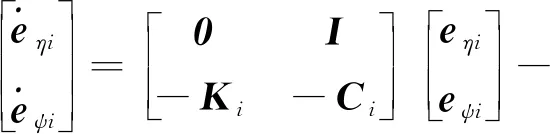
(24)
(25)
将式(23)沿着系统轨迹对时间求导并代入式(24)和式(25)可得
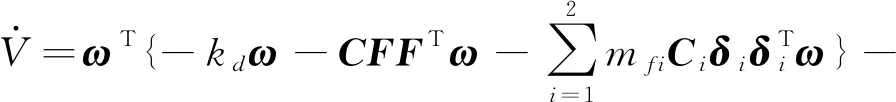
可见系统在Lyapunov意义下是稳定的.令

(26)


(27)
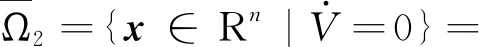
(28)
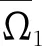
2.2 自适应输出反馈控制器模糊化参数设计
考虑到输出反馈控制律中kp和kd的参数是固定的,不适用于非线性的、参数时变的控制系统,因此采用模糊控制分别对kp和kd的参数选取进行模糊化动态优化,改善系统内各状态变量的抖振响应,提高控制律的鲁棒性.
优化后的控制力矩应平稳变化,且幅值较小,使得系统姿态四元数的响应以及角速度的响应更加平稳、波动更小且稳定速度更快.同时考虑到在姿态机动的初始时刻控制力矩过大会更易引起航天器内液体燃料的晃动以及柔性附件的振动,因此应尽量减小初始时刻的控制力矩.
为度量系统内各状态变量相对于平衡位置的平稳性,取误差四元数和角速度的绝对值作为模糊控制器的动态输入,设计如下模糊规则:
为了不断优化和完善数值模式的中小尺度预报能力,需要对微物理参数化方案进行对比研究,以便找到影响某一区域强降水过程预报能力的主要微物理过程。因此本文利用中尺度WRF数值模式,分别采用Morrison和Milbrandt-Yau双参微物理方案对辽宁省的一次强降水过程进行数值模拟,通过对地表累积降水量、降水强度和云中微物理量以及微物理过程的分析,对比研究了以上两种双参云微物理方案对强降水的预报效果,并找到降水预报差异的具体云微物理过程。
初始时刻误差四元数较大,kp应较小以减小控制力矩来减小抖振,同时角速度越大,kd越大,但增速越小以提高系统平稳性;随着误差四元数的减小kp应增大以加快系统响应,同时角速度越大,kd越小;当系统接近稳定时误差四元数接近于零,此时kp随着角速度的增大而减小以减小控制力矩来降低系统的抖振,同时kd随着角速度的增大而减小.
输出变量分别为kp的变化量Δkp以及kd的变化量Δkd.对输出变量Δkp和Δkd分别编写25条模糊规则,最后采用重心法去模糊化,得到Δkp以及Δkd的精确值.优化后的kp以及kd值为
2.3 多模态输入成型前馈控制器设计
前两小节提出的自适应输出反馈模糊控制器能够保证系统的姿态跟踪误差渐近收敛,但是在姿态机动的过程中液体燃料的晃动作用以及挠性附件的振动作用较大,为保证液体燃料的晃动位移以及挠性附件的振动位移在系统稳定之前尽可能的小,设计了基于输入成型技术的前馈控制器对其进行抑制.
输入成型技术是一种广泛应用于振动抑制的前馈控制技术. 不同于闭环控制方法需要状态变量的反馈进行控制,输入成型技术通过对输入指令卷积一系列不同幅值和时滞的脉冲序列来改变输入信号,从而得到预期的输出响应,使系统在完成预期刚体运动的同时不引起或只引起可接受的原始指令带来的振动.输入成型技术的关键在于一系列脉冲序列即输入成型器的设计.对于一个典型的二阶系统,其对单个幅值为Ai,时滞为ti的脉冲的响应为
(29)
式中,ω是系统的自然频率,ζ为系统的阻尼系数.该系统对多个脉冲序列的响应为
(30)
为了使系统在多个脉冲作用下的响应抵消为0,令上述响应的幅值为0,即需要满足
(31)
(32)
为使整形的时间最短,可令t1=0,同时为使系统达到原输出点,令脉冲序列的幅值和为1,由此可得到最简单的两脉冲ZV输入成型器,其脉冲的作用时间和幅值为
(33)
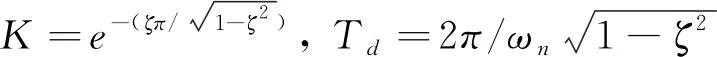
对于多阶模态的系统,输入成型器可由每阶模态的输入成形器进行卷积得到
Amult=Am1*Am2…*Amn
(34)
其中,*代表卷积运算,Ami代表第i阶模态的输入成型器的幅值.
由系统内液体的晃动方程(14b)、(14c)以及挠性附件的振动方程(14d)可知,系统内液体和挠性体的振动均为典型的二阶振动系统
(35)
其输入部分f(t)均为系统角速度导数的耦合项.将系统角速度导数的表达式(16a)以及控制力矩的表达式(17)代入液体和挠性体的振动方程式(14)中,可见所有振动方程的输入均为四元数和系统状态变量的函数,因此选取姿态机动的指令四元数作为指令输入对系统进行输入成型的前馈控制.
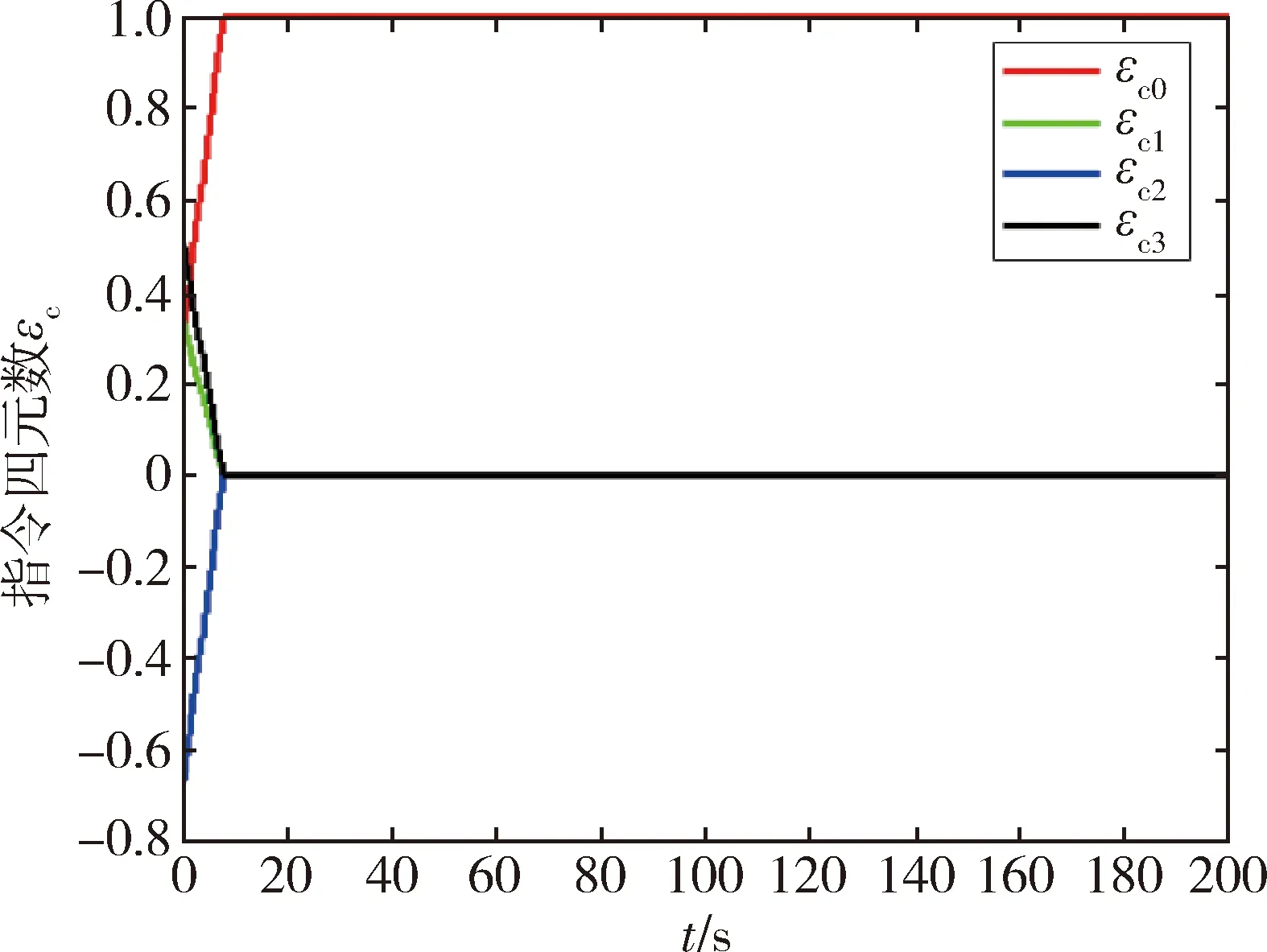
图2 输入成型后的指令四元数Fig.2 Command quaternion after input shaping
3 数值仿真
选取刚体航天器的转动惯量为
液体等效模型的相关参数为
mf0=50.92 kg,mf1=20 kg,mf2=0.8 kg,cf1=3.334 N·s/m,kf1=55.21 N/m,bf1=1.127 m,cf2=0.237 N·s/m,kf2=7.27 N/m,bf2=0.994 m,bf0=1.137m.
挠性附件的相关参数为
l=3 m,r0=0.65 m,E=7×1010N/m2,I=3×10-9m2,ρ=2.8×103kg/m3,A=1.125×10-2m2.各阶模态的阻尼系数为ξ1=0.01,ξ2=0.007,ξ3=0.005.
自适应输出反馈控制器的参数为
kp=90,kd=600,λ=0.1,Γ=0.1I3.
模糊控制器的参数为
kp1、kp2的模糊增益为30,kp3的模糊增益为45,kd1、kd2的模糊增益为350,kd3的模糊增益为500.
正定矩阵P1、P2、P3选取为
P1=diag{55.2, 55.2, 1, 80, 80, 1},
P2=diag{10, 7.27, 1, 70, 70, 1},
P3=diag{0.1, 3.94, 30.92, 10, 10, 20}.
用于分别得出上述Pi值的对称正定矩阵Qi可由式(22)反推得到.假设航天器所受外部干扰力矩的集总扰动为

自适应输出反馈复合控制器的仿真结果如图6~8所示. 其中图3~8分别给出了3种控制器的控制力矩响应、角速度响应以及姿态四元数响应的对比图. 红色实线为式(17)的基础控制律得到的仿真结果;蓝色虚线为加了模糊控制后的仿真结果;黑色点划线为加了模糊控制以及前馈控制之后的复合控制器的仿真结果.
由结果可见基础控制律可使系统在110 s左右进入渐近稳定状态,但初始控制力矩较大;模糊控制器减小了控制力矩的整体幅值,减小了初始力矩的大小,使控制力矩变化得更加平稳,也因此使得系统角速度以及姿态四元数的响应变化得更加平稳,可见模糊控制器能够对控制力矩的参数kp和kd进行有效地优化,改善角速度以及姿态四元数的响应,使系统获得更好的控制效果;同时可见加了多模态输入成型技术的复合控制器会使系统的稳定产生一定的延迟,但对比于模糊控制器,系统角速度以及控制力矩的变化幅度变得更加缓和. 控制力矩从0开始缓慢变化,且达到的最大幅值也更小,最大限度地减小了航天器在姿态机动的初期因控制力矩过大引起的系统抖动.可见复合控制器能够使航天器的姿态机动变化得更加平滑,更加稳定. 仿真结果验证了3种控制器的有效性.
图6~8给出了前两阶液体晃动以及前三阶挠性附件振动的位移响应图.由仿真结果可以看出液体晃动及挠性振动的响应在50 s左右趋近于稳定,虽然模糊控制器能有效地减小系统姿态机动时导致的液体晃动位移以及挠性附件的振动位移,但是减小的幅值不大;而加入多模态输入成型的前馈控制器后,液体晃动以及挠性附件的位移响应大幅度减小,可见多模态输入成型前馈控制器对姿态机动时产生的液体晃动以及挠性附件的位移响应的抑制效果较为明显.
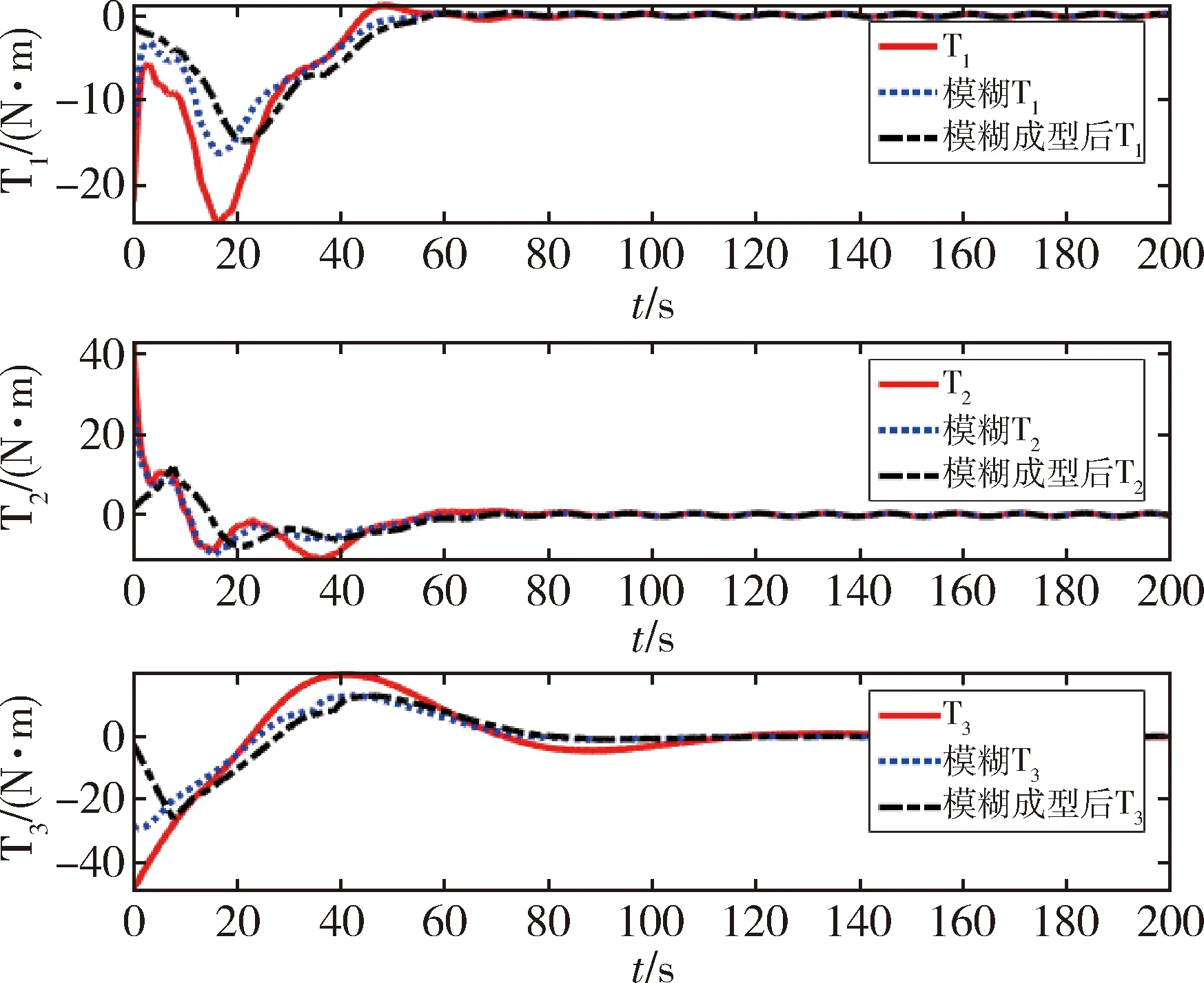
图3 控制力矩响应Fig.3 Control torque responses
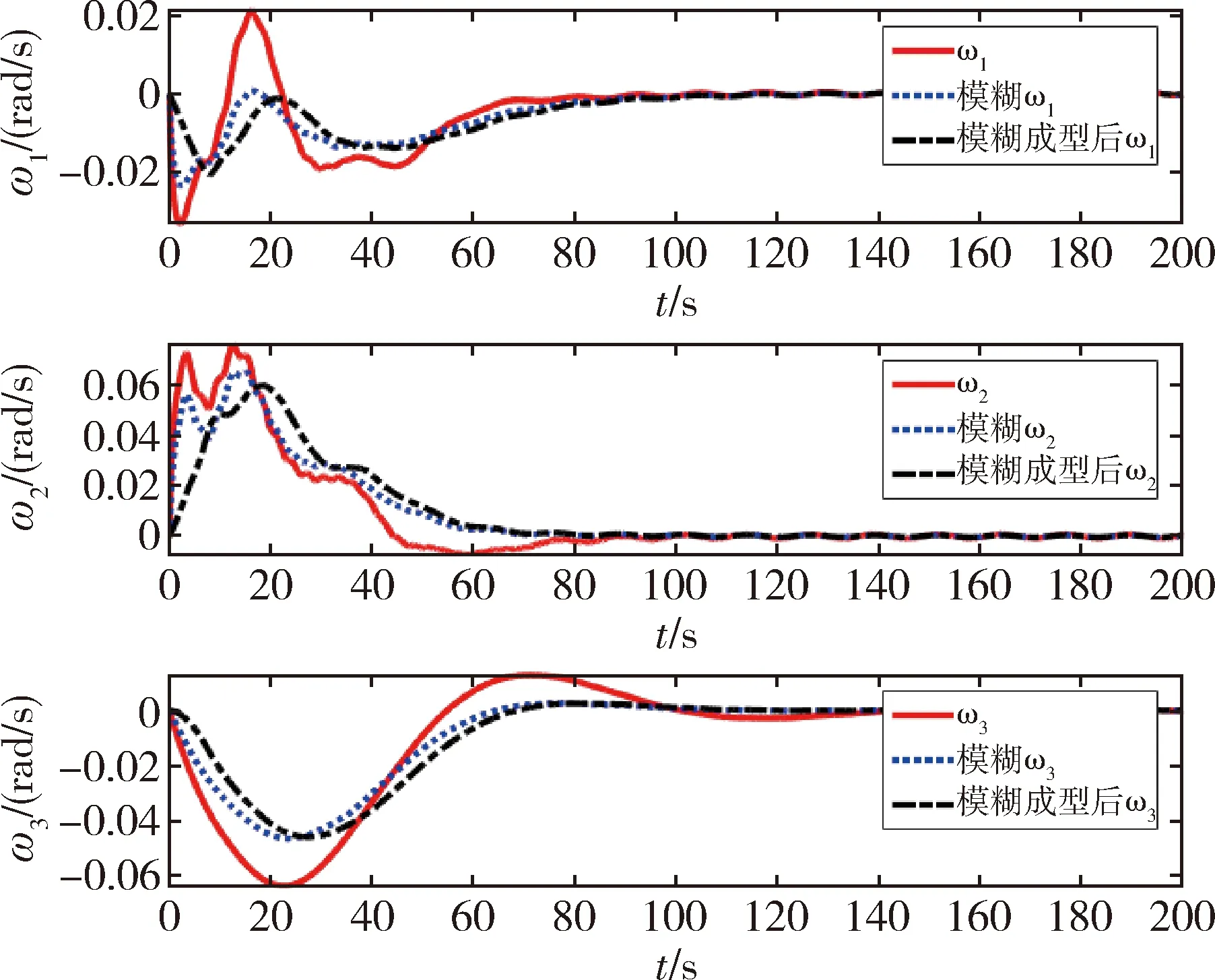
图4 姿态角速度响应Fig.4 Attitude angular velocity responses
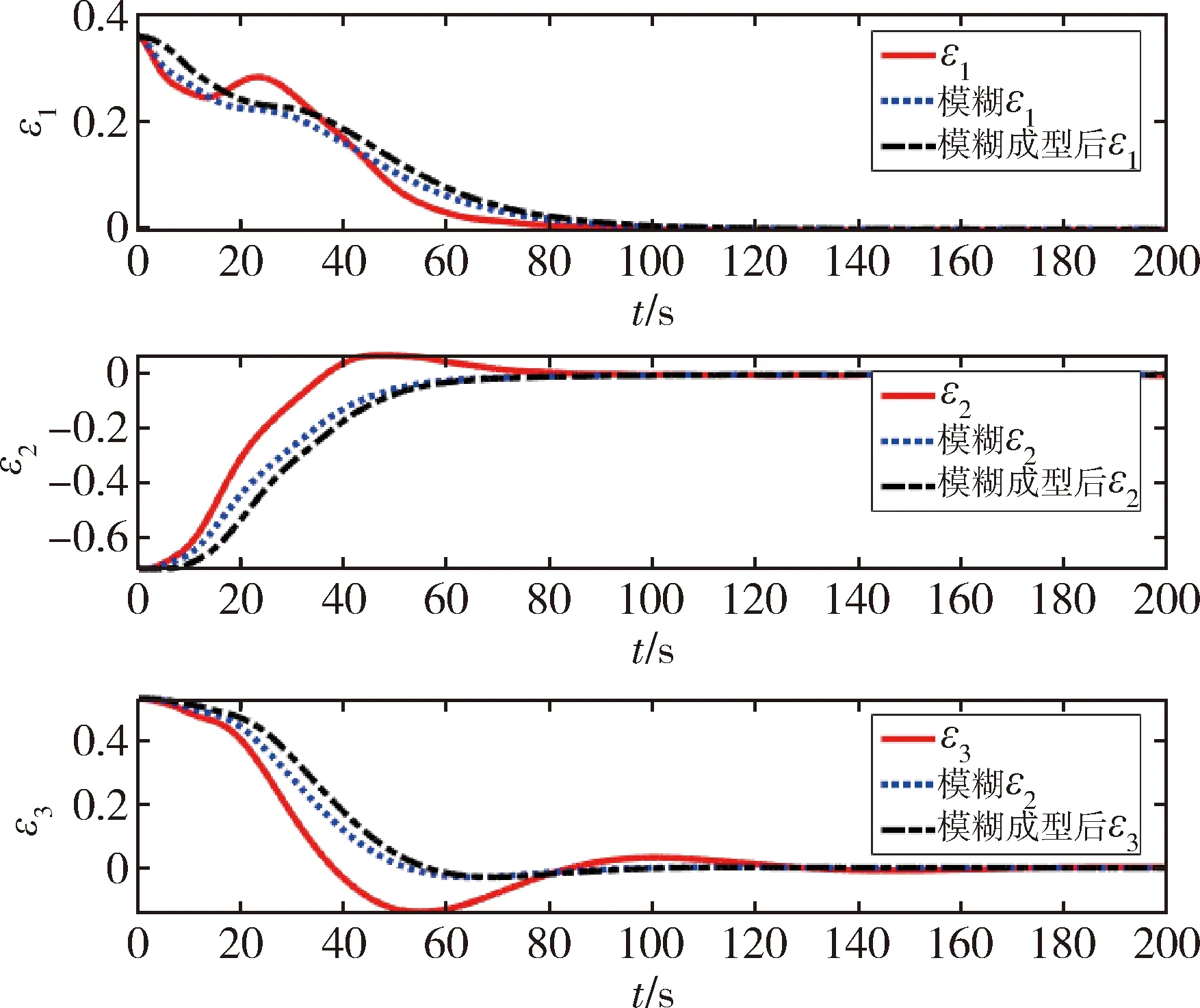
图5 姿态四元数响应Fig.5 Attitude quaternion responses
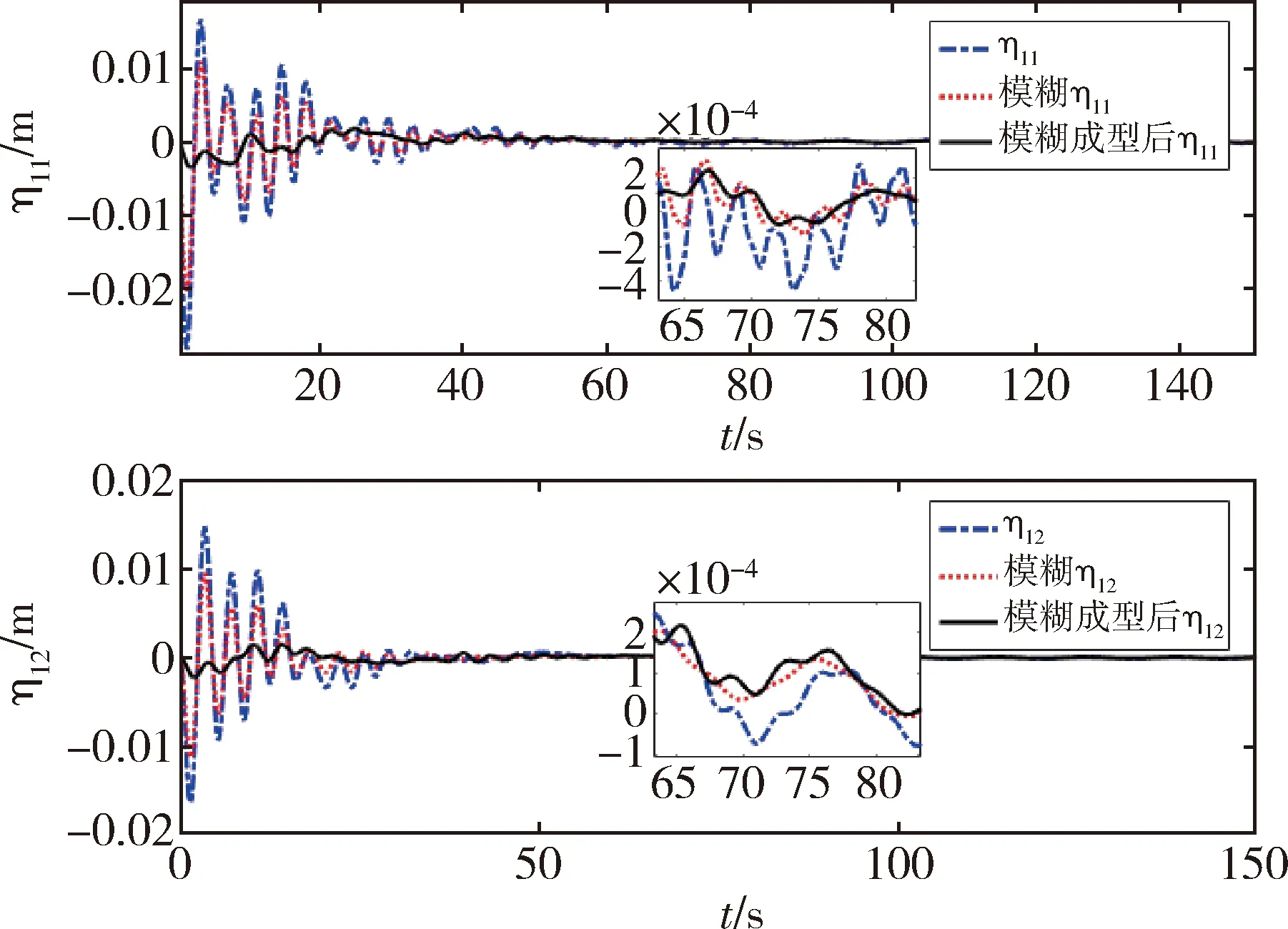
图6 一阶液体晃动响应Fig.6 First-order liquid sloshing responses
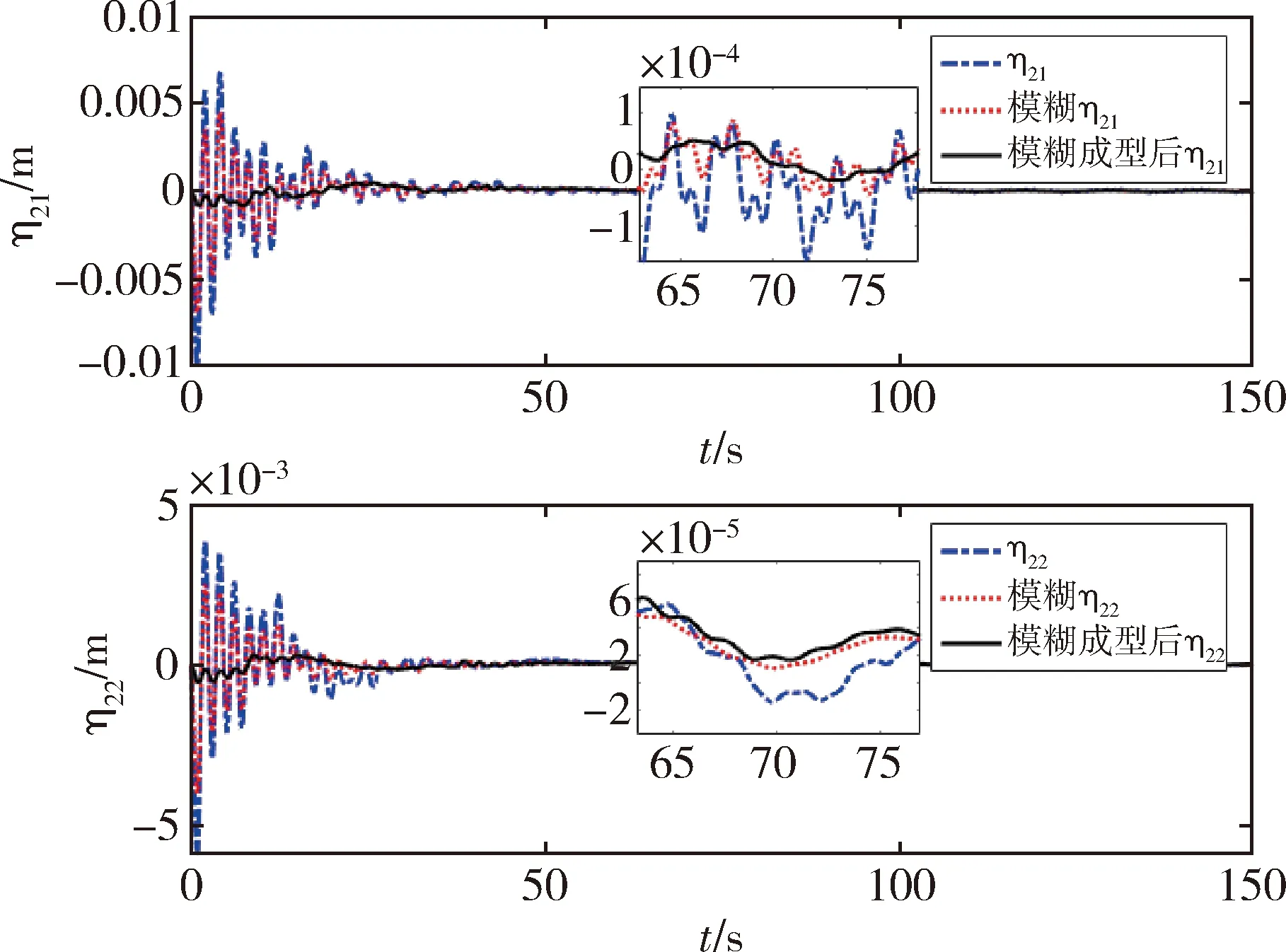
图7 二阶液体晃动响应Fig.7 Second-order liquid sloshing responses

图8 挠性附件前三阶模态坐标响应Fig.8 The first three-order modal coordinates of the flexible vibrations responses
4 结 论
本文针对挠性充液航天器在进行大角度姿态机动时的稳定性控制问题,首先建立了刚-挠-液三耦合的航天器动力学模型,其次考虑在大角度姿态机动时系统各状态变量不可测得、会受到未知的干扰力矩以及液体晃动和挠性附件振动的抑制问题,设计了结合模糊控制技术以及多模态输入成型技术的自适应输出反馈复合控制器,在保证系统稳定的前提下较为明显地抑制了系统姿态机动时引起的液体晃动及挠性振动的位移响应.仿真结果验证了本文的有效性.本复合控制器的优点在于:在自适应输出反馈控制律的基础上针对固定参数kp和kd进行了动态模糊优化,使航天器的姿态机动变化得更加平滑稳定,提高了系统的鲁棒性.将指令四元数作为系统的前馈输入,设计了基于多模态输入成型技术的前馈控制器,有效地减小了航天器在姿态机动时产生的液体晃动以及挠性附件的振动位移响应.

