具有方向约束的多智能体系统的反一致性研究
孔祥磊, 汪芳琴, 钟选明, 鲁中轩
中国空间技术研究院, 北京 100094
0 引 言
近几年,随着集群控制领域的发展,一致性[1-5]问题成为不同领域学者关注的重点,不同类型的一致性协议在不同的工程技术领域得到广泛应用.在卫星协同控制领域,通过设计非线性一致性协议,BONDHUS等[6]实现了无角速度测量信息的主-从编队姿态同步.在机器人控制领域,基于群体机器人队形一致性控制,徐志强等[7]设计了能够克服系统中噪声影响的领导者-跟随者的多机器人编队模型.在智能电网控制中,基于带时滞的一致性理论,CHEN等[8]提出了一种能源优化调度算法,解决了分布式电力系统出现的时滞问题等等.此外,一致性理论的典型应用还包括了包围控制[9]、可控性[10-13]、可镇定性[14-15]、编队控制[16-17]等等.
然而,在很多实际场景中,系统某些状态量趋于一致或相同并不能满足期望.如在航天控制中,由于太空垃圾越来越多,卫星和巨型星座运营者需要考虑如何实现卫星在运行过程中躲避这些卫星碎片.特别是在近地轨道,由于挤满了卫星和巨型星座,更加需要设计合理的防撞机制和轨道拥堵治理策略.在智能交通中,对同车道行驶的机动车,需要设计后车与前车保持足够的安全距离以防止车尾冲撞.在环保领域,部署的多台无人飞行器需要在指定区域内分散开以实现对环境的持续监控等.针对上述类似场景,多智能体系统的反一致性[18-19]理论结果存在巨大应用价值.
多智能体系统的反一致性问题是一个具有巨大潜在价值的研究课题.在文献[18]中,作者给出了一类反一致性协议设计方法,实现了所有智能体最终静止且彼此距离不低于指定值.进一步,作者讨论了有界范围内多智能体系统的反一致性问题,并给出了相应协议,保证系统在有界范围内达到反一致状态.在文献[19]中,作者讨论了一类非完整约束动力学系统的反一致性问题,实现了所有智能体避碰并达到指定队形.在文献[20]中,作者通过设计包含反一致性的控制律,解决了具有领航者的多智能体系统包围控制问题,最终实现了跟随者进入领航者构成的包围区域且演化过程避碰.值得说明的是,实际应用中,个体在空间中的运动往往是受方向约束的.如发射出去的导弹只能向前飞,卫星在轨运行时,很难绝对静止和后退.上述研究[18-20]中,均没有考虑智能体受方向约束时系统的反一致性问题.
本文研究了具有方向约束的多智能体系统的反一致性问题.首先,假设所有智能体在一维空间服从单向运动.通过设计反一致性协议,实现了所有智能体最终达到指定状态,满足反一致性条件.随后,将系统动力学模型推广到高阶,讨论了高阶多智能体系统的反一致性问题,并给出了一种控制律设计方法,实现了所有智能体最终实现指定的反一致状态.进一步,将系统从一维空间推广到N维空间.假设多智能体系统中智能体在N维空间运动,并在第k个坐标轴方向上沿正向运动,在其他方向上不受约束.通过设计智能体的控制输入,实现了系统中所有智能体最终达到反一致状态.最后仿真校验了主要理论成果.
与现有的研究成果相比,主要创新点在于:1)考虑了具有方向约束的多智能体系统的反一致性问题.首先讨论了智能体在一维空间中服从单向运动的反一致协议设计问题.其次,将系统从一维空间推广到N维空间,讨论了系统中智能体在N维空间沿第k个坐标轴的正向运动,在其他方向上不受约束时,系统的反一致性问题;2)系统中智能体仅仅通过观测其邻近智能体位置状态,自主分布式的决策和协调控制输入,最终实现整个系统在整体层面达到反一致状态;3)对提出的理论成果进一步扩展,可以解决更高阶、更复杂的系统模型.
1 准 备
1.1 矩阵理论
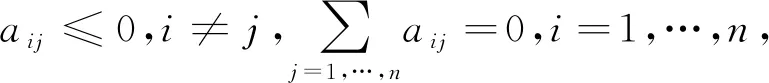
1)如果矩阵A为对称梅兹内矩阵,则矩阵A的所有特征值都是非负的实数,并且0是其平凡特征值.
2)如果矩阵A为对称梅兹内矩阵,则其特征值0是一重的,当且仅当对称梅兹内矩阵对应的无向通信拓扑图G是连通的.
2 多智能体系统的反一致性
2.1 系统模型
考虑多智能体系统具有n个智能体,标记为x1,…,xn,其中,xi∈RN,i=1,…,n,为了简化理论的证明,假设N=1,智能体xi的动力学模型为
(1)
其中,ui是智能体xi的控制输入.
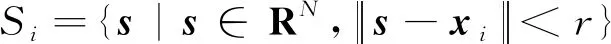
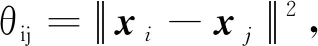
(2)
为θij的函数.其中,0
2.2 协议设计
不失一般性,假设多智能体系统(1)沿正方向做单向运动.智能体xi的控制输入设计如下:
(3)
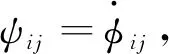
(4)
注1 根据协议(4),任意时刻t,当智能体的邻居智能体对其作用力小于0时,智能体状态保持不变,这保证了系统(1)中所有智能体在动力学演化过程中做单向运动.
2.3 主要定理
假设1在初始时刻,所有智能体x1,…,xn静止,所有智能体初始位置保证避碰,且至少存在一组xi,xj,i,j=1,…,n,满足dij≤r.
定理1在假设1的条件下,多智能体系统(1)使用控制律(4),可以实现所有智能体在动力学演化过程中避碰且服从单向运动,所有的智能体最终满足任意xi,xj,i,j=1,…,n,dij≥r.
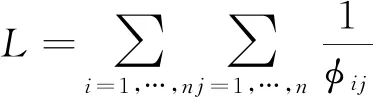
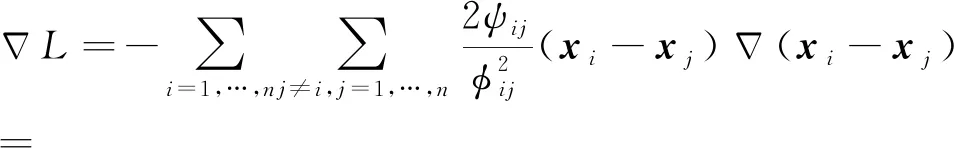
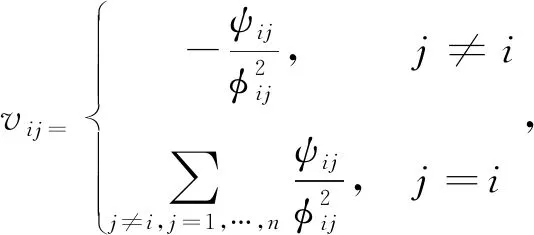
其中,α=[αi]n×1,且有αi=[Vx]i,β=[βi]n×1,且有当[Vx]i>0时,βi=αi,当[Vx]i≤0时,βi=0.显然,
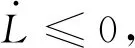
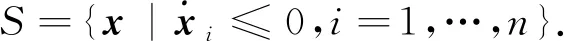
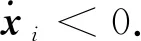
下面证明所有的智能体最终不仅静止,且满足任意xi,xj,i,j=1,…,n,dij≥r.假设当t→+∞,存在xi,xj,使得dij
注2 假设当xi→xj,有φij→0或φji→0,这会使得控制量趋向于无穷大,对于实际系统来说难以实现.然而在定理1中,由于李亚普诺夫函数单调递减,对任意的t∈[0,+∞),有所以提出的控制律均是有界控制,这避免了控制量趋向于无穷大.
假设N>1,即,智能体在高维空间运动,同时假设智能体在N维空间中沿第k个坐标轴的正向做单向运动,智能体xi的控制输入设计如下:
(5)
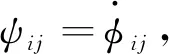
(6)
推论1在假设1的条件下,多智能体系统(1)使用控制律(6),可以实现所有智能体在动力学演化过程中避碰且在N维空间中沿第k个坐标轴的正向做单向运动,所有的智能体最终满足任意xi,xj,i,j=1,…,n,dij≥r.
注3 在实际应用中,令α表示N维空间中的方向向量,多智能体系统(1)满足所有智能体沿该方向做单向运动,只需调整控制律(6)满足智能体在α方向受到邻居施加的力小于等于0时,控制律为0.
注4 在实际应用中,r表示智能体传感器的测距范围.当多智能体系统中传感器测距范围不同时,此时多智能体系统作为异质系统,若要实现反一致状态,只需设计r满足03 高阶多智能体系统的反一致性
3.1 二阶系统模型
考虑多智能体系统中,智能体的动力学模型为二阶积分器形式
(7)
其中,vi表示智能体xi的速度.
3.2 协议设计
智能体的控制律设计如下:
(8)
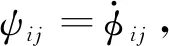
(9)
注5 根据协议(9),任意时刻t,当智能体检测到自身速度降低为0时,且智能体邻居对其作用力为反向,智能体状态保持不变,这保证了系统(7)中所有智能体在动力学演化过程中做单向运动.
3.3 主要定理
假设2在初始时刻,系统中的智能体x1,…,xn的速度v1,…,vn满足vi≥0,i=1,…,n.
定理2在假设1和假设2条件下,多智能体系统(7)使用控制律(9),可以实现所有智能体在动力学演化过程中避碰且服从单向运动,所有的智能体最终静止且满足任意xi,xj,i,j=1,…,n,dij≥r.
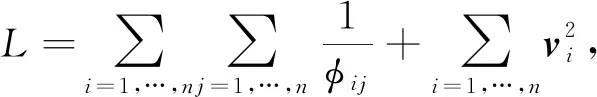
其中,x,V=[vij]n×n定义如上.结合控制律(9),有李亚普诺夫函数L的导数
其中,v=[v1,…,vn]T,α=[αi]n×1,β=[βi]n×1,且有当[Vx]i<0,vi≤0时,αi=βi=0,否则,αi=[Vx]i,βi=vi.李亚普诺夫函数L的导数等价于
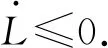

根据拉萨尔不变集原理,所有智能体x1,…,xn是在动力学演化过程中,最终状态稳定到不变集
由于协议(9)的设计保证了系统中所有智能体xi的速度vi≥0,所以有任意l=lj,j=1,…,h,vl=0,故S等价于S={x,v|vi=0,i=1,…,n},所以智能体x1,…,xn最终静止.
下面说明,所以智能体x1,…,xn最终静止当且仅当[Vx]i=0,i=1,…,n.假设存在智能体xi,满足[Vx]i≠0,即,Ni≠0.考虑多智能体系统中,xi所在的最大连通子图为G={xl1,…,xlh},即任意的xi∈G,存在xj∈G,满足dij0,根据控制律(9),下一刻,vl>0,矛盾,所以智能体x1,…,xn最终静止且满足[Vx]i=0,i=1,…,n,即,任意的智能体xi,xj,i,j=1,…,n,dij≥r.所以定理2得证.
假设N>1,即,智能体在高维空间运动,设计智能体在N维空间中沿第k个坐标轴的正向做单向运动,设计智能体xi的控制输入如下:
(10)
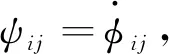
(11)
推论2在假设1和假设2条件下,多智能体系统(7)使用控制律(11),可以实现所有智能体在动力学演化过程中避碰且在N维空间中沿第k个坐标轴的正向做单向运动,所有的智能体最终静止且满足任意xi,xj,i,j=1,…,n,dij≥r.
注6 在定理1和定理2中,所有智能体状态最终静止.将上述理论进行推广,可以实现多智能体系统中所有智能体动力学演化过程避碰且服从单向运动,同时所有智能体最终状态达到指定队形,即,多智能体系统实现编队控制,只需在系统中增加若干个领航者,领航者接收外部控制指令.
4 数值实例
下面通过数值实例1~2校验上述定理和推论的主要理论结果.
4.1 数值实例1
下面通过数值实例校验定理1和推论1的理论结果.假设多智能体系统中存在13个智能体,其形式表示为xi=[xi1,xi2]T∈R2,所有智能体在平面沿xi2坐标轴正向运动,系统参数c=1,k1=1,智能体感知半径r=2,通过计算,得到k2=2.5,a0=-0.16666667,a1=1.33333333,a2=-0.16666667.初始时刻,随机选取智能体位置满足,所有智能体保证避碰,且至少存在一组智能体,其之间的距离小于感知半径r=2.图1表示所有智能体的状态轨迹,其中,圆点表示智能体初始时刻位置,三角表示智能体在t=50000时的位置,可以看出所有智能体在状态演化过程中,位置随时间渐近分散.图2表示智能体轨迹演化的俯视图,从中可以看出,所有智能体沿xi2坐标轴正向运动.图3为t=50000时刻所有智能体位置俯视图,其中圆环为以智能体为圆心,r=2为半径,可以看出,随着时间增大,任意一组智能体的距离渐近大于等于感知半径,其与定理1和推论1的理论结果一致.
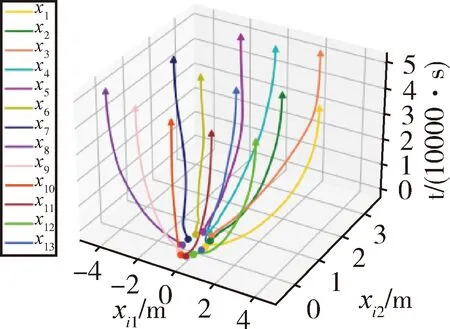
图1 位置演化轨迹Fig.1 Position evolution trajectory
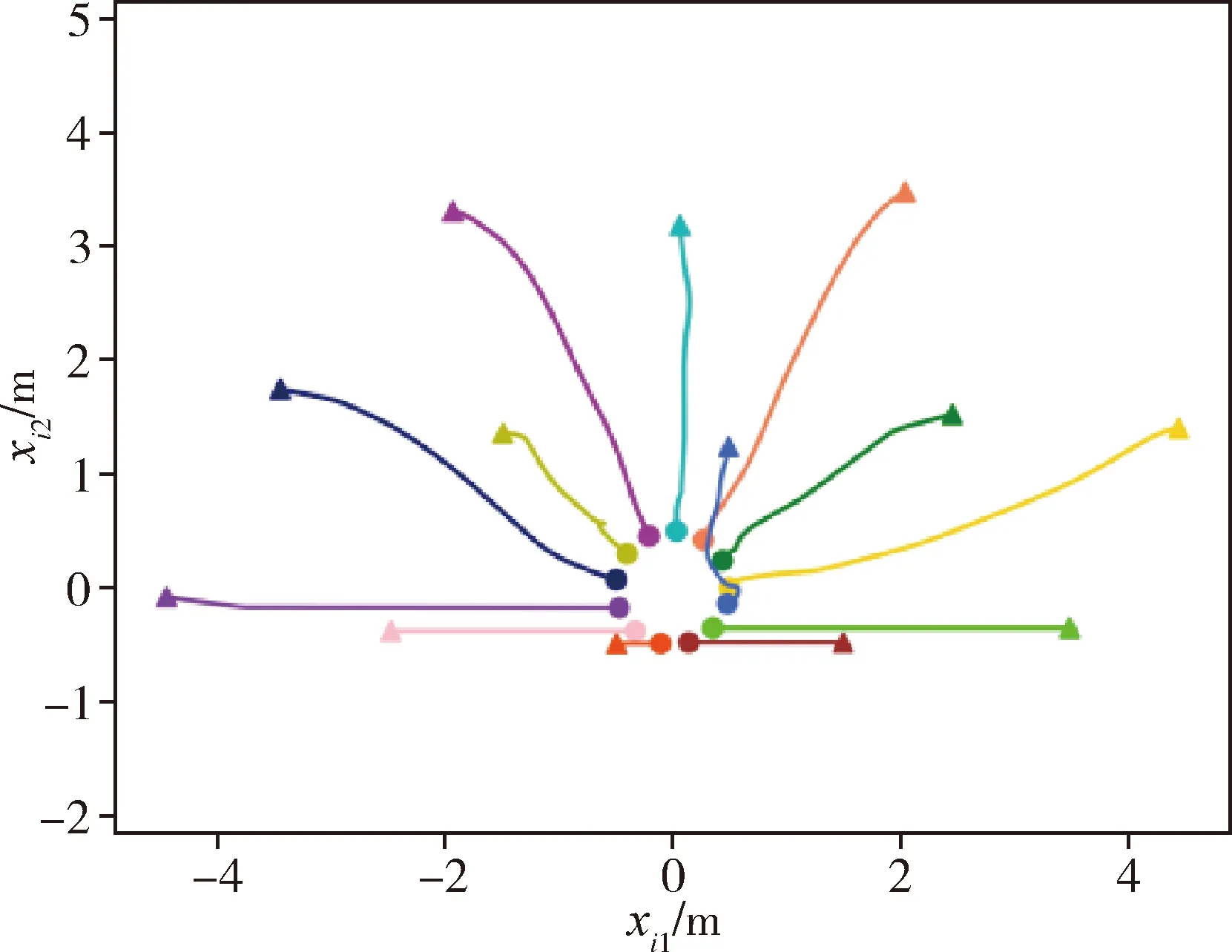
图2 位置演化俯视图Fig.2 Top view of position evolution
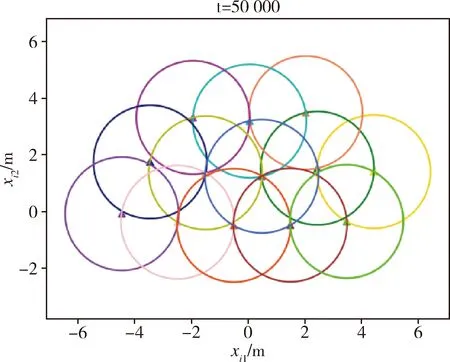
图3 t=50000时刻俯视图Fig.3 Top view of position at time t=50000
4.2 数值实例2
接下来校验定理2和推论2的理论结果.假设多智能体系统中存在13个智能体,其形式表示为xi=[xi1,xi2]T∈R2,所有智能体在平面沿xi2坐标轴正向运动,系统参数和感知半径如数值实例1.初始时刻,随机选取智能体位置和速度满足,所有智能体保证避碰,且至少存在一组智能体,其之间的距离小于感知半径r=2,所有智能体速度分量vi2不小于0.图4表示所有智能体的状态演化轨迹,其中,圆点表示智能体初始时刻位置,三角表示智能体在t=50000时的位置,可以看出所有智能体在状态演化过程中,位置随时间渐近分散.图5表示所有智能体速度演化过程,其中虚线表示满足的vi1=vi2=0的直线,可以看出,随着时间增加,所有智能体的速度趋于0.图6表示智能体轨迹演化的俯视
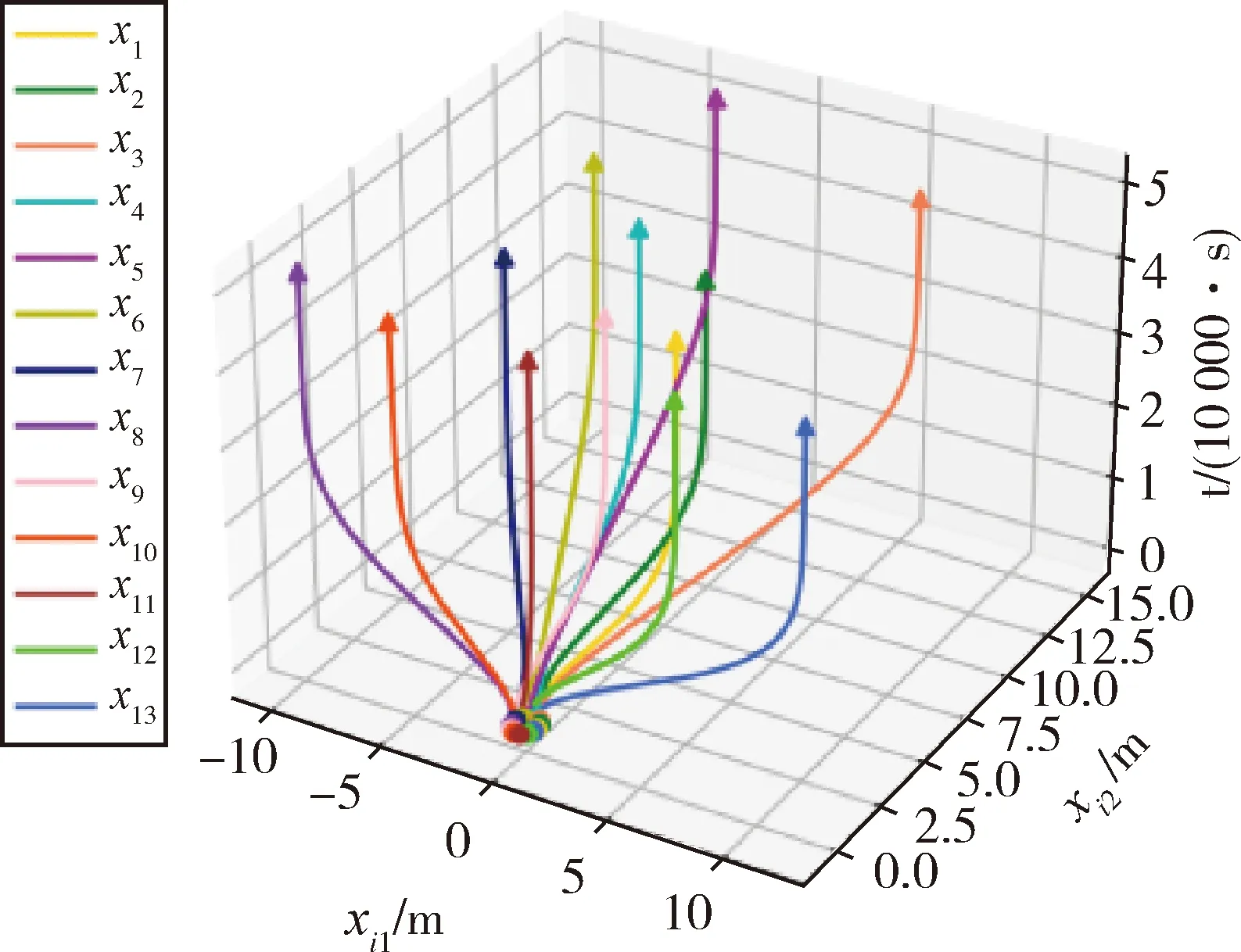
图4 位置演化轨迹Fig.4 Position evolution trajectory
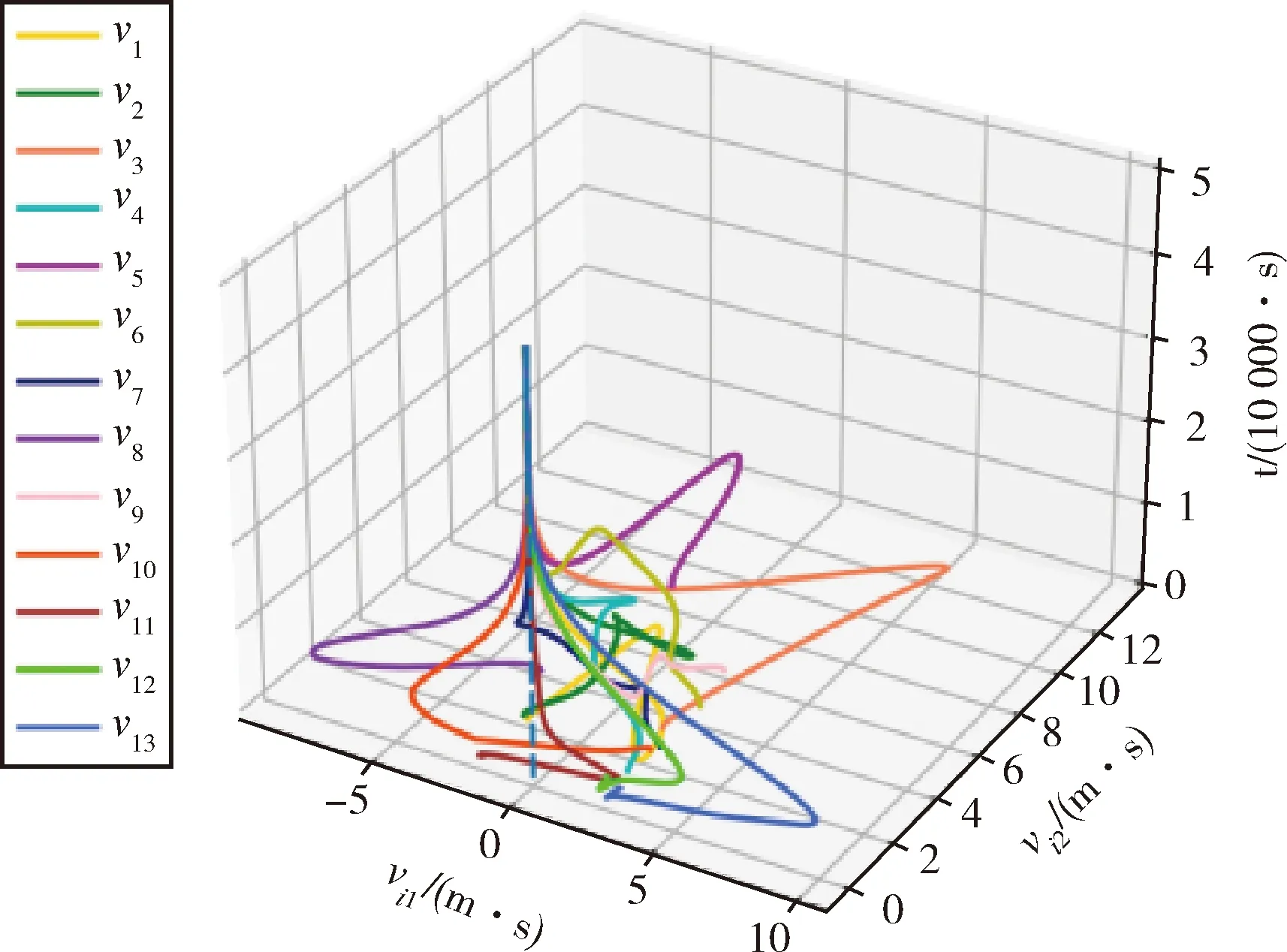
图5 速度演化轨迹Fig.5 Velocity evolution trajectory
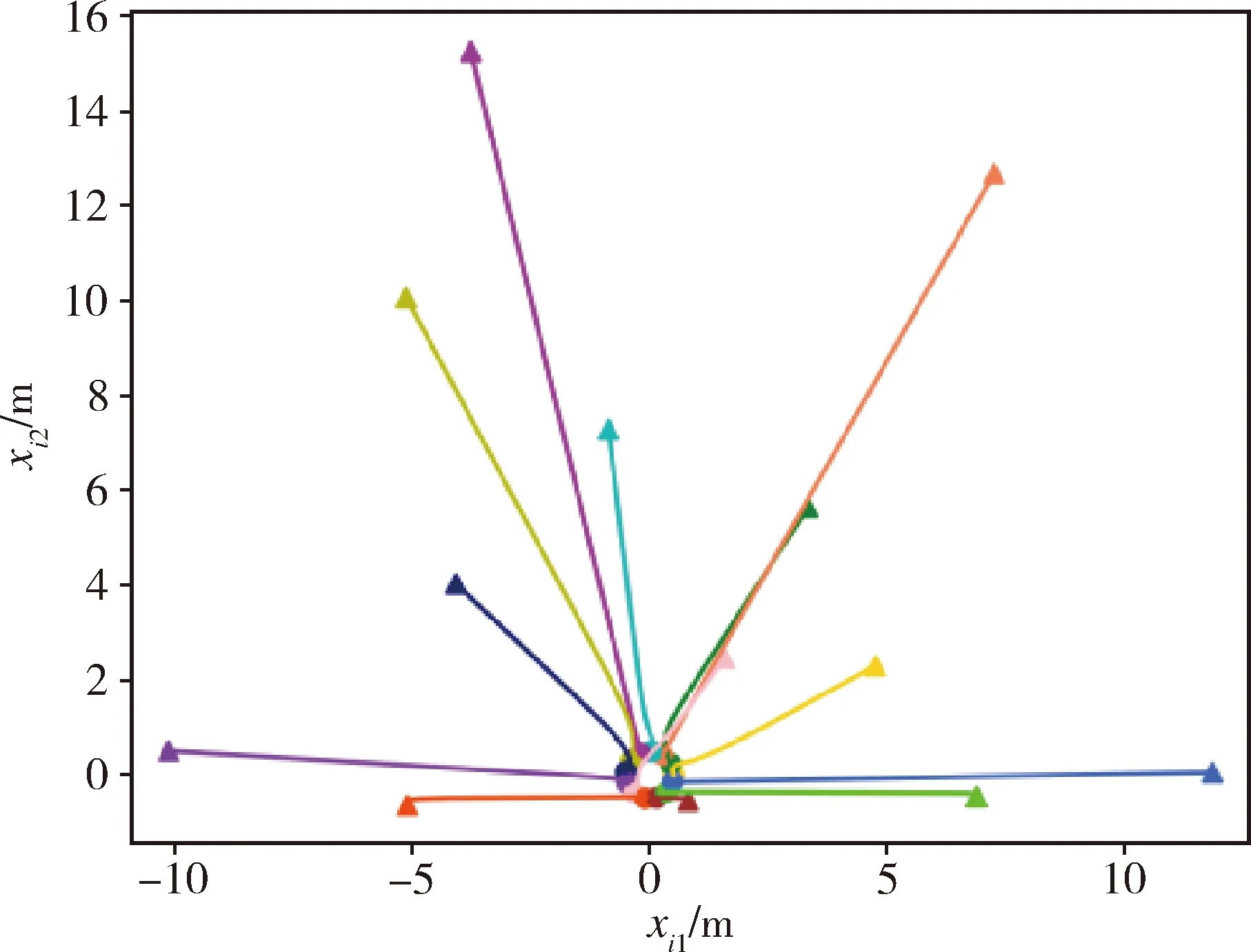
图6 位置演化俯视图Fig.6 Top view of position evolution
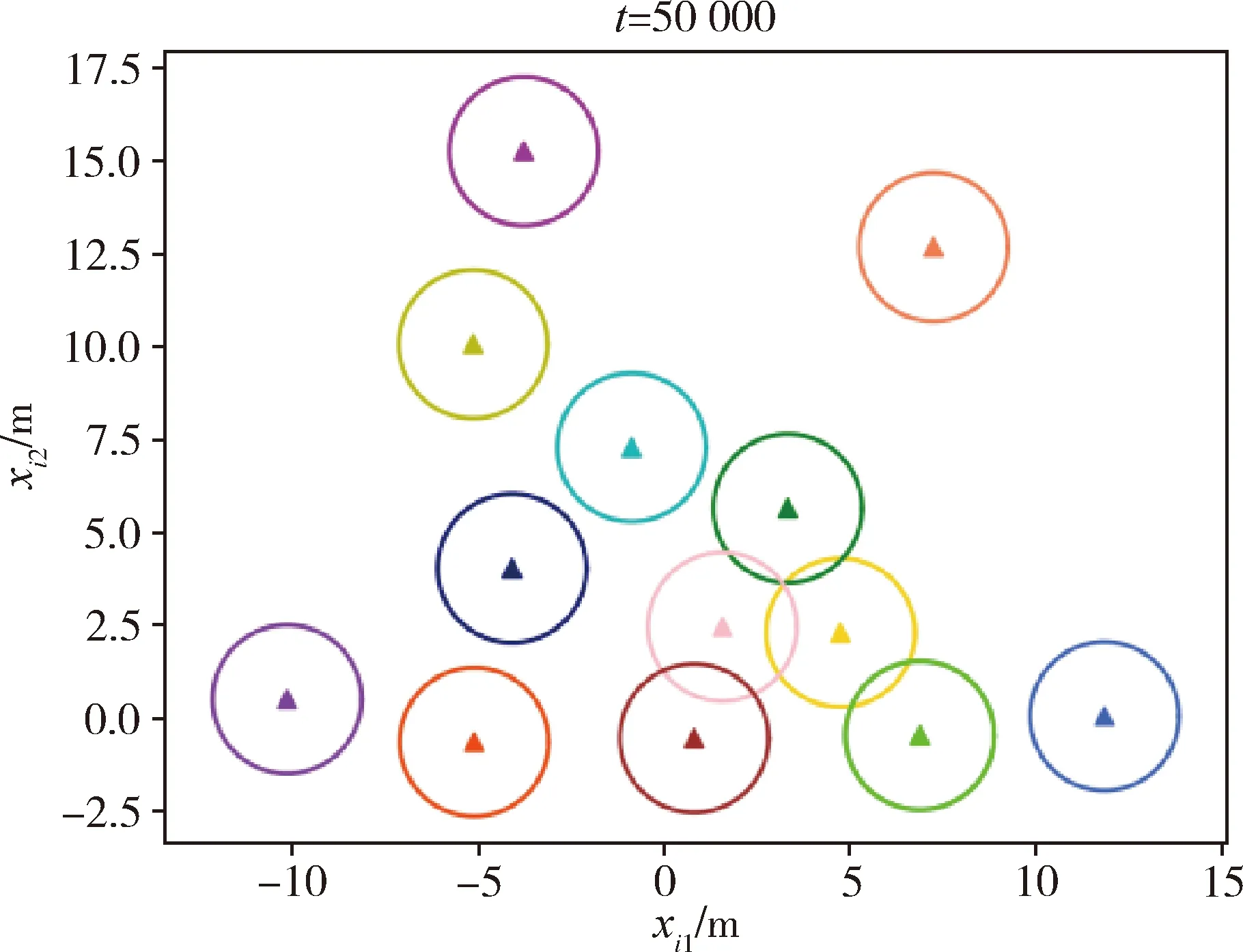
图7 t=50000时刻俯视图Fig.7 Top view of position at time t=50000
图,从中可以看出,所有智能体沿xi2坐标轴正向运动.图7为t=50000时刻所有智能体位置俯视图,其中圆环为以智能体为圆心,r=2为半径,可以看出,随着时间增大,任意一组智能体的距离渐近大于等于感知半径,其与定理2和推论2的理论结果一致.
5 结 论
研究了具有方向约束的多智能体系统的反一致性问题.对服从单向运动的一维多智能体系统,给出了一类反一致性协议设计方法,实现了所有智能体避碰并最终状态满足任意一组智能体,其之间的距离不小于感知半径.进一步,针对二阶多智能体系统,给出了一类包含速度的反一致协议设计方法,系统中智能体仅仅通过观测其邻近智能体位置状态和检测自身速度,最终实现整个系统在整体层面达到反一致状态.最后,将系统从一维空间推广到N维空间,给出了系统中所有智能体在N维空间第k个坐标轴方向上沿正向运动,在其他方向上不受约束时,系统实现反一致性状态的协议.给出的仿真实例说明了该方法的有效性.
猜你喜欢
生命的演化过程娃娃乐园·综合智能(2023年6期)2023-06-14 07:01:52 用坐标轴平移妙解斜率和(或积)为定值问题数理化解题研究(2021年34期)2021-12-26 08:32:02 模因论视角下韩语“먹다”表“喝”动作演化过程研究韩国语教学与研究(2021年2期)2021-11-24 01:11:40 时间非齐次二态量子游荡的演化过程分析数学物理学报(2021年4期)2021-08-30 08:28:08 重庆万盛石林的形成时代及发育演化过程四川地质学报(2020年2期)2020-05-31 06:53:34 Update on Fengyun Meteorological Satellite Program and Development*空间科学学报(2020年5期)2020-04-16 13:55:46 从零维到十维的空间之旅大众科学(2016年11期)2016-11-30 15:28:35 巧用仿射变换妙解高考解析几何题中学生数理化·高二版(2016年7期)2016-05-14 13:19:34 十维空间的来访者科学启蒙(2015年9期)2015-09-25 04:01:05 坐标轴平移中配方的技巧新一代(2011年2期)2011-06-17 09:29:50
3 高阶多智能体系统的反一致性
3.1 二阶系统模型
考虑多智能体系统中,智能体的动力学模型为二阶积分器形式
(7)
其中,vi表示智能体xi的速度.
3.2 协议设计
智能体的控制律设计如下:
(8)
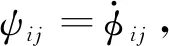
(9)
注5 根据协议(9),任意时刻t,当智能体检测到自身速度降低为0时,且智能体邻居对其作用力为反向,智能体状态保持不变,这保证了系统(7)中所有智能体在动力学演化过程中做单向运动.
3.3 主要定理
假设2在初始时刻,系统中的智能体x1,…,xn的速度v1,…,vn满足vi≥0,i=1,…,n.
定理2在假设1和假设2条件下,多智能体系统(7)使用控制律(9),可以实现所有智能体在动力学演化过程中避碰且服从单向运动,所有的智能体最终静止且满足任意xi,xj,i,j=1,…,n,dij≥r.
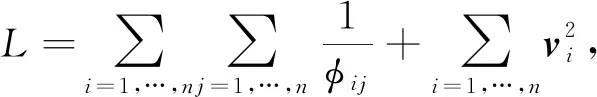
其中,x,V=[vij]n×n定义如上.结合控制律(9),有李亚普诺夫函数L的导数
其中,v=[v1,…,vn]T,α=[αi]n×1,β=[βi]n×1,且有当[Vx]i<0,vi≤0时,αi=βi=0,否则,αi=[Vx]i,βi=vi.李亚普诺夫函数L的导数等价于


根据拉萨尔不变集原理,所有智能体x1,…,xn是在动力学演化过程中,最终状态稳定到不变集
由于协议(9)的设计保证了系统中所有智能体xi的速度vi≥0,所以有任意l=lj,j=1,…,h,vl=0,故S等价于S={x,v|vi=0,i=1,…,n},所以智能体x1,…,xn最终静止.
下面说明,所以智能体x1,…,xn最终静止当且仅当[Vx]i=0,i=1,…,n.假设存在智能体xi,满足[Vx]i≠0,即,Ni≠0.考虑多智能体系统中,xi所在的最大连通子图为G={xl1,…,xlh},即任意的xi∈G,存在xj∈G,满足dij
假设N>1,即,智能体在高维空间运动,设计智能体在N维空间中沿第k个坐标轴的正向做单向运动,设计智能体xi的控制输入如下:
(10)
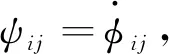
(11)
推论2在假设1和假设2条件下,多智能体系统(7)使用控制律(11),可以实现所有智能体在动力学演化过程中避碰且在N维空间中沿第k个坐标轴的正向做单向运动,所有的智能体最终静止且满足任意xi,xj,i,j=1,…,n,dij≥r.
注6 在定理1和定理2中,所有智能体状态最终静止.将上述理论进行推广,可以实现多智能体系统中所有智能体动力学演化过程避碰且服从单向运动,同时所有智能体最终状态达到指定队形,即,多智能体系统实现编队控制,只需在系统中增加若干个领航者,领航者接收外部控制指令.
4 数值实例
下面通过数值实例1~2校验上述定理和推论的主要理论结果.
4.1 数值实例1
下面通过数值实例校验定理1和推论1的理论结果.假设多智能体系统中存在13个智能体,其形式表示为xi=[xi1,xi2]T∈R2,所有智能体在平面沿xi2坐标轴正向运动,系统参数c=1,k1=1,智能体感知半径r=2,通过计算,得到k2=2.5,a0=-0.16666667,a1=1.33333333,a2=-0.16666667.初始时刻,随机选取智能体位置满足,所有智能体保证避碰,且至少存在一组智能体,其之间的距离小于感知半径r=2.图1表示所有智能体的状态轨迹,其中,圆点表示智能体初始时刻位置,三角表示智能体在t=50000时的位置,可以看出所有智能体在状态演化过程中,位置随时间渐近分散.图2表示智能体轨迹演化的俯视图,从中可以看出,所有智能体沿xi2坐标轴正向运动.图3为t=50000时刻所有智能体位置俯视图,其中圆环为以智能体为圆心,r=2为半径,可以看出,随着时间增大,任意一组智能体的距离渐近大于等于感知半径,其与定理1和推论1的理论结果一致.

图1 位置演化轨迹Fig.1 Position evolution trajectory

图2 位置演化俯视图Fig.2 Top view of position evolution

图3 t=50000时刻俯视图Fig.3 Top view of position at time t=50000
4.2 数值实例2
接下来校验定理2和推论2的理论结果.假设多智能体系统中存在13个智能体,其形式表示为xi=[xi1,xi2]T∈R2,所有智能体在平面沿xi2坐标轴正向运动,系统参数和感知半径如数值实例1.初始时刻,随机选取智能体位置和速度满足,所有智能体保证避碰,且至少存在一组智能体,其之间的距离小于感知半径r=2,所有智能体速度分量vi2不小于0.图4表示所有智能体的状态演化轨迹,其中,圆点表示智能体初始时刻位置,三角表示智能体在t=50000时的位置,可以看出所有智能体在状态演化过程中,位置随时间渐近分散.图5表示所有智能体速度演化过程,其中虚线表示满足的vi1=vi2=0的直线,可以看出,随着时间增加,所有智能体的速度趋于0.图6表示智能体轨迹演化的俯视

图4 位置演化轨迹Fig.4 Position evolution trajectory

图5 速度演化轨迹Fig.5 Velocity evolution trajectory

图6 位置演化俯视图Fig.6 Top view of position evolution

图7 t=50000时刻俯视图Fig.7 Top view of position at time t=50000
图,从中可以看出,所有智能体沿xi2坐标轴正向运动.图7为t=50000时刻所有智能体位置俯视图,其中圆环为以智能体为圆心,r=2为半径,可以看出,随着时间增大,任意一组智能体的距离渐近大于等于感知半径,其与定理2和推论2的理论结果一致.
5 结 论
研究了具有方向约束的多智能体系统的反一致性问题.对服从单向运动的一维多智能体系统,给出了一类反一致性协议设计方法,实现了所有智能体避碰并最终状态满足任意一组智能体,其之间的距离不小于感知半径.进一步,针对二阶多智能体系统,给出了一类包含速度的反一致协议设计方法,系统中智能体仅仅通过观测其邻近智能体位置状态和检测自身速度,最终实现整个系统在整体层面达到反一致状态.最后,将系统从一维空间推广到N维空间,给出了系统中所有智能体在N维空间第k个坐标轴方向上沿正向运动,在其他方向上不受约束时,系统实现反一致性状态的协议.给出的仿真实例说明了该方法的有效性.

