螺旋探索与自适应混合变异的麻雀搜索算法
陈 功,曾国辉,黄 勃,刘 瑾
(上海工程技术大学 电子电气工程学院,上海 201620) E-mail:cg540865935@163.com
1 引 言
为解决传统优化算法在求解复杂优化问题时存在计算量大,求解效率低的问题,学者们受自然启发,提出了许多智能优化算法,如:粒子群算法、差分进化算法、灰狼优化算法、正余弦算法、鲸鱼优化算法、麻雀搜索算法等.其中麻雀搜索算法(Sparrow Search Algorithm,SSA)是薛建凯等[1]于2020年提出了一种新型群智能算法,相较于传统智能优化算法,麻雀搜索算法具有结构简单、调节参数少,局部搜索能力强的优点,在图像[2]、电力[3]、航空[4]、医学[5]等领域有了广泛应用.麻雀搜索算法在求解单峰、多峰函数等基准函数上的表现优于粒子群算法、差分进化算法等传统算法,但是在处理局部最优解不在原点附近的函数时,容易陷入局部最优.
为了改善麻雀搜索算法抗局部最优能力弱的缺陷,许多学者提出了改进方法:Chen等人[6]采用Tent混沌初始化麻雀种群,并引入莱维飞行和随机游走策略有效改善了算法的收敛速度和探索能力;Zhang等人[7]将正余弦算法引入麻雀搜索算法中,并提出一种新的劳动协作结构,提高了算法跳出局部最优的能力;Zhang等人[8]利用Logistic映射初始化种群,并采用柯西变异算子对最优麻雀位置进行扰动,提高了算法的全局搜索能力;Ouyang等人[9]利用k-means聚类方法对麻雀个体位置进行聚类和区分,摆脱了随机性对初始种群的影响;毛清华等人[10]利用柯西变异和反向学习在最优麻雀位置进行扰动变异,增强了算法跳出局部空间的能力;段玉先等人[11]利用Sobol序列初始化麻雀种群,并引入纵横交叉算子,克服了算法易陷入局部最优的缺点;柳长安等人[12]将反向学习和自适应t分布变异策略融入麻雀搜索算法中,增强了算法后期局部搜索能力.
虽然上述改进方法在一定程度上提升了算法的搜索性能,但SSA算法仍有很大的改进空间.为了使算法同时拥有较好的收敛性能和收敛精度,进一步加强SSA算法的性能,本文在已有研究基础上,提出一种螺旋探索与自适应混合变异的麻雀搜索算法(Spiral exploration Hybrid mutation Sparrow Search Algorithm SHSSA),从3个方面对SSA算法进行改进:1)利用ICMIC混沌初始化种群,增加种群多样性,为全局寻优奠定基础;2)提出一种螺旋探索策略,改善算法的全局搜索性能;3)提出一种混合变异策略,提高算法的收敛速度与跳出局部最优的能力.通过对12个基准测试函数的仿真测试,证明了改进策略的有效性;最后将该算法应用于图像分割中,仿真结果表明SHSSA算法的分割精度更高、分割速度更快.
2 基本麻雀搜索算法
麻雀搜索算法是模拟麻雀觅食行为的一种群智能优化算法,麻雀种群由发现者-跟随者组成,并带有侦察预警机制.发现者的适应度更好,能够在较大范围内主动寻找食物;适应度较差的跟随者跟随发现者进行觅食.当遇到捕食者威胁时,侦察者会发出警报,使整个种群向安全的地方转移.
麻雀个体在搜索空间中的位置可由矩阵X表示:
Xi=[xi1,…,xid,…,xiD]
(1)
式中,xid为第i只麻雀在d维空间的位置.麻雀个体通过在搜索空间中不断更新位置来改善自身适应度.其中,发现者占整个种群的10%~20%,位置更新方式如下:
(2)
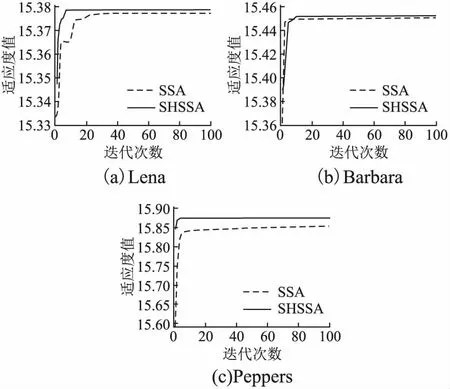
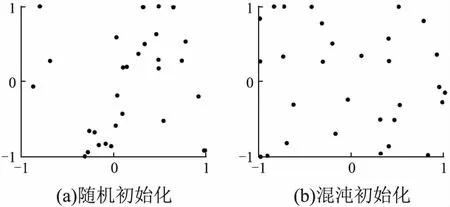
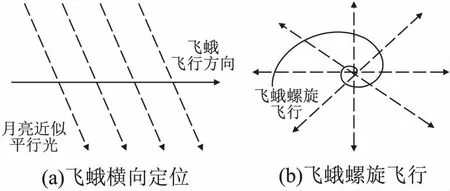
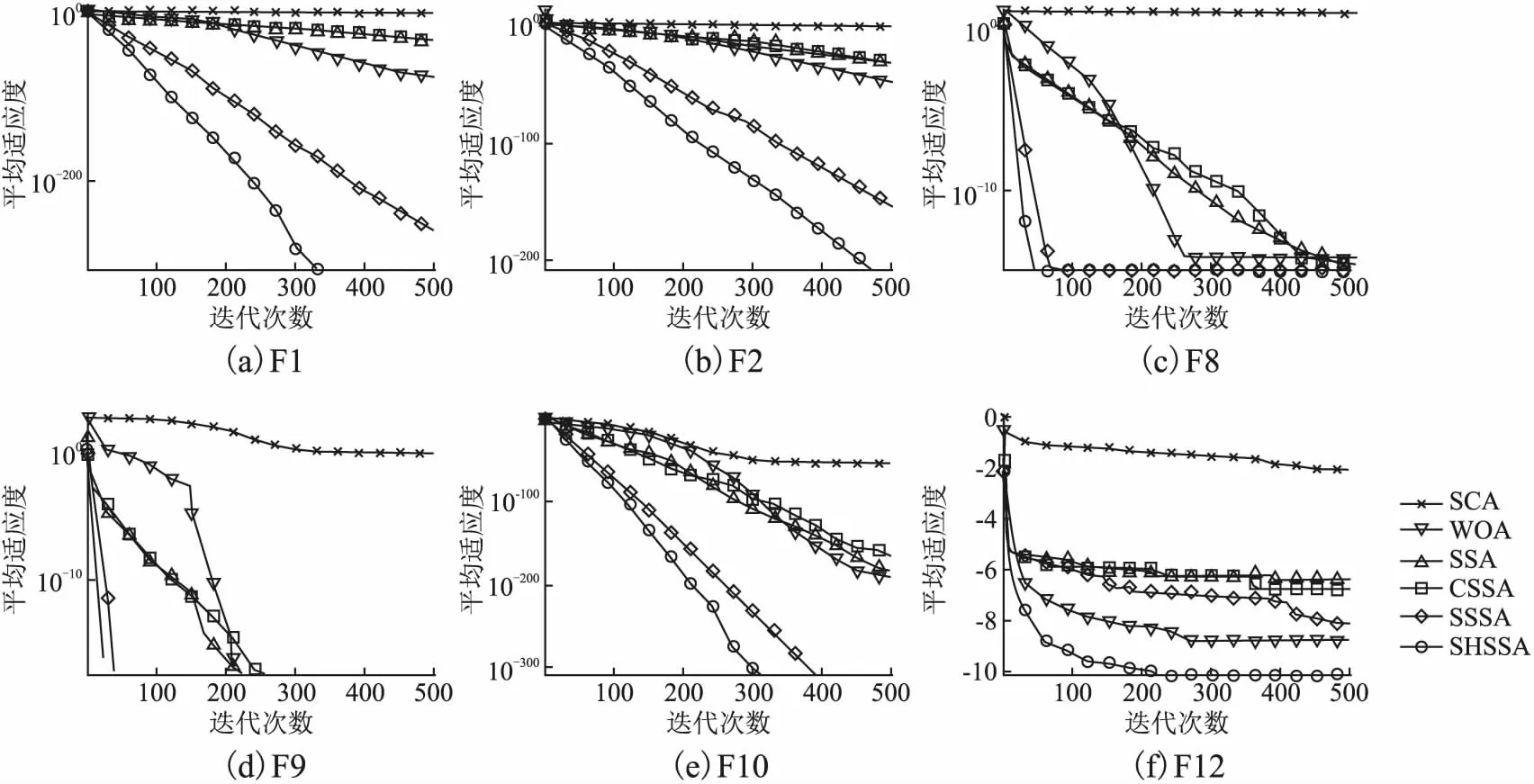
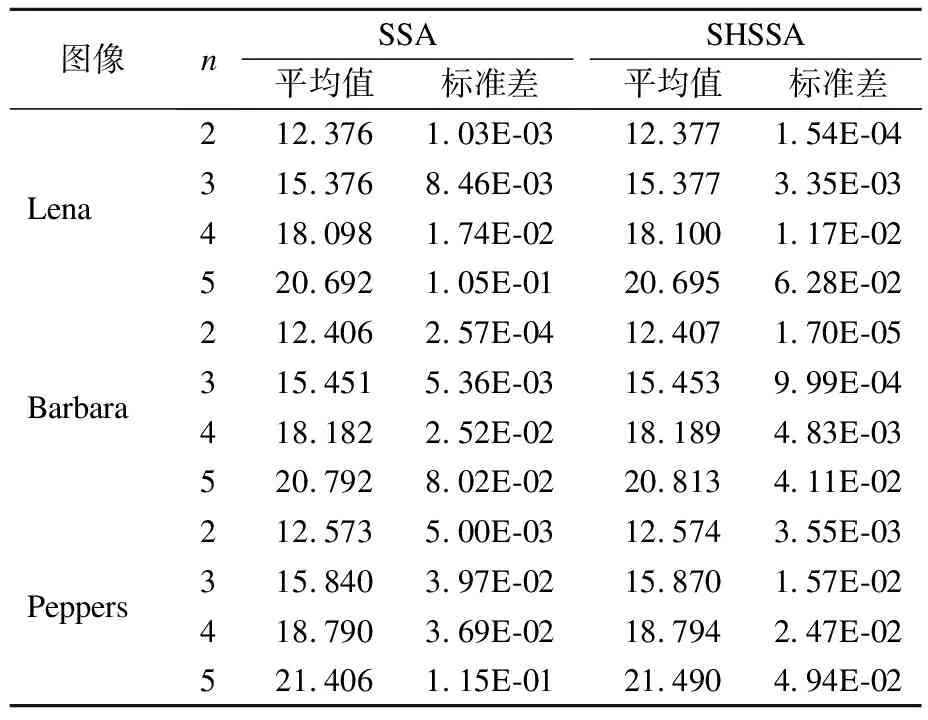
式中:T为最大迭代次数,α为0-1之间的随机数,Q为服从正态分布的随机数,L为元素均为1的1×d矩阵.R2∈[0,1]为警戒值,ST∈[0.5,1]为安全值.当R2 整个种群中,除了发现者,剩余全部为跟随者,跟随者位置更新方式如下: (3) 侦察预警行为: 麻雀在觅食时,会选取少量麻雀负责警戒,来躲避捕食者攻击.侦察者占种群的10%~20%,其位置更新公式如下: (4) 式中:β是服从均值为0,方差为1的正态分布随机数;K表示麻雀移动方向,为-1~1之间的随机数;e为极小常数,避免除数为0;当fi(第i只麻雀适应度)≠fg(最优麻雀适应度)时,表示该麻雀处于种群边缘,易受到捕食者攻击,此时会向最优麻雀靠近.当fi=fg时,表示处于种群中间的麻雀意识到了危险,此时需要靠近其它麻雀来减少被捕食的风险. 在群智能优化算法中,初始种群的分布状态,对于算法的收敛速度和寻优精度至关重要.在处理未知分布问题时,初始种群应尽可能均匀分布在搜索空间中,保持较高的多样性.在SSA中,采用随机变量生成初始种群,这种方法遍历性较低,个体分布不均匀,一定程度上影响了算法的寻优性能. 混沌变量具有遍历性和规律性,常被应用于优化问题中.Logistic映射和Tent映射是最常用的混沌模型,但是两者在迭代区域内的折叠次数有限,且存在有理数不动点.文献[13]提出的ICMIC映射是一种映射折叠次数无线的混沌模型,相较于Logistic映射和Tent映射,该映射具有遍历均匀和收敛较快等优点.因此本文采用ICMIC映射初始化SSA种群,ICMIC映射的数学表达式如下: (5) 将ICMIC混沌映射到搜索空间中,得到种群初始位置: (6) 其中xlb、xub分别为每个个体在各维度的上下界,zi为式(5)产生的混沌序列. 图1 初始化种群分布图Fig.1 Initialized population distribution graph 假设种群规模为30,两种方法在二维搜索空间中产生的初始化种群分布图如图1所示,从图中可以看出,相比随机序列,通过ICMIC混沌序列产生的初始种群分布更均匀,遍历性更好. 在SSA中,发现者作为优势群体,在解空间区域内进行大范围搜索觅食;跟随者受发现者引领,在发现者周围进行详细搜索.可见,发现者的全局勘探能力更强,跟随者则更擅长局部开发.实际上,由公式(2)可知,当R2 图2 飞蛾飞行示意图Fig.2 Flight diagram of moth 飞蛾是一种类似于蝴蝶的昆虫,在夜间飞行时采用横向定位机制来导航.如图2所示,在这种机制中,飞蛾通过保持相对于月亮的固定角度飞行.由于月亮离飞蛾很远,飞蛾利用这种近似的平行光可以保持直线飞行.但实际中存在很多人造光源,这种光源距离飞蛾非常近,当飞蛾与人造光源保持固定角度飞行时,就会导致横向定位机制失效,产生围绕光源螺旋式的飞行路径.受飞蛾螺旋飞行的启发,本文在发现者位置更新方式中加入一种螺旋探索因子,使得发现者拥有多种搜索路径来更好的调整自身位置,从而提高算法的全局搜索性能.具备螺旋探索的发现者位置更新公式如下: (7) 式中:z为螺旋探索因子,b为螺旋形状常数,p表示路径系数,为[-1,1]中的随机数. 融入螺旋探索后,发现者将以螺旋形式在搜索空间中搜索,扩展了发现者探索未知区域的能力,使算法跳出局部最优的可能性增加,有效提高算法的全局搜索性能. 基本SSA算法最优个体的更新依赖于每次迭代种群的更新,即每次迭代后,由当前适应度最好的个体替代最优个体,算法没有主动对最优个体进行扰动.若最优个体陷入局部极值空间,则会导致算法难以跳出局部最优,出现早熟收敛现象.为了加快算法收敛速度、改善算法跳出局部最优的能力,本文提出一种自适应混合变异策略,在每次迭代后对最优麻雀进行扰动. 3.3.1 精英差分变异 差分进化是利用当前种群的距离和方向信息指引搜索的一种进化算法[14].该算法在变异阶段,通过随机选择的两个个体的差向量加权后与第3个个体相加来产生新个体,即: (8) 式中,F∈[0,2]为缩放因子.文献[15]指出,缩放因子F太大时,算法近似随机搜索,寻优精度降低;当F太小时,种群多样性下降很快,算法容易陷入局部最优. 通过上述分析可知,差分进化受参数F的影响较大,且随机选择差分个体具有盲目性.考虑到精英个体包含更多有益信息,为了加强精英个体间的信息交流,本文提出一种精英差分变异策略,公式如下: (9) 式中,r1、r2为(0,1)的随机数.xbest为最优解,x2为次优解,x3为第3优解. 式(9)中舍弃了缩放因子,不需要考虑参数选择对算法性能的影响;精英解的引入,使得算法的进化方向更明确,不再具有盲目性.在算法迭代后,通过式(9)产生新解,能够提升算法在当前最优解附近发现全局最优解的可能性. 3.3.2 随机反向学习 反向学习是Tizhoosh[16]提出的一种优化策略,该策略通过计算当前解在搜索空间中的反向解来扩大搜索范围.一般反向学习的数学表达式如下: (10) 文献[17]表明一般反向学习在算法迭代前期作用显著,而在算法迭代后期作用不明显.因为在迭代后期,大部分个体集中在小范围区域,反向解所在区域也集中于此,所以通过一般反向学习的方式很难跳出当前极值区域.针对该问题,本文提出一种新的随机反向学习策略,通过在一般反向学习中引入随机因子,进一步扩展反向解位置,增强算法跳出局部极值的能力.随机反向学习的公式如下: (11) 式中,k1和k2为随机因子,均为0~1之间的随机数. 3.3.3 自适应混合变异 SSA算法求得全局最优解的关键是算法能否有效跳出局部最优.若只是加入单一的变异策略,则在加快收敛速度的同时也会导致算法陷入局部最优.因此,本文将精英差分变异和随机反向学习融入到SSA中,利用判定系数r对最优麻雀位置进行混合变异扰动.如公式(12)所示,当r<0.5时,采用精英差分策略进行小范围扰动;当r≥0.5时,采用随机反向策略进行大范围扰动.两种策略相辅相成,促使算法跳出局部极值空间,在求解不同优化问题时的适应性更强. (12) 其中r为0~1的随机数. 由于变异后的麻雀位置不一定由于原始位置,因此,采用贪婪策略,选择是否将原始解用变异解替代,即只有当变异解的适应度值优于原始解时才进行替换,公式如下: (13) 其中x′为贪婪选择后最优麻雀的位置. 螺旋探索与自适应混合变异的麻雀搜索算法伪代码如算法1所示. 算法1.SHSSA算法 输入:搜索空间和目标函数 输出:最优解 1.参数初始化(种群规模N,发现者PD及侦察者SD比例,侦察预警值ST,最大迭代次数T等) 2.根据式(6)生成初始种群 3.计算初始适应度值,并排序,找出当前最优和最劣适应度的麻雀位置 4.fori=1 :T 5. forj=1:PD×N 6.p=-1 + 2×rand 7. 根据式(7)计算发现者位置 8. end for 9. forj=PD×N:N 10. 根据式(3)计算跟随者位置 11. end for 12. 在种群中随机选取SD×N只麻雀作为侦察者 13. forj=1:SD×N 14. 根据式(4)计算侦察者位置 15. end for 16. 计算每只个体适应度值并排序,找到当前最优个体和最劣个体 17. 根据式(12)计算当前最优个体的变异位置 18. 根据式(13)选择是否替换最优麻雀位置 19.end for 算法测试均在Windows 10 64 bit 操作系统、16GB内存的计算机上实现,采用MATLAB 2020a进行仿真实验.基于12个基准测试函数,比较SHSSA与3种基本算法:SCA[18]、WOA[19]、SSA,以及两种改进的麻雀算法:CSSA(只引进本文3.1节混沌初始化)、SSSA(只引进本文3.2节螺旋探索策略)的性能.设置每种算法的种群规模为30,最大迭代次数为500,为了降低随机性干扰,每种算法独立运行30次.SCA和WOA参数设置与原文献一致,SSA、CSSA、SSSA、SHSSA中PD=20%,R2=0.8,SD=20%,螺旋探索策略中b取1.基准测试函数如表1所示,其中F1~F5为单峰函数、F6~F9为多峰函数、F10~F12为固定维度函数. 表1 基准测试函数Table 1 Benchmark function 6种算法优化9个高维测试函数(d=10/30/100)和3个固定测试函数的仿真结果分别如表2和表3所示. 由表2可知,对于单峰函数F1、F3,SHSSA在不同维度下均能找到最优解,而SSSA和CSSA相较于SSA在寻优精度上分别提升了至少190个数量级和2个数量级.对于单峰函数F2、F4,SHSSA虽然在100维时没有找到最优解,但相较于其它5种算法寻优精度仍然提升较大,且标准差为0.对于单峰函数F5,SHSSA在各维度的寻优精度均最高,稳定性最强.对于多峰函数F7、F9,基本SSA就能寻得最优解,且寻优精度和稳定性均优于SCA和WOA.对于多峰函数F6,SHSSA的寻优结果最接近理论最优解.对于多峰函数F8,SHSSA和SSSA的寻优精度相同,且标准差均为0,相较于其它4种算法的求解效果更佳. 表2 高维测试函数优化结果(d=10/30/100)Table 2 Optimization results of high dimensional test function(d=10/30/100) 续表 由表3可知,对于固定维度函数F10,SHSSA和SSSA能够求得最优解,而SCA的寻优精度较差.对于固定维度函数F11,SHSSA和SCA的求解精度最高,最接近理论最优解;CSSA和SSSA相较于SSA的寻优结果有一定提升.对于固定维度函数F12,只有SHSSA能够求得理论最优解,且标准差为0,WOA的寻优精度次之;SSSA和CSSA比SSA的寻优精度更高. 总体而言,SHSSA在求解不同维度优化问题时,寻优精度更高,稳定性更强.引入混沌初始化策略的CSSA在一定程度上提升了SSA的求解性能,而引入螺旋探索策略的SSSA能够较大程度的提高SSA的寻优精度. 表3 固定维度测试函数优化结果Table 3 Optimization results of fixed dimensional test function 图3显示了4个高维测试函数(d=30)和2个固定维度测试函数的迭代收敛曲线图.图中横坐标为迭代次数,纵坐标为30次运行的平均适应度. 对于高维函数,从F1、F2的迭代曲线可知,SSSA相较于SSA在收敛速度和寻优精度上有了很大提升,说明引入螺旋探索策略后,发现者能够带领种群迅速聚集到最优位置附近;SHSSA比SSSA的收敛速度更快,寻优精度更高,说明在加入混合变异后,最优麻雀能够有效跳出局部极值空间,加快算法找到全局最优解的速度.从F8、F9可以看出,SHSSA在迭代50次之前就已经收敛,且收敛精度最高.SSSA的收敛速度略逊于SHSSA,说明混合变异提升了算法的收敛速度. 对于固定维度测试函数,从F10可知,SHSSA迭代300次左右寻得最优解,SSSA在迭代400次左右寻得最优解,两种算法的收敛速度和寻优精度均高于其余4种算法,说明本文改进策略对算法性能提升较大.从F12可以看出,在开始迭代时,CSSA的初始适应度就低于SSA且寻优精度高于SSA,说明ICMIC混沌初始化的麻雀种群质量更高;对比其它5种算法,只有SHSSA能够找到最优解且收敛速度最快,证明了本文改进策略的有效性. 图3 测试函数迭代曲线Fig.3 Iteration curve of test function 时间复杂度是评价算法求解速度的一个重要指标,本文对SHSSA算法进行时间复杂度分析. 假设基本SSA中,种群规模为N,待优化问题的维数为d.初始化阶段的时间复杂度为o(f(d)),发现者位置更新的时间复杂度为o(d),跟随者更新的时间复杂度为o(d),侦察者位置更新的时间复杂度为o(d),则基本SSA的时间复杂度为o(d+f(d)).SHSSA算法在初始阶段,发现者、跟随者和侦察者位置更新阶段的时间复杂度与基本SSA相同,在混合变异阶段的时间复杂度为o(f(d)),则SHSSA算法的时间复杂度为o(d+f(d)). 可见,SHSSA与SSA的时间复杂度相同,表示本文所提改进策略并没有降低算法的求解效率. 最大熵法是一种广受关注的阈值分割算法.图像信息量越大,熵就越大,最大熵算法就是找出一组最佳阈值使得总熵值最大[20].本文采用SHSSA进行多阈值图像分割,即寻找一组解(t0,…,tn)使得熵值最大,相应的适应度函数如下: f{t(1,…,n)*}=argmax{H0+H1+,…,+Hn} (14) 设置种群数量为30,最大迭代次数为100,选取Lena图、Barbara图、Peppers图作为测试图像,仿真对比SSA算法和SHSSA算法的阈值分割效果.每幅图像分别进行30次阈值分割,得到分割结果如表4所示. 由表4可知,SHSSA相较于SSA的分割精度更高且标准差更小.图4为两种算法的三阈值分割图,由图4可知,SHSSA分割后的图像比SSA分割后细节更清晰,信息更完整.图5显示了两种算法的分割迭代曲线,从图中可以看出,SHSSA算法的收敛速度更快,说明SHSSA算法的分割速度更快,是一种更为高效的算法. 表4 测试图像多阈值分割结果Table 4 Multi threshold segmentation results of test image 针对麻雀搜索算法收敛速度慢,易陷入局部最优的缺陷,本文提出一种螺旋探索与自适应混合变异的麻雀搜索算法(SHSSA).通过12个基准测试函数的仿真测试以及在图像分割中应用得出如下结论: 1)ICMIC混沌初始化麻雀种群有效提高了麻雀搜索算法初始种群在空间中的遍历性和均匀性;螺旋探索策略能够改善发现者搜索范围不足,导致寻优精度不够的缺陷;自适应混合变异策略增强了最优麻雀跳出局部极值空间的能力. 2)在12个基准测试函数的仿真测试中,SHSSA算法的寻优精度和收敛速度均高于基本SSA算法,且引入单一策略的CSSA算法和SSSA算法的表现均优于SSA算法.相较于SSA算法,SHSSA算法在多阈值图像分割中的表现更好,能够以更快的分割速度达到良好的分割效果. 图4 测试图像三阈值分割图Fig.4 Three threshold segmentation graph of test image 图5 测试图像迭代曲线Fig.5 Iteration curve of test image 3)下一步可以考虑融合其它智能算法优点,改善算法结构,进一步提升麻雀算法的性能,并将该算法应用于更多实际优化问题中.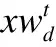
3 螺旋探索与自适应混合变异的麻雀搜索算法
3.1 ICMIC混沌初始化种群
3.2 螺旋探索策略
3.3 基于精英差分和随机反向的自适应混合变异
3.4 SHSSA算法的伪代码
4 算法性能测试
4.1 实验设计
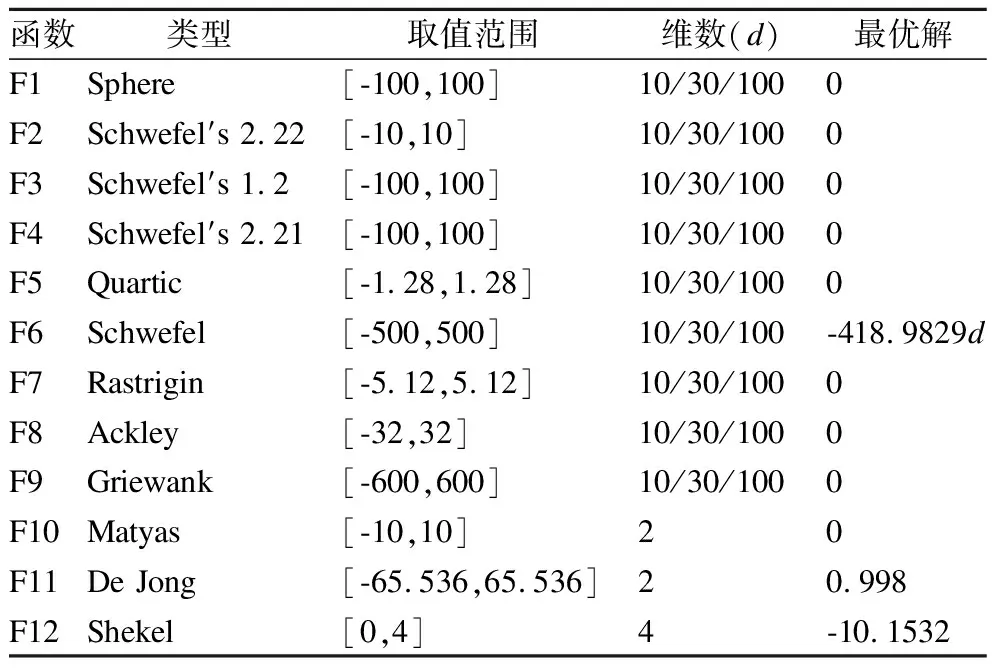
4.2 算法性能对比分析
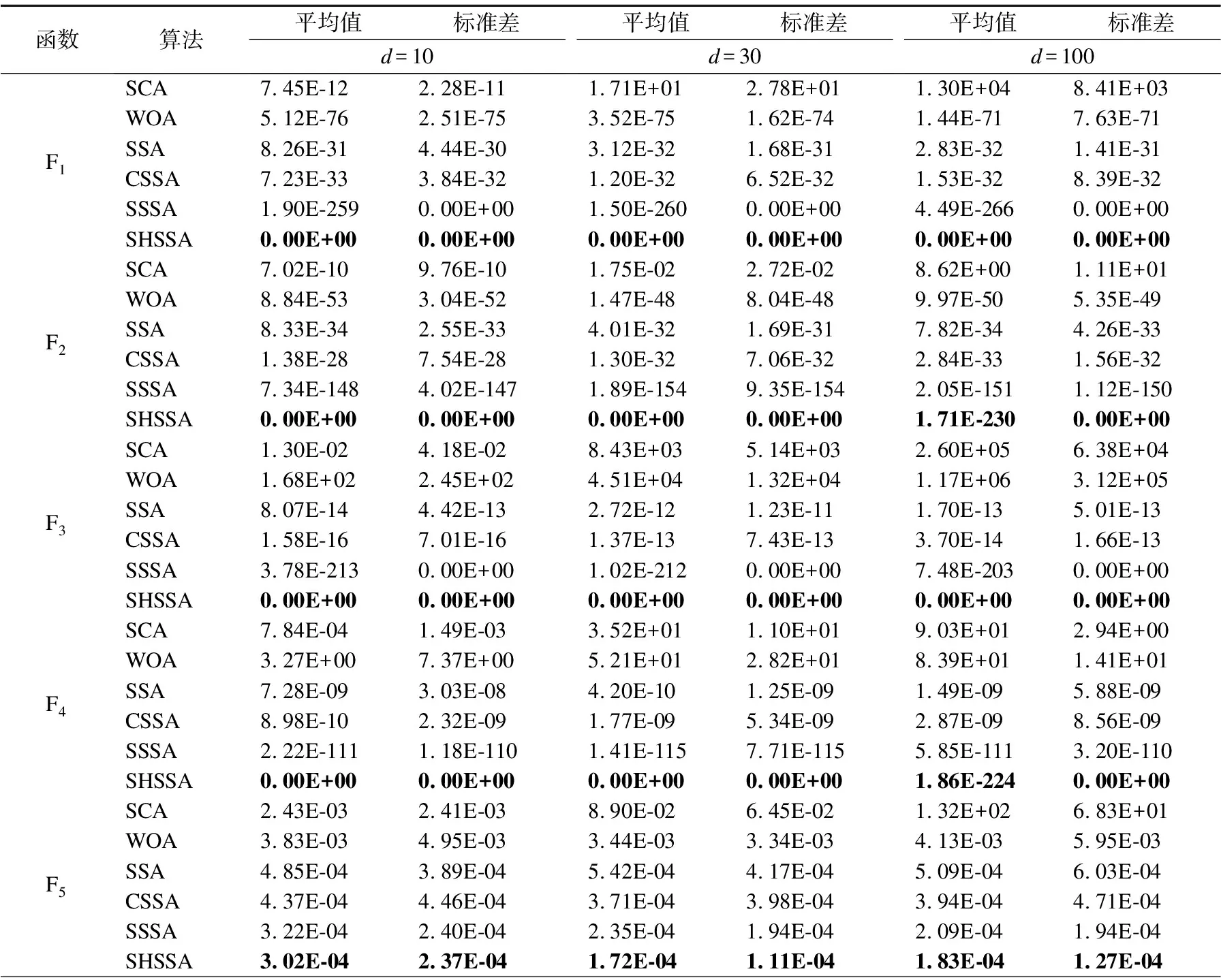
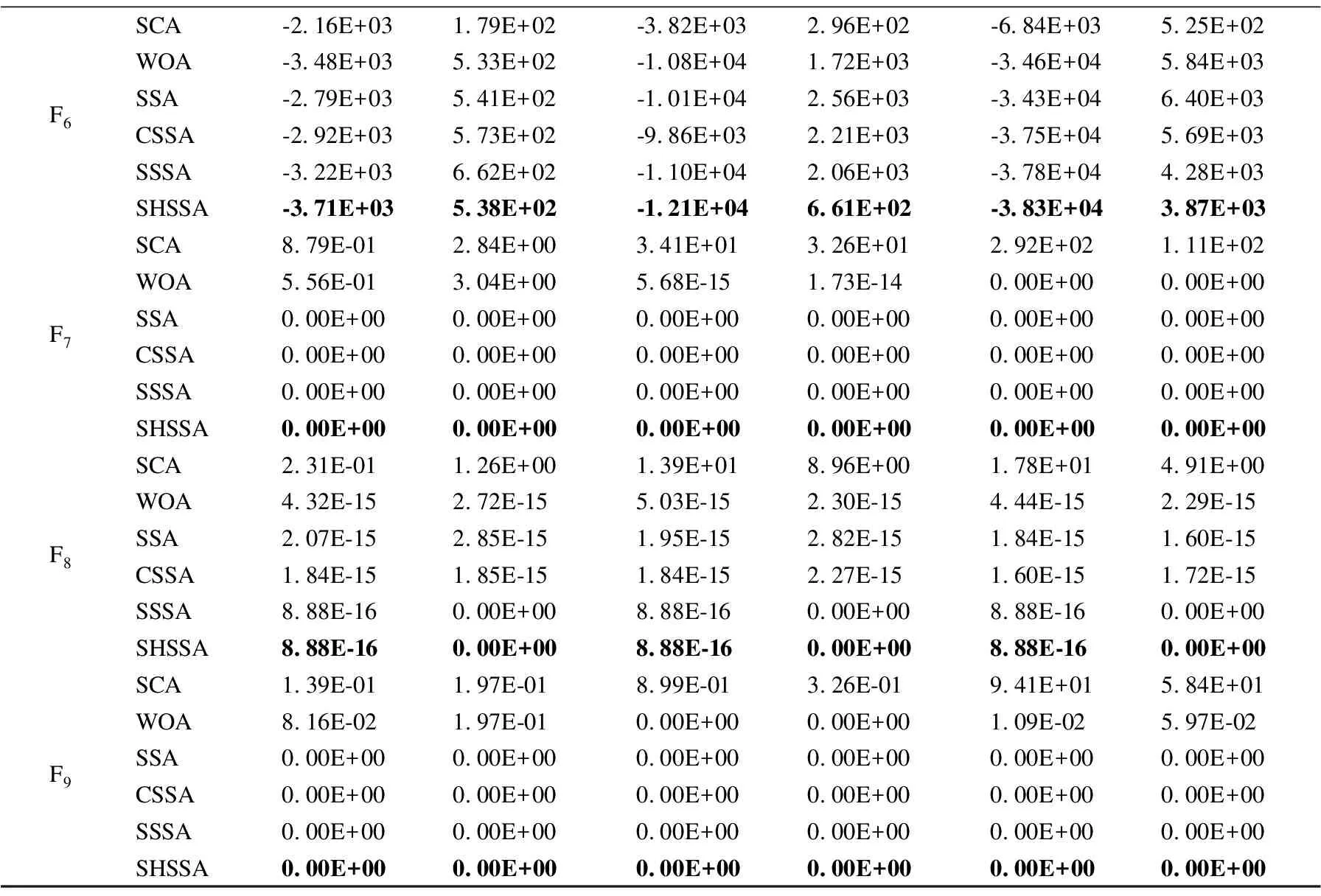

4.3 算法收敛曲线对比分析
4.4 SHSSA算法的时间复杂度分析
5 基于SHSSA的最大熵多阈值图像分割
6 结束语