针对SW26010众核处理器的单精度矩阵乘算法
武 铮,许 乐,安 虹,金 旭,文 可
(中国科学技术大学 计算机科学与技术学院,合肥 230027) E-mail: zhengwu@mail.ustc.edu.cn
1 引 言
矩阵乘是许多关键科学计算算法的核心,包括线性方程组的求解、最小二乘问题、奇异和特征值计算[1],这一本质使得它成为许多科学应用领域的关键高性能kernel之一,包括深度学习、信号处理、天体物理学和先进物理分析等诸多领域[2,3].除此之外,矩阵乘还经常被用于评估针对科学计算的新型处理器架构的性能和效率[4],以及探究如何在新架构上进行高性能优化[5-7].矩阵乘的广泛使用以及计算量稠密且巨大的本质,使得关于它的高性能计算研究一直是学术界和工业界的热门话题之一.
当前矩阵乘性算法的研究主要可以分为两个方面[8],一个是宏观层次的分块方案,基于存储器层次结构,通过合适的矩阵分块策略,探索数据局部性,协调计算和访存的平衡;一个是微观层次的计算kernel,基于高级语言(如:C,C++等)或者底层汇编,通过SIMD运算、指令多发射和乱序执行等微体系结构技术,力求最大化硬件执行单元的计算性能.
在学术界,Kågströ等人[9]最早提出所有的三级BLAS(basic linear algebra subprograms)操作都可以在一个高性能矩阵乘的基础上实现,而现实中许多科学应用都与频繁的稠密线性操作紧密相关,大算力的需求使得众核处理器上的矩阵乘优化一直备受国内外研究学者的关注.Aberdeen等人[10]考虑到Intel Pentium等商用处理器在矩阵乘设计时多级缓存有效使用的困难,针对Intel Pentium III系列处理器详细探究了矩阵乘实现时的寄存器分配以及L1、L2缓存的分块策略,最终平均性能是先进的公开矩阵乘例程的2.09倍.Nakasato[11]在Cypress GPU上优化并实现了单精度和双精度矩阵乘的kernel,分别可以达到理论峰值性能的73%和87%.同时证明了相比于共享内存,纹理缓存对于Cypress架构更有效.Kurzak等人[12]针对Fermi GPU提出了一种通过启发式自动调优生成高效矩阵乘kernel的方法,其搜索空间的修剪机制,可以根据不同的需求很容易地将搜索空间调小或者调大.实验证明其自动生成的kernel可以等同甚至超过cuBLAS和MAGMA,同时在双精度复数的数据类型下有显著的性能提升.Lim等人[13]在矩阵乘分块优化数据重用的基础上,通过数据预取、循环展开和Intel AVX-512优化分块后的矩阵乘,实现了Intel KNL上的高效矩阵乘算法,性能可以与官方最优库Intel MKL相媲美.Lim等人[14]针对Intel KNL和Intel Skylake-SP处理器提出了一种启发式自动调校生成矩阵乘kernel的方法,调校参数包括寄存器级/缓存级的矩阵块大小、预期距离和循环展开深度.结果显示kernel性能优于开源的BLAS库,矩阵乘性能同Intel MKL相当.Chen等人[15]针对GPU架构提出了一种TSM2的矩阵乘算法,主要关注于不规则形状的输入矩阵.该算法在Kepler、Maxwell和Pascal 3种GPU架构上,计算性能加速1.1x~3x,访存带宽提升8%~47.6%,算力利用率提升7%~37.3%.总体来说,学术界当前对于矩阵乘的研究主要集中于通用众核处理器Intel Xeon、Intel Xeon Phi和NVIDIA GPU展开.
在工业界,许多众核处理器厂商提供了便于用户使用的高效BLAS库,比如:Intel的oneMKL[16],NVIDIA的cuBLAS[17],AMD的AOCL[18]等,这些数学库对于使得各自的处理器平台广泛应用于现实世界起到了巨大的推动作用.
申威众核处理器SW26010是世界上第一台峰值运算性能超过100PFlops的超级计算机神威·太湖之光算力的主要贡献者,也是当前众核处理器领域一颗冉冉升起的新星[19].不同于发展历史悠久的通用众核处理器,申威处理器上矩阵乘的研究仍处在初步阶段,现有的研究工作[20-22]也仅仅是对双精度矩阵乘算法设计进行了讨论.然而仅仅针对双精度矩阵乘的研究工作是难以覆盖现实中全部需求的,尤其是近些年迅速发展的人工智能领域,其使用的深度神经网络(deep neural networks,DNNs)技术中单精度矩阵乘是性能的核心[23].另一方面,申威处理器双精度数据运算和单精度数据运算共用双精度浮点运算单元的微体系结构特征,使得单精度矩阵乘算法设计无法直接依赖于双精度矩阵乘的研究工作.
综上所述,为了满足现实生活中人工智能等应用领域的需求,弥补申威处理器SW26010上单精度矩阵乘性能不足的问题,本文主要贡献如下所示:
1) 面向国产申威众核处理器的架构特征,在先前研究工作[22]的基础上,提出了3种基于不同存储层次的并行单精度矩阵乘算法;
2)对于国产申威处理器上的单精度计算过程中数据类型转换的可能情况,从计算层面和访存层面进行了综合讨论,能够为未来该处理器上涉及到单精度计算的研究工作提供有意义的参考借鉴;
3)从峰值性能和通用性两个方面对本文工作进行了综合评估.实验证明,本文设计的算法能够有效提升申威处理器上单精度矩阵乘的性能,其运行时峰值性是理论峰值性能的86.17%,对比最先进的官方库xMath中的实现,提升了6.8%.同时且重要的是,在通用性的实验分析中,相比xMath的实现,在95.33%的场景中能够获得性能提升,最高性能加速比达到247.9%,平均性能加速比为61.66%.
可见本文提出并实现的单精度矩阵乘算法,相比于当前SW26010处理器上的最优实现,不仅能够对不同矩阵乘场景起到更好的适应性,而且性能提升显著.
2 背景介绍
2.1 矩阵乘
BLAS[24,25]有三级子程序,分别是一级的向量-向量操作、二级的矩阵-向量操作和三级的矩阵-矩阵操作.矩阵乘属于三级BLAS,是一个二维数据乘累加的例行程序,如公式(1)所示:
C=αop(A)op(B)+βC,op(X)=XorXT
(1)
其中A∈M×K和B∈K×N为输入矩阵,有转置和不转置两种情况,C=M×N为输出矩阵;α和β是标量,为矩阵乘的运算系数;M、N和K表示矩阵的维度大小.
基础的矩阵乘算法是一个关于M、N和K的三层循环,如算法1所示.其是所有BLAS操作中最关键的部分[26],因为其他多数操作可以依据矩阵乘实现,同时也是最具优化空间的部分,因为它有着最高的计算复杂度O(n3).本文主要面向单精度矩阵乘在申威处理器上的并行算法进行研究,主要目的在于弥补该处理器上单精度研究工作的不足,以及推动其在人工智能领域的发展.
算法1.基础的矩阵乘算法
输入:矩阵A、B和C,矩阵乘系数α和β;
输出:矩阵C.
1. form=0∶1∶Mdo
2. forn=0∶1∶Ndo
3.C[m,n]×=β
4. fork=0∶1∶Kdo
5.C[m,n]+=α(A[m,k]×B[k,n])
6. end for
7. end for
8. end for
2.2 SW26010众核处理器
SW26010处理器[27]是由我国自主研发的一款异构众核处理器,支持64位自主申威指令级系统,采用分布式共享存储和片上计算阵列的异构众核体系架构.
如图1所示,整个处理器包含4个核组(core-group,CG),每个核组由一个主要负责任务管理的主核(management processing element,MPE)和64个主要负责计算任务的从核(computing processing element,CPE)构成,共计260个运算核心.四个核组通过片上网络(network on chip,NoC)互连,每个核组直连一块8GB的DDR3主存,主核和从核通过主存控制器(memory controller,MC)进行相应的访存操作.
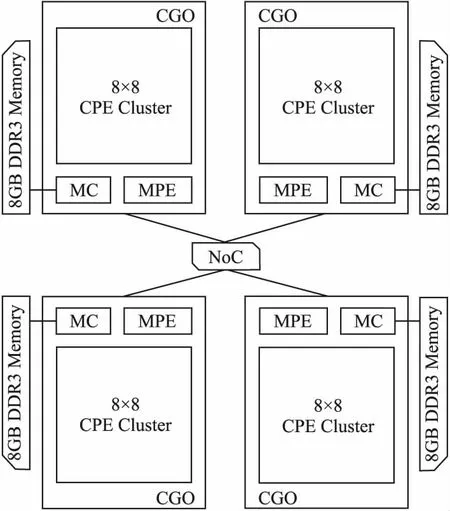
图1 SW26010众核处理器架构Fig.1 Architecture of SW26010 many-core processor
主核拥有L1、L2两级缓存,L1分为32KB的指令缓存和32KB的数据缓存,L2缓存大小为256KB.每个从核配置有一块16KB的L1指令缓存和一块64KB用户可控的局部设备内存(local device memory,LDM).整个从核阵列共享一块大小为64KB的L2指令缓存.
该处理器为了能够尽量简化微架构设计,从而使得有限的芯片面积能够集成更多的计算核心,所以没有采用通用处理器的传统的多级缓存设计方案,而是为每个从核配置了一块64KB的软件控制的片上存储空间LDM.基于此,该处理器支持两种主从核间的数据访问,一种是全局内存访问,也称为gld/gst离散访主存,即是从核直接对主存进行读写操作,这种方式的好处是简单易用,缺陷是访存延迟高达278个时钟周期;一种是以LDM为桥梁进行主存的访问,也称为DMA(direct memory access)批量式访主存,整个过程的访存延迟较低,大约29个时钟周期.但由于LDM大小有限、DMA操作复杂多变等原因导致算法设计难度大,要想获取高性能对开发人员自身体系结构基础要求较高.尽管如此,后者仍是SW26010处理器上研究开发高性能工作的首选.
为尽可能降低访存频率,SW26010处理器为用户提供了单核组从核阵列上不同从核间的数据共享机制——寄存器通信.为了有效支持这一机制,每个从核上配备了发送缓冲区、行接收缓冲区和列接收缓冲区.寄存器通信机制需要注意3点:1) 通信数据的大小固定为256-bits;2) 只能行通信或者列通行;3) 通信的过程是匿名的,基于先到先得的策略接收消息.
最后,SW26010处理器每个从核支持两条硬件流水线P0和P1,其中P0流水支持浮点和整数的标量/向量操作,P1流水支持数据迁移、比较、跳转和整数标量操作.两条流水共享一个指令解码器(Instruction Decoder,ID)和一个指令队列,每个时钟周期ID对队列中前两条指令进行检测,当满足这些情况时,两条指令可以同时被加载到两条流水中:1) 两条指令同已发射未完成的指令不存在冲突;2) 两条指令间不存在(read after write)和(write after write)冲突;3) 两条指令可以分别被两条流水处理.如何混合交差程序中两种类型的指令,使P0和P1两条流水充分并行工作,对于SW26010处理器性能的发挥起着重要的作用.
3 算法设计
不同于通用众核处理器,既支持双精度浮点运算单元,又支持单精度浮点运算单元.申威处理器只具备双精度浮点运算单元,因此在进行单精度运算时,需要显式地或者隐式地进行数据类型转换,以间接完成双精度浮点运算单元计算单精度数据的任务.
基于上述硬件特征,如图2所示,在申威处理器上进行矩阵乘算法设计时,单精度矩阵乘算法有必要在双精度矩阵乘算法实现的基础上,额外地增加一个数据类型转换模块的设计.
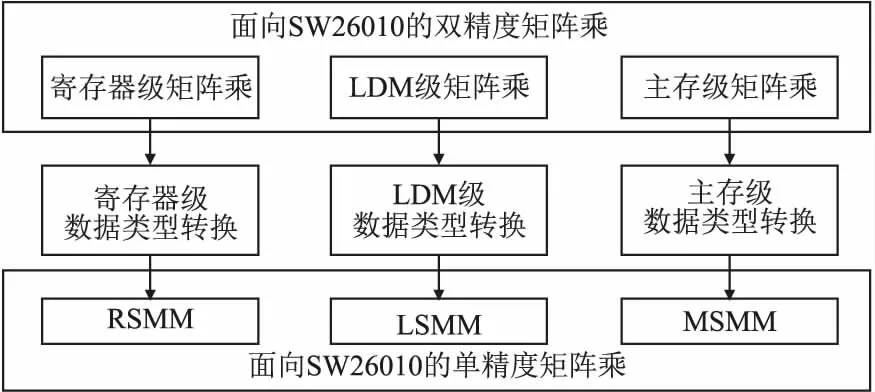
图2 单精度矩阵乘算法设计的基本思想Fig.2 Base idea of single-precision matrix multiplication algorithm
本文将在先前研究工作[22]的基础上,对单精度矩阵乘算法进行深入研究.依据申威处理器的存储器层次结构可以将双精度矩阵乘划分为3个层次,分别是寄存器级的矩阵乘、LDM级的矩阵乘和主存级的矩阵乘,具体实现细节可以参考[22].同理,数据类型转换模块也可以插入到上述3个不同的层次中,分别对应寄存器级的数据类型转换、LDM级的数据类型转换和主存级的数据类型转换,三者的核心区别在于转换后数据的暂存存储空间不同,也由此提出了本文的3种不同的单精度矩阵乘算法——基于寄存器级数据类型转换的单精度矩阵乘,标记为RSMM;基于LDM级数据类型转换的单精度矩阵乘,标记为LSMM;基于主存级数据类型转换的单精度矩阵乘,标记为MSMM.

表1 统一符号声明Table 1 Descriptor of symbols
为了方便后续叙述,本文对相关符号统一声明,如表1所示.
3.1 RSMM
单精度矩阵乘算法最直接的设计方式就是将[22]中所有的双精度操作全部替换为单精度操作,如算法2所示.
算法2.基于寄存器级数据类型转换的单精度矩阵乘算法
输入:矩阵ASM、BSM和CSM,矩阵乘系数α和β;
输出:矩阵CSM.
1.loadAASM[0,0]toASL[cmpt]
2.loadBBSM[0,0]toBSL[cmpt]
3.end loadA
4.end loadB
5.form=0∶1∶mMdo
6. forn=0∶1∶nMdo
7. loadCCSM[m,n] toCSL
8.CSL×=β
9. fork=0∶1∶kMdo
10. computem′,n′,k′of next memory access aboutASMandBSM
11. loadAASM[m′,k′]toASL[ldst]
12. loadBBSM[k′,n′]toBSL[ldst]
13.ASL[cmpt]×=α
14. kernel(ASL[cmpt],BSL[cmpt],CSL)
15. end loadA
16. end loadB
17. exchange the value ofcmptandldst
18. end for
19. storeCCSLtoCSM[m,n]
20. end storeC
21. end for
22.end for
首先对主存上的单精度矩阵数据ASM、BSM和CSM进行分块,分别划分mM×kM、kM×nM和mM×nM个矩阵块.然后将划分后的矩阵块按计算需要依次加载到LDM的单精度矩阵空间ASL、BSL和CSL中,其中ASL又被分为ASL[cmpt]和ASL[ldst],BSL又被分为BSL[cmpt]和BSL[ldst],cmpt和ldst分别用于存放当前计算需要的矩阵块以及下一次计算需要的矩阵块.通过对ASM和BSM矩阵块的加载和核心计算kernel进行一次循环的错开,实现了申威处理器上异步DMA访存操作下的计算和访存的并行.最后更新后的CSL会被写回CSM中对应的主存空间.
因为申威处理器不存在单精度浮点运算单元的缘故,算法2中行14的初始实现如图3左侧所示,ldse和vlds指令包含单精度数据到双精度数据类型的隐式转换过程,前者加载转换单精度ASL并向量扩展到双精度ADR,后者向量加载并转换单精度BSL到双精度BDR,整个计算过程由vmad指令运行于双精度浮点运算单元.此处展示的是RSMM中kernel的最内层循环部分的指令序列,也是指令重排的部分,该循环前的CSL到CDR的转换和循环后的CDR到CSL的转换不在指令重排的考虑范围.
初始情况下整条指令序列的执行时间是60个时钟周期,IPC(instruction per cycle)为0.65,远低于理论值2,造成这一糟糕结果的原因主要有两点——1)P0和P1两条流水线的运行几乎是串行的;2)访存指令(ldse和vlds)和寄存器通信指令(putr和putc)间的数据依赖造成了大量的流水线气泡.为此本文参考[28,29],通过手动重排指令序列,解决上述问题,提升整个指令序列的并行度.整体的重排思想有两点——1)循环交叉适用于P0和P1流水线的指令,尽可能地掩藏向量计算外的其他指令的开销;2)ldse和vlds指令延迟是4个时钟周期[27],通过使具有相关数据依赖的putr和putc指令的理论开始时间滞后至少4个时钟周期,从而消除不必要的流水线气泡.结果如图3右侧所示,重排后指令序列的执行时间是23个时钟周期,IPC约为1.7,性能是初始时的2.61倍.

图3 计算kernel的指令重排Fig.3 Reorder the instructions of the computational kernel
3.2 LSMM
RSMM虽然是最直观的一种双精度矩阵乘映射到单精度矩阵乘的算法,但其计算kernel最内层循环指令重排后的开销高达23个时钟周期,相比于[22]的16个时钟周期,计算性能下降了30.4%.针对这一问题,本文提出了LSMM算法,通过将数据类型转换操作从寄存器转移到片上存储LDM上,从而实现双精度矩阵乘计算kernel的无缝链接.
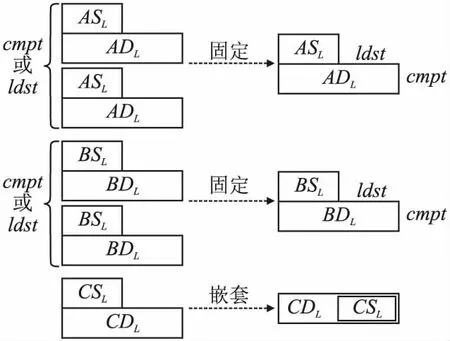
图4 优化LDM空间使用Fig.4 Optimize the usage of the LDM
如图4左侧所示,为每一个ASL、BSL和CSL分别匹配一个双倍大小的ADL、BDL和CDL,用于暂存转换后的双精度数据.此时LSMM相比于RSMM,虽然计算kernel的性能得到了极大的改善,但是却需要额外两倍的LDM开销,这对于申威处理器64KB的有限片上存储来说是难以接受的.为了提高LDM的使用效率,如图4右侧所示,分配一个CDL空间,通过嵌套CSL和CDL,实现两者LDM空间物理上的共用和逻辑上的分离;分配一个ASL/BSL和一个ADL/BDL,固定前者被用于DMA读主存数据,固定后者被用于暂存类型转换后的数据.此时,LSMM的额外LDM开销下降至约60%,整体设计思路如算法3所示.
算法3.基于LDM级数据类型转换的单精度矩阵乘算法
输入:矩阵ASM、BSM和CSM,矩阵乘系数α和β;
输出:矩阵CSM.
1.loadAASM[0,0]toASL
2.loadBBSM[0,0]toBSL
3.end loadA
4.end loadB
5.ADL=(double)(ASL×α)
6.BDL=(double)(BSL)
7.form=0∶1∶mMdo
8. forn=0∶1∶nMdo
9. loadCCSM[m,n]toCSL
10.CDL=(double)(CSL×β)
11. fork=0∶1∶kMdo
12. computem′,n′,k′of next memory access aboutASMandBSM
13. loadAASM[m′,k′]toASL
14. loadBBSM[k′,n′]toCDL
15. kernel(ADL,BDL,BDL)
16. end loadA
17. end loadB
18.ADL=(double)(ASL×α)
19.BDL=(double)(BSL)
20. end for
21.CSL=(float)(CDL)
22. storeCCSLtoCSM[m,n]
23. end storeC
24. end for
25.end for
对于算法3可以概述如下:1)DMA读主存数据和DMA写主存数据都以单精度数据类型进行;2)数据类型转换操作紧邻DMA实时进行,转换结果暂存于LDM;3)计算kernel直接使用转换后的双精度数据.对于CSL和CDL的嵌套,物理上CDL的后半部分也是CSL,从而使得算法3的行10顺序遍历时,不会造成转换后的双精度数据覆盖后续转换所需要的单精度数据的错误.相应的,算法3中行21则要逆序遍历,以保证转换数据的准确性.同时,对于ASL/BSL和ADL/BDL的转换操作需要在DMA读主存数据完成后立即进行,从而闲置ASL/BSL,为下一次的DMA读主存数据做准备.
3.3 MSMM
LSMM虽然保证了计算kernel的高效运行,但数据类型转换的开销仍是不可忽视的.其中,CSM的数据类型转换仅进行了一次,ASM和BSM却分别重复转换了nM次和mM次.由此可见,随着矩阵规模逐渐增大,ASM和BSM的数据类型转换对LSMM性能的影响将会越来越明显.为了解决这一问题,本文提出了MSMM算法,通过消除不必要的数据类型转化操作,进一步提升大规模矩阵乘运算时的性能.
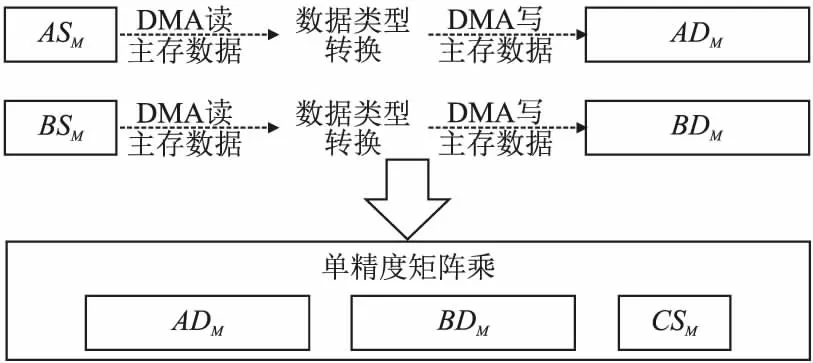
图5 消除不必要的数据类型转换开销Fig.5 Eliminate the unnecessary cost of data type conversion
如图5所示,在主存上为ASM和BSM分别分配一个双倍大小的ADM和BDM,用于暂存转换后的双精度数据.此时MSMM执行包含两个阶段:1)DMA读主存数据ASM和BSM,转换单精度数据到双精度数据,再DMA写回主存ADM和BDM;2)基于ADM、BDM和CSM执行矩阵乘运算.
通过用主存暂存转换后的双精度数据,消除了LSMM中不必要的转换开销.但是此时也在转换阶段引入了新的DMA读主存和DMA写主存操作.为此,本文对MSMM算法进一步优化,如算法4所示.
算法4.基于主存级数据类型转换的单精度矩阵乘算法
输入:矩阵ASM、BSM和CSM,矩阵乘系数α和β;
输出:矩阵CSM.
1.loadAASM[0,0]toASL[cmpt]
2.loadBBSM[0,0]toBSL[cmpt]
3.end loadA
4.end loadB
5.ADL[cmpt]=(double)(ASL[cmpt]×α)
6.BDL[cmpt]=(double)(BSL[cmpt])
7.form=0∶1∶mMdo
8. forn=0∶1∶nMdo
9. loadCCSM[m,n]toCSL
10.CDL=(double)(CSL×β)
11. fork=0∶1∶kMdo
12. computem′,n′,k′of next memory access aboutASMandBSM(ADMandBDM)
13. ifADM[m′,k′]未暂存转换后的结果
14. loadAASM[m′,k′]toASL[ldst]
15. else
16. loadAADM[m′,k′]toADL[ldst]
17. end if
18. ifASM[m,k]转换后的数据未被写回过主存
19. storeAADL[cmpt]toADM[m,k]
20. end if
21. ifBDM[k′,n′]未暂存转换后的结果
22. loadABSM[k′,n′]toBSL[ldst]
23. else
24. loadABDM[k′,n′]toBDL[ldst]
25. end if
26. ifBSM[k,n]转换后的数据未被写回过主存
27. storeBBDL[cmpt]toBDM[k,n]
28. end if
29. kernel(ADL[cmpt],BDL[cmpt],CDL)
30. end loadA
31. end loadB
32. ifADM[m′,k′]未暂存转换后的结果
33.ADL[ldst]=(double)(ASL[ldst]×α)
34. end if
35. ifBDM[k′,n′]未暂存转换后的结果
36.BDL[ldst]=(double)(BSL[ldst])
37. end if
38. ifASM[m,k]转换后的数据未被写回过主存
39. end storeA
40. end if
41. ifBSM[k,n]转换后的数据未被写回过主存
42. end storeB
43. end if
44. exchange the value ofcmptandldst
45. end for
46.CSL=(float)(CDL)
47. storeCCSLtoCSM[m,n]
48. end storeC
49. end for
50.end for
通过将MSMM的数据类型转换阶段和矩阵乘运算阶段融合到一起,双缓冲消除了额外的DMA访存操作.在算法4中,本文在LDM上分配双精度矩阵空间ADL、BDL和CDL,同时将ASL、BSL和CSL分别嵌套在它们的后半部分,从而实现物理上的共用和逻辑上的分离.其中,ADL/BDL又被分为ADL[cmpt]/BDL[cmpt]和ADL[ldst]/BDL[ldst],分别用于存放当前计算需要的矩阵块以及下一次计算需要的矩阵块.类似的,对应的ASL/BSL也被分为ASL[cmpt]/BSL[cmpt]和ASL[ldst]/BSL[ldst].在每次DMA读下一次kernel计算所需的矩阵块ADM[m′,k′]和BDM[k′,n′]时,判断其主存空间中是否已经存入转换好的双精度数据.如果没有,则DMA读ASM[m′,k′]和BSM[k′,n′],并在加载之后转换为双精度数据;如果有,则DMA直接读ADM[m′,k′]和BDM[k′,n′].类似的,在每次计算kernel前,判断当前计算所对应的矩阵块ASM[m,k]和BSM[k,n]转换后的数据是否已经被写回主存.如果没有,则将ADL[cmpt]和BDL[cmpt]写回对应的主存空间ADM[m,k]和BDM[k,n].通过上述操作,本文利用DMA异步技术下计算和访存的双缓冲,尽可能地减少了不必要的访存开销.虽然该算法能够最大化运行时峰值性能,但是却需要额外的双倍ASM+BSM字节大小的主存空间开销.因此,在使用该算法时应考虑到SW26010单芯片主存容量32GB的架构特性.
4 实验结果及分析
4.1 实验设置
本文使用的申威众核处理器SW26010,配置如表2所示.
本文主要在SW26010处理器单核组实现了上述3种不同的单精度矩阵乘算法,因为跨不同核组的并行通常由更高编程级别的用户自己处理.对比对象为该平台上最先进的官方数学库xMath中的单精度矩阵乘,标记为SWSMM.后续将针对两个方面进行实验设计和结果分析,一个是峰值性能,一个是通用性,前者反映了本文工作在硬件资源上发挥出的最大利用率,后者验证了本文工作能否更好地应用于现实世界中多变的矩阵乘配置.
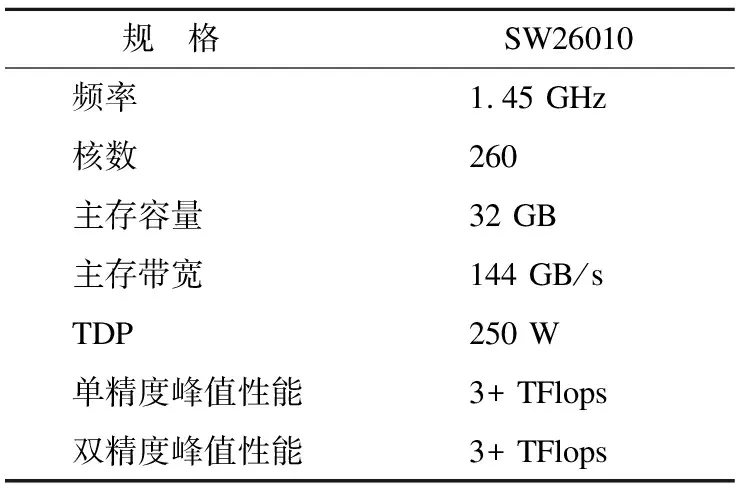
表2 SW26010配置参数Table 2 Configure parameters for SW26010
本文所有测试均是迭代10次,去掉一个最优值和最差值,取剩余测试结果的平均值.
4.2 峰值性能测试
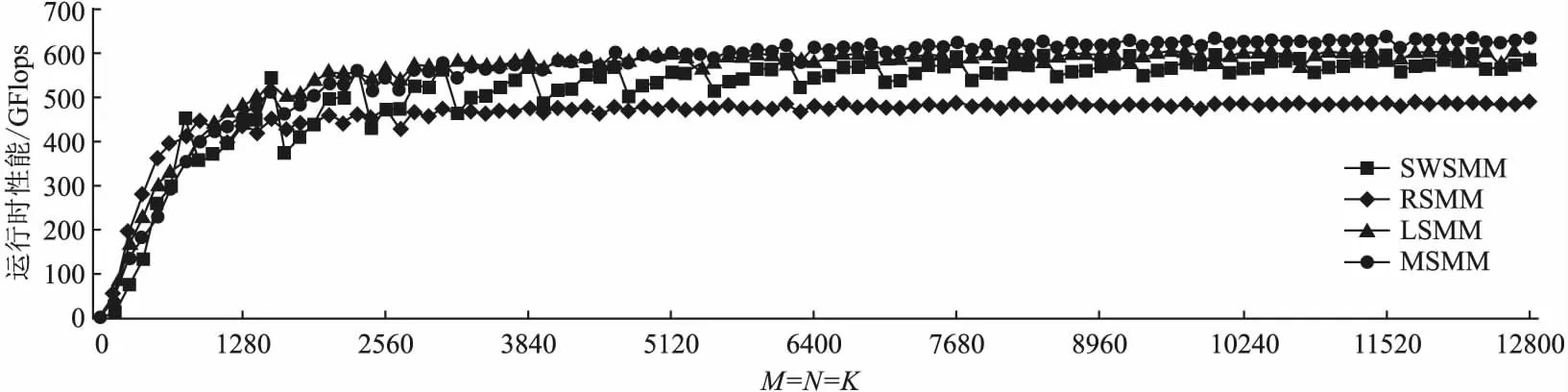
图6 申威处理器上不同单精度矩阵乘实现的运行时峰值性能比较Fig.6 Peak performance comparison of different single-precision matrix multiplication implementations on SW26010
方阵(M=N=K)是矩阵乘运行时峰值性能测试的最佳选择,因此本文选取M=N=K=128X,其中X=1,2,…,100,共100组不同的矩阵乘配置测试.
如图6所示,用当前最先进的单精度矩阵乘实现SWSMM对比本文提出的3种算法RSMM、LSMM和MSMM.其中,SWSMM的最高性能可以达到598.85GFlops,而RSMM、LSMM和MSMM分别可以达到489.03GFlops、609.11GFlops和639.66GFlops.RSMM远低于SWSMM,主要原因是计算kernel指令执行周期更长,限制了运行时的峰值性能;LSMM与SWSMM较为接近,可以猜想两者的实现原理大致相同;MSMM则明显高于SWSMM,可见其极大地降低了大规模单精度矩阵乘中数据类型转换的开销.
单独对比本文提出的3种算法RSMM、LSMM和SWSMM,从图6可以看出,当方阵规模在896以内时,RSMM性能较高;随着规模的增加,LSMM性能变得更为突出;最后当规模达到4608之后,MSMM的性能基本最优.这是因为随着方阵规模的增加,访存的影响逐渐减小,计算kernel的影响逐渐增大,这使得小规模时RSMM较优;反之,LSMM的性能更好,这是因为LSMM是以额外的LDM占用来换取更高的性能.LSMM和MSMM计算kernel相同,但是随着方阵规模的再度增加,数据类型转换的影响越发突出,这也使得MSMM的性能优势开始凸显.
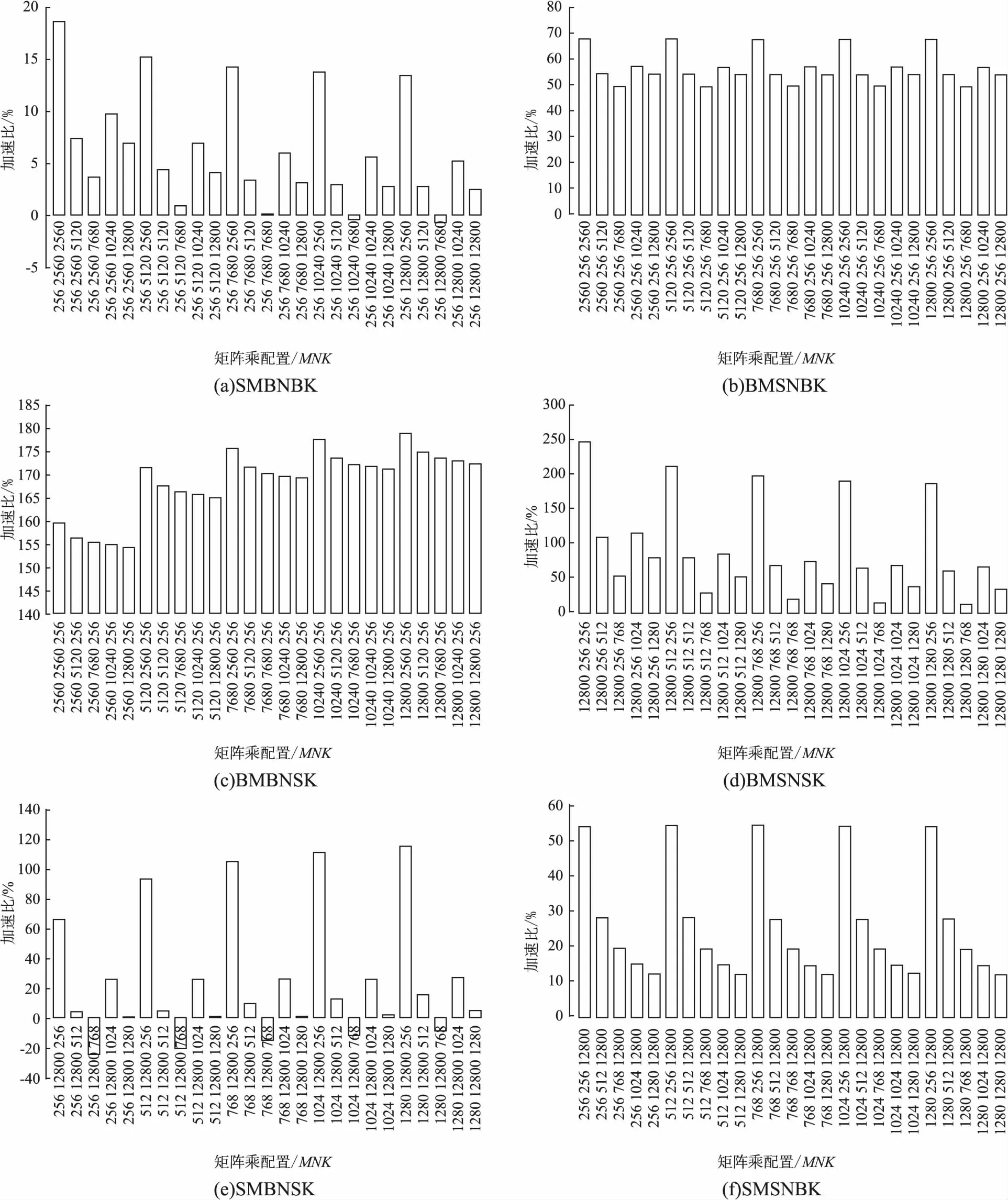
图7 不同矩阵乘配置的性能加速比Fig.7 Speedup of different matrix multiplication configurations
最终本文工作最高可以发挥申威处理器单精度理论峰值性能的86.17%,相比于SWSMM的运行时峰值性能提升了6.8%.同时,从图6性能的变化趋势中,可以看出本文工作实现的单精度矩阵乘性能波动较小,稳定性更好.
4.3 通用性测试
矩阵形状的不同使得矩阵乘在现实世界中也是多种多样的,依据M、N和K相对大小的不同,可以分为8种不同的类型,标记为BMBNBK、SMSNSK、SMBNBK、BMSNBK、BMBNSK、BMSNSK、SMBNSK和SMSNBK.‘B’表示相对值小,‘S’表示相对值大,举例说明:SMBNBK就表示小M大N大K的矩阵乘.在3.2节中方阵的测试,代表着BMBNBK和SMSNSK两种场景,但是比起方阵这种矩阵乘,剩余的6种长条形矩阵乘场景更为普遍.本节以SWSMM为基准,SMBNBK等6种场景各取25例,测试并分析本文工作在各个矩阵乘配置下的最优加速比.
如图7所示,从单类场景来看,BMSNBK、BMBNSK、BMSNSK和SMSNBK中,本文工作相比SWSMM在所有的矩阵乘测试中都具有明显性能提升,最低提升分别为49.49%、154.53%、12.93%和12.1%,最高提升分别为67.73%、179.02%、247.9%和54.43.
SMBNBK和SMBNSK是存在性能下降的两类场景,而造成这一现象的主要原因很可能是由于在某些情况下本文算法的矩阵乘分块方式不够完善,没有发挥算法的最大潜力,使得其性能略低于SWSMM.这两种场景虽然都有性能下降的情况,但是无论在程度还是数量上都远远低于性能提升的情况,两者最差时性能分别下降0.7%和23.5%,而性能最优时分别提升18.6%和116%,且性能提升的情况在数量上分别占据92%和80%.所有场景来看,平均性能提升达到了61.66%,并在95.33%的情况下性能更高.由此可见,本文工作因既考虑了计算层面的优化技术又兼顾了访存层面的优化技术,从而相比SWSMM不仅性能提升显著,而且通用性更强.
5 总 结
随着我国自主研发的申威众核处理器SW26010在科学计算和人工智能领域的快速发展,对于该众核处理器上高性能矩阵乘算法实现提出了更高的要求.而现有的关于矩阵乘的研究工作寥寥无几,仅有的工作也仅仅是针对双精度矩阵乘算法的讨论.考虑到SW26010特有的架构特征——双精度数据运算和单精度数据运算共用双精度浮点运算单元,使得单精度矩阵乘算法直接套用双精度矩阵乘算法难以充分发挥该处理器的硬件性能.本文针对上述问题,结合SW26010的体系结构特征,提出了3种不同存储层次的单精度矩阵乘并行算法,分别是RSMM、LSMM和MSMM.在进行算法设计时,综合考虑了计算和访存两个核心因素,在计算方面,结合该处理器的从核双流水,从汇编层面手动控制核心计算任务的指令序列,保证了高效的指令级并行;在访存方面,综合考虑了有限片上存储资源的有效使用,以及访存任务和计算任务的交叉并行.在实验分析中,以当前最先进的官方库xMath中的实现SWSMM作为基准,从峰值性能和通用性两个方面进行测试分析,最终证明本文工作不仅能够不同程度上提升单精度矩阵乘运算的性能,而且对于不同的矩阵乘场景也有着更好的适应性.
下一步将重点研究本文优化算法同人工智能应用的具体结合,从而探索申威众核处理上的深度学习并行优化技术.

