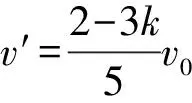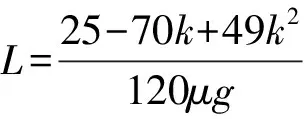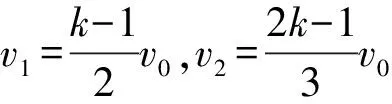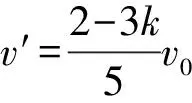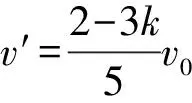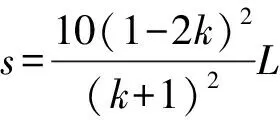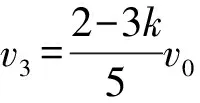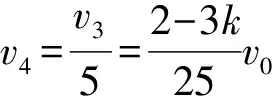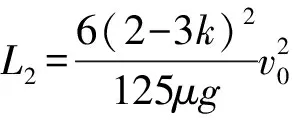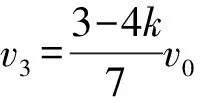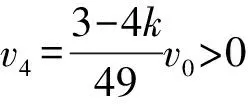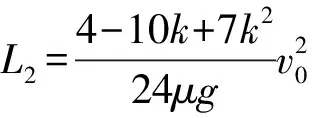基于2022年河北省新高考物理试卷第13题的作业设计

张 伟

(河北省沧州市第十中学)

【例题】如图1,光滑水平面上有两个等高且足够长的滑板A和B,质量分别为1 kg和2 kg,A右端和B左端分别放置物块C和D,物块质量均为1 kg,A和C以相同速度v0=10 m/s向右运动,B和D以相同速度kv0向左运动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新物块,A与B粘在一起形成一个新滑板,物块与滑板之间的动摩擦因数均为μ=0.1。重力加速度大小取g=10 m/s2。求:

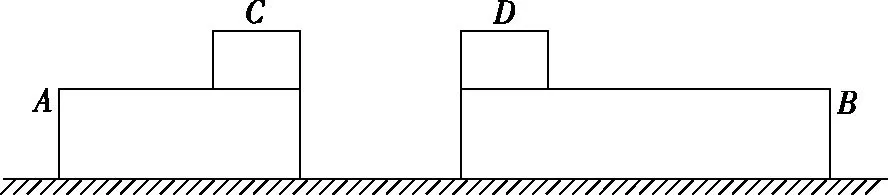
图1

(1)若0

(2)若k=0.5,从碰撞后到新物块与新滑板相对静止过程两者相对位移的大小。

【解题思路】

(1)根据动量守恒定律得出新物块和新滑板的速度大小和方向。

(2)先分析出新物块和新滑板的速度,结合运动学公式、动量守恒定律和能量守恒定律分析出相对位移的大小。

【解析】(1)物块C、D碰撞过程中满足动量守恒,设碰撞后物块C、D形成的新物块的速度为v1,C、D的质量均为m=1 kg,以向右为正方向,则mv0-m·kv0=(m+m)v1

可知碰撞后物块C、D形成的新物块的速度大小为5(1-k)m/s,方向向右

滑板A、B碰撞过程中满足动量守恒,设碰撞后滑板A、B形成的新滑板的速度为v2,滑板A和B质量分别为1 kg和2 kg,则有

Mv0-2M·kv0=(M+2M)v2

则新滑板速度方向也向右

(2)若k=0.5,可知碰后C、D形成的新物块的速度为

碰后瞬间滑板A、B形成的新滑板的速度为

可知碰后新物块相对于新滑板向右运动,新物块向右做匀减速运动,新滑板向右做匀加速运动,新物块的质量为m′=2 kg,新滑板的质量为M′=3 kg,相对静止时的共同速度为v共,根据动量守恒定律可得

解得v共=1 m/s

根据能量守恒定律可得

解得x相=1.875 m

本题考查动量守恒定律和能量守恒定律的应用,根据动量守恒定律分析出物块的速度,结合能量守恒定律得出相对位移,综合性较强。

【学习新课作业设计】

1.如图1所示,光滑水平面上有两个等高且足够长的滑板A和B,质量分别为m1和2m1,A右端和B左端分别放置物块C、D,物块质量均为m0,A和C以相同速度v0向右运动,B和D以相同速度kv0(k>0)向左运动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新物块,A与B粘在一起形成一个新滑板,物块与滑板之间的动摩擦因数均为μ,重力加速度大小取g。

请讨论k取不同的值时,刚发生碰撞之后新物块和新滑板的运动情况。

剖析:此题可以让初学者对动量守恒定律的系统性和方向性有一个深入的认识,要想应用动量守恒定律,首先应该选择满足动量守恒条件的系统作为研究对象,譬如此题我们应该选A和B作为一个系统,C和D作为一个系统。碰撞瞬间内力远远大于外力,系统动量守恒。同时动量是矢量,动量守恒定律的表达式是矢量表达式,列式之前首先要选定正方向,若列式求解出的速度为正,则表示物体向选定的正方向运动,反之则向反方向运动。

【解析】选取C和D作为一个系统,设碰后瞬间新物块速度为v1,以向右为正方向。根据动量守恒定律可得m0v0-m0·kv0=2m0v1

当k=1时,v1=0表示碰后瞬间新物块速度是零(但不会静止)

当k<1时,v1>0表示新物块向右运动

当k>1时,v1<0表示新物块向左运动

然后选取A和B作为一个系统,设碰后瞬间新滑板速度为v2,以向右为正方向。根据动量守恒定律可得m1v0-2m1·kv0=(m1+2m1)v2

当k=0.5时,v2=0表示碰后瞬间新滑板速度是零(但不会静止)

当k<0.5时,v2>0表示新滑板向右运动

当k>0.5时,v2<0表示新滑板向左运动

综合可得

当k<0.5时,二者均向右运动

当k=0.5时,碰后瞬间新滑板速度是零,新物块向右运动

当0.5

当k=1时,碰后瞬间新物块速度是零,新滑板向左运动

当k>1时,二者均向左运动

【一轮综合习题设计】

2.如图1所示,光滑水平面上有两个等高且足够长的滑板A和B,质量分别为m0和2m0,A右端和B左端分别放置可视为质点的物块C、D,两物块下方与滑板接触处均匀涂抹了新鲜墨汁,物块质量均为m0,A和C以相同速度v0向右运动,B和D以相同速度kv0(k>0)向左运动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新物块,A与B粘在一起形成一个新滑板,物块与滑板之间的动摩擦因数均为μ,重力加速度大小为g。求:当k取不同的值时,从碰撞后到新物块与新滑板相对静止时,新滑板上留下的墨迹长度。

剖析:新滑板上留下的墨迹长度就等于新物块与新滑板相对滑动时最大相对位移的大小。是一个典型的应用动量守恒定律和能量守恒定律联合解决的问题。

【解析】选取C和D作为一个系统,设碰后瞬间新物块速度为v1

以向右为正方向。根据动量守恒定律可得

m0v0-m0·kv0=2m0v1

然后选取A和B作为一个系统,设碰后瞬间新滑板速度为v2

以向右为正方向。根据动量守恒定律可得

m0v0-2m0·kv0=(m0+2m0)v2

针对新物块和新滑板组成的系统应用动量守恒定律可得

2m0v1+3m0v2=5m0v′ ①

设新滑板上留下的墨迹长度为L

针对新物块和新滑板组成的系统应用能量守恒定律可得

【答疑】(1)可以代入特定值验证

与代入上面答案得出结果一致。

(2)当k<0.5时,碰后新物块和新滑板一起向右运动,

所以v1>v2

说明:刚碰完之后新物块比新滑板运动得快,发生相对滑动,新物块在新滑板留下墨迹,然后新物块减速,新滑板加速,达到共速时不再产生新墨迹。

(3)当0.5

针对新物块和新滑板组成的系统应用动量守恒定律可得

2m0v1-3m0v2=5m0v′

针对新物块和新滑板组成的系统应用能量守恒定律可得

这里注意,动量守恒定律的表达式是矢量表达式,此时应该仍然按2m0v1+3m0v2=5m0v′这样列式。

(4)当k>1时,二者均向左运动,以向左为正方向

针对新物块和新滑板组成的系统应用动量守恒定律可得

2m0v1+3m0v2=5m0v′

【总结】无论k取任何值,解析中的答案都是正确的。也就是说,当我们从题设中无法获知物体运动方向时,应用动量守恒定律时,应该用矢量表达式列式。

【二轮提高习题设计】

(1)从k的不同取值范围出发,分别确定新物块与新滑板最终的速度大小和方向。

(2)如果v0是未知量,

【解析】(1)选取C和D作为一个系统,设碰后瞬间新物块速度为v1

以向右为正方向。根据动量守恒定律可得

m0v0-m0kv0=2m0v1①

然后选取A和B作为一个系统,设碰后瞬间新滑板速度为v2

以向右为正方向。根据动量守恒定律可得

m0v0-2m0kv0=(m0+2m0)v2②

针对新物块和新滑板组成的系统应用动量守恒定律可得

2m0v1+3m0v2=5m0v′ ③

针对新物块和新滑板组成的系统应用能量守恒定律可得

【考前冲刺强化训练】

4.如图2所示,光滑水平面上有两个等高的滑板A和B,质量分别为m0和2m0,A右端和B左端分别放置物块C、D,物块质量均为m0,A和C以相同速度v0向右运动,B和D以相同速度kv0(k>0)向左运动,在某时刻发生碰撞,作用时间极短,碰撞后C与D粘在一起形成一个新物块,A与B粘在一起形成一个新滑板,物块与滑板之间的动摩擦因数均为μ,重力加速度大小取g。如果滑板足够长,右侧墙壁距离滑板足够远,

图2

(1)求k的取值在什么范围内新滑板可以和墙壁相撞;

(2)如果新滑板与墙壁碰撞时间极短,且新滑板碰后速度大小不变,方向与原来相反,求新物块在新滑板上滑过的距离。

【解析】(1)如果新滑板能与墙壁相撞,则新物块与新滑板共速时速度v3应该向右,以向右为正方向,针对两个物块与两个滑板组成的系统应用动量守恒定律可得

(m0+m0)v0-(2m0+m0)kv0=(3m0+2m0)v3

同时v3>0

(2)新物块在新滑板上滑动可以分成两个过程,一是从刚生成新物块和新滑板到二者达到共速,设新物块在新滑板上滑过的距离为L1;二是从新滑板与墙壁碰撞后到新物块与新滑板达到共速,设新物块在新滑板上滑过的距离为L2,新物块在新滑板上滑过的距离应该为二者之和。

选取C和D作为一个系统,设碰后瞬间新物块速度为v1

以向右为正方向。根据动量守恒定律可得

m0v0-m0kv0=2m0v1

然后选取A和B作为一个系统,设碰后瞬间新滑板速度为v2

以向右为正方向。根据动量守恒定律可得

m0v0-2m0kv0=(m0+2m0)v2

刚生成新物块和新滑板之后到二者达到共速,针对新物块和新滑板组成的系统应用能量守恒定律可得

新滑板与墙壁碰撞时间极短,新物块在碰撞瞬间速度不变,新滑板碰后速度大小不变,方向与原来相反

设新滑板与墙壁碰撞后,新滑板与新物块达共速时速度为v4

以向左为正方向,由动量守恒定律可得

3m0v3-2m0v3=5m0v4

说明:新滑板与新物块达到共速时向左运动,不可能与墙壁再次相撞。

从新滑板与墙壁碰撞后到新物块与新滑板达到共速,针对新物块和新滑板组成的系统应用能量守恒定律可得

新物块在新滑板上滑过的距离为

如果滑板足够长,右侧墙壁距离滑板足够远,且新滑板与墙壁碰撞时间极短,碰后速度大小不变,方向与原来相反,求:

(1)新滑板第一次与墙壁碰撞后向左运动的最大距离;

(2)新滑板第二次与墙壁碰撞前瞬间的速度;

(3)为使新物块始终不会滑离新滑板,滑板B的长度至少是多少?

【解析】(1)如果新滑板能与墙壁相撞,则新物块与新滑板达共速时速度v3应该向右

以向右为正方向,针对两个物块与两个滑板组成的系统应用动量守恒定律有

(2m0+m0)v0-(2m0+2m0)kv0=(4m0+3m0)v3

新滑板第一次与墙壁碰撞后向左做减速运动,当速度减小为零之后反向加速,所以当其速度减小为零时向左运动的距离最大。

设向左运动的最大距离为L1。针对新滑板应用动能定理可得

(2)新滑板第一次与墙壁碰撞后向左运动,新物块继续向右运动

设第一次达共速时速度为v4,以向右为正方向

在此过程应用动量守恒定律可得

4m0v3-3m0v3=7m0v4

(3)为使新物块始终不会滑离新滑板,滑板B的长度至少等于新物块相对滑板滑过的距离L2

首先选取C和D作为一个系统,设碰后瞬间新物块速度为v1

以向右为正方向。根据动量守恒定律可得

2m0v0-2m0kv0=4m0v1

然后选取A和B作为一个系统,设碰后瞬间新滑板速度为v2

以向右为正方向。根据动量守恒定律可得

m0v0-2m0kv0=(m0+2m0)v2

针对形成新物块与新滑板到二者最终停止的过程中,新物块和新滑板组成的系统应用能量守恒定律可得