与二次函数相关的最值问题求解策略
甘肃省甘谷县西关中学
王彩兰
对于与二次函数相关的线段最值问题的考查,往往涉及到的知识点主要有以下几点:其一是两点之间线段最短;其二是垂线段最短;其三是三角形三边关系等内容.如何针对这一考点引导学生对“动”和“定”之间的关系进行思考研究,处理问题中运动变化关系与几何元素的位置、数量关系,提升学生的解题能力和识别能力,从而落实相关的探究活动过程,真正实现数学核心素养要求?本文中结合常见的几种类型作简单的说明.
1 求动点到直线距离的最值:建立二次函数
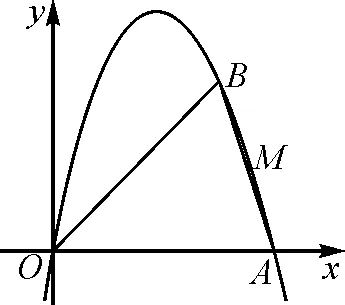
例1如图1,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,OA=OC=3,顶点为D.在AC下方的抛物线上有一点P,过点P作PH⊥AC于点H,求线段PH的最大值及此时点P的坐标.
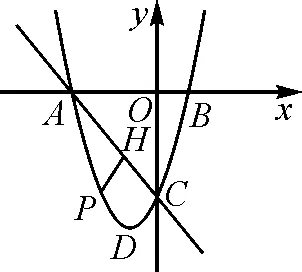
图1
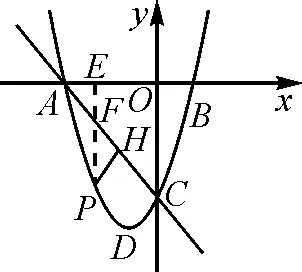
图2
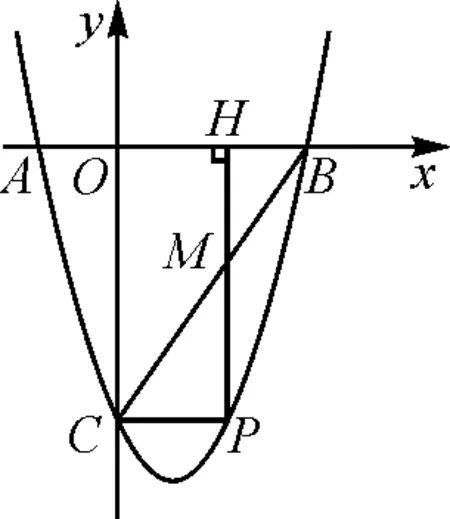
图3
如图2,我们可以过点P作PE垂直x轴于点E,交直线AC于点F.根据直线AC的解析式判断其与x轴的夹角,从而确定PF与PH的关系,结合点P在二次函数上,可以直接写出线段PF的函数关系式,建立二次函数,利用二次函数求解最值,问题得到解决.
再如:如图3,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,-3).若P是第四象限内这个二次函数的图象上任意一点,PH垂直x轴于点H,与BC交于点M,连接PC.求线段PM的最大值.
这道题可以根据平行于y轴的直线上两点间的距离是较大的纵坐标与较小的纵坐标的差,可得二次函数,进而根据二次函数的性质,可得答案.
2 求动点与其他两定点组成的三角形周长的最值:建立“将军饮马”模型
例2如图4,已知二次函数y=ax2+bx+c的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,-3).在其对称轴上确定一点P,使得△BCP的周长最小,试求周长的最小值和点P的坐标.

图4

图5
要使△BCP的周长最小,因为点B和点C固定,BC为定长,则只要PB+PC最小即可.如图5,由于点A与点B关于对称轴对称,从而连接AC交对称轴于点P,则PA+PC=PB+PC=AC,根据两点之间,线段最短,可得PB+PC的最小值,故可求△ABP周长的最小值.本题在处理三角形周长最小值的过程中,将PB+PC转化为“将军饮马”模型进行研究,从而将问题转化为“两点之间线段最短”问题即可得到解决.

图6
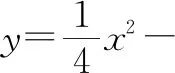
3 求动点到两定点距离之差的最值:转化为三点共线问题
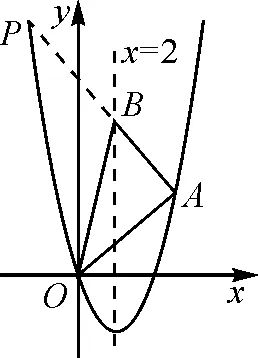
图7
例3如图7,已知抛物线过点O(0,0),A(5,5),且它的对称轴为x=2.点B是抛物线对称轴上的一点,且点B的坐标为(2,8),若P是抛物线上的动点,当PA-PB的值最大时,求点P的坐标以及PA-PB的最大值.

图8
如何探求其差最大呢?我们
不妨建立新的图形进行研究.如图8所示,连接AB并延长,交x轴于点P,任取一点P′,连接AP′,BP′,在△ABP′中,根据三角形的性质,两边之差小于第三边,即AP′-BP′ 对于例3,运用待定系数法可求得直线AB的解析式为y=-x+10,当PA-PB的值最大时,点A,B,P在同一条直线上,联立方程组求解即可求得点P的坐标,利用两点间距离公式可求得AB,即PA-PB的最大值. 此类问题往往考查“抛物线上是否存在一动点,使之与一条定线段构成的三角形面积最大”,这类问题我们也可以简称为“一定两动”求面积最值问题.解答过程中可以先利用两点间的距离公式求出定线段的长度,然后利用抛物线上动点到该线段的距离确定最大值,之后再利用三角形的面积公式即可确定其最大值,在求解过程中,切点即为符合题意的点.当然也可以将所求三角形分割成两个基本模型的三角形,根据切割后三角形的底和高的情况进行求解,这种方法常常会通过二次函数表示,根据二次函数最值求解即可得到. 图9 例4如图9,二次函数y=-x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于点C.在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大?若存在,求出此时点M的坐标;若不存在,请简要说明理由. 图10 图11 例5如图11,在平面直角坐标系中,二次函数y=ax2+bx的图象经过A(5,0),B(4,4).在第一象限的抛物线上存在点M,使以O,A,B,M为顶点的四边形面积最大,求点M的坐标. 根据题意可知,以O,A,B,M为顶点的四边形中,△OAB的面积固定,如图12,因此只要另外一个三角形面积最大,则四边形面积即最大.求出另一个三角形面积的表达式,利用二次函数的性质确定其最值即可.显然,本题中四点所构成的四边形,因点M的位置不确定,故可根据情况进行分类讨论:当0 图12 图13 根据上述内容,我们可以在探究几何模型过程中挖掘求线段最值问题图形的本质,再结合相关内容涉及到的最基本的原理、法则,将多种问题转化为同一类问题来解答,实现方法、思路归一的结果.同时在计算过程中引导学生感悟化归转化、数形结合及函数、方程建模的应用,从而将各种方法灵活运用于问题探究过程中.4 “一定两动”三角形面积的最值:定底求高转化为线段最值
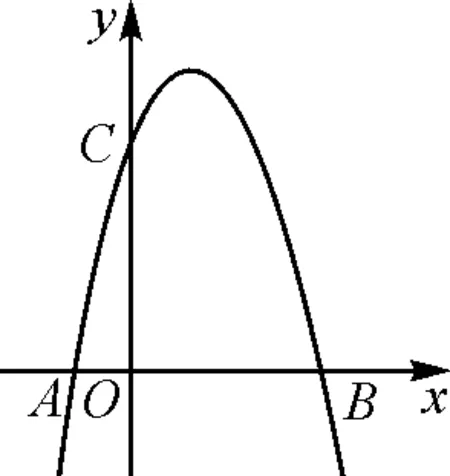
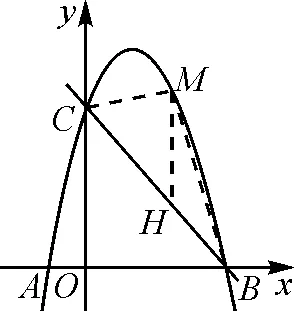
5 “两定两动”四边形面积的最值:转化为三角形求解