初中数学非标准题型解题思路研究
——以“换元法”为例
福建省南安市侨光中学
郑海萍
学生在日常解题中,一旦遇到非标准、非典型的题目,如果按照传统解题思路和模式进行解题,就会处处碰壁,出现甚至解题错误等情况.教师应指导学生另辟蹊径,引入一个或若干个新元素替代问题中的“元”,借助变量代换的方式,通过化繁为简、化难为易,逐渐降低解题难度.同时,鉴于换元法的特点,学生在学习和应用中,也逐渐拓展了自身的解题思路,培养了创新意识,促进了数学核心素养的发展.
1 换元法概述
换元法又称为“辅助元素法”“变量代换法”,主要是运用一个新的变量,代替原本题目中的某一个元素,即运用一个新的元素,代替问题中原来的“元素”,进而使得原本非标准、非典型的数学问题变得更加标准、典型,有效降低学生的解题难度.从本质内涵上来说,换元法就是变量代换、转化,其关键就在于合理选择出“新元”,并将其代入到数学问题中,进行适当的代换,促进数学问题的转化,以便于快速找到解题思路,顺利解决数学问题.
纵观初中数学解题现状,在实施“换元法”时,基本上都是遵循“换元—求解—检验”步骤进行的.常用的换元方法主要包括局部换元、三角换元、均值换元三种.其中,局部换元就是指在数学解题中,某一个代数式反复出现了几次,可采用一个字母进行代替,促使繁杂问题简单化.通常,这一换元方式应用于不等式问题的求解中;三角换元则是在解决去根号、变换为三角形的问题中,运用已知代数式和三角知识间的内在连接点进行换元,常常将函数问题转化为学生熟悉的三角函数进行解答;均值换元则常常应用于“两个未知量的和是已知”的情况,借助均值换元的模式,运用新的变量将两个未知量表示出来,进而完成数学问题的解答[1].
2 换元法在初中数学非标准题型解题中的具体运用
2.1 运用换元法解决方程问题
在初中数学解题中,换元是一种常用的解题方法.尤其是解决一些复杂的方程问题时,如果按照常规的解题方式,问题就会变得非常复杂,甚至超出学生的能力范围,致使学生难以解答.其实,这些题目中常常蕴含着换元的条件,如果对其仔细分析,找出可替换的“元”,并运用新的未知数进行代替,那么,原本复杂的方程问题会变得简单,以便于学生快速解出正确答案.
例1解方程(x2+5x+4)(x2+5x+6)=1.
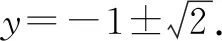
如此一来,例1通过换元法的应用,避免了高次方程的出现,排除了学生无法解决问题的困扰,真正提升了学生的解题效率.学生经过一段时间训练之后,也能从换元解题中,感受到换元法的内涵,唤醒学生的数学解题动机[2].
2.2 运用换元法解决方程组问题
在初中数学解题中,如果方程组求解的难度相对比较高,学生无法按照常规的方式解决时,就可引导学生借助换元法,将原本复杂的方程组进行转化,比如将高次方程组转化为低次方程组.另外,在解方程组的过程中,有的方程组虽然可运用传统的方式解答,但计算量比较大,学生在繁琐的计算中,常常会出现各种各样的错误.鉴于此,也可借助换元法解题,减少计算量,避免解题错误.
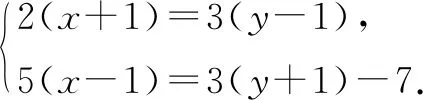
分析:如果按照传统的方法解方程组,学生就会面临着复杂的计算,进而在繁杂的计算中,出现各种各样的错误,严重制约了学生的解题效率.鉴于此,例2可借助单参数换元的方法,设2(x+1)=3(y-1)=6k,对其进行化简,得出x=3k-1,y=2k+1,并将其代入到第二个方程中,得到5(3k-2)=3(2k+2)-7,解出k=1.所以x=3k-1=2,y=2k+1=3.
例2借助了换元法,将原来方程中比较复杂的代数式,运用一个简单的字母进行代替,使得原本的方程变得简单.需要说明的是,在借助这一方法解方程组时,应按照“设元—换元—求新元—回代—求解—验根”的步骤进行,真正提升数学问题解决的效率[3].
2.3 运用换元法解决因式分解问题
在初中数学学习中,多项式的因式分解是考查的重点,也是学生学习的难点.学生在因式分解时,需明确因式分解和整式乘法的关系,并在新旧知识对比中,掌握因式分解的方法.在诸多的因式分解方法中,换元法尤为常用,并以其独特的优势,深受教师和学生的青睐.
例3分解因式(x2+3x+2)(x2+7x+12)-120.
分析:在解答这一问题时,如果按照常规的解题思路,先利用乘法公式展开再分解,问题就会变得非常困难,而直接运用换元法似乎也不太可能.此时,学生必须要认真分析题目的结构,将其初步变形,得到(x+1)(x+2)(x+3)(x+4)-120,之后对其重新组合,变形成为[(x+1)(x+4)][(x+2)(x+3)]-120,并化简为(x2+5x+4)(x2+5x+6)-120;之后,就可借助换元法,设x2+5x+4=y,则原式就等于y(y+2)-120=y2+2y-120=(y+12)(y-10),之后再代回原来的表达式,得(x2+5x+4+12)·(x2+5x+4-10),经过化简得出最终结果,即(x+6)(x-1)(x2+5x+16).
在例3的解答中,如何找到替换的“元”是关键.学生在解答该题之前,应对原式进行仔细观察和分析,将其适当变形,通过分解和重新组合,找到替换的“元”.之后,再借助换元法完成问题的解答.
2.4 运用换元法加强整式运算
在初中数学学习中,一些非标准型的整式运算相对比较复杂,学生在解决问题时,常常面临着无法下手、不知道如何解决的现象.鉴于此,可借助换元法,将整式中相同的部分视为一个整体,并借助新元进行代换,进而将复杂的整式运算转化为简单的数学问题.
例4计算:
(1-2-3-……-998)(2+3+4……+999)-(1-2-3-……-999)(2+3+4+……+998).
分析:在计算这一整式时,常规方法根本无法解决,唯有借助换元法的思想内涵,比如将(2+3+4+……+999)设为a,将(2+3+4+……+998)设为b,则原来的整式就可变为(1-b)a-(1-a)b,并据此进行求解.如此,通过换元法的应用,使得原本复杂的整式计算变得非常简单,真正提升了学生的解题效率[4].
综上所述,在初中数学解题中,学生常常会遇到非标准、非典型的问题,无法按照传统的方式进行解题,甚至在解题中频频出现错误.鉴于此,可基于换元法的特点,采用新“元”替换的方式,将原本复杂的数学问题简单化,以便于学生顺利解决这些问题.

