解决动态问题有方法——从平行四边形的动点问题出发

静宁县第三中学

赵芳宁

平行四边形中的动点问题是初中几何动态问题中的一类，在很多省市区中考压轴题的动态问题中是比较典型的代表[1].解决动态问题，可以从研究平行四边形的动点问题出发.这是本文中研究解决动点问题方法的基本思路.希望通过这样的研究，一方面对教师教学产生有利影响，另一方面对学生学习起到一定的促进作用.

1 平行四边形动点问题的解决思路

要想解决平行四边形中的动点问题，离不开平行四边形的性质和判定.纵观平行四边形的性质和判定，都与其边有莫大关系，所以解决思路主要集中于平行四边形的边.

由于动点问题中常会出现一个或两个甚至多个动点，因此随着这些点的不断运动，由点构成的图形形状和大小都会发生变化.故而，动点问题首先需要弄清楚点的运动情况，并且要学会用字母表示出线段的长度，或用字母表示出角的大小，然后利用平行四边形的性质建立方程并求解[2].

如此看来，平行四边形动点问题可通过以下四步解决：

(1)找两边相等.根据平行四边形的性质和判定，可知平行四边形的一组对边平行且相等.通常情况下平行是已知，因此只需找出相等的两边.

(2)写表达式.找出相等的两边后，结合动点的运动情况，写出这两边的表达式.

(3)分类讨论.一个点的运动情况比较简单，但两个或多个点的运动情况比较复杂，所以需进行分类讨论，且每种情况都应画出相应的图形.

(4)列方程求解.分类讨论后，根据线段相等列出方程并求解.当然，列出的方程一定要符合题意，对于不符题意的值则需舍弃.

2 例题解析

上述内容谈到，解决平行四边形动点问题的思路一共分为四步.为了让这一思路得以更直观地体现，从而帮助学生理解和掌握，现结合相关例题进行分析和说明.

图1

例1如图1，在四边形ABCD中，AD∥BC且AD=9cm，BC=6cm，点P，Q分别从点A，C同时出发，点P以1cm/s的速度由A向D运动，点Q以2cm/s的速度由C向B运动，当其中一点到达终点时，另一点也随之停止运动.问多长时间后线段PQ将四边形ABCD截出一个平行四边形？

分析：根据平行四边形动点问题的解决思路，可作如下处理.

(1)找两边相等.由于讨论的是平行四边形，所以根据其性质找出相等线段.

(2)写代数式.根据P，Q两点的运动情况，设时间为ts后，用含t的代数式分别表示线段AP,BQ,PD,CQ的长.

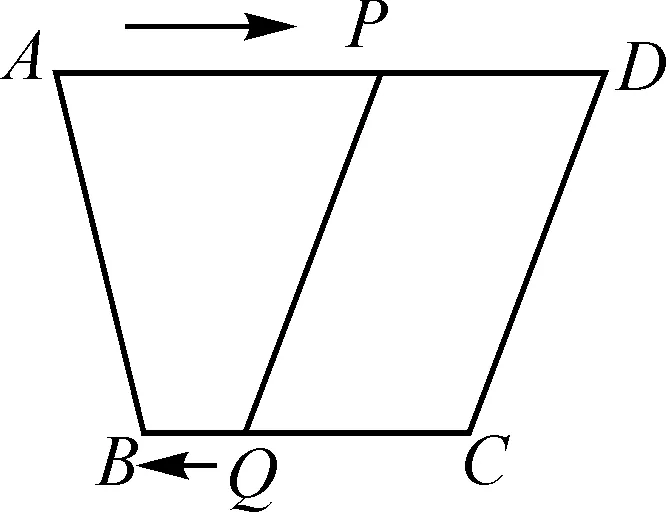
图2

(3)分类讨论.根据点的运动可分为两种情况，即AP=BQ(如图1),PD=CQ(如图2).

(4)列方程求解.分类讨论后，每种情况列出相应的方程并求解.

解：设ts后线段PQ将四边形ABCD截出一个平行四边形.

依题意可知，AP=t，BQ=6-2t，PD=9-t，CQ=2t.

①当AP=BQ时，t=6-2t,解得t=2.

②当PD=CQ时，9-t=2t,解得t=3.

综上所述，2s或3s后线段PQ将四边形ABCD截出一个平行四边形.

图3

例2如图3，点F在ABCD的边AD上，连接BD,BF，已知AF=8cm，BF=12cm，∠FBD=∠CBD，E是BC的中点.若点P以1cm/s的速度从点A出发，沿AD向点F运动，点Q同时以2cm/s的速度从点C出发，沿CB向点B运动，点P运动到点F时停止运动，点Q也同时停止运动.当点P运动多久时，以点P，Q，E，F为顶点的四边形是平行四边形？

分析：根据平行四边形动点问题的解决思路，可从以下四步进行分析.

(1)找两边相等.平行四边形ABCD中AD和BC互相平行，那么只需找出相等线段，即可判断出以点P，Q，E，F为顶点的四边形是平行四边形.

(2)写代数式.根据P，Q两点的运动情况，设时间为ts后，用含t的代数式分别表示AP,PF,CQ,EQ的长.

(3)分类讨论.根据点的运动分为两种情况，如图4、图5所示.

图4

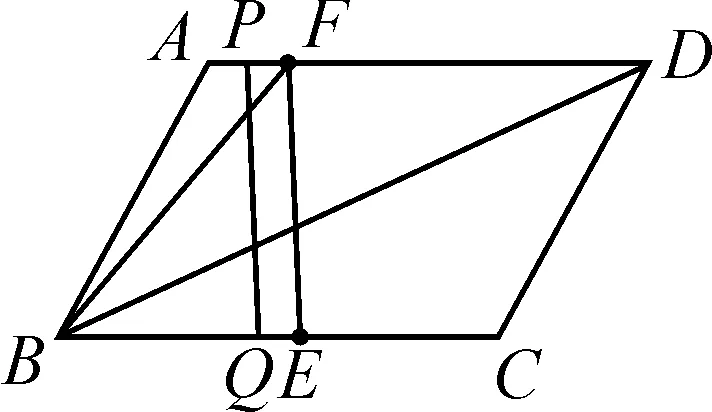
图5

(4)列方程求解.分类讨论后，对每种情况画出相应的图形并列方程求解.

解：设ts后线段PQ将四边形ABCD截出一个平行四边形.

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC.

∴∠ADB=∠CBD.

又∵∠FBD=∠CBD，

∴∠FBD=∠ADB.

∴BF=DF.

∵AF=8cm，BF=12cm，

∴AD=BC=20cm,DF=BF=8cm.

∵E是BC的中点，

∴BE=EC=10cm.

∵以点P，Q，E，F为顶点的四边形是平行四边形，

∴PF=EQ.

设当点P运动ts时满足条件，根据题意分析有如下两种情况.

①如图4所示，PF=EQ，即8-t=10-2t，解得t=2，即当点P运动2s时，以点P，Q，E，F为顶点的四边形是平行四边形.

②如图5所示，PF=QE，即8-t=2t-10，解得t=6，即当点P运动6s时，以点P，Q，E，F为顶点的四边形是平行四边形.

综上所述，当点P运动2s秒或6s时，以点P,Q,E,F为顶点的四边形是平行四边形.

3 解决动点问题的注意要点

动点问题的类型有很多，虽然动点所处的几何图形不同，但解决这样的问题都遵循四个步骤，上面通过两道例题已经做出了较详细的说明.在解决动点问题时需注意以下几个要点.

首先，熟练掌握分类讨论思想，学会如何分类讨论.以上两道例题的动点运动状态虽不一样，但都存在一定的规律，学生在分析过程中只需深入挖掘这一规律，并在此基础上用含字母的式子表示出相应的线段.需说明的是，分类讨论时一定要根据情况画出相应的图形以帮助学生理解问题[3].如上述两个例题中，都画出了相应情况的图形，使得动点的运动状态非常直观，更有利于学生分析问题.

其次，牢固掌握相关图形的性质和判定及计算方法.包括平行四边形动点问题在内，所有的动态问题都需要掌握两个方面的内容，一方面是相关图形的性质和判定，另一方面是方程等的计算.学生只有掌握这些基础内容，才能更高效地解决初中几何中的动态问题[4].

综上所述，要想解决动态问题，不仅要牢固掌握基础知识，还应熟练运用一些解题思想与方法.所以，对初中生而言，只有不断强化知识和提升学习品质，才能为日后的数学能力提升奠定基础.