钻研解法预设铺垫，对话追问引导回顾——一道“新定义”考题的教学设计与思考

江苏省南通市第一初级中学

周红娟

近年来，随着不少地区中考卷设计了一些“新定义”考题，使得相关地区不只在九年级的模拟试卷中出现大量“新定义”考题，在七、八年级的期末考试中也出现了很多“新定义”考题．而不少学生对这些推陈出新的“新定义”考题常感束手无策，“新定义”也使得一些学生在解题时增加了畏难情绪．笔者近期围绕一道新定义考题进行改编、再加工，设计了一节关于新定义考题的“一题一课”专题教学，带领更多学生挑战“新定义”考题，增强他们的解题自信，取得了较好的教学效果．本文结合这节课的教学设计，并围绕新定义考题的解题教学，提出一些思考，提供研讨．

1 一道“新定义”综合题的教学设计

1.1 考题呈现

在平面直角坐标系中，对于点M(a，b)，N(c，d)，作点M关于直线x=c的对称点M′，当d≥0时，将点M′向上平移d个单位，当d<0时，将点M′向下平移|d|个单位，得到点P，我们称点P为点M关于点N的对称平移点．

已知点B(m，m)，点A(1.5m，0)．点C为点A关于点B的对称平移点，当以A，B，C，O为顶点的四边形围成的面积为6时，求点B的坐标．

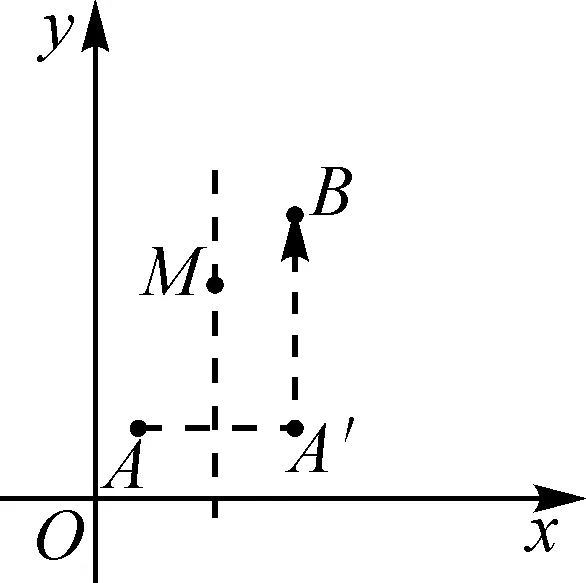
图1

1.2 教学环节一：读懂“新定义”，举例理解

问题1(出示“新定义”的题干后)若点A(1，2)，M(3，5)，对照“新定义”，分析点A关于点M的对称平移点的坐标．

教学预设：如图1，画出草图，先求出点A关于直线x=3的对称点A′(5，2)，再将点A′向上平移5个单位得B(5，7)．如果有学生感觉比较困难，可再提供一个变式——若C(3，1)，求点C关于点M的对称平移点的坐标．

1.3 教学环节二：运用“新定义”，拾级而上

问题2(在学生初步熟悉“新定义”之后，出示并研究考题)已知点B(m，m)，点A(1.5m，0)．点C为点A关于点B的对称平移点，当以A，B，C，O为顶点的四边形的面积为6时，求点B的坐标．

教学预设：先安排学生分析点A，B，C的可能位置，由于字母m的取值范围没有限定为正数，还要讨论m>0和m<0两种可能的情形．引导学生构造分析.

图2

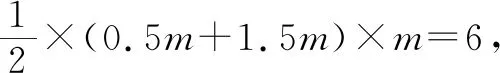
1.4 教学环节三：运用“新定义”，挑战难题

问题3已知点B(m，m)，点A(1.5m，0)，且m>0．点A向右平移1个单位得到点D，点A向右平移6个单位得到点G，以AD为边向上作正方形ADEF，以DG为边向上作正方形DGMN，点P为正方形ADEF的边上的一个动点，在点P运动过程中，若点B关于点P的所有对称平移点都在正方形DGMN的内部或边上，分析m可取的最值(最大值和最小值)．

图3

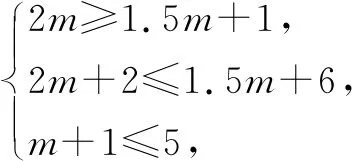
1.5 教学环节四：解后回顾，反思提升

小结问题1本课研究的这道新定义考题，首先是理解新定义，其中画图分析非常关键.你觉得怎样才能画出比较准确的图形？将你的经验与同学们分享一下．

小结问题3“问题3”中“虚线正方形”是如何生成的？在分析“虚线正方形”的四个顶点坐标时，你觉得怎样更快？请说说你的理解．

2 关于新定义考题解题教学的一些思考

2.1 深入钻研新定义考题的解法是备课前提

作为一份试卷中的新定义考题，在呈现时往往力求简洁，这样就不会像平时我们在新授课时那样，对一个新概念要从不同的角度进行定义或解释.比如，为了说清绝对值的概念，我们会基于数轴直观地给出定义，然后再给出绝对值的符号表示，最后举例让学生理解和运用．而考卷上的新定义，往往只是“单一”给出定义，教师在钻研这些新定义时，要善于给出新定义的“不同表征”(比如文字表述、符号表达、图形直观等)．在此基础上，再研究问题的解法．值得指出的是，不少新定义考题的第(1)问，往往直接代入计算就能获得结果，可是由于没有从图形的直观角度对第(1)问进行“再认识”，对于后续较难问题的求解是不利的.如果能在解题的起步阶段就对新定义有全方位、多角度、深层次的理解和揭示，特别是几何结构的揭示与理解，对后续较难问题的思路获取会有很大帮助．对于教师的课前备课，深入钻研新定义考题的解法，深刻理解新定义的几何结构是备课的前提和关键．

2.2 围绕较难题预设铺垫式问题是教学关键

在深刻理解新定义之后，对设问中的较难题要想清有哪些关键步骤，接着针对这些关键步骤预设铺垫式问题.铺垫式问题常常体现了“例值引路”“以退为进”等解题策略．具体来说，为了解决某个较难题，可能会先举一个让学生容易理解的例子，然后再拾级而上，给出一个相对有难度的“台阶”问题[1]，在这些铺垫问题的热身练习之后，学生再迎难而上，挑战难题，思路自然而然就生成了，这样不但实现了问题解决，而且帮助学生收获了解题自信．需要指出的是，课前预设的铺垫式问题应该更加“细致和密集”(可将“学情”想象得更弱作为预设铺垫问题或启发式问题的起点)，然而在具体教学实施时，要根据学情的实际情况出示铺垫式问题．比如，教学进程中，当有少数优秀学生已“跳过”课前预设的好几个铺垫式问题时，教师为了帮助更多还没跟上解题进度的学生，可以“打断”学生的讲解，请该学生讲讲他“跳过”的一些关键步骤，展开思维过程，让更多的学生跟上解题进度．这样，课前预设的有些铺垫式问题就不必出示了，因为已有学生帮助提供了这些铺垫式问题的讲解．

2.3 新定义考题讲评之后要安排回顾与反思

新定义考题一般都是在每份试卷中的最后一题(也称“压轴题”)，这类考题的最后一问往往综合性较强，成功解题需要打通多个关键步骤．这就要求教师在讲评这类较难题时，要充分预设解后回顾与反思的环节．如上文教学设计中所见，精心预设“小结问题”，组织和引导学生学会从不同角度进行回顾反思，才能促进深入反思、有效提炼，积累解题策略，感悟解题经验[2]．在预设“小结问题”时，要防范“大而空”的问题，比如“这节课学到了什么”“这节课感悟了什么思想方法”“你还有哪些疑惑”之类．预设出针对性强的小结问题，才能促进学生对解题过程中的关键步骤、易错点、表达细节等达到更好的回顾、反思与提升．