初中数学实践作业设计的探索与解读

高振卿 杨丽丽

[摘  要] 以鲁教版“勾股定理”为例，对初中数学实践作业（写作作业、探究作业、项目作业等）进行设计，并从学科素养点、作业设计说明、评价标准进行分析和解读，指出初中数学实践作业作为基础类作业的有益补充，在设计时应该满足以下要求：师生新时代发展的要求，学生个性化发展的要求，教师多元化评价的要求.

[关键词] 初中数学;实践作业;写作作业;探究作业;项目作业

基金项目：山东省首批基础教育教研基地（学科类：初中数学）——“初中数学作业设计的研究与实践”，2022年东营市市级教学成果培育项目——“反思性作业改革的探索与实践”，以及2021年度东营市教育科学“十四五”规划课题“生态圈·反思链：‘双减背景下初中学校‘反思性作业的校本探索与实践”（145JGYB21002）和 “基于‘精思文化引领的初中数学青年教师专业成长路径研究与实践”（145JGZX21008）.

作者简介：高振卿（1987—），硕士研究生，一级教师，从事课堂教学工作，曾获东营市青年骨干教师等荣誉称号.

引言

文[1]指出数学作业可以分为基础类、综合类、实践类、探究类等四类作业，并对每类作业进行了系统分析和解读，笔者读后受益匪浅. 借此机会，笔者以鲁教版“勾股定理”一章为例进行了实践作业的设计，取得了很好的效果，下面进行简单介绍，不当之处，敬请指正.

勾股定理，西方称为毕达哥拉斯定理，是最伟大的数学发现之一，在我国有着悠久的历史. 由于鲁教版教材在编写过程中遵循了螺旋式上升、简约性的原则，在学习勾股定理知识的过程中，只是探究它的内容和应用，对它的产生、发展的过程，多样的验证方法，以及它在人类文化发展史上的贡献没有做详细的介绍. 为了让勾股定理完整地呈现给学生，当学生完成了“勾股定理”这章的学习后，笔者在整章作业设计的基础上，额外增加了三个综合性实践作业，分别是写作作业——勾股定理的渊源、探究作业——“拼图法”验证勾股定理、项目作业——测量旗杆高度，这些作业都属于《义务教育数学课程标准（2022年版）》中的“综合与实践”领域的内容. 让学生更全面地认识勾股定理，是对课本知识的补充和拓展，通过教师的指导、同伴的合作交流和学生亲自动手操作验證等一系列数学活动，以数学小论文、活动操作、方案设计等方式把理论知识和实践应用结合起来;让学生完成勾股定理的探究历程，体会数形结合思想，体会勾股定理的数学价值和人文价值;开拓学生的视野，激发学生的创新意识和应用意识，激发学生学习数学的兴趣.

作业展示和解读

1. 写作作业——勾股定理的渊源

（1）作业要求.

关于勾股定理的记载最早见于公元前11世纪，直至今日仍是很多数学家和数学爱好者研究与探索的对象，请借助互联网，或去图书馆查阅相关资料，以《勾股定理的渊源》为题，写一篇数学小论文. 具体要求：主要以介绍勾股定理的发展过程为主线，从自己理解的一个角度出发介绍一下你对勾股定理的理解，字数400左右;论证角度要有新意，辅助材料要可靠，论述过程规范合理，论文结构明晰流畅. 完成后发至78162637@qq.com，下节课当堂交流展示，择优推荐发表.

使用时间：“探索勾股定理（1）”之前.

完成时长：1天 .

展示时间：“探索勾股定理（1）”的课前10分钟.

（2）学科素养点.

以数学小论文的形式考查学生的数学语言表达能力和创新意识. 通过写作的方式让学生了解中国古代数学史，感受中国数学魅力，培养他们的民族自豪感.

（3）作业设计说明.

通过这种“跨学科”形式的“数学小论文”，把数学知识以作文的形式书写出来，改变了传统的数学学习方式. 一是为提高学生的数学学习兴趣，锻炼学生用数学的眼光观察身边的事物和用数学的语言表达自己想法的能力. 学生通过数学小论文的书写，可以更好地体会如何从生活中获取数学知识，寻求解决问题的途径，增强学习自信心. 二是通过这种方式让教师了解学生数学学习的过程，对学生的了解更多元化，有利于教师进一步指导学生的个性化发展.

（4）评价标准.

A级：切合题意、数文结合、语言精练、结构完整;

B级：切合题意、图文并茂、语言精练、结构完整;

C级：切合题意、结构完整、语言不精、条理不清.

2. 探究作业——“拼图法”验证勾股定理

（1）作业要求.

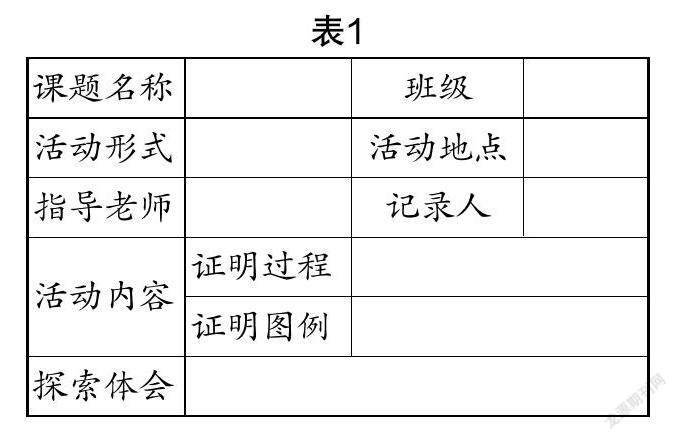
对勾股定理的验证方法有很多，大部分的方法可以归纳为“拼图法”，请先借助网络，或去图书馆查阅相关资料获得1～2种证明方法，然后通过小组交流和班内展示获得更多方法，感受不同方法之间的区别与联系，并独立完成下列表格（表1）.

活动准备：剪刀、直尺、三角板、双面胶、铅笔、厚纸板.

使用时间：“探索勾股定理（2）”之后.

完成时长：1天.

展示时间：1课时，安排于“探索勾股定理（2）”之后.

（2）学科素养点.

通过拼图验证活动，考查学生的数学核心素养、几何直观、模型观念、应用意识和创新意识. 以学生的个性化方案验证勾股定理，一方面展示学生的思维，另一方面让学生体会到什么是数形结合.

（3）作业设计说明.

由于教材编写设计的特点，课本知识只是呈现了简约的勾股定理的基本知识和应用，对于其他方面知识的介绍很少，特别是定理的证明过程只是简单呈现了一种证明方法，对于其他有趣的证明方法没有进一步讲解，这满足不了学生个性化发展的需求，也激发不了学生的学习兴趣，所以在学生完成“探索勾股定理（2）”的学习任务后，教师设置了以“‘拼图法验证勾股定理”为主题的自主实践作业，它属于《义务教育数学课程标准（2022年版）》中的“综合与实践”领域的内容. 学生通过方案设计、剪纸、拼接、验证等一系列数学活动进一步了解勾股定理，能拓宽思维和视野，培养创新意识，激发数学学习兴趣.

（4）评价标准.

A级：准备充分、拼圖完美、过程完整、讲解清晰;

B级：准备充分、拼图有效、过程完整、讲解明了;

C级：准备不全、拼图有效、过程一般、讲解不明.

3. 项目作业——测量旗杆的高度

（1）作业要求.

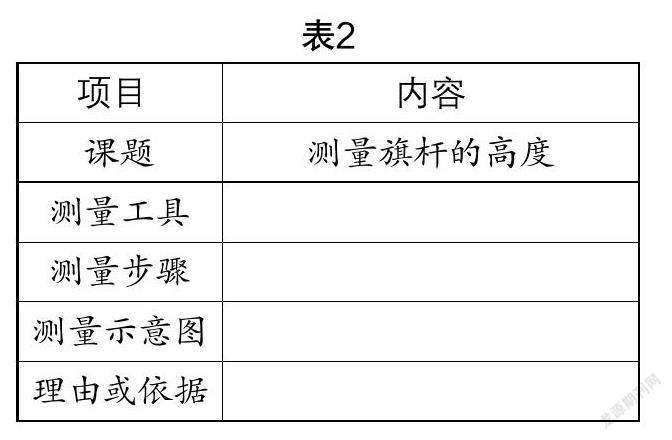
你想知道学校旗杆的高度吗？在不放倒旗杆的前提下，你有办法测量吗？如果有兴趣请以小组为单位完成设计方案，并给出具体的解决方法和测量工具. 尽可能提供多种方法（使用不同的数学知识），并填写下列表格（表2）.

活动准备：钢卷尺、电子尺、经纬仪、铅笔、笔记本、计算器等.

使用时间：本章学习过程中.

完成时长：2天（此作业贯穿本章学习的前后）.

展示时间：1课时，安排于本章章末复习课的小组展示.

（2）学科素养点.

通过完成项目作业，考查学生的抽象能力、运算能力、模型观念、应用意识和创新意识. 让学生体验问题解决方法的多样性，培养学生的合作交流意识和探索精神. 学生通过动手实践，体验研究过程，学习研究方法.

（3）作业设计说明.

该项目作业考查学生对勾股定理的实际应用情况，先以小组合作的形式给出设计方案和依据（如构造直角三角形），再根据设计方案利用仪器进行实地测量，给出能够直接使用的数据，利用勾股定理计算出旗杆的高度. 这是将实际问题转化为数学问题的活动，这种建模思想是学生在初中数学学习过程中必须掌握的数学思想之一. 这个项目作业的设计，既考查学生知识运用、动手操作和运算的能力，又考查学生的团队协作精神和小组合作意识. 在这个项目作业完成过程中，能让学生体会用数学的眼光和数学的思维来发现和解决问题. 学生通过参与数学探究活动，形成好奇心与想象力，发展创新意识与科学价值观. 当然，学生也可以通过参与学科间的综合实践活动与项目学习，形成应用意识和创新能力. 学会数学学习，可以为学生终身学习打下基础.

（4）评价标准.

A级：准备充分、操作准确、过程完整、讲解清晰;

B级：准备充分、操作有效、过程完整、讲解明了;

C级：准备不全、操作有效、过程一般、讲解不明.

几点思考

1. 符合时代发展的要求

新时代的课程发展要求学生除了掌握基础知识外，更多的是体现学习能力. 《义务教育数学课程标准（2022年版）》中提出：课程内容的呈现方式要注重数学知识与方法的层次性和多样性，适当考虑跨学科主题学习和综合性项目式学习（详见文[2]）. 在本案例中，在学生完成勾股定理基础性作业的基础上，笔者结合学情，适当开展了主题式、探究式、项目式实践作业的探索，目的在于让学生学会知识、应用知识、锻炼能力，在实践中落实学生的数学核心素养.

2. 符合学生个性化发展

传统作业除了通过分层探索外，没有结合学生自身意愿和想法把知识应用到实践中，降低了学生的学习积极性，而且在学生的主动性学习方面的引导也不够. 笔者在整章作业设计的基础上，增加了写作作业——勾股定理的渊源，目的在于让学生通过自学的方式深入了解勾股定理，通过上网查阅、图书馆资源查询等方式进行自主学习，随后以小论文的方式呈现研究成果;探究作业——“拼图法”验证勾股定理，目的是让学生通过动手操作的方式验证自己的想法，通过探索不同的拼图方式，感受数学的魅力;项目作业——测量旗杆的高度，让学生通过小组合作的形式自主设计方案，寻找合适的工具，现场操作、收集数据，在体现出学生合作精神的同时，表现了学生的智慧. 以上三种方式的实践作业，旨在激发学生的学习自主性和主动性，将书本的理论知识应用到生活中去，体现数学的价值.

3. 符合教师多元化评价

现在对学生的评价主要体现在结果上，比如分数、等级，这样的评价单一且忽略了学生在学习过程中的表现. 以上三种实践作业，笔者在结果评价的基础上，更多体现过程评价，并给出了每个活动的评价标准，比如项目作业评价分为三个层次，A级：准备充分、操作准确、过程完整、讲解清晰;B级：准备充分、操作有效、过程完整、讲解明了;C级：准备不全、操作有效、过程一般、讲解不明. 这样的分层式评价更多重视学生的学习过程，从不同层面上让教师了解学生，客观合理地评价学生、肯定学生，激发学生的学习积极性，提高学生的探索精神.

参考文献：

[1]喻平. 核心素养指向的数学作业设计[J].数学通报，2022（05）：1-7+12.

[2]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.