数学教学要注意引导学生学会思维
王春瑜

【关键词】小学数学;学会思维;操作感知;建构模型;发现规律;提升素养;《图形的放大和缩小》
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2023)09-0080-04
南京大学郑毓信教授指出:数学教学必须超越具体知识和技能,深入到思维的层面,由具体的数学方法和策略过渡到一般性的思维策略与学生思维品质的提升,帮助学生通过数学学会思维,提升思维的综合性与灵活性、自觉性与创造性、严谨性与深刻性等。苏教版六下《图形的放大和缩小》一课的教学重点是引导学生认识图形的放大和缩小,能利用方格纸按一定的比把简单图形放大或缩小。这部分知识对学生来说难度并不大,那么,如何在教学中引导学生真正做到会学、活学、深学,从而有效促进他们学会思维呢?笔者通过实践与研究发现,关注学习起点、挖掘知识本原、设置认知冲突、经历探究过程是实现这一愿景的有效路径。
一、操作感知,初探奥秘
师:同学们,我们用word编辑文档时,常常要将插入的图片放大或缩小,谁来给大家演示一下?(学生操作)
师:点击图片后,图片边线上一共显示8个点,你为什么拖拉的是顶点?
生1:拖拉角上的顶点,长和宽会同时变大或变小,如果拖拉边上的中点,就只有长变化,或者只有宽变化。
生2:拖拉顶点,图片不变形,拖拉其他点,图片会变形。
师:像这样放大、缩小时形状不变的情况,就是我们今天要研究的“图形的放大和缩小”。要想图形不变形,只要拖拉角上的顶点就可以。顶点为什么这么神奇呢?秘密就藏在图片工具里。(出示“锁定纵横比”)你知道“锁定纵横比”是什么意思吗?
生:纵是宽,横是长,锁定纵横比就是宽和长的比不变。
师:是呀,放大或缩小图片时,使图片不变形的秘密就是“锁定纵横比”。
课始,教师将数学知识与信息技术有机整合,鲜活的素材、巧妙的方式有效激发了学生的好奇心,进而揭示放大或缩小图片且使其不变形的奥秘是“锁定纵横比”,并以此为起点,从定性认识过渡到定量刻画,为用“比”的方式描述图形的放大和缩小做好准备。
二、追本溯源,建构模型
1.尝试放大
师(出示一个长6、宽4的长方形):这个长方形的纵横比是多少?那长和宽怎样变化才能锁定2∶3这个纵横比呢?在方格纸上尝试画出长方形放大或缩小后的样子。
生1:我画了一个长12、宽8的长方形,长和宽都扩大了2倍。
生2:我把长和宽都扩大3倍,画了一个长18、宽12的长方形。
生3:我把长和宽都缩小2倍,画了一个长3、宽2的长方形。
生4:我把长和宽都扩大1.5倍,画了一个长9、宽6的长方形。
师:观察这些放大或缩小的长方形,你有什么发现?
生:纵横比都是2∶3,形状相同。
师:如果方格纸足够大,你能画多少个这样的长方形?
生:只要锁定纵横比,我们就可以画出无数个大小不同、形状相同的长方形。
在揭示图形的放大或缩小的意义之前,紧扣“纵横比不变”,放手让学生直接画出长方形放大和缩小后的图形。学生在操作实践、展示交流中积累了活动经验,锻炼了综合思维,初步感悟到图形放大和缩小的本质属性:大小改变,形状不变。
2.描述放大
(1)由形想比
师:老师从大家画的长方形中选择一个放大的长方形,这个长方形是把每条边放大到原来的2倍得到的,仔细观察原来的长方形与放大后的长方形,你能用一个比表示这个变化过程吗?比的前项表示什么?后项呢?
生1:我想用2∶1表示,2表示放大后的长,1表示原来的长;2也表示放大后的宽,1也表示原来的宽。
生2:我也是用2∶1表示的,但2表示放大后的周长,1表示原来的周长。
生3:我用1∶2表示,1表示原来的宽,2表示放大后的宽。
生4:我用4∶1表示,4表示放大后的面积,1表示原来的面积。
生5:我用1∶4表示,1表示原来的面积,4表示放大后的面积。
(2)以比定形
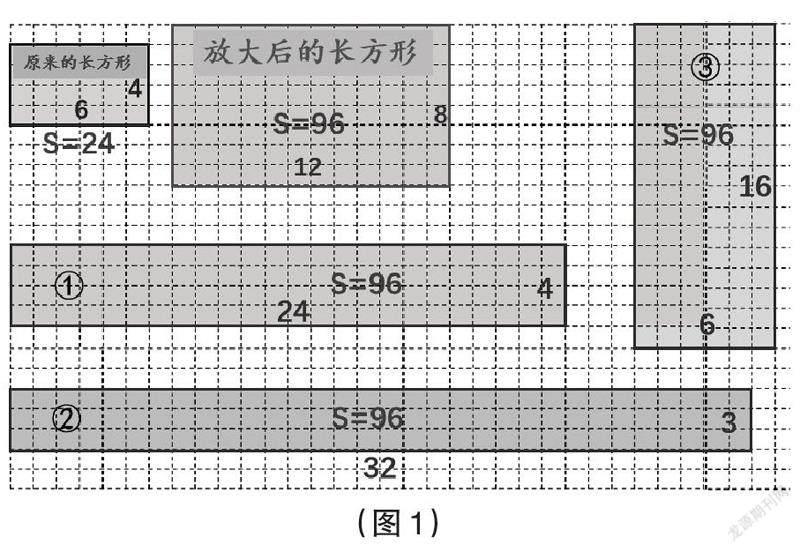
师:同学们想到了用对应边长度的比、周长的比、面积的比来表示图形的变化,都有自己的道理,这些比都能说清楚长方形的这种变化吗?我们先来讨论面积比1∶4。(出示图1)。
师:①②③号长方形的面积都是原来长方形的4倍,原来的长方形与它们面积的比都是1∶4,这些长方形都是原来长方形放大后的图形吗?
生1:不对,①②③号长方形和原来相比,全都变形了,它们没能锁定纵横比。
生2:如果用面积比说明图形的放大,得到的图形有很多种情况,面积虽然都是原来的4倍,但形状可能会发生变化,所以用面积比来说明图形的放大不准确。
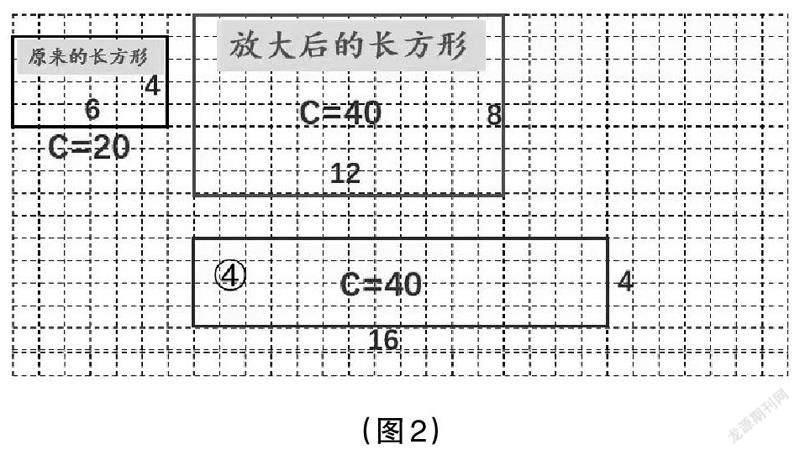
师:既然面积比不能准确描述图形的放大,那周长比呢?刚才的研究有给你一些启发吗?
生1:原来的周长是20,放大后的周长是40,周长是40的长方形也不止一个,不一定长是12、宽是8。
生2:這样看来,用周长比来说明长方形的放大也不准确,因为周长相等的长方形也有无数个,不一定就是我们要描述的长方形。
师(出示图2):是的,周长变成原来的2倍时,可能是长12、宽8的长方形,也可能是长16、宽4的长方形,当然还有其他可能,所以周长比也不能准确描述图形的放大。
师:最后我们来讨论边长,放大后的长和原来的长是一组对应的边长,放大后的宽和原来的宽也是一组对应的边长,对应边长的比能准确描述图形的放大吗?
生1:放大后长方形的长和原来长的比是2∶1,宽的比也是2∶1,长和宽都只有一种可能。
生2:放大后长方形的长是12、宽是8,长和宽固定了,长方形的大小和形状就固定了。
师:看来,用对应边长的比来描述图形的放大具有唯一性,锁定了对应边长的比,也就锁定了图形的大小和形状。
(3)揭示放大
师:放大和缩小都是与原来的图形相比较,在描述放大和缩小时,数学上规定把变化后的长度作为前项,把原来的长度作为后项,这里放大后的长方形与原来长方形对应边长的比是2∶1,也就是把原来的长方形按2∶1的比放大。
师(出示按3∶1的比放大的长方形):现在的长方形是怎样放大的?如果要把原来的长方形按4∶1的比放大,你打算怎么做呢?
用比来描述图形的放大,边长比、周长比、面积比,哪一种比更合理呢?教师从学生的学习起点出发,带领他们经历自主研究、讨论辨析、发现规律、建模应用的过程,从“由形想比”到“以比定形”,发现用对应边长的比描述图形放大最合理,在对比冲突中还原知识形成的本来面貌,培养其思维的深刻性和创造性。
3.认识缩小
师:把原来长方形的每条边都缩小到原来的二分之一,我们可以说是按几比几缩小呢?在小组内说一说。
师:观察这些表示放大和缩小的比,你能从中看出图形的变化吗?
生1:前项比后项大就表示放大,前项比后项小就表示缩小。
生2:比值就是他们放大或缩小的倍数,比值比1大就是把原来的图形放大,比值比1小就是把原来的图形缩小。
师:如果是1∶1呢?
生:原来的图形既不放大也不缩小。
师:我们之前学习的平移、旋转、画轴对称图形都是把原来的图形按1∶1的比变化,图形的形状、大小都不变。(课件分别演示)今天学的放大和缩小,你能看出其中的变与不变吗?
生:图形的大小变了,但形状不变。
在认识放大的基础上放手让学生说说缩小的含义,然后比较表示放大和缩小的比的特征,再用特殊比1∶1勾连“图形的运动”领域知识间的内在联系,升华了图形放大和缩小的本质属性,凸显了六年级数学在小学数学体系中的统领作用,有助于培养学生思维的综合性。
三、思维拓展,发现规律
师:学会了长方形的放大和缩小,你能按2∶1的比画出直角三角形放大后的图形吗?(学生操作)你是怎样画的?
生:把两条直角边分别放大到原来的2倍。
师:直角边放大到原来的2倍,斜边也放大到原来的2倍吗?可以怎样验证?
生:用尺量一量。
师:可以的,一起量一量。除了测量,还有其他验证方法吗?
生:原来的斜边可以看作4×2长方形的对角线,现在的斜边上可以找到两个4×2的长方形,所以斜边也放大到原来的2倍。(如图3)
师:直角三角形的每条边线都放大到原来的2倍,它内部的对应边会怎样变化?以斜边中点到直角顶点的连线为例,你发现了什么?(出示图4)
生1:这条连线也放大了2倍。
生2:三角形按2∶1的比放大,外面的边线放大到原来的2倍,内部的对应边也放大到原来的2倍。
师:图形在放大或缩小时,看得见的、看不见的对应边都在按同样的比放大或缩小。
图形放大或缩小时,是不是所有对应的邊长都同步变化呢?学生潜在的想法需要教师的设计才能呈现出来,教学直面学生的现实,既要面对能听到的、看到的想法,还要面对他们头脑中潜在的、尚未敞亮的想法。这里分两个层次研究了直角三角形的斜边和内部边线的放大情况,有测量,有推理,学生思维的深刻性、严谨性不断得到提升。
四、实践运用,提升素养
师:你能用今天所学的知识解决下面的问题吗?
如皋的文庙大成殿已有四百多年历史,是国内罕见的全楠木结构,坐落于如皋师范学校附属小学校园内。一群建筑爱好者打算制作一个大成殿模型。通过测量,大成殿主体建筑以及前面的回廊、月台的总占地大约是一个边长为30米的正方形。(1)在方格纸上画出大成殿缩小后的平面图。(每个小方格的边长表示1米)我是按( )∶( )的比缩小的。(2)大成殿的高约12米,根据你的比制作出的大成殿模型高约( )米。
学以致用,是数学学习的本意;通过数学学会思维,是数学教学的目标。课尾设置开放题,综合运用本节课所学的知识,自主确定合适的比画出缩小后的图形,有助于培养学生用数学眼光观察现实世界、用数学思维思考现实世界、用数学语言表达现实世界的意识和能力。
(作者单位:江苏省如皋市教师发展中心)

