视觉化呈现数学知识,培养学生结构化思维
吴丽娟 朱正林
【关键词】小学数学;结构化思维;视觉化呈现
【中图分类号】G623.2 【文献标志码】A 【文章编号】1005-6009(2023)09-0087-02
客观现实世界具有整体性、复杂性、统一性等特征,思维是人脑对客观现实的认知,也具有整体性和结构性。数学结构化思维,是指在数学学习活动中把数学问题作为思维的对象,展开结构化思考,从而建构数学问题的思维过程。知识视觉化呈现,是指从视觉层面帮助学生梳理知识结构,并使之进一步转化为学生的内在知识,从而实现学生的知识建构和思维发展目标。知识视觉化呈现能使抽象的数学知识变得可视化与形象化,从而促进学生把握数学活动本质,形成数学知识结构,培养数学结构化思维。本文主要探讨指向结构化思维培养的数学知识视觉化呈现策略。
1.巧用数形结合,探究知识本质
巧用数形结合,引导学生将几何图形、数量关系等有效结合起来探究问题,能使抽象的知识形象化、视觉化,便于学生具体而直观地分析问题,有利于他们理解与掌握知识本质。在教学中,教师应注意引导学生通过数形结合的方式分析和解决数学问题,带领他们在观察、分析的基礎上发现知识间的内在联系,理解知识的本质。
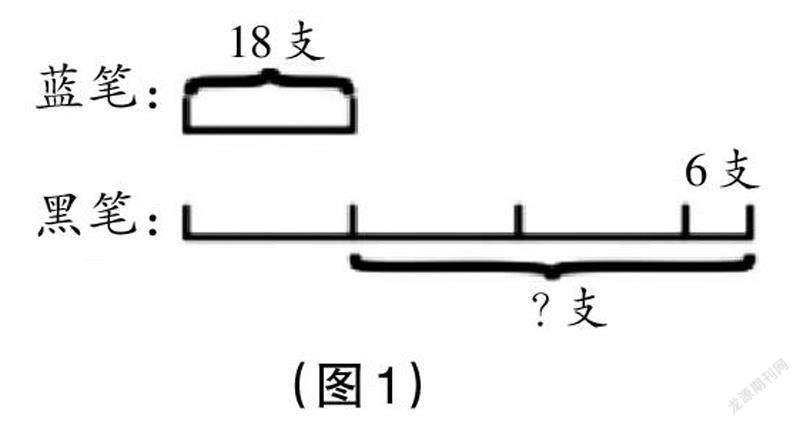
如教学“倍的认识”时,有不少类似于“蓝笔共有18支,黑笔是蓝笔的3倍,还多6支,黑笔比蓝笔多多少支?”的题目,考察的是学生运用倍数关系解决问题的能力,对他们来说不太容易理解。此时,教师可以引导学生画线段图,将题目中的文字描述转换为视觉化的线段(如图1),从而实现数量关系问题的简单化处理。
2.巧用类比迁移,实现信息关联
类比迁移是一种非常有效的问题解决方法。在数学教学中,教师应注重引导学生从结构关系层面进行类比迁移,从而使他们有效实现对新知识的理解与掌握。另外,还要注重引导学生发散思维,促进他们完善知识结构,培养结构化思维。
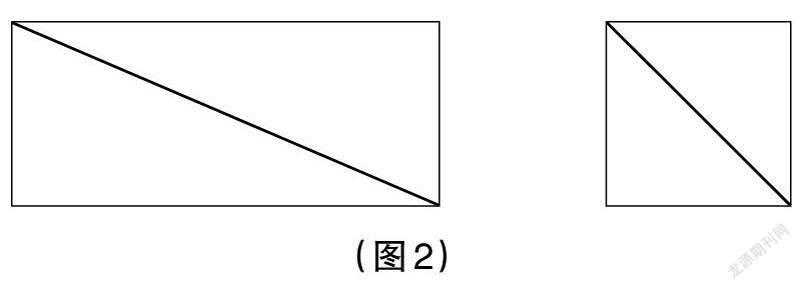
如教学“三角形的认识”时,教师就可以采用类比迁移的方法,引导学生在四边形的认知基础上理解三角形的特征。首先,教师可以在教学前引导学生回忆四边形的一些特征,如在黑板上画一个长方形与一个正方形,让学生说一说它们之间的异同,学生可能会发现:在相同点方面,正方形与长方形均有四条边、对边平行且相等、内角和均为360°、内角均为90°等;在不同点方面,长方形邻边长度不同,而正方形四条边等长,两者对称轴数量不同……然后,将上述正方形与长方形变成如图2所示的图形。这时学生可以根据长方形的特征得出,由长方形对角顶点分割成的两个三角形,有两个角是锐角且不相等,另一个角是直角,且三条边不相等;长方形内角和对分以后,两个三角形的内角和均为180°,如此学生便可由对长方形的认知推理得到直角三角形的特征。同理,根据正方形的特征可以得出,由正方形对角顶点分割成的两个三角形有两个锐角且均为45°,一个角是直角,且有两条边相等,内角和均为180°,此时学生便可由对正方形的认知推理得到等腰直角三角形的特征,并可用类似的方法来探究钝角三角形、锐角三角形的特征。这样学生理解起来更容易,且在类比迁移过程中实现了四边形知识与三角形知识的联结,有助于他们培养结构化思维。
3.巧用思维导图,形成知识结构
思维导图有助于学生对知识脉络与思维逻辑进行梳理和思考,从而更好地形成知识结构,完善认知结构。在小学数学教学中,教师要注意引导学生绘制与课堂知识内容、思维方式和学习方法相关的思维导图,促进他们形成分析与整理数学知识的能力。
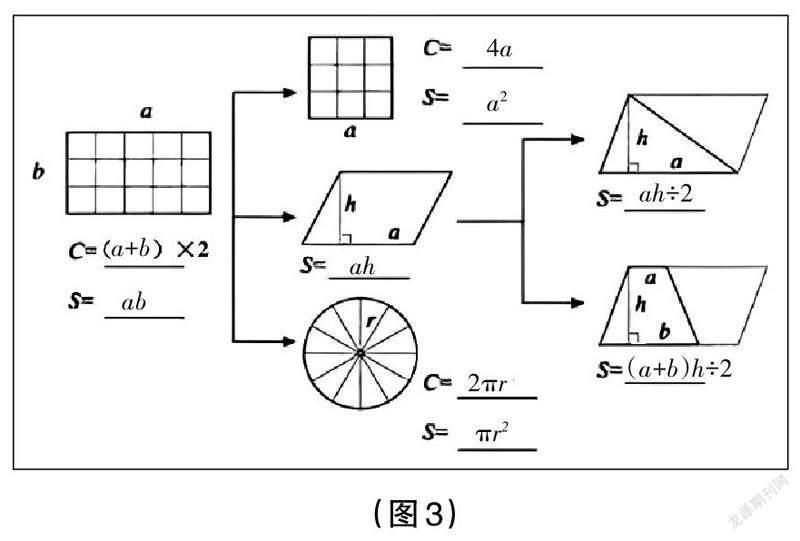
如教学“平面图形的周长和面积”时,教师可以让学生在预习时对有关平面图形周长与面积的知识进行梳理,并以思维导图的形式呈现出来。在课堂教学中,教师可以以如图3所示的思维导图为例引领学生展开学习,从而促进学生完善自己的思维导图,更好地明晰不同类型平面图形的周长与面积计算公式之间的关联。这样教学,有利于学生形成具有视觉化的知识结构以及清晰的知识脉络,从而逐渐形成结构化的思维方式。
综上所述,在小学数学教学中,教师要注意根据教学内容和学生的认知特点,视觉化呈现数学知识,引导学生梳理知识脉络,促进他们在大脑中构建系统的知识体系,帮助他们形成具有关联性、整体性、系统性的结构化思维,逐渐养成结构化思维的习惯,从而推动其核心素养的培养和提升。
(作者单位:江苏省淮安市人民小学)

