基于CDEM-MPM 耦合的软地面车辆侵入规律研究

程鹏达，冯 春，2*，常宁东，周 俊，朱心广

（1.中国科学院 力学研究所，北京 100190；2.中国科学院大学 工程科学学院，北京 100049）

1 引言

车辆通行性研究在军事、建筑业和农业等领域起着重要作用，尤其在军事方面，高机动性和可靠性已成为现代车辆设计和研究的重要目标。当场地环境复杂时，车辆通行性不仅与车辆本身有关，还与地面地形条件和地面土力学特性相关。因此，车辆-地形力学耦合动态特性的研究具有重要的应用价值和科学意义。

车辆车身（如轮胎、履带、板、腿、底座、叶片和尖齿）与土体、土壤嵌入障碍物（如植被根/茎、岩石）接触过程对车辆通行性有重要影响。近年来，美国陆军、北约成员国和伙伴国的军队持续提出车辆全地形通行性预测的需求［1-2］。当前，北约采用的车辆通行性评估主要侧重于车辆机动性，即车辆速度（NATO Reference Mobility Model，NRMM）模型［3］。NRMM 模型开发于20 世纪70 年代，并在80 年代和90 年代持续更新，该模型基于经验关系来预测给定地形上的车辆机动性，同时考虑地形力学等变量，如土壤圆锥指数（CI）［4］、USCS（ASTM 2000）土壤类型、土壤湿度、地表覆盖条件（正常、水或雪）和深度、土地利用（农业、灌木丛、森林、湿地、城市等）、坡度（上坡、下坡和侧坡）、表面粗糙度、土堆/沟渠障碍物尺寸和间距、树木/植被茎的大小和间距、可见度以及道路参数（道路类型、车道、桥梁、隧道等）。基于经验关系，NRMM 对20 世纪60 年代至80 年代的车辆适用性较好，但很难推广到当前多类型和尺寸的车辆，同时调整经验关系需要全尺寸车辆试验，非常昂贵且耗时。21 世纪初，北约提出需要更新、改进和重新验证软土-车辆耦合动力学模型。2016 年至2018 年，北约RTG-248 研究任务组提出分阶段更新方案，短期方案基于Bekker-Wong 理论［5-6］，该理论较Mohr-Coulomb 模型能更好地描述土壤剪切应力应变关系，也称之为简单地形力学模型。长期方案是基于离散元法（Discrete Element Method，DEM）或有限元（Finite Element Method，FEM）模型，也称之为复杂地形力学模型。基于Bekker-Wong 理论，国内外众多学者开展了大量研究［7-10］，针对不同类型车辆-土壤相互作用简化关系，推导了二维或三维条件下土壤特性、剪切速率、土壤推力、牵引力、阻力等参数间关系。基于复杂地形力学模型，能够更为真实地预测车辆车身（轮胎、履带、支腿、铲斗、叶片、尖齿等）上的三维反作用力，以及土壤三维变形和流动［1］，如车辙深度/宽度/形状、车辙侧壁高度和车辆前方的推土。与车辆耦合的复杂地形力学通常基于连续介质模型、连续-非连续模型、非连续模型，常用方法包括有限元法（FEM）［11-12］、连续-非连续单元法（Continuum-discontinuum Element Method，CDEM）、离散元法（DEM）、光滑粒子流体动力学（Smooth Particle Hydrodynamics，SPH）［13］和物质点法（Material Point Method，MPM）等。车辆-土壤耦合作用的物理现象十分复杂，通常借助数值方法，以较高的计算成本为代价得到更为详细的结果，且不依赖经验参数。值得注意的是粒子模型将土壤模拟为粒子集合，可以捕捉到土壤变形流动的复杂过程［11］，例如推土或土壤混合过程，而连续介质模型对该过程的描述存在一定困难。此外，针对土壤应力应变本构关系，Bekker 做出了开创性研究［5］，Wong 等在Bekker 本构关系基础上提出了Bekker-Wong 本构关系［6］。近年来，许多研究人员专注于更精确的半经验本构关系，多数情况下这些本构关系仍然受到Bekker 模型的启发［14］。

目前关于车辆-地形力学多介质耦合动力学仍是车辆装备通行性研究的核心问题，具有重要的应用价值和科学意义。因此，本文基于自主知识产权的连续-非连续单元法（CDEM）［15-16］和物质点法（MPM），数值模拟某型装备引起软土地面的变形及侵入软土的过程，定量研究车轮载重、软土弹性模量、软土强度参数与软土表面压应力、侵入深度等参数之间的关系，获得车轮侵入软土深度的变化规律，为复杂地形土壤环境下军事行动分析、任务规划和战争模拟预测的车辆通行性提供理论依据。

2 数值方法

2.1 连续-非连续单元法（CDEM）

基于拉格朗日方程的连续-非连续单元法（CDEM）是一种有限元与离散元耦合的显式数值分析方法，主要用于材料渐进破坏过程的模拟。CDEM 的计算域通常包含连续块体和分散块体，分别作为有限元（FEM）和离散元（DEM）方法的计算域［15-16］，如图1 所示。

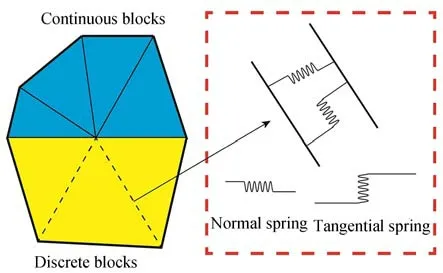
图1 CDEM 计算域Fig.1 Computational domain in the CDEM

CDEM 基于增量方式的显式欧拉前差法求解动力问题，主要包含节点合力计算及节点运动计算两个部分。节点合力如下：

其中：F为节点合力，FE为节点外力，Fe为节点变形力（由单元应力贡献），Fc为接触界面贡献的节点力，Fd为节点阻尼力。

节点运动计算如下：

其中：a为节点加速度，v为节点速度，u为节点位移全量，m为节点质量，Δt为计算时步。

CDEM 中，连续求解域的有限元单元应力及节点变形力采用增量法计算：

其中：Bi，Δεi，Δσi，wi和Ji分别为高斯点i的应变矩阵，增量应变向量，增量应力向量，积分系数及雅克比行列式；n和n-1 为高斯点i当前时刻及上一时刻；D，Δue，Fe分别表示单元的弹性矩阵，节点增量位移及节点力；N表示高斯点个数。

CDEM 中，将非连续求解域划分为不同于原始连续块体的分散块体，这些分散块体之间的相互作用可以转化为虚拟弹簧接触力。本文采用半弹簧-半棱联合接触模型快速标记接触对，并计算接触力［15-18］。

局部坐标系下，块体间的接触力可以表达为：

其中：F，K和Δu分别为虚拟弹簧力的增量，刚度和相对位移；下标nt 和s 分别代表法向和切向。

基于不同介质的物理力学特性，当虚拟弹簧达到给定的失效准则时，块体间连续界面将转化为不连续的断裂面，用于表征材料的断裂、滑移、碰撞等非连续特征。本文选择最大拉应力准则为失效准则，剪切强度选择Bekker 模型描述，对于准静态问题，该模型可以简化为Mohr-Coulomb 模型。

2.2 物质点法（MPM）

物质点法（MPM）是由Sulsky 等人提出的一种无网格的方法［19］。MPM 方法将连续体离散成一组质点，质点携带了所有物质信息，其运动代表物质的变形，避免了界面描述等问题。质点和背景网格固连后，物质点信息映射到背景网格点，动量方程在背景网格上求解，得到网格点加速度、速度和位移。将网格点运动量映射回物质点，得到物质点的运动信息。丢弃变形后的背景网格，重新构造背景网格，进而避免了网格畸变。MPM 方法结合Lagrange 方法和Euler 方法的优点，适用于冲击、碰撞、破坏、加工成型等大变形问题，但是反复映射带来较大的计算量，并容易产生误差。

MPM 方法动量方程的弱形式为［20］：

其中：δui、ρ、¨、σij、fi和ti分别为虚位移、密度、加速度、Cauchy 应力、体力和边界牵引力，V表示材料域，Γ表示材料边界。

离散颗粒的质量密度可以表示为：

其中：Mp为质量，np为颗粒总数，δ为狄拉克函数（Dirac Delta Function），xpi为颗粒p的坐标。

将质量密度代入动量方程的弱形式，得到：

其中，h-1是满足体积积分所需的边界层假设厚度［21］。

MPM 方法的求解过程中，质点和背景网格固连。每个时间步计算结束后，更新粒子的速度和位置，并为下一个时间步定义新的规则网格。因此，与有限元法相比，避免了网格畸变。通常情况下，所有时间步中都可以使用相同的固定规则网格。因此，可以通过背景网格中节点的有限元形函数，实现粒子和节点之间的映射：

其中：uip、uiI、uip，j分别为颗粒位移、网格位移和颗粒位移的导数。g为有限元的网格节点总数，对于一个六面体单元，g=8。

2.3 CDEM-MPM 耦合计算方法

本文选择CDEM-MPM 耦合方法计算车轮和软土地面相互作用的过程，以精确模拟软土地面变形、损伤和破坏过程中涉及的多种物理现象。通过引入颗粒-表面/边缘接触算法，实现MPM 计算域和CDEM 计算域相互作用，该接触模型耦合分析如图2 所示［22］。

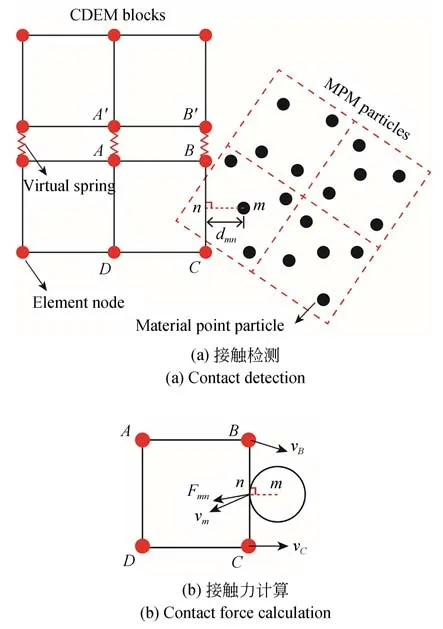
图2 CDEM-MPM 耦合分析示意图Fig.2 Schematics of CDEM-MPM coupled analysis

如图2（a）所示，通过满足以下要求建立接触：

其中，d和R分别表示距离和颗粒半径。

当CDEM 单元与MPM 物质点接触时，如图2（b）所示，法向接触力和剪切接触力计算分别如下：

其中：k为接触刚度，n为单元边界方向，vm为颗粒的速度矢量，vn为单元边界上颗粒m投影点的速度：

其中：vB和vC为节点速度。

因此，可以通过颗粒-表面/边缘接触法实现CDEM-MPM 的耦合。在每个时间步中，首先检测MPM 计算域和CDEM 计算域是否接触，若接触，则计算它们间的接触力，实现相互作用；若未接触，则它们会独立更新，以获取节点变量的信息。为了在数值计算中获得稳定的解，背景单元应至少包含一个颗粒，即颗粒半径不超过背景网格单元长度的一半。

CDEM-MPM 耦合方法在解决大变形问题上具有突出优势，同时也大幅降低了计算成本。近年来，相关研究也验证了通过颗粒-表面/边缘接触法算法实现块体和粒子耦合（CDEMMPM）算法的准确性［23-24］。

3 车轮-软土耦合动力学数值模拟

本文采用连续-非连续（CDEM）方法对车轮进行建模，采用物质点法（MPM）对软土进行建模。最后，通过数值模拟分析车轮-软土地面的相互作用，并讨论车轮侵入深度的变化规律。在国际地面车辆系统学会（ISTVS 1977）标准中，车轮侵入深度被定义为从车轮的最低点到未扰动的土壤表面的距离。

3.1 几何模型

选择某型工程车常用轮胎，轮胎宽度为52.07 cm，轮胎外径为180 cm，如图3 所示。软土地面为规则长方体区域，长度为6 m，宽度为3 m，高度为2 m，如图4 所示，同时选取软土表面为零平面。经过颗粒尺寸敏感性分析，软土地面物质点颗粒直径为轮胎宽度的1/32。

图3 车轮几何模型Fig.3 Geometry model of wheel

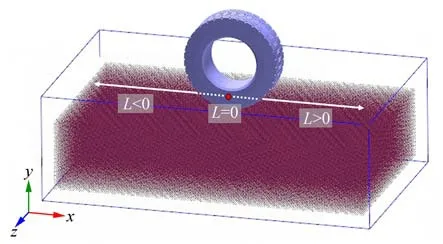
图4 车轮-软土侵入计算几何模型Fig.4 Geometry model of wheel and soft-soil interaction calculation

3.2 物理力学参数、初始和边界条件

选取某黏性土作为典型软土地面，该黏性土物理力学参数如表1 所示［25］。分析不同车轮载重（1 000 kg、3 000 kg、5 000 kg、7 000 kg、9 000 kg和11 000 kg）、弹性模量（4 MPa、8 MPa、12 MPa、16 MPa、20 MPa 和24 MPa）、黏 聚力（5 kPa、10 kPa、15 kPa、20 kPa 和25 kPa）和摩擦角（10°、15°、20°、25°和30°）时，车轮侵入软土地面的深度。软土地面力学参数变化涵盖了《工程勘察通用规范》（GB 55017-2021）中黏性土、粉土和部分砂土的力学参数取值范围［26］。计算过程中，每次变化一个参数，其余参数按表1 中数值取值。当车轮气压达标时，车轮变形量比软土变形量低二到三个量级，车轮可采用线弹性本构模型。当车轮变形远小于软土变形，可简化车轮中橡胶、钢丝、帘布以及带束等材料各自的力学特性，采用加权平均后整体车轮的力学特性，弹性模量大于470 MPa，泊松比约为0.48。

表1 物理力学参数Tab.1 Physical and mechanical parameters

软土地面的初始地应力与土壤密度、深度相关，且初始位移为0。软土地面四周和底边界采用法向位移约束，位移为0。

4 计算结果

4.1 车轮载重的影响

改变车轮载重（1 000 kg、3 000 kg、5 000 kg、7 000 kg、9 000 kg 和11 000 kg），分析车轮-软土相互作用规律。以3 000 kg 和11 000 kg 载重为例，车轮侵入软土的位移云图分别如图5 和图6所示。当载重为3 000 kg 时，车轮侵入软土深度大约为4.61 cm。当载重为11 000 kg 时，车轮侵入软土深度大约为31.27 cm。随载重增加，车轮侵入深度逐渐增大，车轮径向（进行方向）和轴向软土受挤压向上隆起。软土隆起范围和高度与载重正相关，车轮侵入软土过程中，三维效应非常明显。

图6 车轮侵入软土位移云图（11 000 kg）Fig.6 Displacement of soft-soil under wheel load（11 000 kg）

不同载重条件下，软土表面压应力在车轮径向和轴向的差异较大。选取车轮径向对称面在软土表面的投影线及其延伸线为特征线，车轮中心的投影点为0 m 位置。载重变化后，特征线上的软土表面压应力曲线如图7 所示。不同载重时，车轮对软土的压应力均以车轮中心投影点为对称点接近对称分布，对称点（车轮中心的投影点）压应力最大，压应力轮廓随载重增加而扩大，说明车轮接触软土的面积逐渐增大。随载重增加，压应力最大值逐渐增大，分别为15.39 kPa、31.47 kPa、46.09 kPa、59.19 kPa、70.30 kPa 和78.65 kPa。远离对称点时，压应力先快速降低后小幅增加，这与直接接触车轮的软土受压变形后侧向挤压相邻软土产生的应力有关。

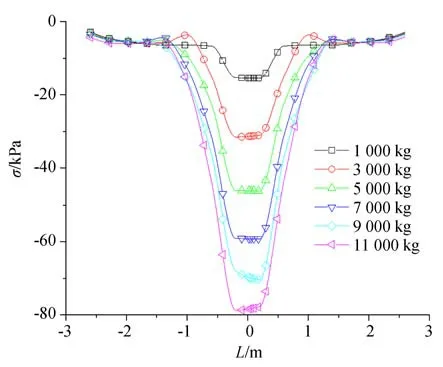
图7 不同载重时软土表面压应力Fig.7 Stress of soft-soil surface under different wheel loads

不同载重条件下，车轮侵入软土最大深度（umax）和最大压应力（σmax）变化曲线如图8 所示。随车轮载重增大（1 000 kg～11 000 kg），车轮侵入软土最大深度分别为1.59 cm、4.61 cm、9.72 cm、16.19 cm、24.01 cm 和31.27 cm。载重增大至11 倍，侵入深度增大至19.67 倍，侵入深度相对改变量约为179%。当载重小于5 000 kg 时，车轮侵入软土最大深度随载重非线性增加。当载重大于5 000 kg 时，车轮侵入软土最大深度几乎随载重线性增加。此外，当载重小于5 000 kg时，最大压应力几乎与载重线性相关。当载重大于5 000 kg 时，最大压应力随载重非线性增加。随侵入深度增加，车轮-软土接触面积也持续增加，但最大压应力增加趋势并未改变，说明载重是侵入深度的关键参数之一。同时由于侵入深度与载重的关系是单调正相关且非线性不强，因而在现场车辆通行性快速评估过程中载重变化引起的侵入深度比较容易预测，并可近似按线性拟合。

图8 最大侵入深度-载重-最大压应力关系Fig.8 Relationship between maximum intrusion depth，loads，and maximum stress

4.2 软土弹性模量的影响

改变软土弹性模量（4 MPa、8 MPa、12 MPa、16 MPa、20 MPa 和24 MPa），分析车轮-软土相互作用规律。选取车轮径向对称面在软土表面的投影线及其延伸线为特征线，车轮中心的投影点为0 m 位置。弹性模量变化后，特征线上的软土表面压应力曲线如图9 所示。不同弹性模量时，车轮对软土的压应力均以车轮中心投影点为对称点接近对称分布，对称点（车轮中心的投影点）压应力最大，压应力轮廓线几乎不变，说明车轮接触软土的面积也几乎不变。随弹性模量载重增加，压应力最大值逐渐降低，分别为51.80 kPa、48.90 kPa、48.55 kPa、48.40 kPa、48.30 kPa 和48.20 kPa。车轮径向压应力减增拐点位置几乎不变，说明与车轮直接接触的软土变形有限，相邻的软土受侧向挤压程度相似。

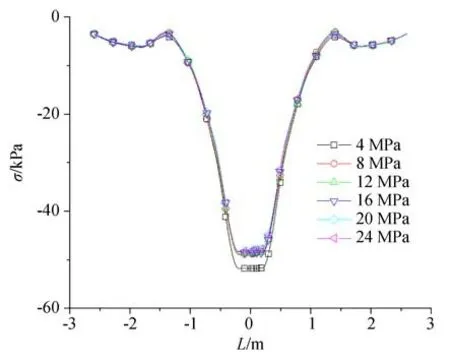
图9 不同弹性模量时软土表面压应力Fig.9 Stress of soft-soil surface with different elastic modulus

不同弹性模量条件下，车轮侵入软土最大深度（umax）和最大压应力（σmax）变化曲线如图10 所示。随弹性模量增大（4 MPa～24 MPa），车轮侵入软土最大深度分别为14.68 cm、13.02 cm、11.92 cm、11.31 cm、10.95 cm 和10.83 cm。弹性模量增至6 倍，侵入深度约降低至71.43%，侵入深度相对改变量约为23%。车轮侵入软土最大深度和最大压应力均随弹性模量增大非线性降低。当弹性模量大于8 MPa，最大压应力几乎不变，即车轮-软土地面接触面积也几乎不变，说明软土处于弹性变形阶段，尚未发生塑性变形。当弹性模量较大时（＞10 MPa），增大弹性模量后，最大侵入深度降低约9%。当载荷保持一定时，对处于弹性变形阶段的软土，弹性模量变化对车轮侵入深度影响有限。同时由于侵入深度与弹性模量的关系是单调负相关且变化量不大，因而在现场车辆通行性快速评估过程中弹性模量对侵入深度的影响比较容易预测。

图10 最大侵入深度-弹性模量-最大压应力关系Fig.10 Relationship between maximum intrusion depth，modulus，and maximum stress

4.3 软土强度的影响

车轮侵入软土过程中，软土逐渐从弹性变形阶段进入塑性变形阶段，侵入深度与软土塑性变形密切相关，因而软土强度参数对侵入深度有较大影响。改变软土强度参数，黏聚力c（5 kPa、10 kPa、15 kPa、20 kPa 和25 kPa）和摩擦角φ（10°、15°、20°、25°和30°），分析车轮-软土相互作用规律。选取车轮径向对称面在软土表面的投影线及其延伸线为特征线，车轮中心的投影点为0 m位置。以摩擦角10°为例，改变黏聚力（5 kPa、10 kPa、15 kPa、20 kPa 和25 kPa），特征线上的软土表面压应力曲线如图11 所示。不同黏聚力时，车轮对软土的压应力均以车轮中心投影点为对称点接近对称分布，对称点（车轮中心的投影点）压应力最大，压应力轮廓线逐渐缩小，说明车轮接触软土的面积逐渐减小。随黏聚力增加，压应力最大值逐渐增大，分别为48.90 kPa、58.87 kPa、62.39 kPa、63.21 kPa 和63.27 kPa。车轮径向压应力减增拐点位置与黏聚力大小负相关，黏聚力越大拐点距离中心点越近，说明车轮相邻软土受侧向挤压的变形范围逐渐减小。

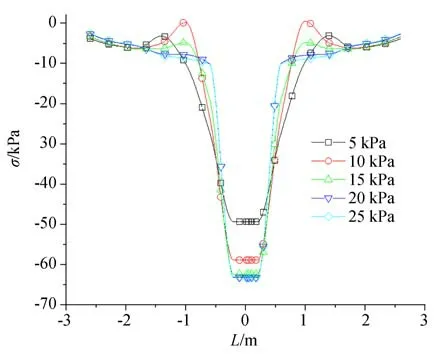
图11 不同黏聚力时软土表面压应力Fig.11 Stress of soft-soil surface with different cohesion

当摩擦角为10°时，改变黏聚力大小，车轮侵入软土最大深度（umax）和最大压应力（σmax）变化曲线如图12 所示。不同黏聚力条件下，车轮侵入软土最大深度分别为13.02 cm、5.83 cm、4.42 cm、3.80 cm 和3.36 cm。黏聚力增至5倍，侵入深度约降低至25.77%，侵入深度相对改变量约为78%。车轮侵入软土最大深度随黏聚力增大非线性降低，黏聚力越小，侵入深度对黏聚力越敏感。最大压应力随黏聚力增大先增加然后趋于稳定，即黏聚力改变后车轮-软土接触面积逐渐降低至定值。

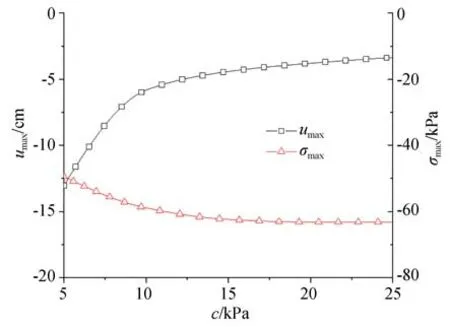
图12 最大侵入深度-黏聚力-最大压应力关系Fig.12 Relationship between maximum intrusion depth，cohesion，and maximum stress

以黏聚力5 kPa 为例，改变摩擦角（10°、15°、20°、25°和30°），特征线上的软土表面压应力曲线如图13 所示。不同摩擦角时，车轮对软土的压应力均以车轮中心投影点为对称点接近对称分布，对称点（车轮中心的投影点）压应力最大。随摩擦角增加，压应力最大值逐渐增大，分别为48.90 kPa、55.38 kPa、62.79 kPa、69.59 kPa 和69.89 kPa。车轮径向压应力减增拐点位置与摩擦角大小负相关，摩擦角越大拐点距离中心点越近，说明车轮相邻软土受侧向挤压的变形范围逐渐减小。

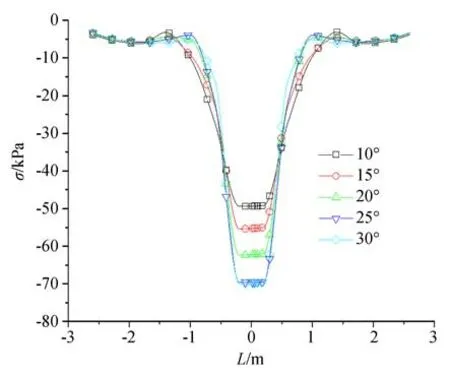
图13 不同摩擦角时软土表面压应力Fig.13 Stress of soft-soil surface with different friction angles

当黏聚力为5 kPa 时，改变摩擦角大小，车轮侵入软土最大深度（umax）和最大压应力（σmax）变化曲线如图14 所示。不同摩擦角时，车轮侵入软土最大深度分别为13.02 cm、6.39 cm、4.15 cm、3.00 cm 和2.40 cm。摩擦角增至3 倍，侵入深度约降至18.42%，侵入深度相对改变量为181%。车轮侵入软土最大深度随摩擦角增大非线性降低，摩擦角越小，侵入深度对摩擦角越敏感。最大压应力随摩擦角增大先增加然后保持一定。

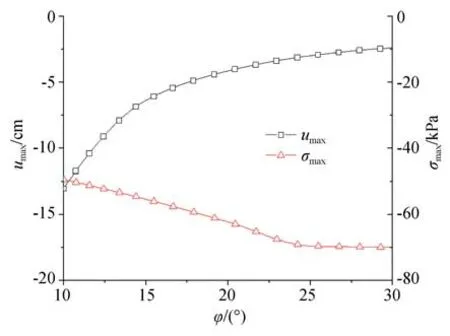
图14 最大侵入深度-摩擦角-最大压应力关系曲线Fig.14 Relationship between maximum intrusion depth，friction angle，and maximum stress

当黏聚力变化或摩擦角单独变化时，最大侵入深度均非线性单调变化。本文中摩擦角对车轮侵入深度的影响更大，这是由于压应力大于黏聚力，软土抗剪强度与黏聚力呈线性关系，而与摩擦角为正切函数关系。当压应力和黏聚力处于同一量级时，侵入深度主要受黏聚力和摩擦角共同影响，且对摩擦角更为敏感。当压应力量级高于黏聚力时，侵入深度主要受摩擦角影响。当压应力量级低于黏聚力时，侵入深度主要受黏聚力影响。这种双因素影响比载重或弹性模量单因素影响更为复杂。进一步，黏聚力和摩擦角共同决定的软土抗剪强度可能更为直接的影响车轮侵入深度。准静态条件下，分析车轮侵入深度与软土抗剪强度（τmax=c+σmaxtanφ）的关系，如图15 所示。随软土抗剪强度的增加，车轮侵入深度非线性降低。当软土最大剪应力较低时，车轮侵入深度有显著变化，这与单独考虑黏聚力或摩擦角时的规律相似。软土抗剪强度增至3.31 倍，侵入深度约降低至18.45%，侵入深度相对改变量约为164%，与摩擦角的影响处于同一量级。

图15 侵入深度-最大剪应力关系Fig.15 Relationship between intrusion depth and maximum shear stress

装备通行性评估中，通常需要快速得到不同软土地面上车轮的侵入深度。软土强度特性对侵入深度的非线性影响非常明显，但抗剪强度往往不容易在现场直接获得，而黏聚力和摩擦角可以通过现场快速勘测解译获得。通过图12、图14和图15 分析可得，侵入深度与抗剪强度的关系与其单独考虑黏聚力或摩擦角的关系相似。因此，当现场软土抗剪强度不容易获得时，可以考虑通过黏聚力和摩擦角的变化，间接获得车轮侵入深度。以车轮载荷为6 000 kg 例，改变黏聚力（5 kPa、10 kPa、15 kPa、20 kPa 和25 kPa）和摩擦角（10°、15°、20°、25°和30°），建立黏聚力、摩擦角和侵入深度构成的三维曲面，如图16 所示。侵入深度最大值和最小值在曲面对角线的两端，最大值附近区域侵入深度梯度较大。当黏聚力大于10 kPa 且摩擦角大于15°时，侵入深度变化有限。因此，基于载重与侵入深度近似线性的关系，建立某型装备不同载重条件下的软土侵入深度曲面数据库，可为快速确定现场测量软土关键力学参数提供理论依据，有助于优化装备通行性评估策略，提高装备通行性评估效率。

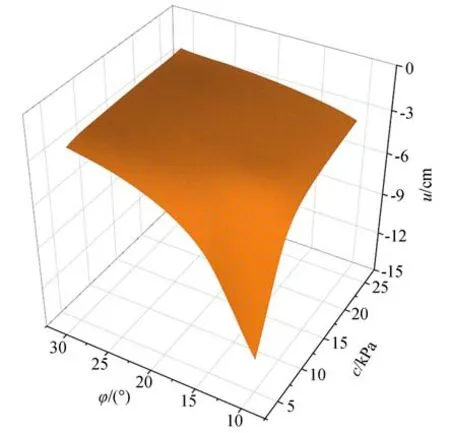
图16 黏聚力-摩擦角-侵入深度关系曲面Fig.16 Relationship between cohesion，friction angle and intrusion depth

5 结论

本文提出了CDEM-MPM 耦合计算方法，利用CDEM 模拟车轮，利用MPM 模拟软土，可有效模拟弹性车轮侵入软土过程中的大变形问题，同时降低了数值模拟所需的计算成本。通过建立车轮-软土地面耦合模型，采用CDEM-MPM耦合计算方法，数值模拟了车轮和软土地面相互作用过程，定量分析了车轮载重、软土弹性模量、软土强度参数（黏聚力、摩擦角）与软土表面压应力、侵入深度等参数之间的关系，获得了车轮侵入软土深度的变化规律。结论如下：

（1）当载重增大11 倍，侵入深度增大至19.67 倍，侵入深度相对改变量约为179%。载重是影响侵入深度的关键参数之一。车轮侵入深度与车轮载重接近线性正相关，因而在现场车辆通行性快速评估过程中载重引起的侵入深度变化比较容易预测，并可近似按线性拟合。

（2）当弹性模量增至6 倍，侵入深度降低至71.43%，侵入深度相对改变量约为23%。同时，随弹性模量持续增加，侵入深度值降低量小于9%。当载荷保持一定时，对处于弹性变形阶段的软土，侵入深度值变化不大。车轮侵入深度对弹性模量不敏感，因而在现场车辆通行性快速评估过程中弹性模量引起的侵入深度变化也比较容易预测。

（3）当黏聚力增至5 倍，侵入深度降低至25.77%，侵入深度相对改变量约为78%。摩擦角增至3 倍，侵入深度降低至18.42%，侵入深度相对改变量约为181%。黏聚力和摩擦角共同影响的抗剪强度增至3.31 倍，侵入深度降低至18.5%，侵入深度相对改变量约为164%。侵入深度受到两个强度参数的共同影响，且对摩擦角更为敏感，这导致侵入深度较难实现现场预测。

基于CDEM-MPM 耦合数值计算方法，建立某型号装备不同载重条件下的软土侵入深度三维曲面数据库，可为软土地面装备通行性评估中现场待测的关键力学参数提供理论依据。此外，基于该数值计算方法，下一步还可分析车轮不同运动状态与软土侵入深度的关系，有助于优化装备通行性评估策略，提高装备通行性评估效率。