旋转不变的2D 视图-3D 点云自编码器
刘贤颖,吴秋遐*,康文雄,李玉琼
(1.华南理工大学 软件学院,广东 广州 510006;2.华南理工大学 自动化科学与工程学院,广东 广州 510641;3.中国科学院 力学研究所,北京 100190)
1 引言
随着三维扫描技术的不断发展与快速普及,人们可以实现对真实物体表面进行点采样,这些采样数据称为三维点云。点云包含物体的坐标,法向量等基本信息,具有较高的灵活性和适用性,在建筑、机械、自动驾驶[1]等领域中有着重要的应用价值。近年来,借助广泛的监督信息,深度学习在点云分类、分割、目标检测等任务中取得了显著的成果[2-7]。然而,监督学习需要大量的人工标注来获取监督信息,同时限制模型的泛化能力。因此,无监督学习是获得通用点云表征的一个有吸引力的方向。另外,在现实工程应用中,点云不可避免发生旋转变换,呈现出任意的空间位置和姿态,导致模型性能急剧下降。因此,从未标注的数据中学习旋转鲁棒的通用点云表征是一个艰巨的挑战。
在深度学习中,自动编码器(Auto-encoder)是无监督学习点云表征的重要架构。现有的一些研究工作[8-14]在编解码器的结构上进行无监督的点云表征学习。典型的方法是将三维重建作为辅助任务,使用自动编码器将点云编码为特征,然后将特征 解码重建点 云。FoldingNet[15]提出了一种折叠操作,将标准二维网格变形到点云表面,但是它的缺陷是特征学习能力较弱。为了获取更精细的点云特征,一些方法联合利用局部结构信息进行全局形状的重建[10-11]。文献[10]采用分层自注意力机制对局部区域内多个尺度的几何信息同时进行编码,通过局部到全局的重构来同时学习点云的局部和全局结构。文献[11]引入多角度分析来理解点云,通过语义局部自监督来学习局部几何和结构。除了对点云空间结构的学习,一些研究致力于挖掘点云自身潜在的语义信息[12-13],通过对比度量的思想建模抽象的深层次信息,以学习点云潜在的语义信息。以上方法仅在点云的三维模态进行学习,这会使得模型的表达能力在一定程度上受到限制。为了学习点云多模态的信息,CrossPoint[14]提出一种2D-3D 的跨模态点云表征学习方法,但其需要提前准备好点云的二维图像数据,在实际应用中会增加大量的计算。
尽管以FoldingNet[15]为主的一系列点云 自编码器可以有效地学习点云表征,但它们大多是在预先对齐的合成数据集上进行评估的,而在实际应用中很难访问对齐良好的点云,一旦点云的姿态发生旋转变化,这些网络性能会急速下降。在无监督点云表征学习中,解决旋转干扰问题的一个直观方法是通过考虑所有可能的旋转来对训练数据进行扩充,再输入无监督网络进行训练。但由于点云旋转的搜索空间无穷大且深度网络的学习能力有限,深度网络无法适应任意的旋转,并且点云数据被旋转增强后,通过其形状挖掘语义信息将变得困难。一些研究人员提出了无监督学习中的旋转问题解决方案[8-9],PPFFoldNet[8]使用基于手工制作的三维特征描述符组成的局部面片表示点云,并通过局部面片的重建实现无监督学习。这种通过局部邻域内边角关系构成的描述符严格刻画了点云局部旋转不变的特征。但由于丢失点云原始坐标信息,特征学习不充分,模型在下游任务的评估效果并不理想。ELGANet-U[9]在设计局部旋转不变描述符的基础上增加了全局旋转不变信息,使用图卷积网络(Graph Convolution Networks,GCN)构成的对齐模块学习点云旋转不变的坐标,通过重建对齐后点云补充全局信息。但GCN 的灵活性和可拓展性较差,文献[16]指出在缺乏标签监督的情况下,GCN 的性能会有比较严重的下降,这会降低学习到的点云表征在下游任务中的性能。
针对上述问题,本文提出了一个旋转不变的2D 视图-3D 点云自编码器(Rotation-invariant 2D views-3D Point Clouds Auto-encoder,RI 2D-3D AE),极小化旋转影响并且同时利用点云及其视图充分提取信息。主要创新点和贡献有:(1)针对旋转问题,设计局部融合全局的旋转不变特征转换策略。对于局部表示,利用手工设计特征对输入点云进行转换,生成旋转不变的点云表征;对于全局表示,提出一个基于主成分分析的全局对齐模块(Principal Component Analysis Global Alignment,PCA-GA),将旋转点云对齐同一姿态下,在补充全局信息的同时排除旋转干扰。(2)针对编码器,设计局部和非局部特征提取模块(Local and Non-local Module,LNLM),充分提取点云的局部空间特征和非局部上下文相关性,并建模不同层次特征之间的语义一致性。(3)提出一个基于PCA 对齐的2D-3D 重构的解码方法,重建对齐后的三维点云和二维视图,使编码器输出的点云表征集成来自3D 点云和2D 视图的丰富学习信号。
2 旋转不变的点云自编码器
2.1 点云自编码器模型架构
本文提出的旋转不变的2D 视图-3D 点云自编码器如图1 所示,其主要包括旋转不变的局部和非局部特征编码器(Rotation-invariant Local and Non-local Encoder,RI-LNL Encoder)和基于主成分分析对齐的2D-3D 重构解码器(PCA 2D-3D Reconstruction Decoder)。
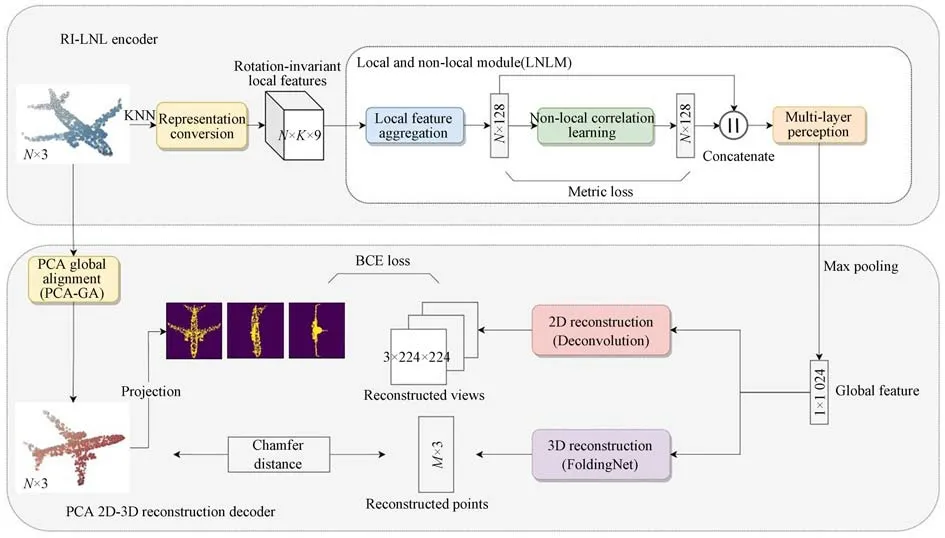
图1 旋转不变的2D 视图-3D 点云自编码器结构示意图Fig.1 Structure diagram of rotation-invariant 2D views-3D point clouds auto-encoder
在特征编码阶段,首先将点云转换为旋转不变的局部特征描述符,然后从局部和非局部聚合为输入点云的全局表征,并通过度量学习建模特征之间的语义一致性。在特征解码阶段,首先将点云进行全局对齐,对齐后的点云不受旋转干扰,然后通过两个重建分支分别重建对齐后的三维点云及其二维视图。
2.2 旋转不变的局部和非局部特征编码器
2.2.1 点云的局部旋转不变特征转换
编码器的输入是一个具有N=1 024 个点的无序点云其 对应的法向量集表示为局部结构对点云表征学习至关重要,其包含点云的空间几何信息。大多数网络直接在原始点云坐标上学习局部特征,这很容易受到旋转的干扰。
受三维局部特征描述符PPF[8]启发,本文设计了一个基于局部邻域中的相对距离和角度的旋转不变特征描述符来对点云进行特征转换,如图2 所示。与其他在单一坐标系下构建的特征描述符不同,本文在局部和全局坐标系中收集特征,使描述符具有更丰富的特征信息和更强的旋转鲁棒性。对于一个查询点pi,对应k=64 个近邻点,pi与其近邻点形成k个点对。为了描述点之间的相对位置,在每个点对(pi,pij)上建立局部坐标系(ui,vi,wi):

图2 手工制作的旋转不变特征描述符Fig.2 Handcrafted rotation-invariant features
2.2.2 局部和非局部特征提取模块
为了进一步聚合局部领域内的空间几何信息,并学习长距离的上下文相关性,设计局部和非局部的特征提取模块,其结构如图3 所示。

图3 局部和非局部的特征提取模块及特征聚合层结构图Fig.3 Structure diagram of local and non-local module and feature aggregation layer
LNLM 首先对转换后的特征图Mi通过特征聚合层(Feature Aggregation,FA)得到点pi的局部特征fai,FA 的计算过程如下式所示:
其中:h和h′是多层感知机(Multi-layer Perceptron,MLP)。由于MLP 只能独立处理每个转换特征mi,j,不能捕捉KNN 邻域中各点的信息。因此使用卷积层聚合局部邻域信息得到聚合向量vi,其补充了邻域内其它点的信息。点云P=的局部特征表示为
局部特征Fa仅关注欧几里得空间中的局部邻域,忽略了遥远但相似点之间的非局部相关性。DGCNN[4]发现语义相似点的特征在特征值空间中的距离是相近的。沿着这个方向,对于Fa的每个特征向量fai,搜索与其距离最近的k个特征向量,然后同样通过FA 得到点pi的非局部特征fbi,则点云P=的非局部特征表示为
最后,连接Fa与Fb并通过MLP 和池化层聚合为点云全局表征g。
2.2.3 局部-非局部-全局语义一致性建模
由于缺乏人工标签训练,无监督学习通常无法从点云中学习类别语义信息。为了增强网络学习到的点云表征,基于度量学习的思想建模局部-非局部-全局之间共享的语义知识,以挖掘点云自身潜在的具有区分性的语义信息。具体来说,一个点云P输入编码器得到三个特征:局部特征,非局部特征,全局特征向量g,这三个不同抽象层次的特征在语义上是一致的,都属于点云P的类别并且区别于其他点云。由此构建语义一致性度量损失:
其中:φ和φ是两个映射函数,负责将维度不一样的特征映射到相同的特征空间,通过MLP 实现;s是一个常数值。式(6)表示点云样本P中的一个点pi的特征fi∈{fai,fbi}与P对应全 局特征g的距离尽量小,而与其它点云样本的全局特征gk的距离尽可能大;式(7)表示对点云P中的每个点计算的度量损失进行求和,以此来捕获不同层次特征共享的底层语义知识。
2.3 基于主成分分析对齐的2D-3D 重构解码器
2.3.1 基于主成分分析的全局对齐模块
解码器的目标是通过全局形状重建来学习全局结构。然而,当重建的目标点云受到旋转干扰,会极大地影响重建效果。本文设计PCAGA,通过PCA 学习点云的固有坐标帧,并将重建的目标点云对齐到由固有帧构成的新坐标系下,以生成旋转不变的点坐标,这保证了重建的旋转鲁棒性。
其中:Pc是原始点云P中心化的结果,U是左奇异矩阵,Σ是对角矩阵,V=[v1,v2,v3]是一个3×3 的正交矩阵,代表从原始点云内提取中的固有坐标帧。对于同一个点云的所有旋转克隆,它们的固有坐标帧是相同的。为了实现旋转不变性,将点从原始模型转换为新建立的全局坐标系:
其中,P′是旋转不变的点坐标。PCA-GA 可以将无限旋转姿态对齐到固定姿态,同时保留原始点云信息,从根本上降低解码器对旋转点云的重建难度,为整个网络架构提供了旋转不变的全局信息。
2.3.2 2D 视 图-3D 点云重建
当前的自动编码器大多仅在三维重建中学习全局结构,这会使得模型的表达能力在一定程度上受到限制。在现实世界中,三维物体的二维视图具有丰富的信号,人眼能够通过2D 视图理解3D 物体。由此可以推测,在点云无监督学习中,结合二维视图训练模型,可以增强网络编码能力,促进模型对3D 世界的有效理解。受此启发,在PCA 对齐的基础上,本文提出一个2D 视图-3D 点云重构的解码方法。
对于解码器输出的全局表征g,设计两个分支执行不同的重建任务。在其中一个分支进行三维点云自重构,采用文献[8]中基于折叠的解码器D(·)将标准2D 网格变形为以全局表征g为条件的点云3D 坐标Pr:
3D 重建损失定义为倒角距离:
注意,与其他解码器不同,解码器不直接重建输入点云P,而是经对齐后的旋转不变的点坐标P′。
在另一个分支进行点云的视图重建任务:生成点云P′的俯视图、侧视图和前视图,使用反卷积层在全局表征g基础上重建三个视图。由于生成的视图是二值图像,因此2D 重建损失定义为二值交叉熵(Binary Cross-Entropy,BCE):
其中:xi是点云P′的一个视图,yi是反卷积层输出的重建视图。式(13)计算了一个视图的重建损失,在实际训练中需要重建三个视图。
2D 重建分支不需要提前准备好2D 图像,而是直接将点云投影到PCA-GA 提取到的坐标系下,以生成点云在不同方向上的视图,该投影过程的成本在时间和计算上都是微乎其微的。同时,PCA-GA 提取到的三个坐标轴是点云信息量最大的维度,在该坐标轴下投影得到的点云视图尽可能保留了点云的主要信息,降低了模型学习2D 视图信息的难度。
2.4 目标函数
结合编码器的语义一致性度量损失和解码器的2D-3D 重建,得出点云自编码器的训练目标:
经过充分训练后,全局特征表示g可以用作点云的高维表示,并可用于下游应用。该表征保证了旋转不变性,更适用于具有旋转扰动的场景。此外,其以自我监督的方式集成了来自3D点云和2D 视图的丰富学习信号。另外,由于三维重建分支是从二维网格折叠到三维点云的架构,视图重建任务在一定程度上能够促进三维点云的重建。
3 实验结果与分析
3.1 实验数据集
本文在合成数据集ModelNet40[17]、真实数据集ScanObjectNN[18]中评估提出的网络。
ModelNet40 包括来自40 个人造对象类别的12 311 个CAD 模 型,其 中,9 843 个CAD 模型用于培训,2 468 个模型用于测试。
ScanObjectNN 是一个更真实、更具挑战性的3D 点云数据集,它由从真实室内扫描中提取的对象组成。它包含来自15 个类别的2 902 个对象,其中2 319 个用于训练,583 个用于测试。ScanObjectNN 有多个不同的变体,在本实验中使用常用的变体OBJ_BG(添加背景干扰和遮挡),以及难度最高的变体PB_T50_RS(添加平移和旋转扰动)。
3.2 实验设置
在无监督学习中,网络通过执行精心设计的训练任务,可以获得无标签的点云表征。衡量无监督学习质量的一个常见指标是生成表征的线性可分性。因此,本文使用线性支持向量机(Support Vector Mechine,SVM)分类器进行对象分类,作为评估特征表示能力的下游任务。具体来说,在对象分类实验中,采用OneVsRest 策略,以linearSVM 函数为内核,从自动编码器获得的全局特征中训练了一个线性SVM 分类器。根据分类精度来评估的点云表征的可分辨性。
另外,为了有效评估网络的旋转鲁棒性,在三种情况下进行实验,分别为原始训练集和测试集(z/z),原始训练集和任意3D 旋转增强的测试集(z/SO3),任意3D 旋转增强的训练集和测试集(SO3/SO3)。
在实验中,使用ADAM optimizer 在NVIDIA RTX 2080 Ti GPU 上训练网络,初始学习率为0.000 1,批量大小为16。每20 个epoch,学习率降低20%,模型训练200 个epoch。
3.3 无监督点云分类结果分析
首先在合成数据集ModelNet40 上测试RI 2D-3D AE,并与最先进的无监督方法进行比较,分类精度如表1 所示。

表1 ModelNet40 数据集上不同方法的分类精度Tab.1 Classification accuracy of the different methods on ModelNet40
从实验结果可以看出,在测试集随机旋转增强的情况下(z/SO3),常规的有监督方法[2-4]和无监督方法[13-15]的分类准确率出现了严重的衰减,当前效果最好的无监督方法PointGLR[13]仅能取得14.34% 的准确率,而本文提出的RI 2D-3D AE 在不同的环境中始终保持优异的性能。对于旋转鲁棒的竞争方法,RI 2D-3D AE 显著优于ModelNet40 下的所有无 监督竞争对 手[8-9]。RI 2D-3D AE 不仅保证了表征的旋转不变性,其所学习到的表征也有较高的可区分性,使分类准确率在三种情形下都达到了当前领先的水平。
另外,在引入旋转增强后,即在SO3/SO3 情况下,对比常规的有监督方法,无监督方法的性能并没有很大的提升。DGCNN[4]在训练集引入旋转增强后,分类准确率从20.60% 上升到81.10%,而FoldingNet[15]仅 从14.18% 上升到43.13%。这是由于无监督学习中目标函数旨在完成点云的重构,并不是直接作用在分类损失上,点云数据被旋转增强后,通过其形状挖掘语义信息将变得困难。在这种情形下,基于自重建的无监督方法的性能将出现明显衰减。因此在无监督学习中,数据增强不能解决旋转干扰问题。相比之下,RI 2D-3D AE 在SO3/SO3 情况下生成的表征仍然保持着最优的区分性。
考虑到ModelNet40 中的对象是姿势相似且无噪声的CAD 模型,与真实世界的数据有较大差距。为了证明RI 2D-3D AE 具有推广到实际应用的能力,在真实数据集ScanObjectNN 上评估模型,实验结果如表2 所示。可以看出,由于真实数据集中存在不少干扰因素,导致大多数方法的性能比其在 ModelNet40 数据集上的出现一定程度的衰减。而RI 2D-3D AE 在三种情况下依旧保持较高水平的表现,并且优于其他先进的无监督方法,证明了其表征学习方法的鲁棒性和实际应用价值。
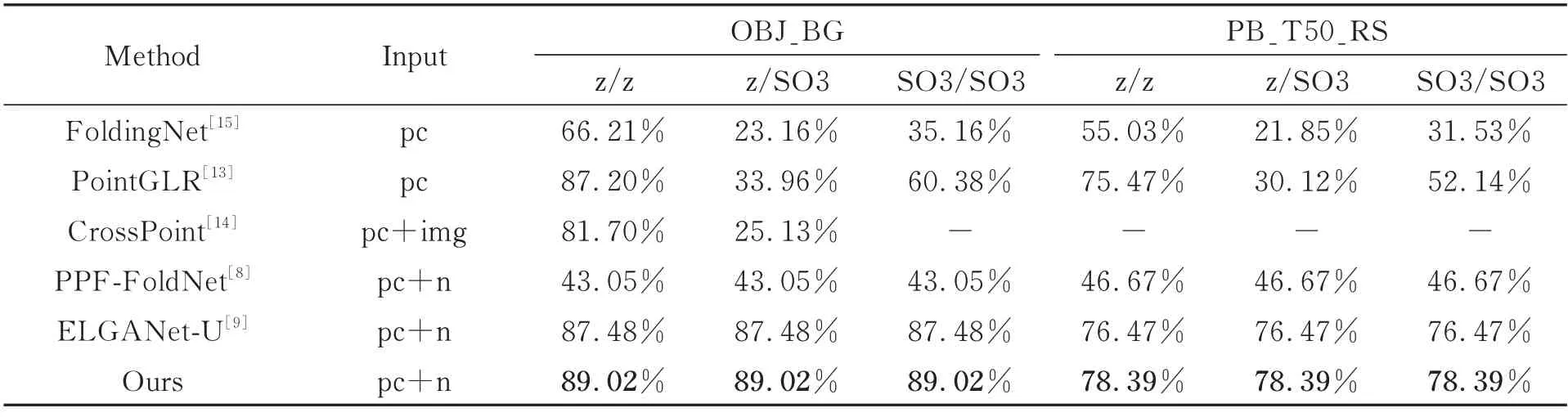
表2 ScanObjectNN 数据集上无监督方法的分类精度Tab.2 Classification accuracy of the unsupervised methods on ScanObjectNN
3.4 消融实验
为了评估RI 2D-3D AE 中各个模块和架构的贡献,将模块逐个分离来训练模型,并在z/SO3 情况下的ScanObjectNN(OBJ_BG)数据集上评估线性SVM 分类器。首先固定解码器为3D 重建,验证编码器中的各个模块,实验结果如表3 所示。

表3 在ScanObjectNN 上编码器模块的消融结果Tab.3 Ablation results of encoder on ScanObjectNN
基线模型A 可以被视为FoldingNet[15]的 变体,该模型仅由在局部坐标系和全局坐标系中分别计算的特征描述符f1,f2,以及局部特征学习Fa组成,分类精度较低。在增加非局部相关性特征Fb后(模型B),准确率较基线上升了12.18%,这有力证明了非局部特征学习模块的有效性。在增加局部-非局部-全局语义一致性损失Lmetric后(模型D),准确率较模型B 上升1.37%。模型C去除了在全局坐标系中计算的特征描述符f2,准确率较模型D 有所下降。结果说明,编码器的各个主要模块对提升点云全局表征能力均具有重要作用。
固定编码器,验证解码器中的各个模块的有效性,实验结果如表4 所示。从结果看,在加入全局对齐模块PCA-GA 后(模型E),准确率较模型D 上升了0.68%,说明PCA-GA 能有效提升真实场景下的旋转鲁棒性。最后,加入2D 视图重建模块得到完整的模型F,也就是本文提出的RI 2D-3D AE,在ScanObjectNN 数据集上获得了显著的效果。

表4 在ScanObjectNN 上解码器模块的消融结果Tab.4 Ablation results of decoder on ScanObjectNN
为了进一步验证点云2D 视图在特征编码中的有效性,研究2D 视图重建分支的贡献,使用不同视角的视图对模型进行训练,并在z/SO3 情况下的ModelNet40 中评估线性SVM 分类器。实验结果如表5 所示。从结果看,即使使用单个方向上的2D 视图,也可以产生更好的线性分类结果。相对于其它视图,俯视图对结果的提升最大,为了分析原因,部分点云对象及其视图可视化如图4 所示。

表5 在ModelNet40 上各个视图的消融结果Tab.5 Ablation results concerning each view on Model-Net40
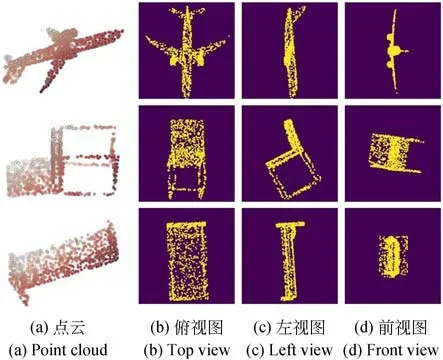
图4 部分点云对象及其视图的可视化Fig.4 Visualization of partial point cloud objects and their views
从图4 可以看出,一些点云的俯视图反映出了3D 对象的大部分主要信息,另一些需要结合三个视图来推测原始点云。在点云自编码器中加入视图重建分支后,相当于建立起二维视图与三维对象的联系,引导编码器向特征信息更多的方向进行学习,增强网络编码能力。
3.5 可视化结果
为了更好地展示表征的可区分性,使用t-分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)聚类对学到的点云表征进行可视化。首 先FoldingNet[15]在z/SO3 情 况下的ModelNet40 上生成的部分类别表征可视化结果如图5 所示。可见在旋转干扰情况下,FoldingNet 生成的各类别表征难以区分。

图5 FoldingNet 表征的t-SNE 聚类可视化Fig.5 t-SNE clustering visualization of FoldingNet
本文提出的RI 2D-3D AE 可视化结果如图6 所示。即使在样本随机旋转的情况下,编码器生成的点云表征的类间距离仍较大,可区分性高,证明了表征具有良好的可区分性和旋转鲁棒性。
从图6 还看出,比较难区分的类别是Desk(浅蓝色)和Table(灰色),原因在于这两类物体特征高度相似,即使是人类也无法轻易区分。图7 为错误分类样本示例。本文提出的算法目前还不能区分这些高度相似的不同类别样本,这也是未来的一个优化方向。

图6 RI 2D-3D AE 表征的t-SNE 聚类可视化Fig.6 t-SNE clustering visualization of RI 2D-3D AE

图7 部分错误分类样本Fig.7 Examples of misclassification
4 结论
本文针对现有点云自编码器存在的旋转干扰和特征提取不足问题,提出一个旋转不变的2D 视图-3D 点云自编码器。针对旋转干扰问题,对输入点云进行局部和全局的特征转换,将点云转换为旋转不变的特征表示。针对特征提取问题,设计局部和非局部特征提取模块,并建模不同层次特征的语义一致性,增强了表征的空间和语义信息;设计二维视图和三维点云重建任务,结合二维视图训练模型,可以增强网络编码能力,促进模型对3D 世界的有效理解。实验结果证明,本算法在随机旋转的合成数据集Model-Net40 和真实数据集ScanObjectNN 上的识别精度分别为90.84%和89.02%,学习到的点云表征的可辨别性和旋转鲁棒性优于其他先进的无监督方法。

