ICESat-2 数据背景光子特性及滤波方法研究

谢 欢，黄佩琪，徐 琪，叶 丹，孙 媛，栾奎峰，刘世杰，2，童小华，2

（1.同济大学 测绘与地理信息学院，上海 200092；2.上海市航天测绘遥感与空间探测重点实验室，上海 200092；3.上海海洋大学 海洋科学学院，上海 201306）

1 引言

激光测高卫星由于速度快、精度高、节省人力物力［1］等优势，成为了当今获取大范围地表三维信息的重要工具之一［2］。此外，星载激光雷达具有穿透性强、精度高的优点，其产品同时还可以服务于生物量估算［3］、海冰厚度测算、海底地形测量［4-5］等领域。ICESat-2（Ice，Cloud and Land Elevation Satellite-2）于2018 年9 月发射［6］，搭 载全新激光测高系统ATLAS（Advanced Topographic Laser Altimeter System）。上一代卫星ICESat 于2003 年1 月发射升空，2010 年2 月停止工作［7］。相较ICESat，ICESat-2 搭载的激光测高系统利用微脉冲多波束光子计数激光雷达技术［8］对地进行观测，且有着更小的足印与更高的重复频率［9］，同时改用6 波束（强弱波束两两组合）的观测方式，增强了坡度适应性和测量精度。得益于单光子探测技术的应用，ICESat-2 卫星的探测器寿命将会有所延长［10］。

由于单光子探测器自身的高灵敏度［11］，接收回波时，背景噪声、探测器自身噪声等会随信号涌入探测器［12-13］。单光子探测技术能够在一定程度上减少噪声对结果数据精度的影响，但残余噪声仍会干扰数据的使用，故想要获得高精度的测高数据，还需要用点云滤波算法对噪声进行进一步的剔除。

本文首先选取了144 组具有代表性的光子点云数据，分析了不同地表覆盖类型（城市、沙漠、冰盖/冰川、海洋、植被及海冰）在不同季度、不同观测时间（白天/极昼、夜晚/极夜）下背景光子率的分布特点，之后对7 种具有代表性的光子点云滤波算法的实现思路及去噪过程进行总结。

2 ICESat-2 背景光子率分析

数据的背景噪声大小在很大程度上影响了点云滤波的去噪效果，本节首先对不同地表覆盖、不同观测条件下所获取ATLAS 的ATL03 数据（包含测量光子的经纬度、飞行速度等信息的ICESat-2 测高数据）的背景光子率进行了统计分析。

2.1 背景光子率

背景光子率表示点云数据中背景噪声光子数占总光子数的比率。在ICESat-2 描述光子地理位置的ATL03 数据中，6 个通道组（gt1l、gt1r、gt2l、gt2r、gt3l、gt3r）均包含一个描述背景噪声信息的组——bckgrd_atlas，其中包含一个bckgrd_rate 数据集，记录了剔除可能的信号光子后，发射50 次激光所得到测高直方图中的背景光子率，单位为点/秒。

2.2 实验数据

为探究不同地表覆盖类型、不同观测条件下背景光子率的分布特点，实验选取了6 种地表覆盖类型，四个季度白天和夜晚（海冰数据为极昼和极夜）共144 组数据（城市、沙漠、冰盖/冰川、海洋、植被及海冰各24 组）进行背景光子率的统计。为确保所选数据的代表性，实验针对每种地表覆盖类型各选取了三个实验区域，分布情况为城市类型选取北京、休斯顿和伦敦区域；沙漠类型选取塔里木盆地、撒哈拉沙漠和维多利亚大沙漠区域；冰盖/冰川类型选取青藏高原、格陵兰岛和南极洲冰盖区域；海洋类型选取海南省南部沿海、美国东海岸和几内亚湾区域；植被类型选取岭南、西伯利亚和亚马逊丛林区域；海冰类型选取南极洲沿海、北冰洋、俄罗斯北部沿海区域。

2.3 实验结果

为保证所选取范围内的地表覆盖类型尽可能单一，本文分别对上述144 组测高数据进行了1 秒和2 秒的数据截取，并对背景光子率进行了统计。由于两个截取时长下的背景光子率统计结果相近，因此下文统计结果与分析均使用截取时长为2 秒的测高数据。实验统计了所有数据在2 秒内的背景光子率总均值、同一地表覆盖类型下不同研究区域间和不同季度间的背景光子率相对标准差，以及强弱波束的背景光子率均值，结果如图1 所示。其中，横坐标上下的柱形图分别表示六种地表覆盖类型数据在白天（海冰数据为极昼）和夜晚（海冰数据为极夜）的背景光子率均值，黑色短线表示不同季度间的相对标准差，红色短线表示不同研究区域间的相对标准差。红色方块和蓝色菱形分别表示弱波束和强波束记录下的背景光子率均值。为方便表达，后文中未加以特别说明时，海冰数据的“极昼”和“极夜”均以“白天”和“夜晚”表示。

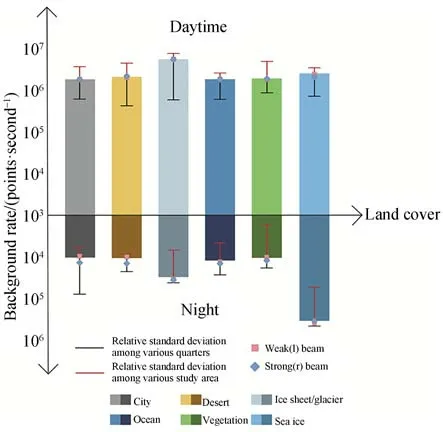
图1 不同地表类型背景光子率统计Fig.1 Statistics of background rate of different land cover

2.4 实验结论

通过对上述统计结果的分析，可得结论如下：

（1）对于除海冰外的其余五种地表覆盖类型（城市、沙漠、海洋、冰盖/冰川及植被），ICESat-2所获取的测高数据背景光子率在白天平均为106点/秒数量级，夜晚平均为104点/秒数量级。海冰数据在极昼期间，背景光子率平均为106点/秒数量级，极夜期间平均为105点/秒数量级。

（2）除海冰数据，冰盖/冰川数据的年平均背景光子率在白天和夜晚均为最高，分别为6.330 6×106点/秒 和3.298 2×104点/秒。总 体上看，背景光子率受被测物体自身反射率的影响，反射物质较为单一的地表覆盖类型（冰盖/冰川、海洋、沙漠、海冰）测高数据的背景光子率略高于反射物质较复杂的地表覆盖类型（城市、植被）的背景光子率。

（3）根据相对标准差的统计可得，所选数据具有代表性，除城市夜晚和冰盖/冰川白天的数据，其它测高数据的背景光子率在四个季度间均无明显差异；除植被夜晚和海冰夜晚的数据，其它测高数据的背景光子率在不同区域间也无明显差异。

（4）强弱波束间背景光子率在数量级上无明显差异，由此可见波束能量的强弱仅体现在信号光子的数量差异，而非背景光子率的不同。

此外，为研究2 秒内背景光子率变化情况，本实验还对比分析了背景光子率随时间的变化情况。如图2 所示，其中，黄线为白天弱波束数据，红线为白天强波束数据，蓝线为夜晚弱波束数据，紫线为夜晚强波束数据。结论如下：

图2 背景光子率变化对比Fig.2 Comparison of background rate changes

（1）除海冰数据，其余地表覆盖类型数据的背景光子率在夜晚的变化均比白天情况更复杂，波动幅度更大。

（2）被测物体表面反射率越高、反射物质越单一的地表覆盖类型，背景光子率曲线更平稳。例如，在同一季度的数据中，城市区域（反射物质不单一）比沙漠区域（反射物质单一）的背景光子率曲线变化更复杂，如图2（c）和（d）所示；平坦沙漠区域（表面反射率较低）比平坦冰盖/冰川区域（反射率较高）的背景光子率曲线变化更复杂，如图2（e）和（f）所示。

（3）地面坡度变化越大的数据背景光子率变化幅度越大，例如研究区域1（青藏高原）冰川数据比研究区域2（格陵兰岛）冰盖数据的背景光子率变化更大，如图2（g）和（h）所示。

（4）在实验统计的大多数测高数据中，白天强弱波束的背景光子率曲线之间在时间尺度上均会出现一定程度上的偏移，尤其在植被及城市类型的部分数据里偏移明显。这是由于强弱波束在沿轨方向上存在一定间隔，因此，同组数据中一对强弱波束所记录的信息会在时间上有一定的偏移。植被和城市类型的地表反射物体相对于其他四类地表覆盖类型更为复杂，故该偏移也更为明显。

3 ICESat-2 滤波算法研究进展

从上节分析可得，夜晚背景光子率要远低于白天，这意味着夜晚获取的数据精度要高于白天。同样地，由于不同类型的地表覆盖对光子有着不同的反射率，不同类型的光子点云数据也呈现了不一样的特点。然而，通常情况下，测高数据中，被探测物体表面的光子密度远大于噪声光子密度。据此，学者们开发出了多种光子点云滤波算法，大致可分为3 类［14］。（1）栅格化滤波法：将点云数据进行栅格化，使其转化为二维图像，而后利用数字图像处理算法（如Canny 边缘检测［15］、轮廓检测［16］等）对栅格化后的数据进行处理，剔除噪声。这类算法思路简单且处理效率高，但栅格化操作会导致一定程度的数据损失［17］，难以精细化去噪。（2）局部统计量法：计算点云数据中每个光子点的局部统计量（如光子与周围k个最邻近光子的距离和），并对该量进行直方图统计，根据直方图设定阈值对噪声进行剔除［18］。局部统计量法并未导致数据损失，且能够反应信号和噪声的分布密度差，但该算法效果依赖阈值选取，且手动选择阈值的过程会导致算法自适应性的降低。（3）密度聚类分析法：遍历光子数据，依据密度将光子点云分为噪声光子和信号光子［19］。聚类分析的方法较为灵活，也更好地利用了点云剖面图中噪声和信号的密度差，但该类方法的结果受点云分布及搜索区形状的影响，故选择合适的搜索区对于获得好的聚类结果至关重要。

为研究不同类型算法的去噪效果及探究噪声数量对去噪效果的影响，在本文第2 节分析结论的基础上，从144 组实验数据中选取了21 组具有代表性的数据，然后从现有的点云滤波算法中，选取7 种典型算法进行去噪思路总结并对该21 组测高数据分别进行去噪处理，分析去噪精度并总结不同算法的特点。根据处理思路的特点，可将该7 种点云滤波算法分为前述三个大类，如图3 所示。

3.1 栅格化滤波法

栅格化滤波法将光子点云剖面图分为若干个栅格，利用每个栅格单元中的统计量（如栅格内的光子数等）将栅格转化为二维图像，使用数字图像处理算法进行去噪。

栅格化滤波法中，较有代表性的直方图统计法 由Brunt 等 在2014 年［20］提 出。首先使用固 定大小的窗口将光子点云剖面图进行分块，统计每个窗口中的光子总数，接着利用光子总数的统计量进行阈值的选取，从而达到信号窗口和噪声窗口的划分。算法实现的具体步骤可分为5 步：（1）统计光子数；（2）信号窗口初筛选；（3）识别遗漏信号窗口；（4）创建信号光子缓冲区；（5）创建高程中位数缓冲区。

直方图统计法处理效率高，但也有着栅格化滤波法的弊端，数据被压缩、细节受损，因此后续的滤波算法多以单个光子为最小单位。

3.2 局部统计量法

局部统计量法以单个光子为计算单元，避免了数据丢失、忽略细节的问题。局部统计量法首先计算点云中所有点的局部统计量，接着生成局部统计量的直方图，根据直方图选择合适的阈值，从而将每个点识别为噪声光子或信号光子。

3.2.1 局部距离和法

夏少波等于2014 年［21］提出使用局部距离和法对光子点云剖面进行信号的提取，通过逐一计算剖面图中光子到周围最邻近k个点的距离和作为局部距离，结合直方图统计来寻找分割噪声和信号的阈值。算法过程可概括为3 个步骤：（1）计算局部距离和；（2）直方图统计；（3）设定阈值剔除噪声。

3.2.2 密度维度法

密度维度法（Density-dimension Algorithm，DDA）由Herzfeld 等于2017 年［22］提出，该算法提出将光子密度作为一个新的维度，利用径向基函数来计算每个光子周边指定范围的局部密度，以此作为局部统计量来分割噪声和信号。具体计算步骤为：（1）分割点云为噪声块和信号块；（2）利用径向基函数计算局部光子密度；（3）计算双重阈值剔除阈值。

局部统计量法对于地形的适应性较高，同时也不会造成数据的丢失，能够处理数据的细节部分，所以去噪效果相比栅格化滤波法有了很大的提高

3.3 密度聚类分析法

密度聚类分析法大多不需要手动确定阈值，在确定搜索区的大小和形状后，对点云剖面中的每个光子进行遍历，加以判断处理即可将信号点聚为一类，从而完成去噪。

3.3.1 概率比较法

2016 年，Wang 等［23］提 出一种利用贝叶斯概率公式辅助去噪的自适应算法。该算法利用光子周围最邻近k点的距离与贝叶斯概率公式计算光子作为噪声和信号的概率，二者比较后得出光子分类结果。

3.3.2 改进DBSCAN 法

DBSCAN（Density Based Spatial Clustering of Applications with Noise）法为计算机视觉中典型 的聚类 算法之 一，Zhang 等在 2014 年［24］针对ICESat-2 数据的分布特点，提出了一种改进的DBSCAN 算法。与常规的DBSCAN 算法不同，由于被测地物的光子以水平分布为主，所以该算法将搜索区的形状由常规的圆形改为了以水平方向为长轴的椭圆形，算法对水平分布的点更敏感，相近的分布密度下，算法更容易将水平方向的点聚为一类。

3.3.3 最佳滤波核法

谢峰等于2014 年［25］提出了一种利用方向可调的滤波核进行去噪的算法。在改进DBSCAN法中，椭圆形搜索区的横轴是保持水平不变的，而最佳滤波核法则是通过旋转滤波核的主轴来寻找其最佳方向，再利用不同方向加权平均的方法提高算法对最佳滤波核方向信号光子的提取能力。

3.3.4 改进局部密度法

改进局部密度法由Zhu 等在2018 年［26］提出，该算法利用了局部方向最大点密度和直方图曲线拟合来提高去噪算法的精度。近似研究还包括改进OPTICS 法［27］、四叉树法［28］等。

相较于前两类点云滤波算法，密度聚类分析法对于先验知识、参数的依赖性更低，因而对于不同分布类型的点云数据适应性更高，但对于数据和搜索区的要求也较高。

3.4 去噪实验数据

本文去噪实验所采用的数据如表1 所示。

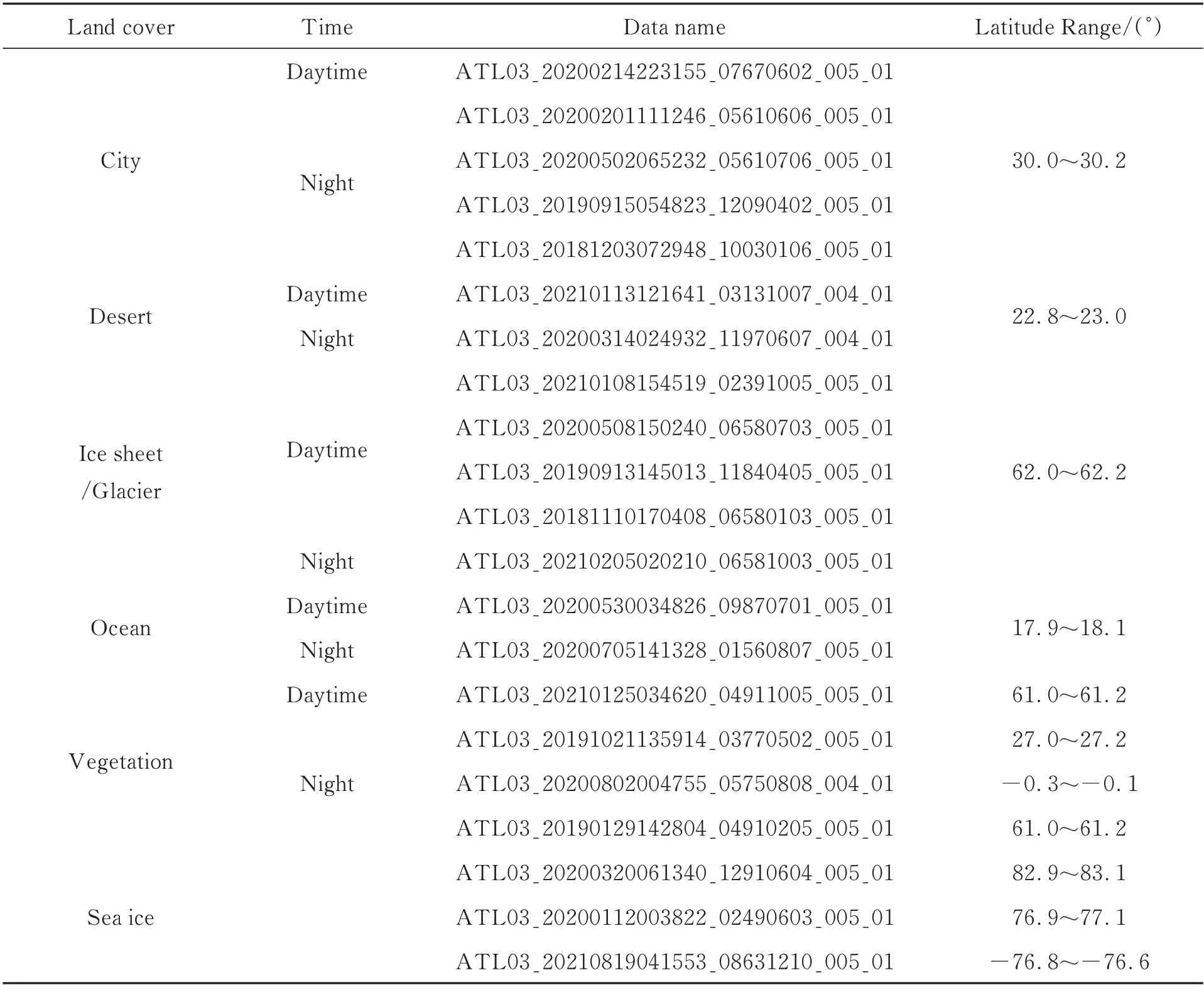
表1 去噪实验数据信息Tab.1 Informations of the data in denoising experiment

3.5 去噪实验结果

利用7 种具有代表性的滤波算法对上述21 组数据进行去噪处理后，采用召回率（Recall）、精准度（Precision）及F值进行精度评估。精度计算所采用的标准数据是在ALT03 数据标签的基础上，结合研究区域遥感影像，对测高点云数据进行目视解译得到的测高点云数据。

首先，对不同算法的三个精度指标进行了统计，如表2 所示。

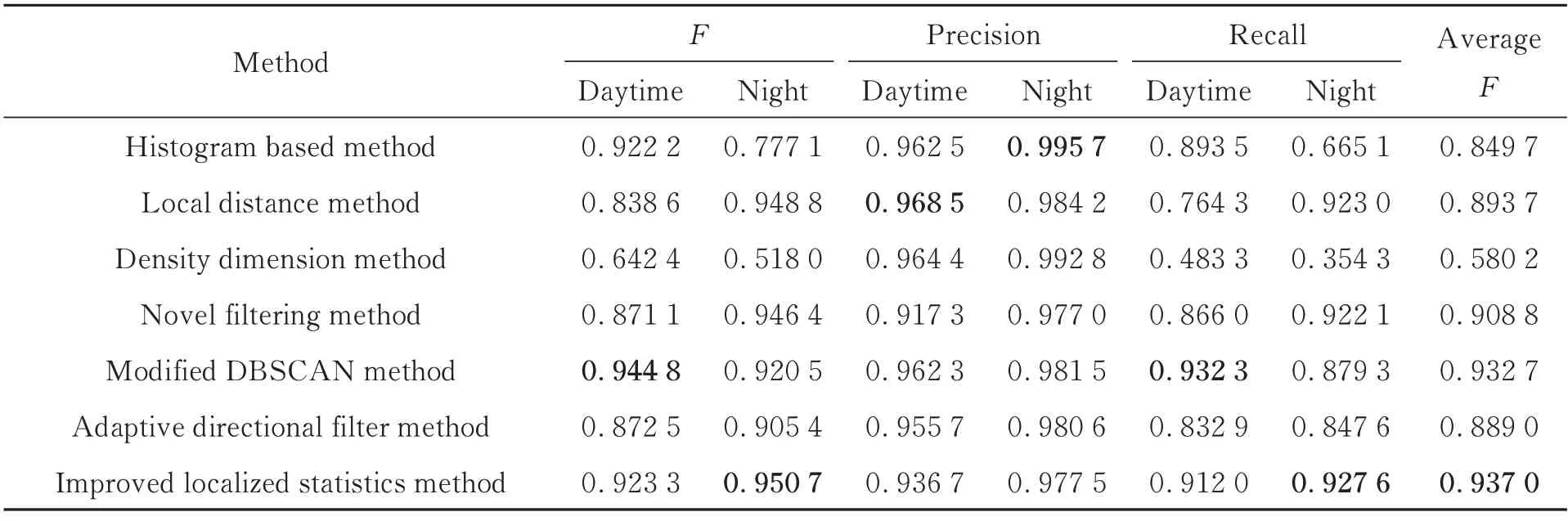
表2 不同滤波算法精度Tab.2 Accuracy of different filtering algorithms

为直观展示各地表类型的去噪效果，选取对应效果最好的滤波算法进行展示，结果如图4 所示，其中红色为信号光子，黑色为噪声光子。

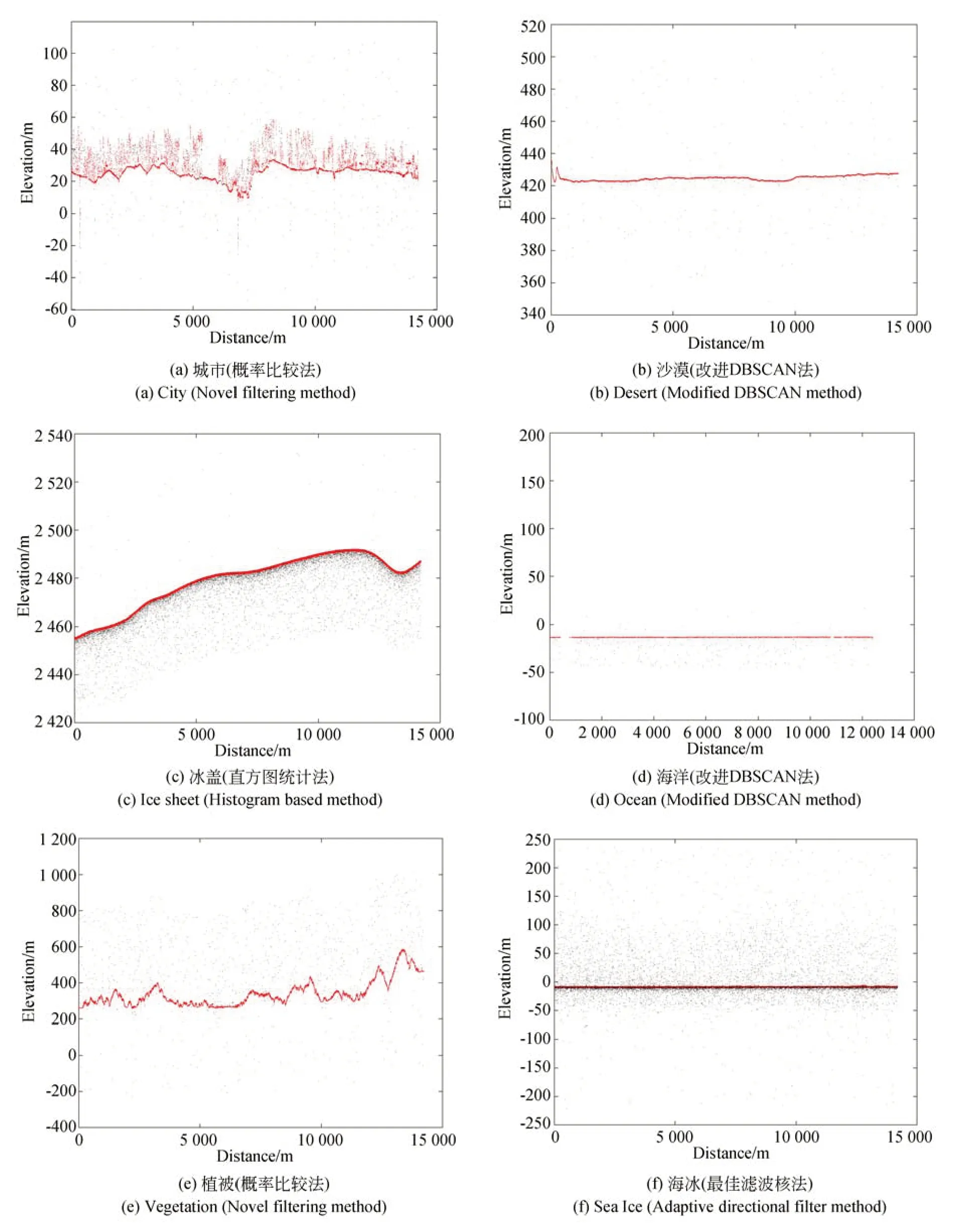
图4 各地表覆盖类型数据去噪结果Fig.4 Denoising results of different land cover

由统计结果可见，不同算法间的精准度相差不大，均达到了0.91 以上，但召回率相差较大，最高的改进局部密度法达到了0.927 6，而最低的密度维度法仅有0.354 3；而F值同时衡量了精准度和召回率，因此从F值可以得出改进局部密度法去噪效果最好，密度维度法效果欠佳。

对于不同观测条件，夜晚数据去噪结果的精准率均远高于白天数据的去噪结果；在召回率和F值方面，直方图统计法、密度维度法、改进DBSCAN 法对白天数据的去噪处理效果优于夜晚数据的去噪效果，局部距离和法、概率比较法、最佳滤波核法和改进局部密度法对夜晚数据的去噪效果优于对白天数据的去噪效果。上节统计结果显示，夜晚数据的背景光子率远低于白天数据的背景光子率，二者结合说明总体上看，噪声数量对于去噪效果的影响较小。

精准度计算的是在滤波结果中，筛选出的信号光子中有多少是真正的信号光子。统计结果说明，背景光子率越小，噪声光子对信号光子的影响越小，在分离噪声和信号光子时，噪声更不容易与光子混淆，因此夜晚数据去噪结果的精准度比白天更高。

实验还对不同地表覆盖类型在所有算法处理下的总均值进行了统计，如图5 所示。可以看到，冰盖/冰川数据去噪效果最好，海洋数据去噪效果最差。总体上看反射面成分更单一、地形起伏更小的数据（沙漠、冰盖/冰川、海冰）去噪效果优于地表覆盖较为复杂、地形起伏较大的数据（城市、植被）。海洋数据总体去噪效果差，经观察是由于在去噪实验所选的白天数据中，反射表面的信号光子与背景噪声光子密度较接近，基于信噪光子密度差研发的滤波算法无法较好地提取出海洋信号光子，因此拉低了昼夜平均的去噪精度。

图5 各地表类型去噪结果统计Fig.5 Statistics of the denoising results of various land cover

实验还计算了21 组数据的背景光子率及上述三个指标的相关系数，结果发现整体去噪效果和背景噪声之间的相关性并不是很高。

实际上，在进行去噪实验的过程中我们发现，噪声的分布情况对去噪效果的影响大于噪声的数量对去噪效果的影响。例如城市和植被同属于地形起伏和地表覆盖复杂、地表反射率较低的类型，但植被数据存在大量近地表的噪声光子，总体上看，滤波算法对植被数据的去噪效果比对城市数据的去噪效果差，因此可以说明，噪声的分布对于去噪的效果有一定的影响。

此外，为探究不同算法对于不同地形的适应性，实验还分别统计了7 种算法对于不同地形起伏数据的去噪效果差异。最后得出：7 种算法中，坡度适应性最差的是直方图统计法，相对地，改进局部密度法坡度适应性最好。

4 ICESat-2 滤波算法特点分析

从实验结果可以得到，首先，背景光子率的统计实验结果显示，白天数据的背景光子率远高于夜晚数据的背景光子率，但昼夜数据去噪的平均F值相近，分别为0.859 3 和0.852 4，且在实验采用的七种算法中，直方图统计法、密度维度法、改进DBSCAN 法对于白天数据的处理总精度高于夜晚数据，说明背景光子率对ICESat-2 测高数据的总精度影响不大。实验结果还显示所有算法对白天数据去噪精准度均小于夜晚数据，白天平均精准度为0.952 5，而夜晚为0.984 2，这说明背景光子率的大小主要影响去噪精准度，背景光子率越大，精准度越低，被错分为信号的噪声越多。其次，影响去噪效果的因素除背景噪声数量外，还有噪声的分布及信号本身的特性，接近信号光子的噪声信号越多（如近地表的地下光子）、噪声密度与信号密度越接近、地表起伏越大、覆盖物越复杂，去噪效果越差。最后，不同算法对噪声的敏感程度以及对坡度的适应性均有不同。总体上看，改进局部密度法的去噪精度最高，对噪声的敏感度更低，效果也更为稳定。

结合去噪过程中出现的问题及精度计算结果，表3 对算法是否需要输入参数、适用地表覆盖类型、算法特点进行总结。

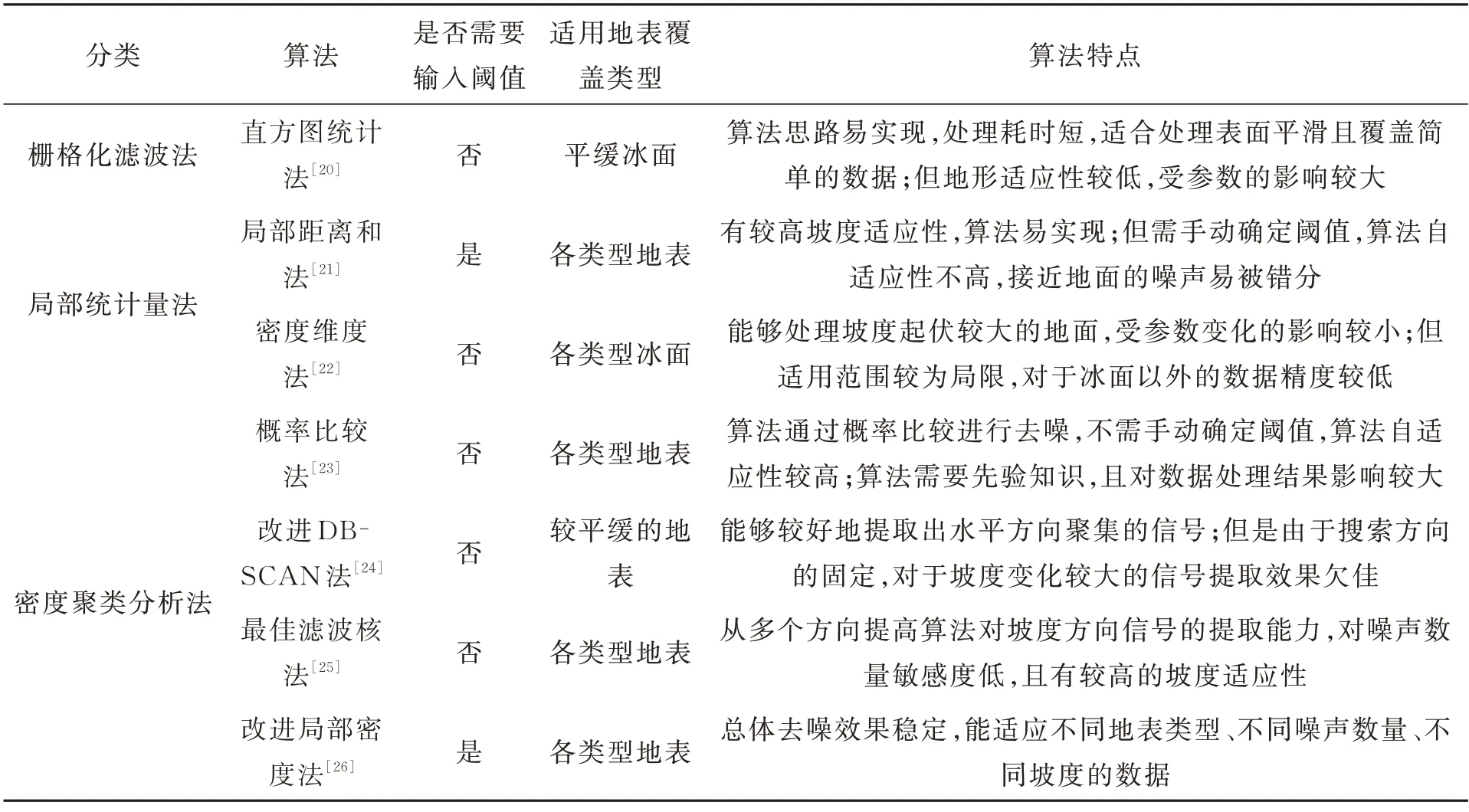
表3 点云滤波算法总结Tab.3 Summary of photon filtering algorithms

直方图统计法对数据进行了压缩，提高了处理速度，但无法处理点云剖面图细节，适合处理地表起伏小、反射率高、地表覆盖简单的数据；局部距离和法效果较好，但在信号光子分布密度不均时，生成的直方图会出现多个波峰，阈值选取会影响信号的保留情况；密度维度法采用了更为严格的双重阈值，所提取的信号会比真实信号数量少，但准确度高，适用于地表覆盖单一且光子分布集中的地形，如各种地形的冰面；概率比较法对先验信息的要求较高，先验参数的细微偏差会对去噪结果精度产生较大的影响；改进DBSCAN 法对水平方向信号的提取能力有所提高，但固定的搜索区方向使得该算法在处理坡度较大的数据时，所提取的信号会出现断续的现象，适用于处理平缓、密度分布较均匀的数据；最佳滤波核法经过粗去噪和精去噪的过程，利用方向可变的滤波核及加权平均密度，大大提高了坡度适应性，实验验证该算法精度处于较高的水平；改进局部密度法对局部光子密度方向进行了搜索，该操作提高了算法的坡度适应性，同时利用两个高斯函数对密度直方图进行了拟合，提高了算法应对不同地表覆盖类型数据的去噪能力。

5 结论

本文首先统计分析了不同地表覆盖类型测高数据背景光子率的分布特点，得出以下结论：光子点云测高数据的背景光子率在白天约为106点/秒数量级，夜晚约为104点/秒数量级；反射率较高、反射面组成更单一的地表覆盖类型背景光子率更高，背景光子率的变化幅度越小；强弱波束所记录的背景光子率在数量上相差很小。

然后，本文对不同地表覆盖类型数据使用7种具有代表性的滤波算法进行了处理，分析得到背景光子率的密度对去噪效果的影响低于背景噪声光子分布（密集程度和被测地形）对去噪效果的影响；直方图统计法处理效率最高，但效果欠佳，适合处理较简单平缓的测高数据；改进DBSCAN 法、最佳滤波核法和改进局部密度法去噪效果较好，其中，改进局部密度法的去噪效果最佳，算法召回率、精准度和F值平均分别为0.919 8、0.957 1 和0.937 0，效果较为稳定。

而针对光子点云滤波算法的不足之处，本文总结了以下几点想法：

（1）由点云滤波算法的发展可知，如今一些算法正是利用了计算机视觉的处理算法来对点云进行去噪（如改进DBSCAN 法和改进OPTICS 法），该类算法有着较高的自适应性，所以可以进一步将点云去噪算法与计算机视觉、深度学习等领域相结合，提高算法的精度和自适应性；

（2）由于同一阈值作用于不同的坡度可能会获得不同的去噪效果，所以针对坡度变化较大的数据可以采用分段阈值的方法，在不同坡度的数据段使用不同的阈值，以提高算法对坡度的适应性；

（3）在测高数据中，接近地面的区域会存在一些分布密度与信号光子分布密度相近的噪声点，因此有些算法无法将此类噪声点剔除，这会对后续的地面提取及高程估计等步骤产生一定的影响。可以考虑使用迭代或者多重阈值的方式，利用二次筛选将误判成信号的地面噪声点剔除。