基于动态空腔膨胀模型的土壤Mohr-Coulomb参数反演方法

邹 欧，薛 健，李 娜，王 鑫，杨 荣，李玉琼*

（1.中国科学院大学 工程科学学院，北京 100049；2.中国科学院 力学研究所 流固耦合系统力学重点实验室，北京 100190；3.中国科学院 力学研究所 非线性力学国家重点实验室，北京 100190）

1 引言

土壤强度参数解译在定量评估军事装备机动性和指导装备轻量化结构设计等方面具有重要作用，在地质勘测、装备全域机动、地外行星科考等重大需求领域中有广泛的应用背景［1-5］。传统“取样-室内实验”是典型的非原位测试方法，取样造成的土体扰动——特别是原位应力的解除——使得所采集试样的力学性质不能真实反映土壤原本的力学特征，从而影响对土壤承载性能及装备车辆通行性的可靠评估［6］。因此，基于现场原位贯入触探测试并结合相关理论实现土壤原位力学参数的精准、快速反演的需求日益紧迫。目前，土壤原位贯入测试方法主要有静力触探（Cone Penetration Test，CPT）和自由落体贯入触探。静力触探能获得土壤强度参数随深度的变化情况，一般需要外载荷持续作用以保持匀速贯入（2.5 cm/s），设备安装耗时长，操作费用高［7-8］，难以满足复杂地质环境和大范围区域内土壤力学参数的测量，限制了其在装备机动性评估方面的应用。自由落体贯入触探技术是在静力触探基础上发展起来的一种新型原位测试技术，它依靠自由落体贯入仪（Free Fall Penetrometer，FFP）以一定初始速度贯入土壤，通过传感器实时记录贯入过程中贯入仪的加速度和受到的阻力，来反演土壤强度参数。FFP 结构轻便、操作简单且较为经济，能够实现复杂环境和较大区域内土壤强度参数的快速测量［7，9］。

目前，在海洋工程中，已有相关研究利用FFP 获取土壤强度参数。Aubeny 等人［10］提供了基于数值模拟建立的不排水抗剪强度计算方法，给出了承载力系数的经验公式；Stoll 等人［11］通过对贯入实验所得数据进行最小二乘拟合，得到了贯入阻力和最大减速度之间的关系。研究表明贯入过程中的阻力可表示为一个与贯入速度有关的阻力函数［12-14］。通过确定土壤强度参数与阻力函数之间的关系，结合贯入仪上传感器记录的加速度数据可反演土壤强度参数。True［15］给出了一个描述FFP 贯入海床土过程的半经验阻力函数，其中考虑了端部阻力、侧壁摩擦阻力、土壤拖曳阻力以及土体浮力的作用。Chow 等人［9］利用离心机实验中传感器测量的加速度数据，反演了饱和软黏土的不排水抗剪强度，并考虑了率效应对软黏土强度的影响。刘君等人［16］采用数值仿真的方法模拟了贯入仪在软黏土中的运动，研究其所受阻力与贯入速度、土壤强度和界面摩擦系数之间的关系，提出了一种反演软黏土不排水抗剪强度的方法。以上反演方法均基于True 提出的半经验阻力函数，其中包括承载力系数，界面摩擦系数，拖曳阻力系数等许多经验参数，当缺少场地土壤条件前期资料时，经验参数取值会对反演方法的准确性产生重要影响。此外，以上方法仅能针对海洋工程中常见饱和软黏土的不排水抗剪强度进行反演。这表明，由于实际地质环境的复杂性，基于自由落体贯入技术的冲击贯入机理还有待更深入的研究，参数反演方法还需完善，其适用性还需拓展。

在贯入阻力的理论研究方面，现有方法主要包括承载力理论［17］，应变路径理论［18］和空腔膨胀理论［19-26］。承载力理论仅考虑土体破坏区域的整体平衡，而破坏区域内各点并不处于平衡状态。Janbu 等人［27］通过黏性土的静力触探实验表明，利用承载力理论求得的贯入阻力相比于实测值低约40%。应变路径法只能近似求解饱和黏性土的情况［18］，对于砂土，由于贯入时的流场难以构造，该方法并不适用。

空腔膨胀理论是研究侵彻问题的重要模型。由于FFP 的刚度远大于土壤，在贯入过程中变形较小，因此FFP 贯入土壤的过程可视作刚性弹侵彻靶体的过程。若将贯入仪看作由一系列与其内切的球形空腔组成，则贯入仪与土体之间的相互作用就可看作这些球形空腔在无限大介质中均匀膨胀时与土体介质间的相互挤压［28］。通过求解介质中空腔膨胀的径向应力分布，就可得到弹体贯入过程中受到的贯入阻力。Bishop［19］首先给出了准静态柱/球形空腔膨胀理论的控制方程，并利用它求解了尖锥体对金属靶的压入阻力问题。Chadwick［20］将这个理论应用到理想土壤材料，结合Mohr-Coulomb 屈服准则，得到了土壤径向位移的表达式。Cao 等人［21］假定土的本构为修正剑桥模型，通过求解准静态空腔膨胀理论控制方程，得到了土体内的超孔隙水压力和总应力。Hill［22］则首先给出动态空腔膨胀理论控制方程，得到了不可压缩理想弹塑性靶体对弹体的阻力。基于动态空腔膨胀理论，Forrestal 等［23-25］开展了针对于不同靶体材料（如岩石、混凝土及土壤等）的侵彻研究，大大拓宽了这一理论的应用范围。Shi 等人［26］针对干砂的冲击贯入，建立了考虑压缩性的动态空腔膨胀理论。动态空腔膨胀模型准确地刻画了稳定贯入过程中贯入阻力和贯入速度平方间的线性关系，展现了清晰的物理图像，而土壤强度参数则反映在阻力系数当中，这为土壤强度参数反演提供了理论基础。

本文基于冲击贯入触探技术和动态空腔膨胀模型，开展了土壤Mohr-Coulomb 参数（内聚力和内摩擦角）反演方法的研究。利用土壤冲击贯入实验中测得的阻力-速度曲线、加速度时程曲线、速度时程曲线以及贯入深度-初速度关系，对贯入阻力系数进行了拟合，进而对Mohr-Coulomb 参数进行了反演。最后，对参数可解域和参数敏感性进行了讨论。

2 动态球形空腔膨胀模型

一般来讲，在对土壤的冲击贯入过程中，贯入仪可视作刚体。此时，动态球形空腔膨胀模型为计算弹-靶相互作用提供了一个简单的物理图像。这个模型将贯入仪看作是由一系列与其内切的球形空腔组成，空腔球心在贯入仪的对称轴上［28］。贯入仪与土体的相互作用可看作是这些球形空腔在无限大介质中均匀膨胀时与土体介质间的相互挤压。这样一来，贯入仪侧表面上每一点的法向应力可近似为球形空腔膨胀时内表面的径向应力，它与空腔膨胀的速度有关，而空腔膨胀速度为贯入仪侧表面上该点的法向速度分量［25，28］。由于球对称性的引入，经过以上简化后，贯入仪侧表面上的压力分布就可转化为一个一维问题进行求解。贯入仪图示及球形空腔膨胀模型如图1。

球形空腔的膨胀将导致土体介质出现相应的动态响应，形成弹塑性分区［25］（如图1（b））。记空腔膨胀速度为V、弹塑性边界扩张速度为c、初始时刻空腔的半径为零，则在t时刻塑性区的范围为（Vt，ct），弹性区的范围为（ct，+∞）。在弹性区内，土壤的本构关系采用Hooke 定律来描述，并且假定弹性区内土壤不可压缩。在塑性区内，采用体积锁定的假设［25］来描述土壤的应力应变关系，即发生塑性变形后土壤的体积应变为常数η*，不随平均应力的增大而变化。在这个假定下，静水压力将不影响土壤的后继屈服。记ρ0和ρ*分别是土壤的初始密度和锁定密度，则：

图1 贯入仪及球形空腔膨胀模型Fig.1 Penetrometer and spherical cavity expansion model

土壤的屈服准则采用Mohr-Coulomb 准则，在球坐标系下可写为［25］：

其中：σr，σθ分别为径向应力和环向应力（以压为正）；p=（σr+2σθ）/3 为平均应力；τ0，λ是与土壤内聚力C和内摩擦角φ有关的常数，且有［29］：

冲击贯入过程中，质量、动量及能量守恒定律均需得到满足。对于贯入阻力和贯入深度的解答，仅利用质量守恒和动量守恒关系即可得到。在球坐标系下，拉格朗日坐标表示的质量守恒方程和动量守恒方程可写为：

其中：r是拉格朗日坐标，u为径向位移（以向外为正）。空腔表面处的边界条件为：

弹塑性界面处的Hugoniot 条件可表示为［24］：

其中，v是介质的径向速度，下标1、2 分别代表弹塑性界面处的弹性区和塑性区。

利用以上本构关系和边界条件求解控制方程（4）和（5）可解析地得到贯入仪端部表面的法向应力分布为［25］：

其中：Vz是贯入仪在竖直方向的速度；A，B是与τ0/E，λ和η*有关的参数。根据λ的不同取值，A，B的表达式存在如下三种不同的情况［25］：

式（12）中的第2 式表明，在贯入过程中空腔膨胀速度V与弹塑性边界扩张速度c的比值始终保持为常数。随着贯入深度的增加，贯入速度减小，空腔膨胀速度V也逐渐减小，对应的弹塑性区域的扩张逐渐变慢。

对于贯入仪相对土壤垂直贯入的情况，将式（9）在贯入仪端部积分，则得到贯入仪所受到的竖直方向阻力Fz为［25］

其中：

αs和βs是与土壤力学特性有关的系数。其中ψ=s/（2r）是贯入仪头部的曲径比，并且有θ0=arcsin［（2ψ-1）/（2ψ）］（见图1（a））；μ为贯入仪与土壤间的滑动摩擦系数，二者之间的切应力可表示为στ=μσn。如果忽略贯入仪与土体间的摩擦（μ=0），并令：

式（18）和式（19）可进一步简化为：

由式（9）和式（17）可以看到，在当前模型假设下，贯入仪端部的应力分布及贯入阻力由两部分贡献，一项是静阻力项，另一项是流动阻力项（即速度平方项），而黏性效应和附加质量效应［14］未被考虑。

贯入仪在竖直方向的贯入速度Vz可由牛顿第二定律计算得到，注意到式（17），有：

其中，m为贯入仪的质量。积分上式即得到：

其中，V0=Vz（t=0）是贯入仪的初始贯入速度。贯入过程中贯入仪加速度大小为：

最终贯入深度P为：

3 土壤Mohr-Coulomb 参数的反演

3.1 Mohr-Coulomb 参数C，φ的反演方法

土壤Mohr-Coulomb 参数即土壤的内聚力C和内摩擦角φ。由于动态空腔膨胀模型刻画了土壤力学特性参数对弹靶相互作用的影响，因此对C和φ的反演可以建立在动态空腔膨胀模型的基础上。由式（3）可知：

上式表明，要反演内聚力C和内摩擦角φ，实际上就是要求得参数τ0和λ的值。由式（18）、式（19）（或对于不考虑摩擦时的方程（21）和（22））以及A、B的表达式可见，参数τ0、λ包含在阻力系数αs、βs中。一旦 求得αs和βs，联立方 程（18）和（19）（或对于不考虑摩擦的情况，联立方程（21）和（22）），即可求得参数τ0和λ的值。

在联立方程（18）和（19）（或方程（21）和（22））求解参数τ0和λ时，需针对A、B取值的三种情况进行讨论。由于参数A、B的表达式过于复杂，一般不能得到τ0和λ的解析表达式。此时，可采用如下几何化方法进行求解。为简便起见，忽略掉贯入仪与土体间的摩擦（即令μ=0），不影响对方法的讨论。

（1）如果λ≠0 且λ≠3/4：

此时，由式（10）和式（11）可见，参数A、B均为（τ0，λ）的函数。根据式（21）和式（22），αs、βs也均是（τ0，λ）的函数。因此，由式（21）和式（22）可定义如下曲面：

此种情况下若存在τ0和λ的解，那么参数τ0和λ必是曲面Π1和Π2的公共零点。

（2）如果λ=3/4 或λ=0：

此时，由式（13）～式（16）可见，参数A、B仅是τ0的函数。因此αs、βs也仅是τ0的函数。于是，根据式（21）和式（22）可定义如下曲线：

此种情况下若存在τ0的解，则τ0必是曲线L1和L2的公共零点。

至此，对C、φ的反演就归结为对阻力系数αs和βs的计算，它们可通过贯入阻力、贯入速度、贯入加速度以及最终贯入深度的测量结果计算得到。下面就针对这些情况进行具体说明。

3.2 基于阻力-速度关系进行的反演

在冲击贯入过程中，最重要的物理量是贯入仪受到的贯入阻力Fz，它综合反映了靶体介质的物理力学性质以及贯入仪与靶体材料之间的相互作用。动态空腔膨胀模型的核心就是揭示了贯入过程中的稳定阶段贯入阻力Fz（t）与速度平方间的线性关系（式（17））。因此，我们首先利用这个关系来反演土壤的Mohr-Coulomb参数。

实际当中，贯入阻力Fz（t）可由加速度传感器测量得到；而贯入速度Vz（t）则可由加速度时程曲线积分得出。因此，利用测量数据集｛Fz，i，Vz，i｝并基于式（17）进行线性拟合，即可得到参数αs和βs的数值，并进而求得内聚力C和内摩擦角φ。为此，构造误差函数：

其 中，N是数据采样点数目。得 到αs，βs的数值后，即可按照上节所述步骤进行C，φ值的反演。下面采用Forrestal 等人［25］报道的实验结果来对这个反演方法进行详细说明。

文献［25］中，通过对不同采样地点取样的土壤进行三轴压缩及单轴压缩标定实验，测得的土壤参数如表1 所示。需要说明的是采样地点和现场贯入实验地点的土层按照深度可分为三层［25］，第一层（Ⅰ：0～1.8 m）的弹性模量为120 MPa，锁定体积应变为0.17；第二层（Ⅱ：1.8～3.0 m）的弹性模量为150 MPa，锁定体积应变为0.10；第三层（Ⅲ：3.0～6.1 m）的弹性模量为210 MPa，锁定体积应变为0.13。为了简化模型计算，文献［25］忽略了土壤的分层，将其视作均匀介质，并取三层土壤的平均弹性模量（160 MPa）和平均锁定体积应变（0.13）作为土壤基本参数。本文按照同样的假定进行计算。

表1 Forrestal 实验土壤参数［25］Tab.1 Soil parameters of Forrestal′s experiments［25］

以文献［25］中的贯入实验3 为例，贯入仪质量为23.1 kg，弹体半径r=47.6 mm，弹头曲径比ψ=3。忽略贯入过程中贯入仪与土体间的摩擦。由实验测得的加速度数据计算得到贯入阻力和贯入速度后，给出的阻力-速度平方关系如图2 所示。由图2 可见，除初始阶段贯入仪与土体碰撞造成的震荡以及贯入结束阶段的土体扰动外，在中间的稳定贯入阶段，贯入阻力与贯入速度的平方之间呈线性关系，这表明动态空腔膨胀模型揭示了贯入过程的关键特征。根据式（17），对稳定贯入阶段的阻力-速度关系进行线性拟合，结果如图2 中红线所示，拟合得到的阻力系数为αs=85.39 kN，βs=2.52 kg/m。图中A、B两点分别是拟合范围的起点和终点，黑色圆点是参与拟合的数据。关于拟合范围的选取，将在第4.2 节中进行详细讨论。

图2 贯入阻力Fz和贯入速度平方Vz2间的关系［25］Fig.2 Relationship between penetration resistanceFzand penetration speed squareVz2［25］

由拟合得到的阻力系数αs、βs，可按照式（28）和式（29）画出曲面Π1和Π2的图像，如图3。由图3（a）、图3（b）可见，曲面Π1与坐标平面Π1=0 有交线l1（曲面Π1零点的集合）；曲面Π2与坐标平面Π2=0 有交线l2（曲面Π2零点的集合）。将交线l1和l2画在同一坐标系下，如图4 所示，可见二者有公共交点（τ0=5.52 MPa、λ=0.58），显然，这个交点就是曲面Π1和Π2的公共零点。按照第3.1节的分析，此时的τ0和λ就是所要求的解。此外，对于λ=3/4 和λ=0 的情况也应当进行校验。按照式（30）和式（31）分别画出曲线L1和L2的图像（如图5（a）和图5（b）所示），可以看到，对于这两种情况，L1和L2都没有公共零点，因此不存在τ0和λ的解。综合以上分析，将τ0=5.52 MPa 和λ=0.58 代入式（27），就得到C、φ的反演结果分别为：

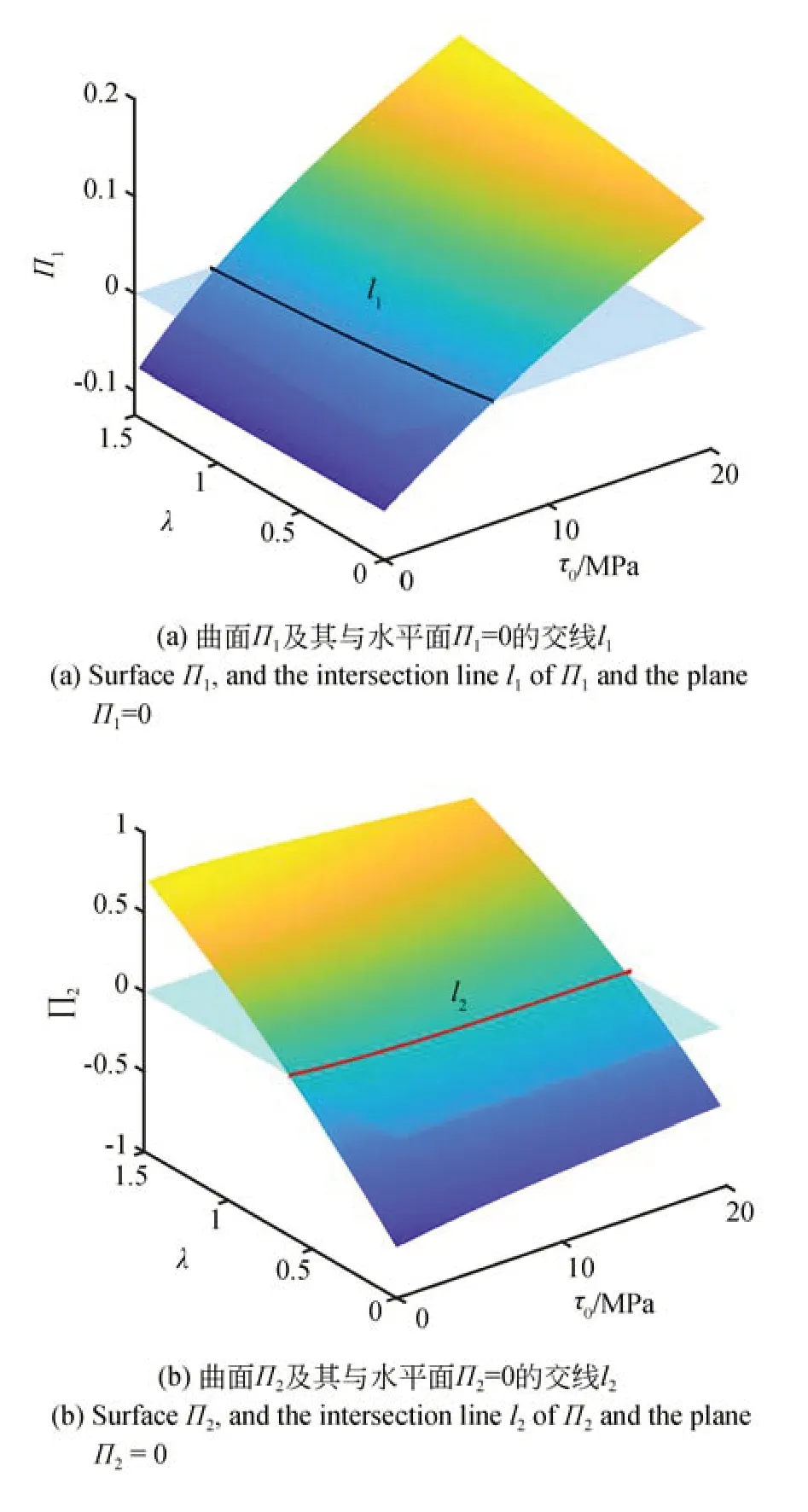
图3 曲面Π1和Π2的图像Fig.3 Images of surfacesΠ1andΠ2

图4 λ≠0 且λ≠3/4 时交线l1和l2的图像及其交点Fig.4 Intersection linesl1andl2and their intersection point underλ≠0 andλ≠3/4

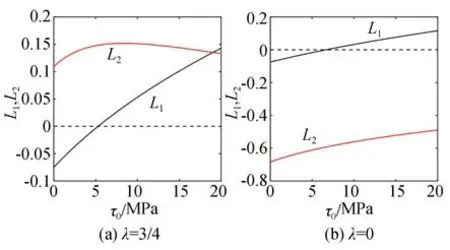
图5 λ=3/4 或λ=0 时曲线L1、L2的图像Fig.5 LinesL1andL2whenλ=3/4 orλ=0

对于实验中的土壤试样，Forrestal 等人［25］给出了三轴实验下剪切强度τ与平均应力p之间的关系，如图6，此处，剪切强度τ定义为试样屈服时第一主应力σ1与第三主应力σ3的差［25］（τ=σ1-σ3）。注意到空腔膨胀模型的球对称性，第一主应力σ1就是空腔膨胀时的径向应力σr，第三主应力σ3就是空腔膨胀时的环向应力σθ（此时σ2=σ3=σθ），于是Mohr-Coulomb 准则（式（2））可以写为：

根据上式，对图6 中的数据进行线性拟合（如图6 中红线所示），可解得相应的C、φ值分别为C=3.73 MPa、φ=3.48°。

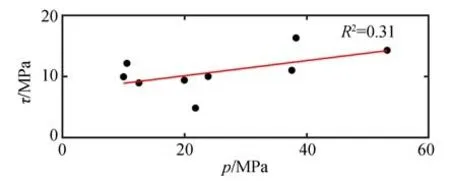
图6 剪切强度与平均应力的关系［25］Fig.6 Relationship between shear strength and average stress［25］

对比式（36）所示的反演结果可见，对于内聚力C的反演结果与三轴实验的结果较为接近，而对内摩擦角φ的反演结果却与实验值差别较大。这一定程度上与采用的拟合方法有关。接下来，我们分别基于贯入加速度数据和贯入速度数据对阻力系数进行拟合，并进一步讨论拟合结果对方法的依赖。

3.3 基于加速度时程曲线和速度时程曲线进行的反演

贯入加速度与贯入阻力间仅相差m倍，原则上讲，由贯入加速度进行阻力系数αs、βs的拟合与采用贯入阻力进行拟合没有本质差别。但是，在利用阻力-速度关系进行拟合时，贯入速度是由加速度的数值积分获得，由于进行了数值积分操作，数据处理过程与直接利用加速度时程曲线进行拟合是不同的，因此拟合结果也将产生差别。此外，由式（17）可见，贯入阻力Fz与贯入速度的平方Vz2间呈线性关系，阻力系数αs和βs通过线性最小二乘拟合即可得到；而由式（25）可见，贯入加速度az与时间t呈现非线性关系，αs和βs只能通过非线性最小二乘拟合得到。

基于加速度时程曲线［25］和速度时程曲线对阻力系数的拟合如图7。根据贯入加速度表达式（25），采 用Levenberg-Marquardt 方法［30］对文 献［25］中贯入实验3 给出的加速度数据进行非线性最小二乘拟合，如图7（a）中红线所示。拟合的初值设置为根据阻力-速度关系拟合得到的数值，即αs=85.39 kN，βs=2.52 kg/m。由加速度曲线拟合得到的阻力系数分别为αs=89.22 kN、βs=2.69 kg/m。由此得到τ0=5.61 MPa、λ=0.72，Mohr-Coulomb 参数为：

图7 基于加速度时程曲线［25］和速度时程曲线对阻力系数的拟合Fig.7 Fitting of the resistance coefficients based on acceleration and velocity curves

与三轴实验测量值相比，C值的相对误差为29.2%，与上一节中基于阻力-速度关系反演得到的结果接近，φ值的反演误差仍然较大。此外，图7（a）给出了按照文献［25］中取τ0=10 MPa、λ=0 时计算得到的加速度时程曲线（图7（a）中蓝线），将其与红线相比较可以看到，τ0=10 MPa 和λ=0 并不是测量数据的最小二乘解。

按照相同的非线性最小二乘拟合方法，利用贯入速度表达式（24）亦可对阻力系数αs和βs进行拟合，如图7（b）所示。此时，同样将拟合的初值设置为根据阻力-速度关系拟合得到的数值，即αs=85.39 kN，βs=2.52 kg/m。由速度曲线拟合得到的阻力系数为αs=101.48 kN、βs=1.87 kg/m。相应的τ0=7.76 MPa、λ=0.11，Mohr-Coulomb参数为：

将上式与三轴实验测量结果对比，C值的相对误差为2.14%，较前两种方法的反演结果误差大大减小，φ值的相对误差也减小为9.77%。

总结起来，对比式（36）、式（38）和式（39）的反演结果可见，利用阻力-速度关系进行拟合的结果与利用加速度直接进行拟合的结果相近，而与利用贯入速度进行拟合的结果差别较大。更重要的是，相较于前两者的拟合结果，利用贯入速度拟合得到的内聚力C和内摩擦角φ与三轴实验给出的结果更加接近。以上结论并不是偶然的，它反映了贯入阻力系数对加速度、速度等物理量有不同的影响，这将在第4.2 节中进行更进一步的讨论。此外，以上结论为土壤Mohr-Coulomb 参数反演方法的实际应用提供了重要参照。

3.4 基于深度-初速度关系进行的反演

阻力系数αs、βs的数值还可以通过对同一状态的土壤进行多次贯入实验后测得的贯入深度P和初始贯入速度V0来拟合。为此，根据式（26）构造误差函数：

其中，N是贯入实验次数。

可解得：

将式（44）代入式（43）并令：

实验中，弹体质量为286 g，弹头长度为140 mm，曲径比ψ=8.54［31-32］。土壤的基本参数如表2 所示。

表2 何翔实验的土壤参数［31］Tab.2 Soil parameters of He Xiang’s experiments［31］

表3 中列出了同一刚性弹以不同初速度多次贯入同一状态土壤后测得的贯入深度结果。图8为的图像及贯入深度-贯入初速度关系。将表3 中的9 个实验数据代入式（45）可画出函数f的图像（图8（a）），并得到的零点为1.09×10-3s2/m2，联立式（41）和式（44）可解得αs=276.92 N，βs=0.30 kg/m。取锁定体积应变η*=0.13，可得到τ0=52.51 kPa，λ=1.16，Mohr-Coulomb 参数为：

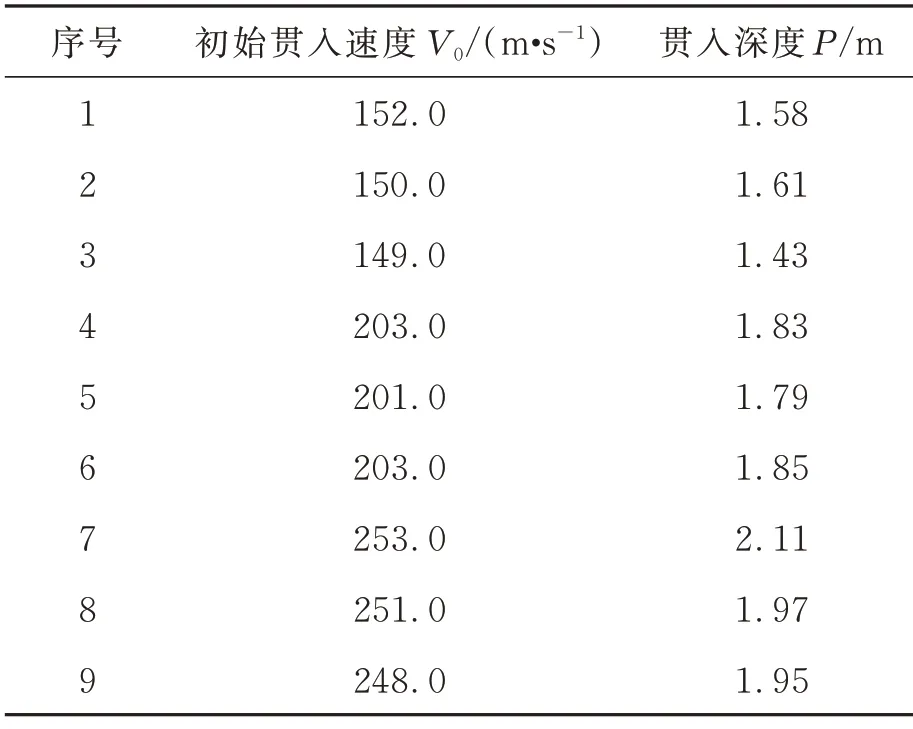
表3 何翔贯入实验结果［31］Tab.3 Results of He Xiang’s penetration experiments［31］

图8 的图像及贯入深度-贯入初速度关系Fig.8 Image of the functionand the relationship between penetration depth and initial speed

反演得到的内聚力C的相对误差为58.74%，内摩擦角φ的相对误差为3.07%。可见，利用9 个实验数据整体拟合反演得到的内聚力C与三轴实验测量结果相差较大，而得到的内摩擦角φ与三轴实验测量结果一致。

此外，对表3中所列数据进行分组拟合。根据文献［31］，表3 中所列实验结果对应三种不同的贯入初速度V0，分别为150 m/s（序号1～3），200 m/s（序号4～6）和250 m/s（序号7～9），在每个速度等级下取1 个数据点，总计3 个数据点作为一组数据（总共27 组），来拟合αs、βs的值，结果见表4。分组拟合及反演得到的内聚力C的平均值及标准差为29.45±20.69 kPa，内摩擦角φ的平均值及标准差为25.00±17.88°。此时，分组拟合并反演得到的C的平均值较整体拟合结果有所提高，但相比61 kPa 仍差别较大；而对于φ的反演，整体拟合结果与实验测得的30°更加接近。

表4 27 组数据的计算结果Tab.4 Calculation results of the 27 data sets

以上分析表明，利用贯入深度-初速度关系进行反演时，内摩擦角φ的反演结果更加可靠。

4 讨论

4.1 参数的可解域

土 壤Mohr-Coulomb 参 数C、φ并 不是任意的，具有一定范围，相应的阻力系数αs和βs也对应了一定范围，称为参数的可解域。只有拟合得到的αs和βs落在可解域范围内，才能在动态空腔膨胀模型框架下进行C、φ值的反演。

图9（a）和 图9（b）分别给出了Forrestal［25］和何翔［31］等人报道的实验结果对应的参数可解域。图9（a）中给出了利用阻力-速度关系、加速度时程曲线和速度时程曲线拟合得到的αs、βs值，其均落在参数的可解域内。图9（b）中的分组拟合值为第3.4 节中利用贯入深度-初速度关系对27 组数据拟合得到的αs、βs值；整体拟合值为利用9 个实验数据拟合得到的αs、βs值。这些拟合结果也都在参数的可解域内，因此可以利用动态空腔膨胀理论来进行C、φ值的反演。

图9 动态空腔膨胀模型下参数的可解域Fig.9 Solution domain determined by dynamic cavity expansion model

实际的地质环境往往十分复杂，数据噪声也难以避免，根据测量数据拟合得到的αs和βs并不总能反演得到Mohr-Coulomb 参数C、φ的数值。此时，就需要对偏离模型的过程进行更细致的分析

参数的可解域是土壤Mohr-Coulomb 参数对阻力系数作出的限制，它反映了土壤物理力学特性对贯入阻力的影响。对于给定土壤，Mohr-Coulomb 参数总是确定的，因此在理想情况下，阻力系数的实验值必定落在可解域内。但在实际当中，由于噪声的影响，或简化的模型未能涵盖贯入过程的复杂细节，阻力系数的拟合值可能超出参数的可解域。此时，就需要对冲击贯入的物理过程进行更加详细的分析，并对相应的数据处理手段进行优化。

4.2 拟合区间的选取及对反演结果的进一步讨论

由第3 节的分析可以知道，要准确地反演C、φ的数值，关键是要准确地拟合阻力系数αs和βs。第3.1 节至3.3 节利用贯入时程曲线进行拟合时，拟合数据是稳定贯入阶段贯入阻力与贯入速度平方呈线性关系的部分（图2 中A、B之间的数据）。数据拟合范围对阻力系数的拟合及Mohr-Coulomb 参数的反演有重要影响，在这一节中就来对数据拟合范围的选取进行讨论。

为此选取拟合窗口起点为图2 中的点A（对应时刻为t=4.84 ms），改变拟合窗口终点tend进行阻力系数αs和βs的拟合以及Mohr-Coulomb 参数的反演，结果如图10 所示。由图可见，不论拟合窗口的大小如何改变，基于阻力-速度关系反演的结果与基于加速度曲线反演的结果接近，而与基于速度曲线的反演有较大的差别；并且，对于内摩擦角φ，前两者的反演结果始终大于后者。

图10（a）显示了两个关键拟合范围。第一个范围对应三条拟合曲线的交点（tend=t2）。对于内聚力C的反演，当tend＜t2时，基于阻力-速度关系和加速度曲线反演得到的结果小于利用速度曲线反演的结果；当tend＞t2时，基于阻力-速度关系和加速度曲线反演得到的结果大于利用速度曲线反演的结果。在tend=t2的拟合范围下，三种拟合方法得到的C的反演结果一致。此时反演得到的数值（C=4 MPa）比三轴实验结果（C=3.73 MPa）大7.24%。另一个关键拟合范围对应于图10（a）中速度曲线拟合结果的最小值点tend=t1（这一点也是图10（b）中速度曲线拟合结果的最大值点），此时，由速度曲线拟合并反演得到的内聚力C=3.81 MPa，内摩擦角为φ=3.14°，与三轴试验结果一致。这一范围就是在第3.1 节至3.3 节中拟合时所采用的范围，图10 中时刻tend=t1就对应图2 和图7 中的点B。

图10 拟合区间大小对C、φ反演结果的影响［25］Fig.10 Influence of the fitting interval on the inversion results ofCandφ［25］

以上分析为反演方法的实际应用提供了一个可行方案：对于冲击贯入实验测得的数据，用速度曲线进行参数C（φ）的拟合，改变区间的大小进行搜索，使得C（φ）的拟合值最小（大）时对应的区间即为最终的拟合区间，相应的C、φ值即为最终的反演结果。

由图2、7、10 可以看到，拟合区间终点tend一般并不能覆盖整个贯入过程的数据段，图10 中能够反演得到Mohr-Coulomb 参数的最大tend为27.80 ms，这是由于参数可解域的限制。当tend大于27.80 ms 后，拟合得到的αs和βs已经超出了参数的可解域，这表明超过27.80 ms 后的贯入过程可能存在模型忽略掉的细节。在利用动态空腔膨胀模型进行参数反演时，假定了土壤介质的初始状态是均匀的，这一假设保证了模型的球对称性，而在现场贯入实验中，土壤实际上是分层的。图11 给出了文献［25］中贯入实验3 的加速度时程曲线并根据贯入仪进入不同土层（Ⅰ、Ⅱ、Ⅲ）的时刻进行了划分。由第3.2 节的说明可知，这三层土壤的弹性模量和锁定体积应变是不同的，特别是第三层土壤的弹性模量明显高于前两层；此外，第三层土层的厚度也几乎是前两层的两倍，贯入仪大部分的运动时间在第三层土壤中。这表明，第三层土壤对贯入过程的贡献应当比前两层土壤的大，然而平均化的假定抹平了这些差别。当拟合区间为图11 中的AB范围时，贯入仪在三个土层中的运动时间相差不大，此时，平均化的假定基本适用；而当拟合区间范围逐渐扩大，比如对于AC段或AD段，此时第三个土层的贡献逐渐增大（但仍与前两层可比拟），平均化的假定将产生误差，此时可能需要考虑土壤分层的影响。总之，准确地反演土壤的力学参数，需要模型能够准确地把握贯入过程的关键细节。

图11 贯入过程的加速度时程曲线以及贯入仪进入不同土层对应的时间区间［25］Fig.11 Acceleration curve and the time interval corresponding to the penetration instrument entering different soil layers［25］

4.3 参数的敏感性

在求解冲击贯入问题时，对于贯入阻力和贯入深度的求解属于正问题。此时，弹性模量和锁定体积应变等参数对于计算结果的影响不大［25］。然而，对于通过测量贯入阻力求解靶体介质力学特性参数这样的反问题，反演结果往往具有参数敏感性。这种敏感性不仅与材料参数本身有关还与阻力系数有关。

图12 和图13 分别给出了文献［25］和文献［31］中，土壤弹性模量E和锁定体积应变η*对C、φ值反演的影响。由图可见，随着弹性模量E的增大，反演得到的C值减小、φ值增大；随着锁定体积应变η*的增大，反演得到的C、φ值均增大。

图12 利用速度曲线［25］进行反演时，参数E、η*对C、φ值反演的影响，其中αs=101.48 kN、βs=1.87 kg/mFig.12 Influence of parametersEandη* on the inversion results ofCandφ，respectively，whereαs=101.48 kN andβs=1.87 kg/m（using the velocity curve［25］）

由图12（a）和图13（a）可见，弹性模量E对于C、φ值反演结果的影响较小。在图12（a）中，当弹性模量E的变化范围为135 MPa 时，C值的变化大约仅有1 MPa，而φ值的变化约3°。在图13（a）中，当弹性模量E的变化范围为45 MPa 时，C值的变化不到2 kPa，而φ值的变化小于1°。这就是说，C、φ值的反演结果对弹性模量E不敏感。相反地，由图12（b）和图13（b）可见，锁定体积应变η*对于C、φ值的反演结果却有很大影响，即C、φ值的反演结果对参数η*是敏感的。

图13 利用贯入深度-初速度数据［31］进行反演时，参数E、η*对C、φ值反演的影响，其中αs=276.92 N、βs=0.30 kg/mFig.13 Influence of parametersEandη* on the inversion results ofCandφ，respectively，whereαs=276.92 N andβs=0.30 kg/m（using the penetration depth-initial velocity data［31］）

此外，从图12（b）和图13（b）还可以看到，不同阻力系数导致根据相同范围内的η*反演得到的C、φ值也不相同。这说明反演结果的参数敏感性也与阻力系数αs、βs有关。

5 结论

本文基于动态空腔膨胀模型，利用土壤冲击贯入实验中测得的阻力-速度关系、加速度时程曲线、速度时程曲线，以及贯入深度-初速度关系，建立了对土壤Mohr-Coulomb 参数（内聚力C和内摩擦角φ）进行反演的方法。其中，基于前三者建立的反演方法是利用单次贯入过程中的时程曲线进行的反演；而基于贯入深度-初速度关系建立的反演方法则是在对同一状态的土壤进行多次贯入时采用。

在贯入过程中的稳定贯入阶段，贯入阻力与贯入速度平方之间呈线性关系，准确地拟合线性系数（阻力系数）αs和βs是反演Mohr-Coulomb 参数的关键。本文揭示了利用动态空腔膨胀模型进行Mohr-Coulomb 参数反演时存在一个关于参数的可解域。对于测得的实验数据，只有首先保证拟合得到的阻力系数落在可解域范围内，C、φ值的反演才能在动态空腔膨胀模型的框架下进行。

本文分析表明利用阻力-速度关系进行反演的结果与利用加速度时程曲线进行反演的结果相近，而这两者与利用速度时程曲线进行反演的结果差别较大。这本质上是由于阻力系数αs、βs分别对加速度和速度的贡献不同。因此，这三种反演方法对C、φ值反演的准确性也是不同的。其中，利用速度时程曲线进行参数反演的结果最为准确。利用Forrestal 等人［25］报道的土壤原位贯入实验结果进行的方法验证表明，利用速度时程曲线对土壤内聚力反演的相对误差为2.14%，对土壤内摩擦角反演的相对误差为9.77%。

此外，Mohr-Coulomb 参数的反演具有参数敏感性，这不仅与材料参数本身有关还与阻力系数αs和βs有关。C、φ值的反演结果对锁定体积应变η*敏感，而对弹性模量E不敏感。

本文建立的反演方法可为复杂地质环境下土壤Mohr-Coulomb 参数的快速确定提供基础，并为大范围内的地质力学信息勘测提供一个新的途径。