超声速双轨火箭橇系统两级减振与分析
杨 珍,付 良,赵项伟,杨 阳
(中国兵器工业试验测试研究院,陕西 华阴 714200)
火箭橇沿钢轨高速运动的试验过程中,受到火箭发动机推力脉冲、轨道不平顺度、气动力、制动力等复杂激励载荷因素的影响,试验时的振动力学环境难以控制,在不采取任何减振措施的条件下,所能提供的冲击、振动环境条件较导弹制导与控制装置真实工作环境恶劣得多,随着试验速度的提升,火箭橇振动力学环境恶化程度加剧,直接针对火箭橇与被试品接口位置进行简单隔振方法已经无法满足被试品力学环境要求,导致某些导引头火箭橇试验无法顺利开展,如何减振、隔振成为火箭橇试验中不可忽视的问题[1-2]。
近年来,国内外技术人员开展了多种火箭橇减振方法的有益尝试。美国霍洛曼基地公开了一种柔性火箭橇的设计概念,通过在滑靴和梁间增加蝶形弹簧,梁与载荷安装舱间增加钢丝绳弹簧,以减少传递到橇体和试验件中的能量,理论目标是将被试品在3 048 m/s速度下的振动控制在3gRMS内[3],但该项减振措施由于其挠度问题而没有实施,后采用弹性泡沫对被试品进行隔振,并从结构设计上提高橇体动态稳定性,在最大速度426 m/s试验环境下将被试品振动能量减小了25倍[4]。国内技术人员针对导引头火箭橇试验开展了一些低速状态的减振方法研究。丁春全等[5]针对减振系统出现异常工作问题,对3种不同阻尼减振器的减振效果进行了分析,发现较大的振动强度会影响减振器的正常工作。谢波涛等[6]采用金属干摩擦减振器构建了亚声速双轨火箭橇减振平台,成功将惯性测量装置的振动均方根控制在4g以内,但是由于减振器自身体积较大而未推广应用。解珍珍等[7]采用聚氨酯泡沫填充剂吸振和硅橡胶隔振方式降低导引头在超声速火箭橇试验过程中的振动,硅橡胶减振效果明显,但聚氨酯泡沫的竖向减振效果差。董治华等[8]建立了基础激励下双层减振模型,优化设计火箭橇减振系统,将被试品振动控制在5.6g以内。
上述研究对火箭橇的减振主要从载荷、结构设计和振动传递路径等方面进行减隔振,在速度较低的火箭橇试验中,取得了一定的效果,即在橇体各部件连接之间增加减振材料或元器件,将振源与被试品隔离,这种减振方法有效减小了被试品的振动量级。但是随着试验速度越来越高,火箭橇振动力学环境急剧恶化,这种单一减振方法的局限性愈发明显,极大地限制了火箭橇试验的发展。
本文结合前人研究经验,系统分析火箭橇激励源和振动特性。首先,从振源和振动传递路径出发,将天然橡胶与滑靴一体化融合设计为减振滑靴,减小滑靴刚度,从而减小由靴轨冲击碰撞引起的振动,实现火箭橇振源处的一级减振,并采用振动台试验和仿真方法对减振效果进行初步评估;然后,在被试品与橇体接口处采用硅橡胶隔振,从振动传递路径上实现被试品的二级减振;其次,对火箭橇系统进行运动学和动力学分析,评估其运动稳定性和结构安全性;最后,开展火箭橇试验验证,分析系统减振效果,提出进一步改进建议。
1 火箭橇系统振动特性分析
1.1 激励源及特性分析
引起火箭橇与轨道之间随机冲击振动的原因是火箭橇受到未通过其质心的发动机推力作用,沿不平顺轨道约束滑行,在气动载荷、靴轨冲击载荷等综合因素影响下,火箭橇激励载荷呈现出随机性、冲击性、幅值大且频带宽的特点。火箭橇系统的振动特性不仅与橇体结构、固体火箭发动机的结构、轨道系统的固有特性和几何状态有关,也与发动机推力载荷、火箭橇系统气动载荷和靴轨配合方式密切相关,滑靴与不平顺轨道的配合间隙是引起火箭橇和轨道耦合振动的主要因素[9-11]。
从载荷的时效性上将火箭橇的激励源分为瞬态激励和稳态激励。瞬态激励包括发动机点火与工作结束时的推力变化产生的瞬时大过载激励和轨道焊接接头对高速运动滑靴的冲击;稳态激励包括火箭滑车所受气动阻力、气动升力、滑轨不平顺与靴轨间隙引起火箭橇振动。
从火箭橇的振动频率来看,发动机瞬时大过载、脉动力及轨道焊接接头使火箭橇发生高频振动;火箭橇沿滑轨高速行驶时受到的发动机平稳推力、气动阻力和气动升力使橇体产生低频振动;轨道在建造和使用过程中引起的几何表面形位差异以及靴轨之间的间隙造成火箭橇在行驶过程中与轨道之间发生摩擦、碰撞和冲击力,这是一个宽频带激励。
1.2 刚性火箭橇振动特性分析
刚性火箭橇是指在试验过程中不采取任何减振措施的结构。振动测试数据是火箭橇系统在复杂激励源载荷作用下动态响应特性的直接体现。对多项未考虑减振措施的双轨火箭橇试验振动测试数据进行分析,得到了火箭橇体靴轨接触振源附近的振动加速度数据,发现火箭橇振动响应值与运行速度强相关,振动均方根值随速度的增加呈非线性增加趋势,且火箭橇刚度越大,振动响应越大。图1(a)为不同火箭橇在最大速度时刻的振动均方根值,从图中数据可以看出,当速度为900 m/s时,橇体上的振动响应均方根达到120g。图1(b)为某火箭橇在运动全程的振动功率谱密度曲线,由图中数据可知,火箭橇试验中产生的振动表现为随机振动,频带范围覆盖了5~2 000 Hz,且低频振动十分剧烈。

图1 刚性双轨火箭橇振动特性Fig.1 Vibration characteristic of rigid dual-rail rocket sled
2 火箭橇系统的两级减振设计
2.1 减振方法
本文从振源和振动的传递路径出发,设计两级减振平台,即在滑靴与橇体平台之间将减振材料与滑靴进行一体化设计为一级减振结构,使其满足滑靴承载要求的同时减小橇体振动;橇体平台与被试品接口之间设计二级减振,使其满足被试品安全固定要求的同时减小被试品振动,二级减振火箭橇如图2所示。

图2 两级双轨减振火箭橇Fig.2 Two-stage dual rail soft sled
2.2 减振设计
①减振滑靴设计与验证。
滑靴是火箭橇的关键构件,火箭橇借助环抱在滑轨轨头上的滑靴而沿着轨道高速运行,滑靴与轨道的轨头之间保持一定间隙,这使滑靴顺利通过具有几何不平顺的滑轨。正是这种带间隙的滑动配合方式,使得滑靴将火箭橇高速运行时在载荷作用下产生的冲击与振动传递到滑轨上;同时将滑靴与轨道之间因接触、摩擦和碰撞而产生的冲击与振动传递给火箭橇,靴轨接触力随航向速度增加而增加,马赫数为2时最大靴轨接触力为2.27×106N[12-14]。为使火箭橇安全平稳运行,传统的滑靴内部结构和连接结构均为刚性,其结构强度高、刚度大,火箭橇沿滑轨高速运行过程中,滑靴将振动冲击能量直接传递给了橇体其他部件,导致火箭橇系统整体振动水平高。因此,滑靴是振动的根源,要实现减振效果需在满足承载的条件下减小滑靴刚度。在有限的减振空间中,采用腔体结构将高强度滑靴与黏弹性材料进行一体化设计是减小滑靴刚度最为有效的方法。
减振滑靴由滑靴本体、减振材料和连接板三部分组成,滑靴本体下方为一体式滑块,与钢轨进行适配,本体上方设计有减振腔,腔内填充减振材料,考虑到滑靴的摩擦生热、金属黏合性、耐寒和加工性能,减振材料选用综合性能最好的天然橡胶[15]。滑靴的前后两端均设计有限位板和封板,用于对连接件、减振材料等进行限位。
②被试品减振设计。
硅橡胶在火箭橇试验中的减振效果已经通过振动台实验及火箭橇试验验证,能够有效改善圆柱形被试品的振动力学环境。本项目被试品固定段为圆柱形,因此直接采用硅橡胶进行二级减振设计。在被试品与卡环固定结构之间设计减振层,通过卡环下沉实现轴向限位,被试品前端悬空使其流场干净,在卡环上预留灌胶孔,在试验前进行灌胶并通过螺栓将孔洞封闭。
2.3 振动台试验验证
为检验减振滑靴设计的有效性,采用1∶1振动台扫频试验模拟滑靴受到激励后的振动响应特性,在滑靴不同位置布设加速度传感器,初步分析减振效果。根据橇体质量和滑靴数量对连接板配重,设置扫频范围10~2 000 Hz,激励信号从底座传递到滑靴底部,经橡胶减振后传递到连接板,减振前后振动响应曲线如图3所示,滑靴共振频率为228 Hz,367 Hz以上的高频信号得到了有效抑制。硅橡胶的减振设计为成熟技术,无需采用振动台试验来验证。

图3 减振滑靴振动台试验结果Fig.3 Test result of soft slipper on shaking table
3 动态响应分析
3.1 橡胶材料本构与参数确定
橡胶材料属于超弹性材料,其本构模型大致可以分为基于应变能函数的唯象模型和基于分子链网格的统计模型两大类。本文假定橡胶材料的变形为各向同性且均匀的,用Mooney-Rivlin模型来表示[16],其应变能密度函数模型为
(1)
式中:W为单位体积的应变势能;I1,I2为应变张量;C10,C01和D1为材料力学特性参数,由实验确定;J为弹性体积比,橡胶材料弹性体积模量极高,故J=1。将式(1)简化为
W=C10(I1-3)+C01(I2-3)
(2)
参数C10和C01通过单轴拉伸、等双轴拉伸、平面拉伸3种变形条件下的应力-应变关系测试拟合得到,拉伸试验中的应变水平为100%,拟合得到:C10=0.532×106,C01=-0.082×106。
3.2 减振滑靴动态响应分析
本文在有限元分析软件中建立减振滑靴实体模型,采用Mooney Rivlin不可压缩橡胶模型和双线性随动材料模型建立六面体减振滑靴有限元模型,如图4所示。产品橇共有4枚滑靴,仅对其中一枚滑靴按实际承载量配重进行模拟分析,将实测轨道不平顺数据作为位移激励载荷加载于火箭橇滑靴与轨道顶部接触面,通过显示动力学分析得到滑靴不同位置点的动态响应,如图5所示。在不平顺轨道载荷作用下,滑靴底部振动峰值达到约100g,而通过减振层后,振动峰值削减。
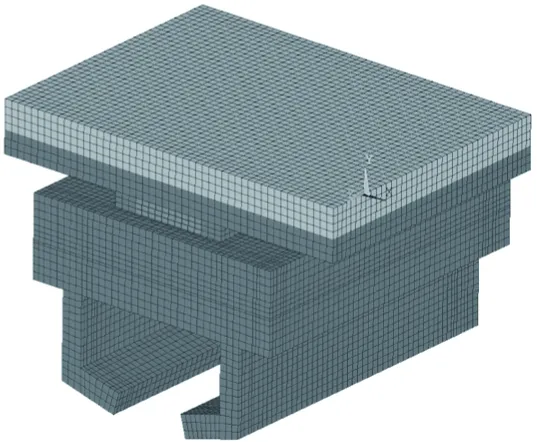
图4 减振滑靴仿真模型Fig.4 Simulation model of soft sled

图5 动态响应计算结果Fig.5 Dynamic response calculation results
3.3 橇轨耦合系统动响应分析
橇轨耦合系统动响应计算是对新型高速火箭橇平台进行运动稳定性和结构安全性快速分析的一种重要方法。火箭橇振动量与运行速度强相关,为快速检验新型火箭橇结构平台的运动稳定性和结构安全性,通常对火箭橇最大运行速度段进行橇-轨耦合动态响应分析,得到系统关键部件应力曲线及动态载荷[17]。
火箭橇系统由被试品、产品橇、一级橇和发动机构成,一级橇装载发动机推动整个系统按弹道曲线运动。将火箭橇和轨道系统进行工程简化,有限元模型中忽略承轨梁和基础等大质量结构,仅保留具有不平顺特性的钢轨,将钢轨的约束扣件结构简化为相应位置的位移约束,火箭橇与轨道之间采用滑动配合约束,建立的橇轨耦合系统模型如图6所示。

图6 橇轨耦合动力学计算模型Fig.6 Sled-rail coupling dynamics calculation model
由弹道曲线计算得到最大速度工况下的发动机推力,采用流体动力学软件计算得到火箭橇不同结构部件的气动力,将推力和气动力以载荷曲线方式施加到相应的结构部件,并给火箭橇一个初始运动速度。火箭橇在载荷作用下沿不平顺轨道滑行,不同的结构部件所产生的响应不同,通过计算,在最大速度条件下,火箭橇在滑轨上平稳运行,橇体各部件的动态应力都在材料强度极限内,被试品的侧向和竖向振动均方根值分别为13g和22g。
4 试验验证与数据分析
4.1 试验概况
自制模拟导引头作为被试品,设计最大速度700 m/s,产品橇安装减振滑靴,被试品与产品橇卡环之间灌注硅橡胶,在火箭橇前滑靴隔振层上、下位置各安装1枚振动传感器,导引头模拟件部位安装1枚振动传感器,共安装3枚传感器。火箭橇试验过程为发射点点燃助推火箭发动机,2 s时发动机工作结束达到最大速度后火箭橇系统减速滑行至轨道终点。火箭橇试验系统及测试点位布设情况如图7所示。

图7 火箭橇试验系统及测试点位布设示意图Fig.7 Schematic diagram of rocket sled test system and test location layout
4.2 振动数据分析
火箭橇试验顺利实施,并成功获取了振动数据,下面从振动均方根、功率谱密度两方面对3个点位前2 s加速段的振动数据进行对比分析,将数据以0.2 s为间隔进行分段,计算分段振动均方根值,如图8(a)和8(b)所示。火箭橇各部位的侧、竖向振动随速度的增加而增加,减振滑靴作为一级减振,其侧向减振效果优于竖向,因为轨道的侧向不平顺控制精度优于竖向,且双轨火箭橇稳定性好;当火箭橇运行速度大于440 m/s后,橇体的竖向减振作用明显,能够有效改善火箭橇的振动环境;硅橡胶减振作为二级减振,竖向减振效果明显,但侧向振动放大,被试品固定安装位置较高,固定结构刚度不足,导致振动放大;在马赫数为2的速度条件下,被试品侧向和竖向振动均方根均在12g以内,且随速度的增加缓慢变化。
火箭橇减振前后的侧、竖向功率谱密度如图8(c)和8(d)所示,通过滑靴和卡环部位的两级减振后,被试品实现了100~2 000 Hz宽频域减振。

图8 振动数据分析曲线Fig.8 Analysis curve of vibration data
4.3 减振效果分析
不同速度段减振效率如图9和图10所示。由图中结果可知,减振效率随速度增加而提高,后保持动态稳定,在马赫数为2的速度条件下,经过两级减振,竖向减振总效率约70%,侧向为52%。

图9 侧向减振效率Fig.9 Lateral vibration attenuation efficiency
5 结论
针对传统火箭橇在马赫数为2的速度条件下在轨力学环境超出导弹制导与控制元件许用范围问题,利用黏弹性材料的结构适应性优点,开展了两级双轨火箭橇减振设计,采用动态特性仿真、振动台试验初步验证了减振结构的有效性,通过橇轨耦合动力学分析评估了火箭橇系统的结构稳定性和安全性,并开展了火箭橇试验验证,对试验数据进行了分析,得到以下结论:
①采用腔体结构将滑靴与天然橡胶一体化融合设计为减振滑靴结构,可以有效减小从振源传递到橇体上的冲击振动值,火箭橇运行速度越高,减振效果越明显。
②在被试品和橇体接口部位采用硅橡胶材料可有效隔离橇体在竖直方向的振动,但连接刚度的减小以及被试品固定高度的增加导致其侧向振动放大。
③两级减振平台的成功研制使得双轨火箭橇实现了马赫数为2速度下的侧、竖向振动均方根小于12g的力学环境要求,能够为导引头、惯导装置火箭橇试验提供试验技术支撑。

