导弹飞行过程中动态载荷识别方法

张 浩,李新艳,黄 勇,王丙寅,陈国锋

(1.北京理工大学 宇航学院,北京 100081;2.南京理工大学 能源与动力工程学院,江苏 南京 210094;3.内蒙古动力机械研究所,内蒙古 呼和浩特 010010)

无论是在地面试车还是在自由飞行过程中,固体火箭发动机出现的不稳定燃烧往往都伴随着强烈的壳体振动,而弹体外部激励往往会引起导弹的结构振动,进而诱发发动机不稳定燃烧。因此,识别导弹的飞行动态载荷对于导弹结构设计和不稳定燃烧的预测与抑制具有十分重要的意义。而导弹飞行环境对应着复杂的载荷环境,这样的载荷环境往往会带来传感器难以安装,或者传感器的性能受到极大影响等问题,加之传感器设置本身也会对结构的正常运行甚至结构的动力学特性造成影响。因此,直接遥测外载荷是非常困难的。通过载荷识别方法来确定导弹在飞行过程中的动态载荷,具有很强的工程研究意义。

载荷识别属于结构动力学的第二类反问题[1]。时域内动态载荷识别的研究受众多学者的关注,DOYLE[2]采用小波反卷积的方法识别作用于板和梁结构的冲击载荷,识别载荷与实测载荷吻合良好。夏鹏等[3]提出了一种基于灵敏度分析的平稳随机动载荷分段时域识别分析技术,结果表明,灵敏度分析识别方法能够很好地识别出作用在结构上的随机动载荷,并具有良好的抗噪性。陈莲等[4]采用有限元仿真手段研究了动态载荷识别的计权加速度法。王彦卫等[5]利用函数来拟合系统响应,然后求解系统振动微分方程可得系统载荷。LIN[6]采用广义卡尔曼滤波器和递归最小二乘法建立了一种从一个非线性系统的实测动态响应数据中估计动态载荷的方法,并采用空气阻尼隔振器模型的数值仿真验证了所提方法的准确性。

相比而言,神经网络具有很强的非线性拟合能力,为解决导弹动态载荷识别提供了新的思路和方法。张方等[7]利用BP神经网络模型进行了动载荷识别的尝试,并通过仿真和实验证明了该方法的可行性。董会丽等[8]利用有限元仿真和RBF神经网络相结合的方式来辨识复合材料层合板壳结构的动载荷。随后一些学者利用神经网络对结构的周期性载荷或冲击载荷的载荷识别进行了实践,都取得了不错的成效。王珲玮[9]对飞行载荷参数识别的方法进行了研究,通过MIV算法筛选输入自变量,再通过BP网络训练模型,得到飞行载荷的识别结果。但对于工程结构特别是导弹这种处在复杂载荷环境中的结构所常常遇到的随机载荷,基于神经网络的载荷识别的研究开展得不多。本文设计并加工了一种导弹实验模型,开展地面试验,获取载荷数据和动态响应数据,结合BP神经网络进行了动态载荷识别研究。

1 导弹模态仿真与实验验证及神经网络的训练

1.1 有限元模型的建立

本文所使用的模型参照文献[10],并在其基础上进行简化,建模时忽略了对导弹整体模态影响不大的结构,如喷管内的非金属结构、吊挂等小零件。忽略了尾翼和前翼。建立的全箭被动段的几何模型如图1所示。网格划分为四面体网格,有限元模型如图2的全箭有限元模型所示。

图1 全箭被动段几何模型Fig.1 Geometric model of passive section of full rocket

图2 全箭有限元模型Fig.2 Full arrow finite element model

1.2 模态分析结果

本次仿真采用商业软件Ansys-Workbench计算全箭空载工况下的模态,并与模态实验结果进行比较,验证所用仿真模型的科学性和准确性。

仿真结果表明：该导弹模型一阶弯曲频率为36.499 Hz,二阶弯曲频率为80.711 Hz。振型如图3所示全箭空载一阶弯曲和图4所示的全箭空载二阶弯曲振型。

图3 全箭空载一阶弯曲振型Fig.3 No-load first-order bending vibration mode of whole rocket

图4 全箭空载二阶弯曲振型Fig.4 No-load second-order bending mode of whole rocket

1.3 模态实验

本文对所用实验模型进行模态试验,以验证仿真模型的准确性,实验系统结构示意图如图5的模态实验系统所示。

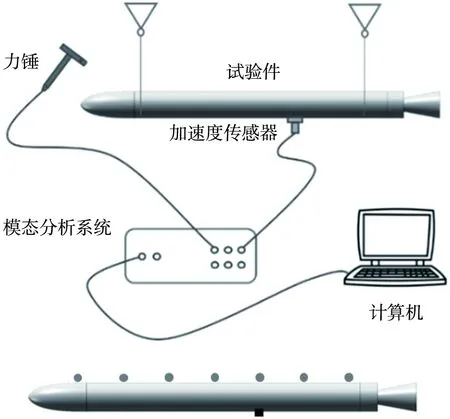
图5 模态实验系统及测点示意图Fig.5 Schematic diagram of modal experiment system and measurement point

模态实验所采用的实验方法为锤击法,测点位置如图5所示。黑色实心圆点为力锤敲击点,黑色方块为传感器安装位置。加速度计的粘贴位置保持不动,用力锤依次敲击测点。激励点、响应点位置均应避开箭体任一阶振型的节点,以此保证测点采集信号有较高的信噪比。实验过程中严格保证导弹纵轴呈水平,振动传感器应靠近主振动平面安装。

本文所使用仿真模型的第一、第二阶弯曲模态频率与实验测试结果对比见表1。由此可知,本文所用仿真模型与实验中所使用模型有较强的一致性,使用此模型开展后续工作训练神经网络具有科学性和可信性。

表1 模态频率对比Table 1 Modal frequency comparison

1.4 BP神经网络的训练

BP神经网络是一种多层前馈神经网络。BP神经网络结构包含3层：输入层、隐含层和输出层,如图6神经网络结构示意图所示。在实际应用中,往往依靠经验来确定网络的结构。文献[11]已经证明,BP神经网络有能力利用足够的神经元逼近非线性很强的函数。

图6 神经网络结构示意图Fig.6 Schematic diagram of the neural network structure

BP神经网络的设计主要包括网络层数选择、隐含层节点数设置以及网络传递函数的选择、训练方法的确定等。下面介绍这些要素的确定方法。

①网络层数的选择。

单隐含层的BP神经网络通过增加其节点数目已经能够逼近非线性很强的函数。经过实践,这里选用一个隐含层,即可满足需求。

②隐含层节点数目的设置。

隐含层节点数目对神经网络的识别精度甚至收敛性都有极大的影响。目前仍没有一套公认的算法来确定隐含层的节点数目,通常使用经验公式来估计该层的节点个数,本文使用的神经网络中隐含层的节点个数为15。

③传递函数的选择。

BP神经网络中的传递函数很多,这里选用最常用的Sigmoid函数。

④训练方法的确定。

除了最速下降法外,还有很多改进的方法。对于本文所用到的这种小型神经网络,LM算法收敛速度快,且学习过程中不会出现明显的振荡,所以选用LM算法作为训练方法。

图7为典型载荷加载示意图。基于Ansys-APDL平台,对有限元模型在如图7黑色实心圆点所示处(模型中间位置)沿法向施加典型载荷,得到加速度响应数据。以加速度数据作为输入数据,载荷数据作为输出数据,训练神经网络,共进行40种典型载荷的仿真分析,获取加速度数据。由于篇幅有限,这里仅列举几种最为典型的信号的波形,如图8所示。

图7 典型载荷加载示意图Fig.7 Waveform diagram of typical signal

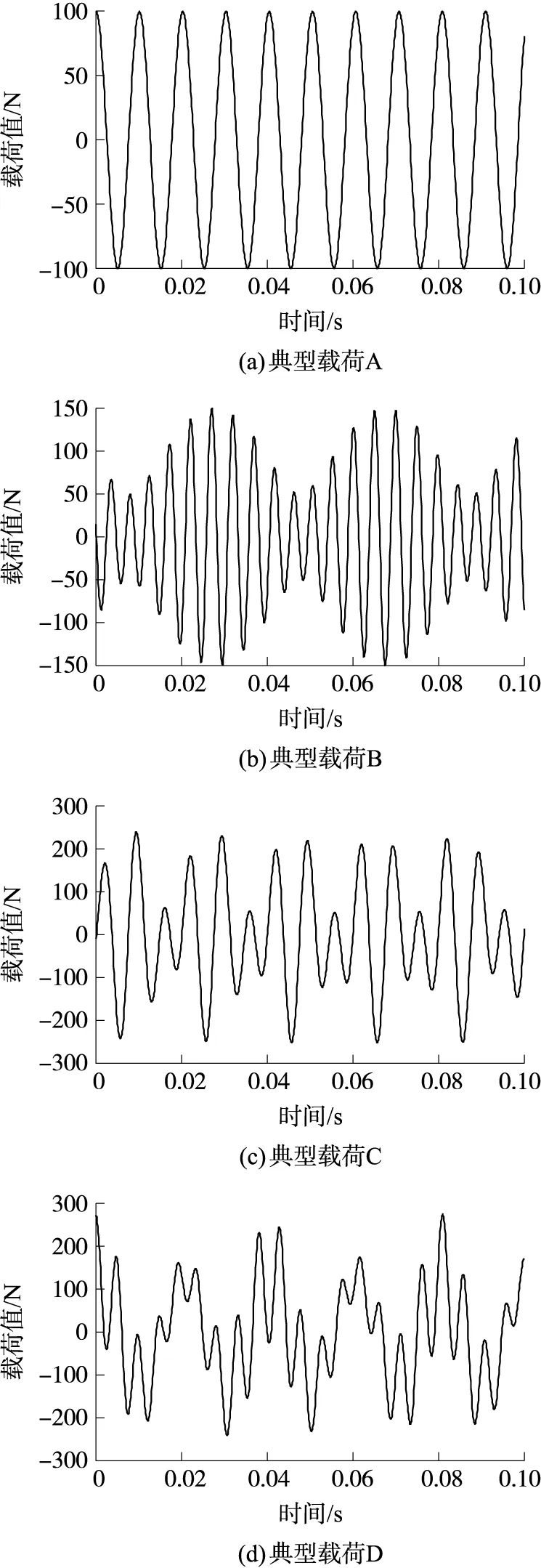
图8 典型信号的波形图Fig.8 Waveform diagram of typical signal

神经网络训练完成后,采用仿真模型获得测试数据对网络进行测试,测试结果如图9典型载荷识别结果所示。识别过程共历0.195 s,载荷识别相对误差0.97%,可见,本文方法对于典型载荷识别具有较高的精度,这也验证了本文所用的实验系统和神经网络用于载荷识别工作的可行性和正确性。

图9 典型载荷识别结果Fig.9 Typical load identification results

2 实验验证

图10 实验系统Fig.10 Experimental system

2.1 典型载荷识别验证

通过信号发生器产生典型载荷信号,通过功率放大器传输到振动激振器,使用激振器激励导弹模型,激振器通过力传感器与模型相连,用来采集实时载荷信号。模型上装有加速度传感器,用来采集加速度信号。本文共做了10组实验,使用这10组采集到的数据测试神经网络,其中网络的输入为加速度数据,输出为载荷数据,即力数据。为避免输入和输出数据因量级相差过大而对神经网络性能造成影响,测试前需要对数据进行归一化处理,之后在对预测结果数据进行反归一化。20组测试结果均表现良好。因篇幅有限,这里仅展示2种典型载荷识别结果。

由图11可知,相对误差分别为1.21%和1.37%。可见,经实验验证,上文所训练的神经网络对于实际实验也具有很强的适用性。对于火箭发动机地面振动实验具有重要意义。

图11 典型载荷实验验证结果Fig.11 Verification results of typical load experiments

2.2 随机载荷识别验证

导弹在飞行过程中受到的载荷往往具有强烈的随机性,因此有必要发展一种能够在地面映射空天随机载荷的方法。这对于发动机的设计研究以及燃烧不稳定的预测具有十分重要的作用。验证方法和模型的正确性后,开展了随机载荷识别的研究。

与上文一致,采用信号发生器产生随机载荷信号并传输到模态激振器,来激励导弹模型。同样,对测试数据进行归一化处理,对识别结果进行反归一化。随机载荷识别结果如图12所示。识别过程共历0.2 s。可见,神经网络识别结果良好,载荷识别相对误差可达1.82%。

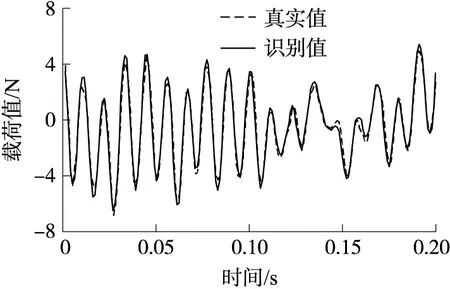
图12 随机载荷实验验证结果Fig.12 Verification results of random load experiment

3 结束语

本文加工了一种导弹的全弹模型,进行了有限元模态分析和模态试验,获取了典型振动模态频率,主要包括一阶弯曲模态和二阶弯曲模态。通过有限元仿真获取训练数据,训练神经网络。搭建了地面试验台进行实验,获取实验数据,测试神经网络,实现了对导弹典型载荷和随机载荷的识别,其中对典型载荷的识别相对误差为1.21%,对随机载荷的识别相对误差为1.82%。

本文方法能够较为精确地识别导弹飞行过程中受到的飞行动载荷,对于导弹结构设计和不稳定燃烧的预测与抑制工作具有较大帮助。