基于火炮膛内气固两相流的热散失模型数值仿真
王 克,张领科,王戴思源
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
习惯上将首发射击时火炮身管温度与环境温度内外均匀一致的情况称为冷炮[1]。实际射击时,由于内弹道过程中火药燃气温度可达到3 000 K以上,高温燃气会和身管内壁发生换热,导致一部分的气体内能因加热身管而损失,这部分损失的能量称为热散失。热散失会使燃气对弹丸做功减少,影响弹丸初速和火炮命中率。热散失过程使得身管内壁温度升高,引起火炮烧蚀。因此,膛内燃气的热散失是内弹道计算时需要重点考虑的因素之一[2]。常规的内弹道仿真计算一般是对火药力或者燃气的绝热指数k进行修正[3],以此考虑热散失对内弹道性能的影响,但这种修正方式不够精确。
针对上述问题,一些学者基于不同的内弹道模型研究了身管传热和热散失[4-6]。XIN等[7]优化了火炮射击过程中的能量转换过程,提高了热力系统的效率。JARAMAZ等[8]研究了4种类型的点火器对膛内两相流燃烧的影响,并开发了TWOPIB程序。文献[9]通过实验、数值和分析方法研究了炮管的热-机械耦合。AVANISH等[10]采用集总参数法,开发了一个内弹道程序,利用有限元方法模拟火炮身管温度随时间的变化,计算所得的膛内最高温度与LAWTON等[11]的GUNTEMP8程序计算结果一致。WOODLEY等[12]在CTA1内弹道程序中实现了枪管加热和烧蚀模型,并利用155 mm电热化学火炮(electrothermal-chemical gun,ETC)和改进的半密闭爆发器进行了验证。预测温度和测量温度之间获得了良好的一致性。CHEN等[13]通过对火炮身管外壁温度实时监测所得数据,利用加权输入估计算法计算出身管热流量和内壁温度,得出弹道热输入量会导致内壁温度达到材料熔点,导致身管烧蚀的结论。HU等[14]修改了火炮膛内两相流体流动模型,该模型可以补偿热力系统的热散失,但没有给出准确的热散失量。
本文在常规火炮气固两相流模型的基础上,将热散失模型与传热模型耦合,修正了两相流模型中的气体能量方程。根据155mm火炮的实验数据,探讨了热散失对火炮战术指标和身管传热的影响。
1 物理模型
图1为身管模型示意图,身管轴向分成1 660个网格,网格尺寸为5 mm,径向分为200个网格,网格尺寸为0.2 mm。装药结构采用布袋装药,底部有一个点火药包,内有130 g点火药(2#黑火药),剩余空间装一定量的发射药。表1和表2分别列出了火药参数和两种工况下实验测试结果。

图1 火炮身管模型示意图Fig.1 Schematic diagram of gun barrel model

表1 火药参数Table 1 Gunpowder parameters

表2 测试工况Table 2 Test conditions
2 数学模型
2.1 热交换模型
炮膛中的高温气体以对流和辐射的形式将热量传递到内壁。总热流可表示为
(1)
式中:Tg为气体温度;T0为身管内壁温度;h1为燃气与内壁之间的对流换热系数;εp为火药表面的黑度;玻尔兹曼常数σ0=5.670 32×10-8W/(m2·K4)。
考虑到火炮膛内属于大温差的旺盛湍流对流换热,故对流换热系数为[15]
(2)
Nu=0.023Re0.8Pr0.3
(3)
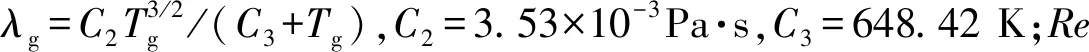
2.2 身管传热模型
2.2.1 传热方程
火炮发射时身管内轴向温度梯度远小于径向温度梯度,故仅考虑身管一维径向传热效应[9];考虑到身管的轴对称性,取其截面为研究对象,其径向传热示意图如图2所示。图中,Ta为环境温度,TN为身管外壁温度,T0为身管内壁温度,Tg为火药燃气温度,h2为环境空气和身管外壁之间的传热系数,h1为火药燃气和身管内壁之间的传热系数,R0和R1分别为身管的内、外半径。
身管径向无内热源一维传热微分方程为[16]
(4)
式中:导温系数a=λ/(ρc),λ为身管壁导热系数,ρ为身管材料密度,c为身管材料比热容;身管温度T是时间与半径的函数,即T=F(t,r);t为内弹道周期的总时间;r为身管内壁中任意点到中心的距离。
2.2.2 定解条件
①初始条件。
单发:T=Ta;
连发:T=F(t,r),F(t,r)是前一次射击引起的身管温度分布。
②边界条件[17]。
内边界条件:
(5)
外边界条件:
(6)
2.2.3 方程离散
为了求解需要对式(4)~式(6)进行离散化处理,时间项采用向前差分,空间上采用中心差分[18]。
身管内节点差分后方程为
(7)
该方程的稳定性条件为1-2Fo>0。
内边界差分方程为
(8)
外边界差分方程为
(9)
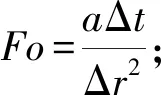
2.3 热散失模型
身管轴向x位置处Δx内微元面积上单位时间热散失量可以表示为
QL=qwΔS
(10)
式中:ΔS=πDΔx为热交换微元面积。
热散失量在气相能量方程中应表示为单位时间单位体积AΔx内散失的能量,故将上式改写为
(11)
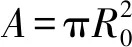
总热散失量对式(10)进行积分可得:
(12)
式中:l为身管总长度。
热散失量占火药燃烧产生的总能量的百分比为
(13)
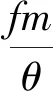
2.4 气固两相流模型
基本假设[17]:①忽略药包布袋的能量;②火药燃烧服从几何燃烧定律和指数燃烧定律,且火药颗粒不可压缩;③火药颗粒着火服从着火准则,即当火药表面达到着火温度时即认为火药着火;④火药颗粒在膛内均匀分布,并按连续介质处理,建立相应的质量、动量守恒方程;⑤不考虑底火药包的运动,假设底火的能量只在靠近膛底处空间直接释放;⑥燃气服从Nobel-Abel状态方程。
一维两相流模型写成如下守恒形式[19]:
(14)
式中:U,F,S分别为守恒矢量、对流项和源项。
(15)
(16)
(17)
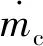
2.5 数值解法
对式(14)采用具有二阶精度的MacCormack差分格式[24]进行求解。
预估步:
(18)
校正步:
(19)
该格式的稳定性条件为[23]:
(20)
式中:c0为一个小于1的系数,取0.8~0.9;c为声速;对于每一个空间网格点都需要进行稳定性条件计算,取所有网格点中满足稳定性条件的最小时间作为时间步长。
2.6 边界条件
把膛底当作静止的固壁,如图3使用反射法,有:

图3 固壁边界条件反射法Fig.3 Reflection method of fixed wall boundary condition
u0=-u1,u=(ug,up)
q0=q1,q=(ρg,p,φ,T)
对于运动的弹底边界,应用运动控制体方法[20],得到:
对于气相速度,认为弹底气相速度等于弹丸运动速度,并满足弹丸运动方程:
式中:pd为弹底压力,pf为阻力,S为弹底面积,md为弹丸质量。
3 内弹道仿真结果与讨论
3.1 网格检验
对轴向和径向网格进行独立性验证,结果如图4所示。当轴向网格长度Δx=5 mm,径向网格长度Δr=0.2 mm时,可以在保证计算精度的同时提高求解速度。

图4 网格独立性验证Fig.4 Grid independence verification
3.2 两相流计算结果
图5显示了膛底和弹底处压力的时间历程。弹丸的位移和速度如图6所示。在两种工况下,初始阶段膛底压力均高于弹底压力,但随着燃烧的进行,短时间内会出现弹底压力高于膛底压力的情况。这是因为局部点火的方式容易引起反向压力波。随着弹丸运动,膛内压力逐渐趋于均匀,如图7所示。

图5 膛底与弹底压力Fig.5 Pressure at the bottom of chamber and projectile
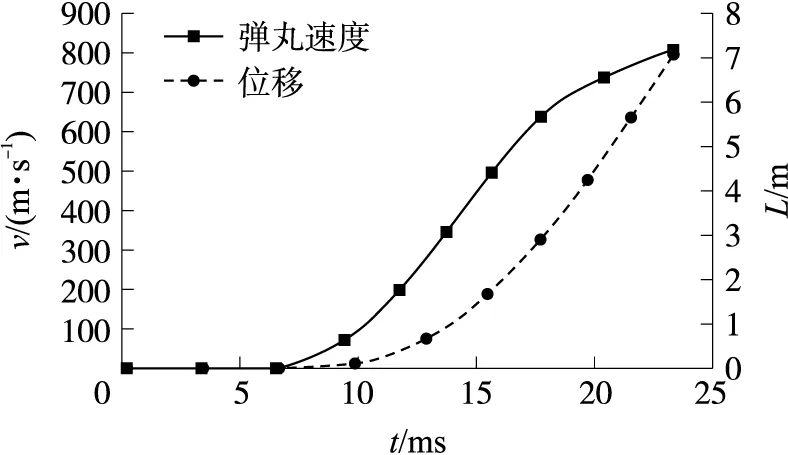
图6 弹丸速度与位移的时间分布Fig.6 Time distribution of projectile velocity and displacement
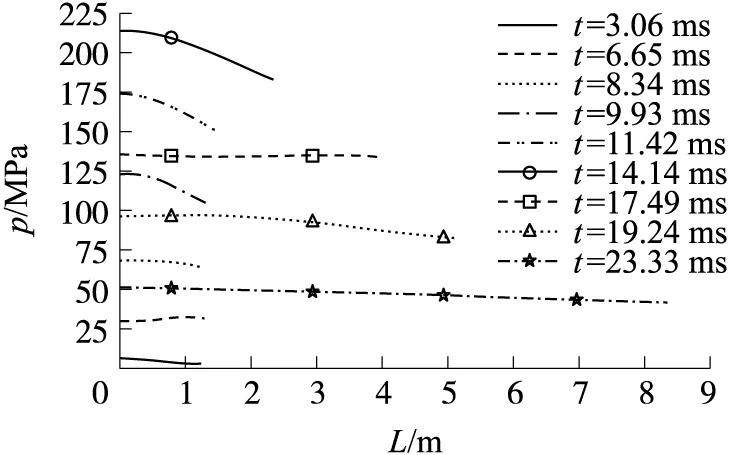
图7 压力分布Fig.7 Pressure distribution
初期靠近膛底位置的火药在底火能量下率先开始燃烧,所以膛底处孔隙率逐渐变大。燃烧产生的气体会推动火药颗粒向弹底方向移动,大量的火药颗粒在弹底部位聚集,火药被全部点燃会导致该处的燃气生成速率急速增加。膛内压力达到启动压力后开始推动弹丸运动,此后弹后空间变大,孔隙率急速升高。随着火药的燃烧以及弹丸的运动,膛内空间孔隙率逐渐趋近于1,如图8所示。

图8 孔隙率Fig.8 Porosity
不同时刻膛内气相和固相速度沿轴线分布曲线如图9、图10所示。弹丸未运动时,膛内气相和固相速度不断升高,速度峰值从膛底逐渐向弹底方向移动,当出现反向的压力梯度时火药燃气和颗粒会在压力作用下向膛底方向运动。一旦弹丸开始运动,弹底边界处气相和固相速度不再为0,并随弹丸运动速度的增加而不断增大,且弹后空间气固两相的速度沿轴向基本呈线性分布,满足拉格朗日假说的内容。由于固体颗粒具有惯性,因此固相速度始终小于气相速度,这种现象在整个内弹道时期都是存在的。
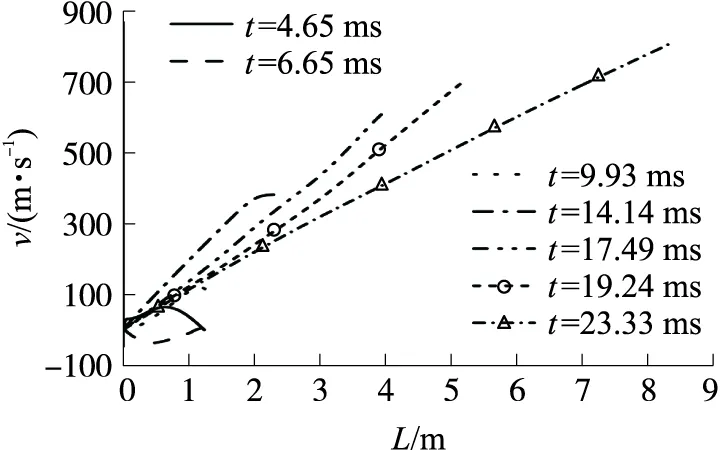
图9 气相速度分布Fig.9 Gas velocity distribution
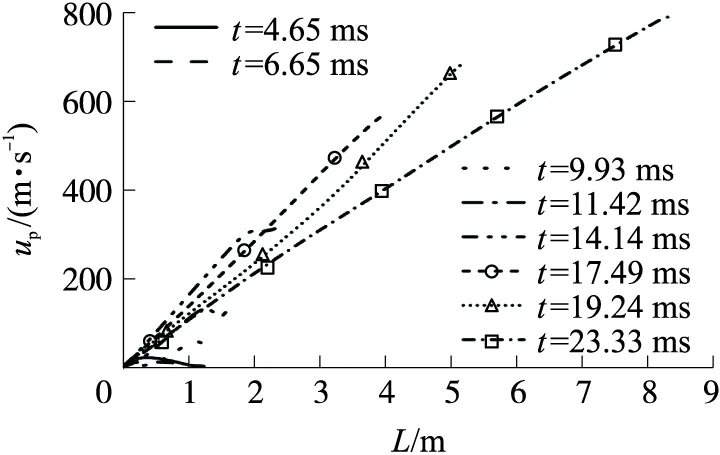
图10 固相速度分布Fig.10 Solid velocity distribution
3.3 热散失对内弹道过程的影响
目前通常采用从膛线起始2.54 cm处(本文中约为距膛底L=1.07 m处)的内径增量,作为火炮身管烧蚀的衡量标准[25-26]。因此本文重点考虑热散失对该位置处的燃气及身管径向温度分布的影响。
两种工况下目标位置处的对流换热系数如图11所示,对流换热系数的变化趋势和到达峰值的时间与膛内压力曲线相似,这是因为对流换热系数受气体速度和火药气体密度影响很大,随着火药燃烧火药气体密度增大,火药气体压力随之升高,弹丸加速运动,火药气体速度增加,对流换热系数增大;反之,随着弹丸持续加速运动,弹后空间不断增大,火药气体密度由增长转为下降,火药气体压力随之下降,火药气体密度与火药气体速度乘积变小,相应火药气体雷诺数变小,进而导致对流换热系数下降。虽然对流换热系数和膛内温度随弹后空间的增大而降低,但与燃气发生对流换热的内壁面积在不断增大,因此两种工况下的总热散失量随时间不断增加,如图12所示。
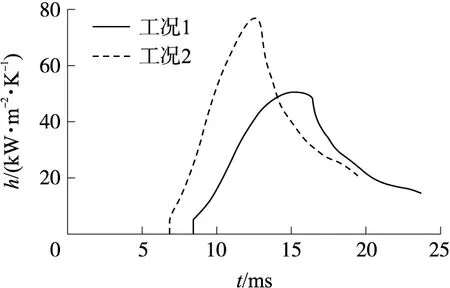
图11 对流换热系数(L=1.07 m)Fig.11 Convective heat transfer coefficient (L=1.07 m)
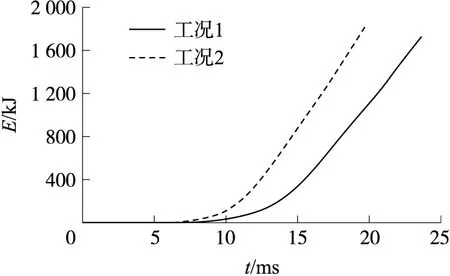
图12 总热散失量Fig.12 Total heat loss
考虑对流和辐射以及仅考虑对流的热散失情况如表3所示,两种工况下的热散失误差分别为3.39%和2.63%。因此,膛内的传热过程主要依赖对流传热,热辐射可以忽略不计。

表3 对流和辐射散热量Table 3 Convection and radiation heat dissipation
距膛线起始2.54 cm处(L=1.07 m)的身管径向温度分布如图13所示,内壁在高温燃气的对流换热作用下温度最高可达1 047.5 K左右,到达内壁的热量通过导热的形式在身管内部传递,沿身管径向方向温度逐层降低,距内壁r=1.0 mm处的温度最高只有430 K。内壁及靠近内壁位置的温度随时间出现先增加后降低的趋势。一方面是因为燃气温度的下降,对流换热的驱动力温差减小;另一方面该位置处的燃气密度与燃气速度乘积的减小导致燃气雷诺数下降,进而造成对流换热系数下降。
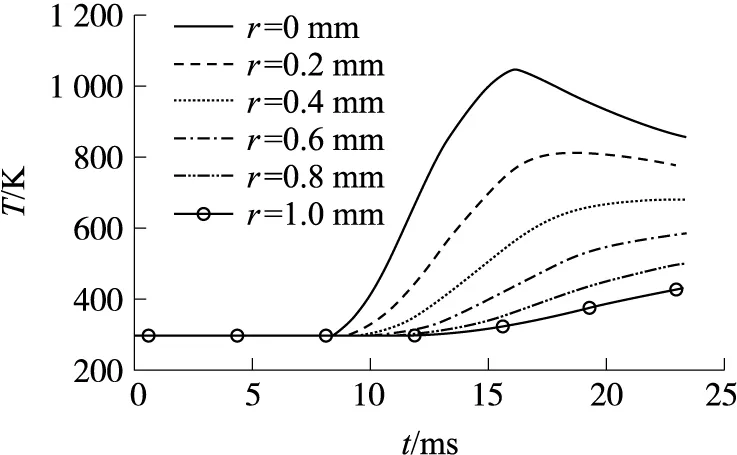
图13 身管径向温度分布(L=1.07 m,工况1)Fig.13 Radial temperature distribution of barrel (L=1.07 m,condition 1)
表4列出了两种工况下的膛压和初速结果。与实验结果(见表2)相比,在工况1下,采用热散失模型时,最大膛压误差为0.99%,初速误差为0.20%,L=1.07 m处的最大内壁温度为1047.5 K。单次发射时的热散失占发射药燃烧产生的总能量的3.43%(如式(13))。在工况2下,采用热散失模型时,最大膛压误差为0.57%,初速误差为0.25%,L=1.07 m处的最大内壁温度为1 200.5 K。热散失占发射药燃烧产生的总能量的2.98%。考虑热散失模型时计算的膛压和初速与实验结果吻合较好。
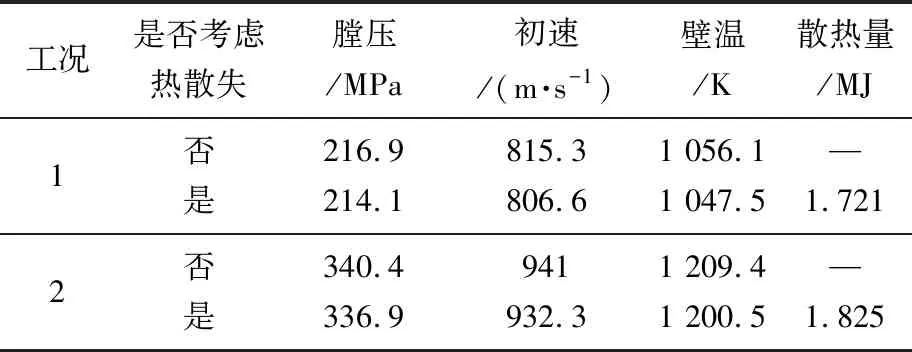
表4 计算结果Table 4 Calculation results
4 结束语
本文对常规的气固两相流方程进行修正,主要在气相能量方程中考虑了热散失量的影响,采用C语言编写程序大大提高了计算速度,准确地描述出火炮发射过程中膛内气固两相流场参量的变化情况。基于两相流的计算结果,结合身管传热模型,得到身管内壁径向温度分布情况,并讨论了热散失对内弹道性能的影响。计算结果与实验数据进行对比分析,结果表明:①考虑热散失的两相流模型计算的最大压力误差小于1%,初速误差小于0.5%。②热散失占火药燃烧产生的总能量的2%~4%。③在身管径向温度分布中,内壁最高温度可达1 200 K以上,温度沿径向逐层下降,距内壁1 mm范围内温度梯度较大。
上述结论证明了本文提出的热散失模型的可行性和优越性,为弹道仿真提供了更准确的预测和计算手段。

