枪面侧倾对外弹道的影响及修正方法

艾 川,朱开钰,李东昊,李小平

(重庆建设工业(集团)有限责任公司,重庆 400054)

在射手有侧倾射击习惯或受地形限制,狙击步枪架设不平时,造成枪面(包含瞄准线与枪膛轴线的平面)与地面不垂直,产生横向倾斜,称为枪面侧倾,枪面与铅垂面之间的夹角称为侧倾角。枪面侧倾时,尤其是在侧倾角较大时,弹道将偏向一侧,而且会给弹着点的高低带来较大偏差[1]。文献[1]给出了计算弹道偏差的几何关系,但未对该几何关系作出分析和推导,也未给出计算弹道下降量的方法,难以指导实践应用。通常,狙击枪在射击时横向倾斜造成的偏差可通过狙击枪下搭配的支架来消除[2]。但是,苏宁等[3]在介绍国外狙击手比赛科目时指出,由于执行任务时的射击环境限制无法正常射击,需要倾斜枪面进行射击,枪面倾斜射击已成为各类狙击比赛常设科目。鄢砚军等[4]对狙击步枪弹丸有效射程轨迹内的受力情况进行了分析,研究了空气阻力、重力、风和弹丸速度等因素对弹丸运动轨迹的影响,基于Matlab对弹丸的弹道解算算法和自动校正算法进行了实现,但未进行枪面侧倾时的弹道校正分析和实现。郑玉辉等[5]研究了某反坦克导弹侧倾射击时的弹道偏差,通过受力分析和坐标系变换,建立了弹道偏差数学模型,依据地面坐标系与瞄准镜坐标系之间的关系,提出了侧倾射击时弹道偏差修正与操作方法。张胜三[6]采用几何分析法验证了坐标系变换法的正确性,针对多管火箭发射车采用调平保证瞄准精度而存在的问题,提出根据发射车纵轴、横轴的倾角值,推导出瞄准角修正量的计算公式,实现不进行发射车调平而采用瞄准角修正的方法,来保证瞄准精度。贾波等[7]在基于弹箭飞行诸元精确测量结果的基础上,通过理论研究和仿真计算,对弹箭气动参数准确辨识方法和弹道全面符合计算方法进行了研究,形成了射表编拟新方法,但未对偏流测试方法进行研究。

本文采用几何方法分析了枪面侧倾对外弹道的影响和弹着点偏差分布规律,推导出了枪面侧倾射击时的弹着点偏差计算公式,研究了弹道修正方法,提出了计算弹道修正量的方程组,以期为某型7.62 mm高精度狙击步枪在实战应用中进行枪面侧倾射击提供弹道装定参考,同时为测量弹丸偏流提供了新的试验方法参考。

1 枪面侧倾对外弹道的影响

1.1 弹着点偏差分析

在100 m射距处,利用三维设计软件,采用几何方法分析枪面侧倾后的弹着点变化。忽略枪械射击时的跳角和弹丸旋转产生的偏流,建立枪面与地面垂直射击时的地面坐标系,用Oxyz表示,以弹道起点为坐标原点,以射击面和弹道起点水平面的交线为z轴,沿射向为正,y轴铅直面向上为正,x轴方向按右手法则确定[8]。如图1所示。

某型7.62 mm高精度狙击步枪使用光学瞄准镜作为瞄具。图1中H点为瞄准镜分划中心点;lHM为瞄准镜光轴与枪膛轴线高度,定义为瞄准镜高度,其值为64 mm;γ为瞄准镜高角。设瞄准点L在枪口水平线上,即高低角为0°,OL为枪口水平线,lOL为射距。OM为枪膛轴线;lOM为枪口与瞄准镜分划中心点在枪膛轴线上的投影距离,其值为668 mm;HL为瞄准线;OT为仰线,也是射线。从图1中可得出,枪膛轴线OM与射线OT共线,A点为射线OT与瞄准线HL的交点。曲线OAL为弹道曲线,∠LOT为射角β,向上为正,∠LAT为瞄准角α。在瞄准点L处建立一个垂直于坐标轴z的弹着点平面CDEF,如图2所示。

图2中点T为枪膛轴线OT在弹着点平面上的指向点,在狙击步枪完成归零后,瞄准点L即为弹着点,lTL为弹道下降量,其值为负。进行枪面侧倾射击时,瞄准线HL仍然指向瞄准点L,枪膛轴线OM则以A点为支点绕瞄准线HL沿射向逆时针转动一个侧倾角δ。侧倾角δ为平面HMLT与平面HM′LT′的夹角,并非∠MHM′。如图3所示。

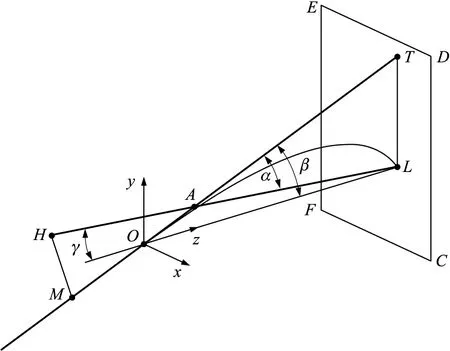
图2 弹着点平面示意图Fig.2 Plane diagram of the point of impact

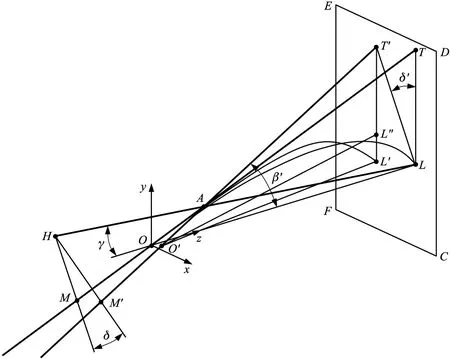
图3 枪面侧倾示意图Fig.3 Sideways tilting diagram of gun surface

从图3中可以看出,枪面侧倾后,枪膛轴线OM绕点A旋转到O′M′ 并指向弹着点平面平面CDEF上的点T′,即射线变为O′T′,在高低和方向均产生了相应的偏差。在CDEF上通过T′点作平行于TL线的直线T′L′,设点L′为枪面侧倾后的弹着点,曲线O′AL′为侧倾后的弹道曲线。侧倾后的射距为枪口O′到直线T′L′的垂直距离,设为lO′L″。射角变为侧倾后的射线O′T′与Oxz的夹角β′。δ′为T′L与TL的夹角。计算点L′位置,即可得出枪面侧倾射击的弹着点偏差。

根据某型7.62 mm高精度狙击步枪的射表编拟数据,在100 m射距处的射角为0.049°。利用三维设计软件,采用几何法计算枪面侧倾不同侧倾角后的射角β与射距lOL,结果如表1所示。

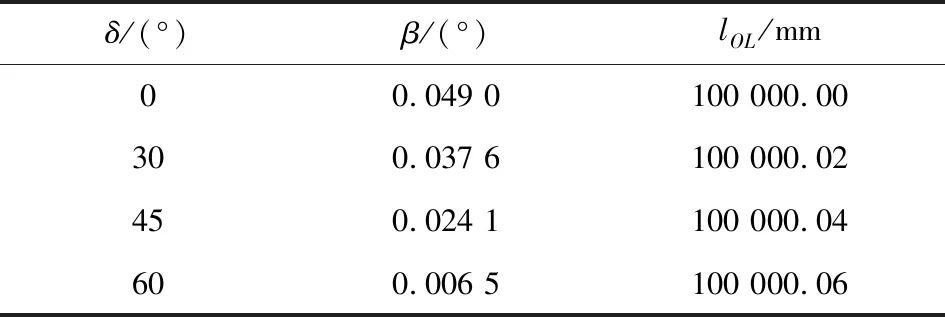
表1 枪面侧倾后的射角和射距Table 1 Angle of departure and range after the gun face is tilted sideways

从表1中可看出,枪面侧倾后,虽然射角β发生了明显的变化,但是变化量小于0.05°,根据弹道学刚性原理[9],枪面侧倾后弹道下降量基本不变,即lT′L′=lTL。枪面侧倾后射距变化差异非常小,可以忽略。射距lOL值远大于瞄准镜高度lHM值,经计算,在100 m射距处形成的瞄准镜高角γ仅为0.036°,几乎垂直于弹着点平面CDEF,同时由于射角β也很小。枪面绕瞄准线HL旋转时,相当于绕z轴旋转,即射线OT绕枪口水平线OL画圆。如图4所示。

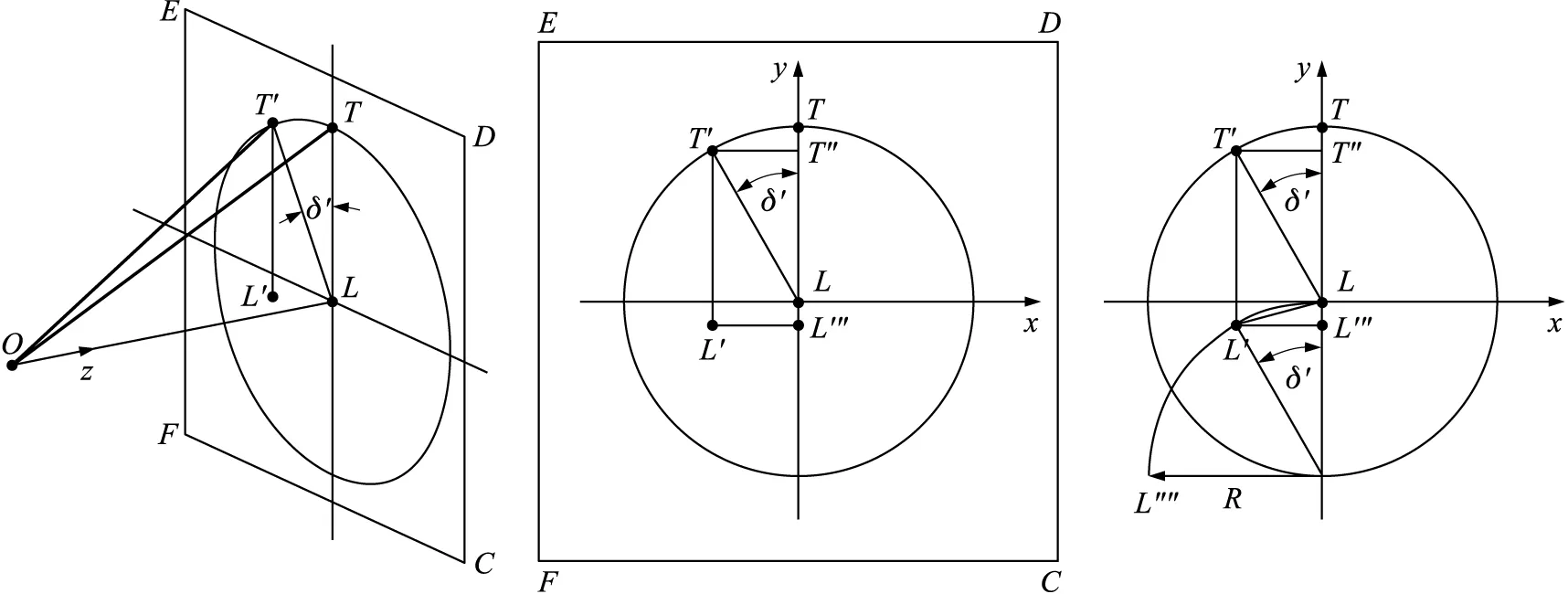
图4 弹着点偏差示意图Fig.4 The schematic diagram of the point-of-impact deviation

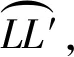
(1)

式中：Δx为方向偏差,向右偏为正;Δy为高低偏差,向上偏为正;lL′L为弹着点与瞄准点的偏差距离,Δε为偏差距离在射距处对应的偏差角。

利用三维设计软件,采用几何法计算枪面侧倾后的δ′值,结果如表2所示。

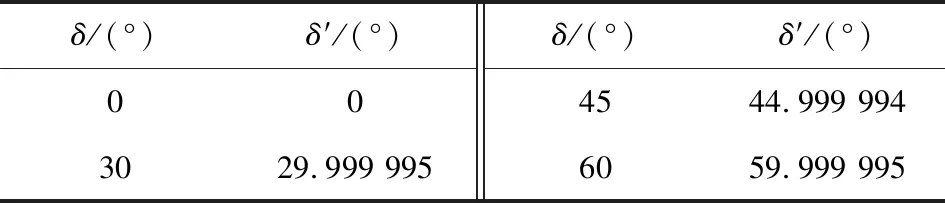
表2 枪面侧倾后的δ′值Table 2 δ′ value after the gun face is tilted sideways

从表2中可看出δ′≈δ,取：

δ=δ′

(2)

从图1所示几何关系可得弹道下降量：

lTL=-tanβlOL

(3)

将式(2)和式(3)分别代入式(1)即得出枪面侧倾后弹着点偏差：

(4)

当无射表数据,或受弹道条件、气象条件等影响时,需要根据实时条件进行计算或实验测试弹道下降量。测试弹道下降量的方法：首先在5 m的近距离射距,将平均弹着点矫正到瞄准点正下方,距离为瞄准镜高度lHM,再瞄准远距离处的瞄准点射击,测量瞄准点与平均弹着点之间的垂直距离,该距离减去瞄准镜高度lHM即为弹道下降量lTL。

根据式(4),在100 m射距处,引用射表数据,进行不同侧倾角弹着点偏差计算,结果见表3。

表3 不同侧倾角弹着点偏差Table 3 Point-of-impact deviation in different sideways-tilting angles

根据式(4),以枪面侧倾2°为例,引用射表数据,进行不同射距处的弹着点偏差计算,结果见表4。

表4 不同射距处弹着点偏差Table 4 Point-of-impact deviation at different ranges

从表4中可以看出,枪面侧倾时,弹着点高低和方向偏差均随射距增加而变大。当侧倾角很小,仅2°时,高低偏差变化很小,方向偏差增加显著。偏差角随射距的增加而显著加大。在100 m射距处,偏差角仅为0.1′,可以忽略;但在300 m射距处,偏差角增大到0.35′,超过高精度狙击步枪的密集度指标的1/3,不容忽视。由于偏差角随射距的增加而加大,对应的弹道修正角度也随之加大,因此,近距离射效矫正不能消除枪面侧倾对远距离弹道偏差的影响,在近距离进行射效矫正时,也应保持枪面垂直,以减小因枪面侧倾导致的远距离弹道偏差;同理,近距离的射击密集度不能反应出射手据枪稳定性,不能用近距离射击密集度评价和考核射手据枪稳定性。由于射手操作差异,使用其他射手在近距离矫正的枪支进行远距离射击时,会存在较大的弹道偏差。因此,每一名射手,不论是近距离射击还是远距离射击,保持枪面垂直同等重要,应加强远距离射击训练,以考核射手据枪稳定性。

1.2 修正方法

某型7.62 mm高精度狙击步枪采用白光瞄准镜作为瞄准具,设置有方向和高低修正手轮。枪面侧倾后,修正瞄准镜手轮使弹着点移动的方向如图5所示。

图5 侧倾修正示意图Fig.5 Sideways-tilting correction diagram

图5中xLy为弹着点平面,x和y分别为弹着点的方向和高低坐标。x′和y′分别为修正瞄准镜方向和高低手轮时,弹着点移动方向。从图中几何关系可得,调节手轮使弹着点产生的移动量为

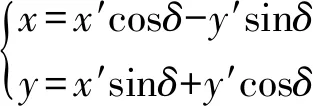
(5)

式中：x为方向(水平)移动量,其目标值为-Δx;y为高低(竖直)移动量,其目标值为-Δy。式(5)即为枪面侧倾射击时的弹道修正方程组。

将式(4)代入式(5),求解即可得出瞄准镜在方向和高低手轮上的弹道修正量x′和y′：

(6)

从式(6)可以看出,瞄准镜方向手轮修正量为弹着点方向偏差的负值,瞄准镜高低手轮修正量即为弹着点高低偏差值。可用此方法快速装定瞄准镜。

2 实验验证

2.1 实验方法

为避免射手、气象、地理等外部条件对射击精度造成的影响,实验设置在室内靶道进行。射距100 m,室温14.1 ℃,湿度68.7%,气压996.5 hPa。将狙击步枪的枪管通过专用接口固定连接在高低和方向均可调的STZA12MA型射击精度实验台上,使用光电靶记录弹着点坐标。实验装置如图6所示。

图6 实验装置Fig.6 Experimental facility

弹着点偏差实验方法和步骤如下：

① 在枪面垂直时进行射效矫正,即将瞄准镜分划中心调整到0°射击时的平均弹着点,将该点设置为瞄准点和坐标原点。

② 重新固定枪支,将枪面侧倾到预定角度;调节实验台,使瞄准镜分划中心对齐瞄准点,进行射击试验。

③ 每个角度连续射击7发[1],以减小平均弹着点的公算偏差,记录平均弹着点坐标值。每组射击完成后均清洁枪膛,并将枪膛冷却至接近室温。

采用分划调节精度为0.25′的瞄准镜,进行弹道修正的实验方法和步骤如下：

① 根据枪面侧倾弹道偏差实验值,采用快速装定法计算出高低和方向修正量,并取整为瞄准镜手轮调节格数,然后计算实际修正量及修正误差。

② 将弹道偏差实验值代入式(5)精确计算出高低和方向修正量,并取整为瞄准镜手轮调节格数。然后计算实际修正量及修正误差。

③ 对两种方法的修正误差进行对比。

2.2 实验结果及讨论

枪面侧倾弹着点偏差实验结果见图7所示。图中,弹着点旁方框内数据为侧倾角度和坐标值。从图7可以看出,弹着点偏差随侧倾角的变化轨迹基本符合圆弧形分布。但枪面右倾时弹着点比左倾时偏高,在90°时最为明显;同时,将枪面侧翻射击时(即侧倾180°),弹着点偏右。造成这种现象的原因是：某型7.62 mm高精度狙击步枪枪管膛线设计为右旋,弹丸旋转导致弹丸向右下方偏,产生了偏流;枪面垂直射效矫正时,由于偏流导致瞄准线HL与射击面yz存在偏流夹角。这为测试弹丸偏流值提供了一种新的试验方法,即先将枪面在铅垂方向进行射效矫正,再分别向左和向右侧倾90°射击,其弹着点坐标高低差的一半即为该射距处的偏流。

图7 弹着点偏差实验结果Fig.7 Experimental results of the point-of-impact deviation

与表3相比,弹着点偏差值差异比较大,其原因是采用固定架射击与人工射击产生的跳角,以及试验时的弹道、气象条件差异造成的。因此,在进行枪面侧倾射击时,应以实时射击产生的弹着点偏差值计算修正量。

枪面侧倾后,使用快速装定法计算的弹道修正结果见表5。使用式(5)精确计算的弹道修正结果见表6。

表5 快速修正结果Table 5 Rapid correction results

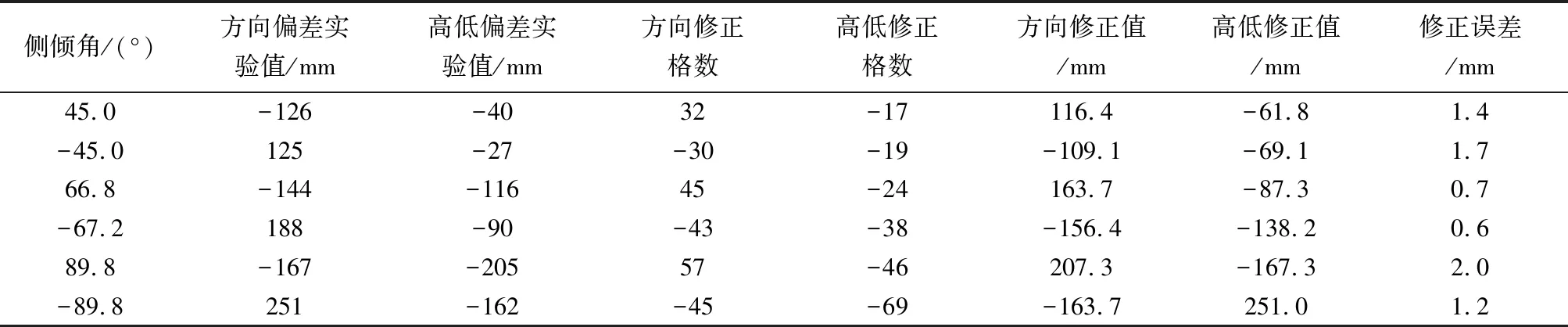
表6 精确修正结果Table 6 Precise correction results

从表5中可看出,由于偏流导致弹着点偏差分布规律与圆弧有差异,采用快速装定法修正时,存在一定的误差,且向左侧倾时的修正误差小于向右侧倾时。从表6中可看出,根据式(5)进行精确修正的准确度较高,修正误差与瞄准镜的分划调整精度相关。

3 结论

①在100 m射距,侧倾角≤10°时,枪面侧倾引起的方向偏差显著大于高低方向;侧倾角达到10°时会显著影响射击准确度。

②枪面侧倾引起的弹道偏差角随射距的增加而加大,对应的弹道修正角度也随之加大,在近距离进行射效矫正不能消除枪面侧倾对远距离弹道偏差的影响。

③近距离的射击密集度不能反应出射手据枪稳定性,不能用近距离射击密集度评价和考核射手据枪稳定性;每一名射手,不论是近距离射击还是远距离射击,据枪时保持枪面垂直同等重要,应加强远距离射击训练,以考核射手据枪稳定性。

④由于跳角、弹道条件和气象条件的差异,枪面侧倾射击时的弹道偏差与采用射表数据进行计算的结果会存在明显差异。应根据实测弹道偏差,进行弹道修正。

⑤由于偏流的影响,枪面侧倾射击时,弹着点随侧倾角的变化轨迹并不完全呈圆弧形。枪面向左侧倾时,使用快速装定法进行弹道修正误差较小。枪面侧倾90°和-90°,只需交换高低和方向手轮进行弹道修正即可。根据枪面侧倾弹道修正方程组进行精确修正的准确度较高,修正误差仅与瞄准镜的分划调整精度相关。

⑥先将枪面在铅垂方向进行射效矫正,再分别向左和向右侧倾90°射击,其弹着点坐标高低差的一半即为该射距处的偏流。

本文给出的弹着点偏差计算公式不适用于射角较大的曲射武器,也不适用于交汇点A在射距之外的武器。