高强度聚焦超声治疗浅表组织的仿真研究
刘 力,刘 闯,朱巧苗,李雁浩,2*
(1.重庆医科大学 生物医学工程学院 超声医学工程国家重点实验室,重庆 400016;2.超声医疗国家工程研究中心,重庆 401121)
高强度聚焦超声(High-Intensity Focused Ultrasound,HIFU)是近年来发展迅速的一种无创局部高温治疗技术,该技术将体外发射的多组超声波聚焦于肿瘤细胞组织[1],聚焦超声在生物组织中形成的凝固性坏死区域被定义为生物学焦域[2],声能量的吸收不仅代表了能量的耗散,还会导致靶组织温度升高和热量的沉积,基于聚焦超声在生物学焦域处能量叠加产生的生物学效应(由HIFU 诱导的组织消融的主要机制包括热效应、空化效应和机械效应[3-4]),使得肿瘤组织温度瞬间上升到65 ℃以上,从而导致蛋白质变性产生不可逆的细胞损伤,达到消融肿瘤细胞的目的。
目前,HIFU 技术在浅表组织的临床治疗领域已得到越来越广泛的应用,其在治疗外阴白色病变[5]、宫颈炎[6]和皮肤美容[7]等领域已经积累了丰富的临床治疗经验。在浅表组织的临床治疗过程中,存在由于皮肤组织的物理特性会使皮肤表面沉积过多能量导致发生皮肤灼伤的情况,因此临床医师在术前选择合适的治疗参数和制定治疗方案对确保治疗过程的安全性和有效性十分重要。温度作为在临床治疗过程中最直观的可观测物理参数使得在治疗过程中获取组织的温度场特性极为重要[8],对临床医师选择合适的治疗参数具有重要意义,因此在制定术前治疗计划前对靶组织热场分布和损伤面积的预测是不可或缺的一步。
数值仿真工具的广泛应用使得在术前对治疗过程的模拟和参数预测更加简便,常诗卉等[9]构建了一种三维数值仿真模型探究在叠加双焦点的情况下调控信号激励时间差和幅值对HIFU 焦域温度场分布和焦域形状大小的影响。Meaney 等[10]构建了一种三维有限元模型计算得到聚焦超声消融病变组织过程中的温度场分布,结合热计量算法预测病变组织形状。张千等[11]采用数值仿真方法计算经颅骨治疗的温度场分布,并研究了治疗参数(输入声强、辐照时间)及换能器与颅骨相对距离对颅内形成焦域体积的影响。
本文基于K-wave 仿真工具包构建了高频聚焦超声换能器三维仿真模型,模拟高频聚焦超声换能器辐照浅表组织的实际治疗过程,分别利用Westervelt 方程和Pennes 生物传热方程求解声场和温度场分布。介质物理属性在空间域中的分布并非为理想的均匀分布条件,因此比较了介质物理属性在均匀和非均匀分布条件下求解的声场和温度场差异性,分析介质分布条件对声场和温度场的影响,此外采用3 种辐照模式探究了激励时间和间歇时间对温度场变化的影响,且预测了在换能器不同辐照模式下靶组织的凝固性坏死面积,为临床医师在制定术前方案时提供了可参考的治疗参数。
1 数值仿真理论
1.1 Westervelt 方程
本研究采用Westervelt 方程计算基波和谐波声场的分布,该方程考虑了声波在传播过程中的衰减、非线性效应、波散射和反射的影响[12],能够较为精确地计算有限振幅声波的非线性传播[13]
式中:∇ 代表拉普拉斯算子;p 为声压;c 为声波传播介质的声速;声扩散率,α 代表声波传播介质的声吸收系数,角频率ω=2πf,f 代表聚焦超声换能器的激励信号频率;β 为声传播介质的非线性系数;ρ 为声传播介质密度。超声波聚焦在靶组织处时由于组织对声波的粘滞吸收,部分声能量会转换为热量成为聚焦超声的加热热源,靶组织在单位时间内单位体积吸收的聚焦超声加热热源可由声强梯度空间公式Q=-∇·I 计算得到[14],其中声强,本文取n=4计算到最高四次谐波的声场分布,此时Q 可表示为
1.2 Pennes 生物传热方程
物体一般的传热方程
其物理意义是热传递物体内热量积累的总效果等于该物体控制边界热流流入、流出的积分[15]。在该方程的基础上考虑生物组织的血流灌注作用,在式(3)中加入血液灌注项得到Pennes 生物传热方程[16]
式中:ρ0为组织密度;C 为组织比热;T 为组织温度;λ为组织导热系数;Wb为血液灌注率;Cb为血液比热;Ta和Tv分别为动脉血温度与静脉血温度;Q 为高频聚焦超声换能器产生的加热热源。
1.3 等效热计量
用等效热计量的方法可以预测靶组织凝固性坏死面积,计算公式如下[17]
式中:T 为辐照过程中t 时刻的组织温度;R 为常数,取值随着组织温度的变化而变化,R=0.5(T≥43),R=0.25(T<43)。本文将等效热计量大于240 min 的区域定义为治疗结束后靶组织的凝固性坏死区域。
2 仿真模型构建与仿真参数
2.1 仿真模型
基于K-wave 仿真工具构建中心开孔的聚焦超声换能器三维仿真模型,如图1 所示。仿真模型由换能器、脱气水和两层浅表组织组成,模拟聚焦超声换能器在脱气水环境下发射超声波经过皮肤到达脂肪组织的过程,其中换能器焦距F 为9.5 mm,换能器外孔径a 和中心开孔内径b 分别为12.2 mm 及5.6 mm,换能器阵元表面距离组织的距离c 为3 mm,皮肤厚度d 为2 mm,脂肪厚度e 为6.8 mm,组织宽度g 为14.1 mm。

图1 仿真模型示意图
2.2 仿真参数
仿真模型计算中使用的介质属性参数见表1,基波与谐波对应不同介质的声吸收常数见表2。

表1 介质属性参数

表2 介质声吸收常数Np·m-1
3 仿真结果
在仿真计算中,选择频率为11.2 MHz 的正弦波作为换能器的激励信号,以换能器阵元幅值为0.1 MPa的表面初始压力表征换能器辐照组织时的输出能量大小,设置换能器以不同辐照模式(T1:2s-1s-5c,T2:2s-2s-5c,T3:3s-1s-5c,激励时间-间歇时间-治疗回合)输出信号,分析在不同仿真条件下换能器辐照域内的声场和温度场分布特性,计算靶组织声轴面方向凝固性坏死面积。
3.1 声场计算结果
由于换能器激发的声波聚焦在组织处会使得焦域处声压的幅值变得较高,导致声波的传播过程不再是线性的,会在声传播过程中产生高次谐波,而高次谐波对计算温度场产生的影响是不可忽略的,因此在计算声场分布时需要考虑声波传播过程的非线性效应[18]。如图2 和图3 所示,计算了介质物理属性在均匀和非均匀分布条件下沿换能器辐照域声轴面方向基波及谐波声场的分布,图4 为2种介质分布条件下沿换能器声轴线方向的声压幅值分布。

图2 介质均匀分布条件下沿声轴面方向声场计算结果

图3 介质非均匀分布条件下沿声轴面方向声场计算结果

图4 2 种介质分布条件下沿换能器声轴线方向的声压幅值分布
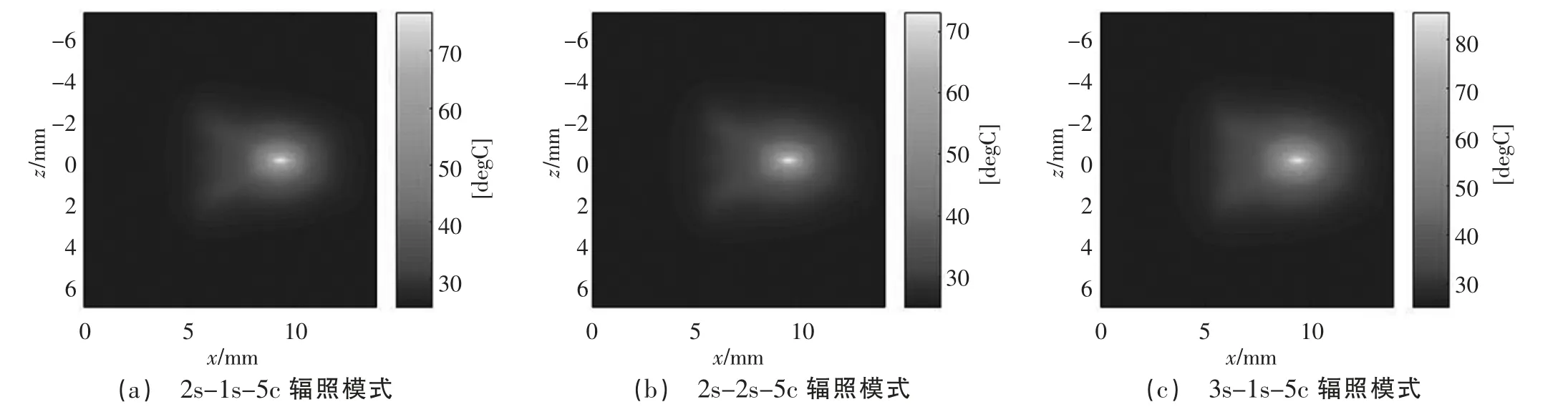
图5 介质均匀分布条件下不同辐照模式治疗结束时刻温度场分布
如图2 和图3 所示,换能器激励信号产生的声能量聚焦在焦域处产生的非线性效应会导致谐波的产生,从而会影响温度场的计算结果。基波同高次谐波相比,在焦点处的声压幅值最大,因此基波沉积的声能量作为高频聚焦超声的加热热源主要输入项,此外二次谐波和三次谐波对温度场的温度计算也需考虑,四次谐波声压幅值已相对较小,因此在计算声场时考虑到计算域的空间采样率和时间步长大小选择最高计算到四次谐波。
图4 分析了在不同介质分布条件下沿换能器声轴线方向的声压幅值分布情况,在声轴线方向上介质非均匀分布条件下的声压幅值普遍高于均匀分布,且在换能器几何焦点处最为明显。声能量主要分布集中在换能器辐照域的几何焦点处,此外在换能器阵元及皮肤组织界面处有一部分声能量被反射和吸收导致声压幅值较高,因此在构建仿真模型时应考虑实际治疗环境中组织的几何特性和物理特性,提高仿真模型的精确性,避免在临床治疗过程中由于皮肤组织的粘滞吸收导致声能量转换为热能引起皮肤灼伤。
3.2 温度场计算结果
以Westervelt 方程计算得到的换能器几何焦点处的时变声压作为输入项带入式(2)可得到加热热源Q,利用Pennes 生物传热方程计算温度场的分布。图5 至图8 为2 种介质分布条件在换能器不同辐照模式下的温度场计算结果。图9 和图10 为在温度场的计算结果基础上得到的辐照域内靶组织凝固性坏死面积。

图6 介质非均匀分布条件下不同辐照模式治疗结束时刻温度场分布

图7 介质均匀分布条件下不同辐照模式焦点处的温度变化曲线
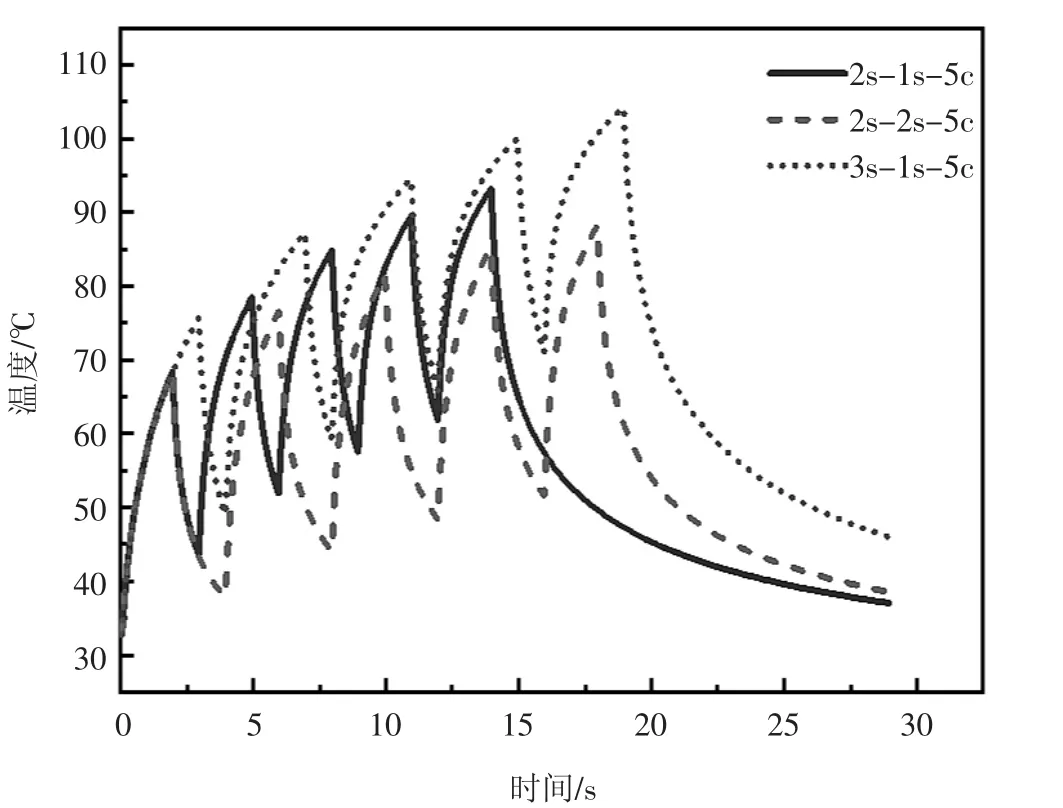
图8 介质非均匀分布条件下不同辐照模式焦点处的温度变化曲线

图9 介质均匀分布条件下不同辐照模式形成的凝固性坏死区域
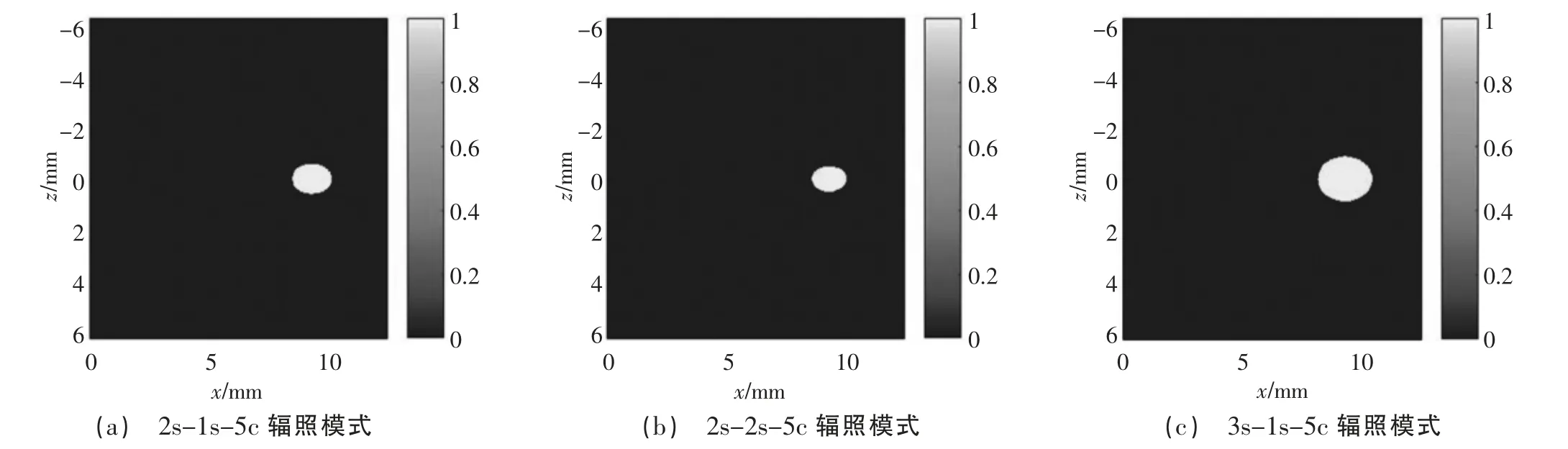
图10 介质非均匀分布条件下不同辐照模式形成的凝固性坏死区域
如图5 及图6 所示,热沉积能量主要集中于换能器焦点附近,温升最明显区域与图2、图3 中声压幅值大小的分布情况相对应。由图7 和图8 可知,随着激励时间的增加,温度上升幅度相对较高,可见激励时间和间歇时间的变化对温度场有较大影响。因此在临床治疗过程中可根据所需消融的病变组织大小选择合适的治疗参数,对所需治疗体积较大的病变组织可采用稍长的激励时间消融大部分所需治疗区域,再结合较长的间歇时间治疗模式消除小部分未消融病变组织区域,避免由于在组织中沉积过多的热量损伤周围健康组织。如图9 及图10 所示,计算了在整个治疗过程结束后由于热量沉积导致组织温升后产生的凝固性坏死区域,在T1、T2、T3辐照模式下,介质在均匀和非均匀分布条件下的靶组织凝固性坏死面积分别为0.759 mm2和1.578 mm2、0.513 mm2和1.145 mm2、1.169 mm2和3.179 mm2,可见即使在相同仿真条件下,介质分布条件的改变对仿真模型预测凝固性坏死面积有较大的影响,因此在构建仿真模型时应充分考虑治疗过程中的组织差异性,提高仿真模型对模拟实际治疗过程的精确性和有效性。
4 结论
本文基于K-wave 仿真工具包构建了聚焦超声换能器辐照浅表组织的三维仿真模型,仿真模型考虑了声传播过程中的非线性效应,研究介质物理属性均匀和非均匀的分布特性对声场和温度场的影响,采用有限元法结合Westervelt 方程求解换能器辐照域内靶组织的声场,得到了换能器辐照区域中声轴面方向基波同谐波声场的分布及沿声轴线方向的声压幅值分布。基于所求得的声场分布结果,通过Pennes 生物传热方程求解温度场,比较了3 种不同辐照模式对温度场变化的影响,并在此基础上预测了换能器辐照域中的靶组织凝固性坏死面积。结果表明,相对于非均匀分布,介质在均匀分布状态下聚焦区域的声压幅值及温升幅度都较小,从而导致在2 种不同介质分布特性下预测的凝固性坏死面积也存在较大差异。此外,仿真模型对换能器激励时间和间歇时间敏感性较高,在较短时间内可使组织上升到所需的治疗温度,选择合适的辐照模式可更好地控制组织凝固性坏死面积。本文建立的仿真模型对声传播过程和治疗过程中温度场的变化进行了研究,为临床医师制定术前治疗计划和选择合适的治疗参数提供了参考。

