工业机器人齿轮传动系统非线性振动研究
巩嘉贝,邢 倩,刘宏达
(石家庄邮电职业技术学院,石家庄 050000)
近年来,随着工业自动化的不断推进,越来越多的自动化设备在各行各业开始涌现,其中工业机器人的使用越来越广泛。而直齿轮传动相较于其他传动形式,有着运动平稳性好,传动精度高,有精确的传动比且传动承载能力强的特点,在工业机器人领域中被广泛使用,具有极大的应用价值。直齿轮在传动过程中,齿面相互接触传递动力,两齿的啮合频率是传动过程中的振动及噪声产生的关键因素,直接影响着传动的效率及质量。因此,深入研究啮合频率对工业机器人直齿轮传动系统的非线性动力学影响十分重要。
目前国内外学者针对齿轮系统的动力学特性等多个领域都进行了相关研究。石照耀等[1]研究了考虑多种非线性因素的不同误差对齿轮振动特性的影响;邹玉静等[2]探究了直齿轮的摩擦润滑对动力学特性的影响;Shen 等[3]基于谐波平衡法分析了圆柱齿轮的包含间隙和时变误差的非线性振动。Atanasovska[4]基于映射法研究了直齿轮传动系统的动力学特性。盛兆华等[5]研究了不同误差对直齿面齿轮传动特性的影响。杨振等[6]建立了直齿面齿轮的多参数非线性振动模型。宋欢等[7]建立单级齿轮动力学模型,对比分析不同方法求解方程的精度,并开发一种改进的Fourier 级数计算方法;张慧博等[8]提出了一种考虑多间隙的齿轮轴系动力学模型,并通过实验进行验证;王奇斌等[9]研究了修形对直齿轮传动系统的动力学影响,并用有限元方法进行对比分析。杜文辉[10]研究了多个自由度的齿轮传动系统的动力学特性,针对事变啮合刚度的变化规律对动力学特性的影响作了详细研究。张婕[11]构建了机车传动系统的多自由度的动力学模型,通过龙格库塔法求解了其多因素对动态特性的影响,并分析了其李雅普诺夫稳定性。向玲等[12]通过集中参数建立风电齿轮传动系统平移-扭转动力学模型,研究了不同支撑刚度对于风电齿轮箱传动系统的非线性动力学特性的影响。
从目前的研究成果来看,在圆柱齿轮及其他齿形齿轮的制造及动态模型等领域研究较多,而针对直齿轮传动中啮合频率对于非线性振动的影响较少涉及。因此,本文基于牛顿第二定律建立了直齿轮传动系统的动力学模型,通过数值方法求解了非线性动力学微分方程组,研究了两齿轮啮合系统频率对整个传动系统的非线性振动规律的影响,为进一步研究工业机器人用不同类型齿轮振动特性提供参考,对提高齿轮传动效率及质量,进一步推进工业机器人的发展,有着极其重要的应用意义。
1 直齿轮传动系统动力学模型
直齿轮传动是由2 个直齿轮啮合传递动力,轴线平行的传动方式,通过集中参数法建立齿轮传动系统的动力学模型如图1 所示。为简化模型,将2 个齿轮分别视为集中质量惯量块,支撑轴视为无质量刚体,轴承为弹性支撑,使用弹簧和阻尼器模拟。
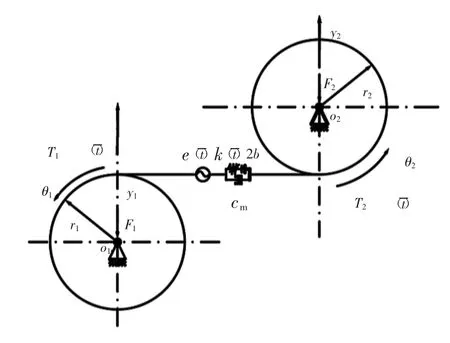
图1 齿轮传动系统的动力学模型
2 直齿轮传动系统动力学模型
在传动过程中,传动系统因误差振动等因素的存在,会在啮合处法线方向产生相对位移λn,表示如下
式中:r1和r2分别为2 个齿轮啮合点到其中心轴线的距离;α 为法面压力角;e(t)为传动误差。在齿轮制造及安装过程中,误差是不可避免的,这些误差激励对齿轮啮合传动影响较大,为了方便研究,通过简谐函数对传递误差进行拟合,表示如下
式中:e0为误差常量,通常取e0=0;er为幅值;ω0为角啮合频率;ϕ 为相位角,一般取ϕ=0。两齿轮间的动态啮合力表示如下
式中:km为平均啮合刚度;cm为振动模型啮合阻尼;f(λn)为间隙函数,可定义为
根据牛顿第二定律,分别对面齿轮传动系统各振动方向列出运动微分方程,则可以得到传动系统的振动方程组为
式中:J1、J2分别2 个圆柱齿轮的转动惯量;cm与km分别为齿轮副的阻尼与支撑刚度;T1为输入扭矩,作用在主动圆柱齿轮;T2为载荷转矩作用在从动齿轮上
3 啮合频率对系统周期和混沌的影响
采用四阶变步长自适应Runge-Kutta 数值积分方法求解面齿轮传动系统运动微分方程,主要参数见表1,依次得到随着系统误差变化的系统响应图。
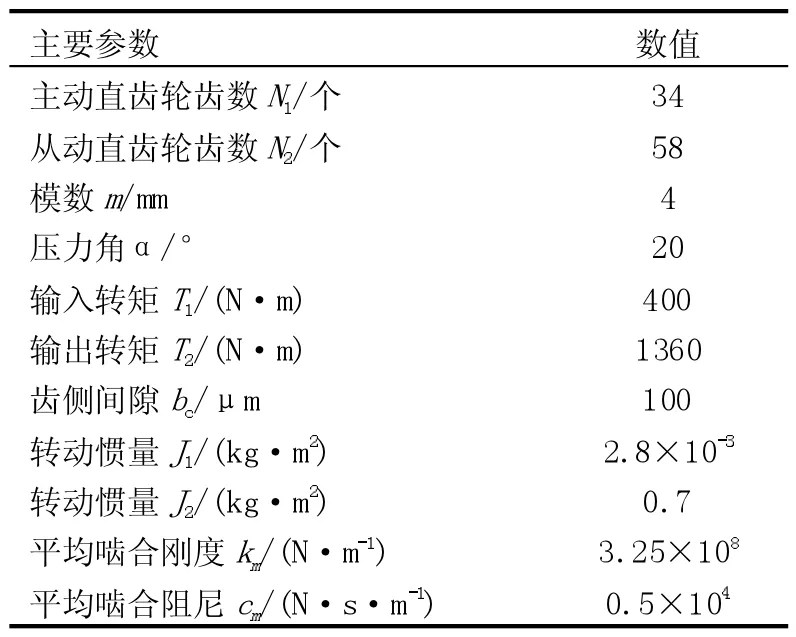
表1 主要参数表
系统响应随着系统频率的增大依次呈现出单周期简谐响应,倍周期次谐响应,混沌响应。当系统响应频率ω=0.1 时,系统呈现单周期简谐振动响应,此时相图为一条闭合曲线,频谱图有一个明显波峰,如图2 所示。
当系统响应频率ω=1.5 时,系统呈现出倍周期次谐振动响应,此时相图为多条闭合曲线,频谱图有3 个明显的波峰,如图3 所示。
当系统响应频率ω=2.7 时,系统开始呈现出混沌周期振动响应,此时相图为多条闭合曲线,相互交叉缠绕,频谱图出现明显不规律波动,时间历程图的波形不稳定,如图4 所示。
由图2、图3 和图4 可得,随着系统频率这一内在激励增大,相图从单周期响应到倍周期次谐周期响应,再进入混沌响应周期。系统的运动轨迹逐渐复杂无规律,平面相图由单条曲线逐渐变成多条曲线相关交叉杂糅,且系统振幅发生变化,在混沌周期频谱图会有不规则振动。在传动过程中,整个系统的振动在一定程度上标志着传动性能的质量,结合系统周期响应图,系统频率处于0~2.6,系统处于简谐周期、倍周期响应,传动性能较好。
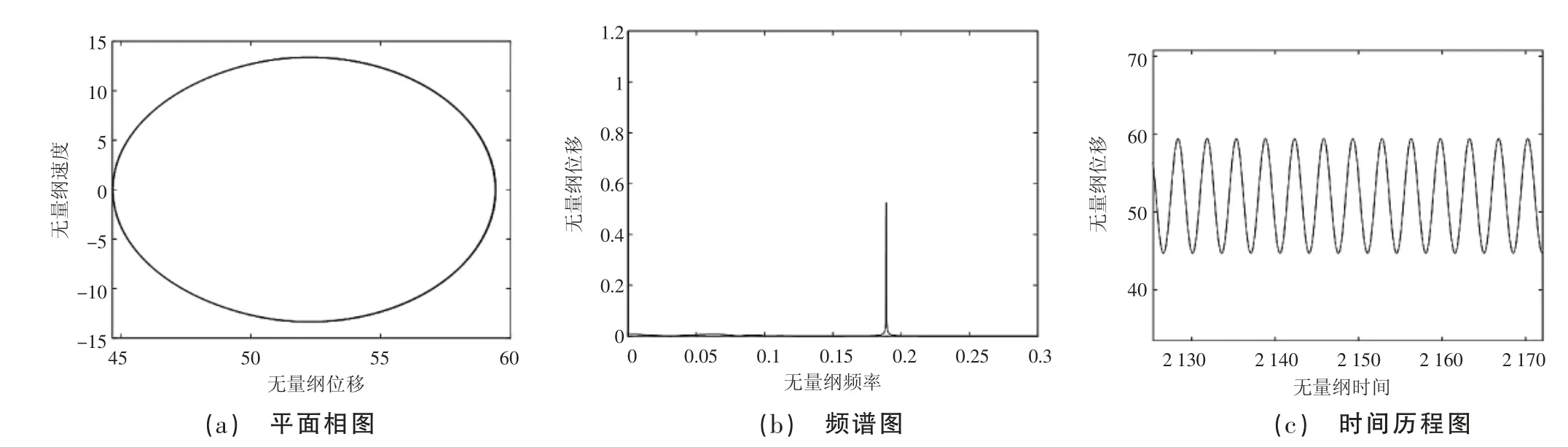
图2 系统频率ω=0.1 时系统单周期响应
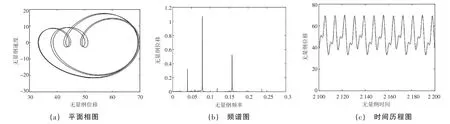
图3 系统频率ω=1.5 时系统倍周期响应
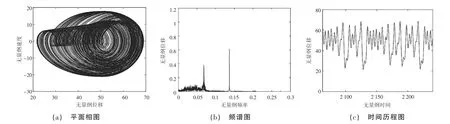
图4 系统频率ω=2.7 时系统混沌周期响应
4 结论
1)本文基于牛顿第二定律,通过集中参数法建立了包含多参数的直齿轮传动系统动力学模型,分析了受力情况,并使用自适应步长龙格库塔法求解微分方程组。
2)研究了随系统频率变化的系统周期响应,以及通过相平面图、频谱图和时间历程图来分析系统的非线性现象。结果表明,系统频率处于0~2.6,系统处于简谐周期、倍周期响应,传动性能较好。
3)工业机器人在推进工业自动化领域扮演着不可缺少的重要角色,其传动的性能与质量关乎这一产业的发展路径,研究非线性振动特性,对提升工业机器人传动质量十分重要。

