一类条件最值问题的快速解法*

福建省龙岩市高级中学 (364000) 李桂英

基本不等式是求解函数最值问题的一个有效工具，不仅是高中数学教学的重点，而且是高考考查的一个热点.然而，学生在应用基本不等式求最值时，往往因为不知如何获取“和为定值”或“积为定值”导致无法运用基本不等式正确求解出最值.而灵活应用已知条件去构造、去变形从而获得“定值”又是此类问题的难点.针对学生不能灵活获取“定值”的实际，笔者在教学实践中，探寻了一种既能降低构造“定值”这个难点，同时又能快速准确求出一类条件最值问题，本文将结合教学实践，例说此类条件最值问题的快速解法.

1 一个重要结论

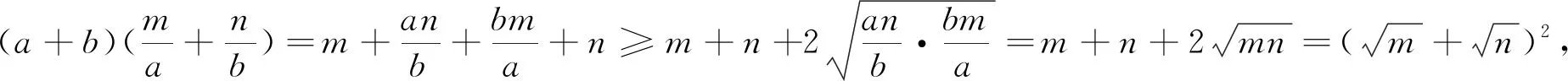
此类条件最值问题的常规解法是通过常值代换后利用基本不等式来求解.若能灵活应用本文定理求解，便可避免常值代换，使此类问题直接快速得到求解.

2 应用

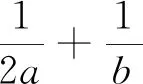
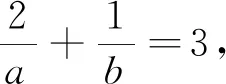
变式4 已知a>0,b>0，且2a+b=3ab，求2a+b的最小值.

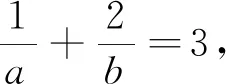
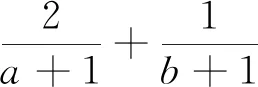
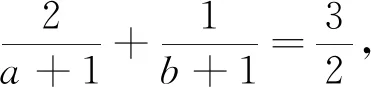
综上可见，引导学生尝试应用本文中所推证的结论去求解一些条件最值问题，不仅能很大程度上降低了构造定值的难度，减少了计算量，从而缩短了学生解决此类问题所耗费的时间，有效地提高了学生解题的准确率，而且能很好地渗透了化归与转化的重要数学思想.并且通过一题多变，多题归一，能加深学生对定理本质的理解与掌握，达到对此类题目的融会贯通.