基于SABA 优化的Volterra 级数空战目标机动轨迹预测
李战武,彭明毓,高春庆,杨爱武,徐安,方诚喆
(1.空军工程大学 航空工程学院,西安 710038;2.空军工程大学 研究生院,西安 710038;3.中国人民解放军 94582 部队,信阳 464194)
近年来,随着空战进程的加快,空战目标的状态预测需求随之愈加迫切,因而信息化战场下,如何通过海量数据进行分析已成为一个热点问题。在空战对抗过程中,飞行员可通过海量的目标状态数据进行挖掘分析,挖掘出目标状态信息中利于作战决策的价值信息,从而及时、有效地获取目标潜在的作战规律,客观地分析、总结敌方的作战方式及特点,进而实现对战场态势的实时感知与获得优势占位[1]。因此,通过空战目标状态数据进行目标机动预测,对飞行员作战决策及获取先敌优势具有重要意义。
目前,目标机动轨迹预测主要有2 类途径。其中,一类的主要思想是利用卡尔曼滤波算法的传统预测思想进行轨迹预测。该方法具备优异的估计能力,对于运动状态变化大且随机性高、运动方式多样的目标轨迹有较强的适用性,因而能够实现目标实时的状态估计与预测,并适用于有限维度的线性和非线性目标时空运动轨迹。例如,姜佰辰等[2]针对目标运动模式变化多及机动幅度较大的情况,提出了一种基于多项式卡尔曼滤波的运动轨迹预测算法;赵帅兵等[3]针对历史位置信息存在缺失的情况,提出了一种具有系统噪声估计的改进卡尔曼滤波算法,对目标机动轨迹进行预测;乔少杰等[4]针对传统轨迹预测算法精度和实时性不足,提出了一种基于卡尔曼滤波的动态轨迹预测算法;翟岱亮等[5]针对高阶目标运动模型存在的高度非线性、数据处理难度大及预测精度低等问题,提出了一种改进的交互多模型轨迹预测算法。上述预测算法都只适用于目标运动特性相对简单的轨迹预测问题,但是在空战过程中,目标的运动往往是高度复杂的时序过程,传统的轨迹预测算法不能准确地学习目标的机动特性,同时也存在建模复杂度高和算法适应性差的问题,并且算法的预测精度难以满足空战对抗需求。
另一类方法主要以智能算法为核心,结合大数据建立目标机动轨迹预测模型。例如,杨彬和贺正洪[6]针对广义回归神经网络(generalized regression neural network, GRNN)模型对非线性数据有较好的预测性能,且容错性及鲁棒性较好,将该预测模型运用于高超声速飞行器的轨迹预测当中;针对BP 神经网络存在对初值敏感且全局搜索能力较差的问题,谭伟[7]和甘旭升[8]等分别利用遗传算法(genetic algorithm, GA)、粒子群算法对预测模型参数进行寻优此外,目标机动轨迹预测的本质是对时间序列数据进行预测,因而具有高度非线性和时变性的特点[9]。理论和实践表明,Volterra泛函级数模型对于非线性系统可以很好的表征,同时对时间序列可以进行精确预测。然而,高阶Volterra泛函级数模型核函数的求解是其应用瓶颈。目前,V olterra泛函级数参数辨识方法有传统的最小二乘法[10-13]及智能启发式优化算法[14-18]。但是,最小二乘法在辨识参数时必须满足目标函数是连续可导的条件,同时搜索时利用梯度信息而容易陷入局部极值。因此,可以采用智能算法克服传统辨识算法的缺点,但传统的智能算法在结构和优化的实时性方面仍存在很多的不足。
蝙蝠算法(bat algorithm, BA)是受蝙蝠回声定位行为启发而提出的一种新型搜索优化算法[19],其模型较为简单,且算法参数少、普适性强。因此,本文将蝙蝠算法引入到Volterra 泛函级数模型的优化中,同时为解决基本蝙蝠算法中存在的易陷入局部最优和求解精度低的问题[20-21],运用变异机制和自适应步长控制机制改进蝙蝠算法,并将其用于优化Volterra 泛函级数模型,构建一种基于改进蝙蝠算法优化的Volterra 泛函级数目标机动轨迹预测模型。通过仿真实验证明,该模型的预测性能优于基于基本蝙蝠算法、粒子群算法、蚁群(ant colony optimization, ACO)算法优化的Volterra 泛函级数模型和反向传播神经网络(back- propagation neural network, BPNN)预测模型,同时也验证了该预测方法的有效性。

1 非线性Volterra 泛函级数模型

式中:ai为 基于 Volterra泛函级数核函数的对称性引入的权系数,并且满足如下关系:

当模型取合适的记忆长度时,在误差允许的范围内,e (k)可忽略不计。
2 改进的蝙蝠算法
2.1 基本蝙蝠算法
蝙蝠算法是Yang[19]在2010 年提出的模拟蝙蝠觅食特征的启发式群智能随机搜索算法。该算法通过模拟蝙蝠在觅食过程中向外发出的一些超声波,根据其特征(包括脉冲频率 f、响度 A及发射率R等)的变化而建立的寻优模型。在算法寻优迭代的过程中,可将蝙蝠个体 i的参数变化描述为
式中:d 为算法此刻正进行的迭代次数;β ∈[0,1]为随机数,且服从均匀分布;v 为速度;x*为算法此时最优的全局解。
在算法的全局最优解附近,应对其进行局部搜索,采取如下策略:
式中:ε为 [-1,1]之 间的随机数;Ad为当前蝙蝠种群的响度平均值。
算法的脉冲响度 A和脉冲发射率 R按照如下策略进行更新:
式中:α为蝙蝠响度的衰减系数;γ为脉冲频率的增加系数。其中,α 和 γ都是常量,同时通过选取合适的 α 和 γ可以有效平衡算法全局搜索及局部搜索的能力。随着算法深入,可以得到
2.2 自适应的改进蝙蝠算法
蝙蝠群体在接近觅食目标时,为不被发现且能够实时监察目标的运动状态,采取提高超声波发射率 R,同时减小脉冲响度 A的策略。因此,基于上述分析可以看出,该算法的寻优能力与脉冲响度 A及脉冲发射率 R的动态变化息息相关。寻优初期,局部极值可能出现多个,此时的脉冲响度 A较大,因而在解空间内应采取更多的全局搜索策略。此时,可将脉冲响度与算法的全局搜索能力相结合,以使算法实现全局搜索能力的自适应调整。寻优后期,算法初步进入极值区域,发射率 R较高,因而应采取更多的局部搜索策略。此时,可将发射率 R与算法的局部寻优能力相结合,以使算法实现更优的局部寻优能力。基于上述分析,基于自适应蝙蝠算法(selfadaptive bat algorithm, SABA)利用自适应步长控制机制和变异机制[20]改进传统的蝙蝠算法。
2.2.1 自适应步长控制机制
对于蝙蝠个体i 的速度更新方式,可借鉴粒子群算法[24]中的速度更新规则方式。在原有的更新机制中,对速度更新加入了惯性权重因子,即
式中:ω为惯性权重因子,其可以影响蝙蝠算法的全局搜索及局部搜索的能力,改进算法参照粒子群算法中的调整策略,采取线性递减的惯性权重方法,算法前期 ω的数值较大,可以使算法具备较强的全局搜索能力,算法后期 ω的数值应选取较小值,使算法在最优解附近具备较强的局部寻优能力,同时加快收敛;h*为 蝙蝠个体的历史最优解;x*为当前蝙蝠种群的最优解;f1和 f2为 脉冲频率;r1和 r2为取值在(0,1)之间的均匀分布的随机数。
通过对改进后的蝙蝠个体速度更新公式分析可以看出,不仅惯性权重对蝙蝠速度更新有影响,同时脉冲频率 f1和 f2也对蝙蝠速度更新有影响。算法初期,选取较大的脉冲频率 f1可以增加群体的多样性,改善全局寻优能力;在算法后期的局部寻优中,选取较小的脉冲频率 f2能够提高算法的局部寻优能力,同时加快收敛。因此,本文提出一种自适应改变脉冲频率的机制,以提高脉冲频率 f1和 f2随算法进程的自适应学习能力,其更新公式如下:
式中:Favg为蝙蝠种群的所有个体适应度的平均值;Fbest为当前迭代次数下蝙蝠种群中的最优个体;脉冲频率 f1在 不同的迭代次数 d中,由不同的适应度平均值 Favg决 定,其2 种影响因素权重分别为 γ 和 α;fmin为脉冲频率最小控制量。
针对算法在局部寻优后期阶段过程中的搜索策略,改进的蝙蝠算法将当前迭代次数 d融入至主要寻优参数脉冲发射率 R与脉冲响度当中。其结合步骤如下:
1)选取一个随机参数 β ∈[0,1]。当 β小于蝙蝠脉冲发射率 R时,算法将进入局部寻优阶段。随着算法进程的不断深入,迭代次数增加,蝙蝠脉冲频率也将增加,从而在算法后期阶段,局部搜索最优解的概率也会增大。

引入分段函数 g(d′)是为了在算法初期具有较大的搜索步长,从而扩大算法的搜索区域;进入算法局部寻优阶段时,调整较小的搜索步长,有利于提升寻优精度。
2.2.2 变异机制
2.2.1 节引入的自适应步长控制机制仅仅能够有效改善算法的全局搜索能力,但不能保证算法一定能够搜索到全局最优解,并且在算法后期,随着脉冲频率 f1的减小,导致算法的全局搜索能力下降,因此算法仍可能陷入局部极值解当中。主要原因是:在基本的蝙蝠算法中,算法后期的个体响度减少为0,发射率增大为1,使得蝙蝠个体无法采取变异操作。因此,对响度 A及 发射率 R进行相关限定约束,使算法后期也可变异操作而不易陷入局部最优。脉冲响度 A和 发射率 R的更新规则为
式中:fmax为最大脉冲频率限制。其中,脉冲频率f1和 f2由当前迭代次数及种群适应度平均共同决定,因此随着算法深入,脉冲响度及发射率产生相应的自适应变化。
结合上述对蝙蝠觅食过程特点的分析,为实现变异操作,本文提出一种结合脉冲响度的变异机制。其变异操作过程如下:对于随机数 β1∈[0,1],如果满足 β1<A条件,同时算法中的蝙蝠个体未进入局部搜索阶段,则继续生成一个随机数 β2∈[0,1];如果随机数 β2满 足条件 β2≥ρ ∈[0,1](ρ为阈值),则对该蝙蝠个体进行随机重置。
上述自适应步长控制机制及变异机制是在全面分析了解蝙蝠觅食行为特征的基础上,充分结合蝙蝠觅食时发出的超声波特征参数,以避免算法过早在寻优过程中寻到局部最优值,同时也提升了后期的最优解求解精度。SABA 算法的具体流程如下[20-21]:

步骤 2 对第 i只蝙蝠个体的位置 xi、速度 vi、发射率 Ri及 响度 Ai分别进行初始化,同时根据目标函数求解第i只蝙蝠个体的适应度值。
步骤 3 根据式(20)和式(21)更新蝙蝠的脉冲频率 f,根据式(26)和式(27)更新蝙蝠的脉冲响度A及 发射率 R。
步骤 4 根据式(19)对蝙蝠个体的速度进行更新,根据式(14)对蝙蝠个体的位置进行更新,依据定义的适应度函数计算蝙蝠个体适应度。
步骤 5 判断蝙蝠个体是否符合进行局部搜索操作的条件。如果符合,则根据式(22)~式(25)转入局部搜索操作,计算蝙蝠个体的适应度,并转到步骤7。
步骤 6 判断蝙蝠个体是否符合变异的条件。如果符合,则对蝙蝠个体采取变异操作,并得到每个蝙蝠个体的适应度值。
步骤 7 判断算法是否达到结束条件。如果未达到,转至步骤3。
3 基于SABA 优化的Volterra 泛函级数模型
Volterra 泛函级数模型是非线性动力学系统中最基本的模型,具有线性和非线性的特性,同时综合线性滤波器、非线性滤波器及预测的功能,因而具备满足系统实时性要求的能力[22-23]。利用截断之后的Volterra 泛函级数模型对目标机动轨迹进行预测的关键在于确定核参数,其辨识精度直接影响目标机动轨迹预测的精度。对Volterra 泛函级数核参数进行辨识实质上是一个多维度参数优化问题,可通过改进后的SABA 算法优化Volterra 泛函级数模型的核参数。
将Volterra 泛函级数核参数作为待优化变量,且将模型输入的轨迹时序数据与核参数向量之间得到乘积值。其中,SABA 算法的适应度函数为其乘积值与真实输出值向量的均方差。SABA 算法通过不断迭代进行寻优的方式,使得预测模型输出不断逼近真实值,从而得到核参数。采用SABA 算法优化Volterra 泛函级数,待优化的核参数向量可以表示为
将核参数向量作为SABA 算法的个体位置,算法搜索空间维度为
式中:F(*) 为 计算预测输出 yˆ和 理想输出 ye的均方误差(MSE);Hˆd为算法第 d次迭代所优化的核参数向量值。
基于SABA 算法优化的 Volterra 泛函级数目标机动轨迹预测流程如图1 所示。
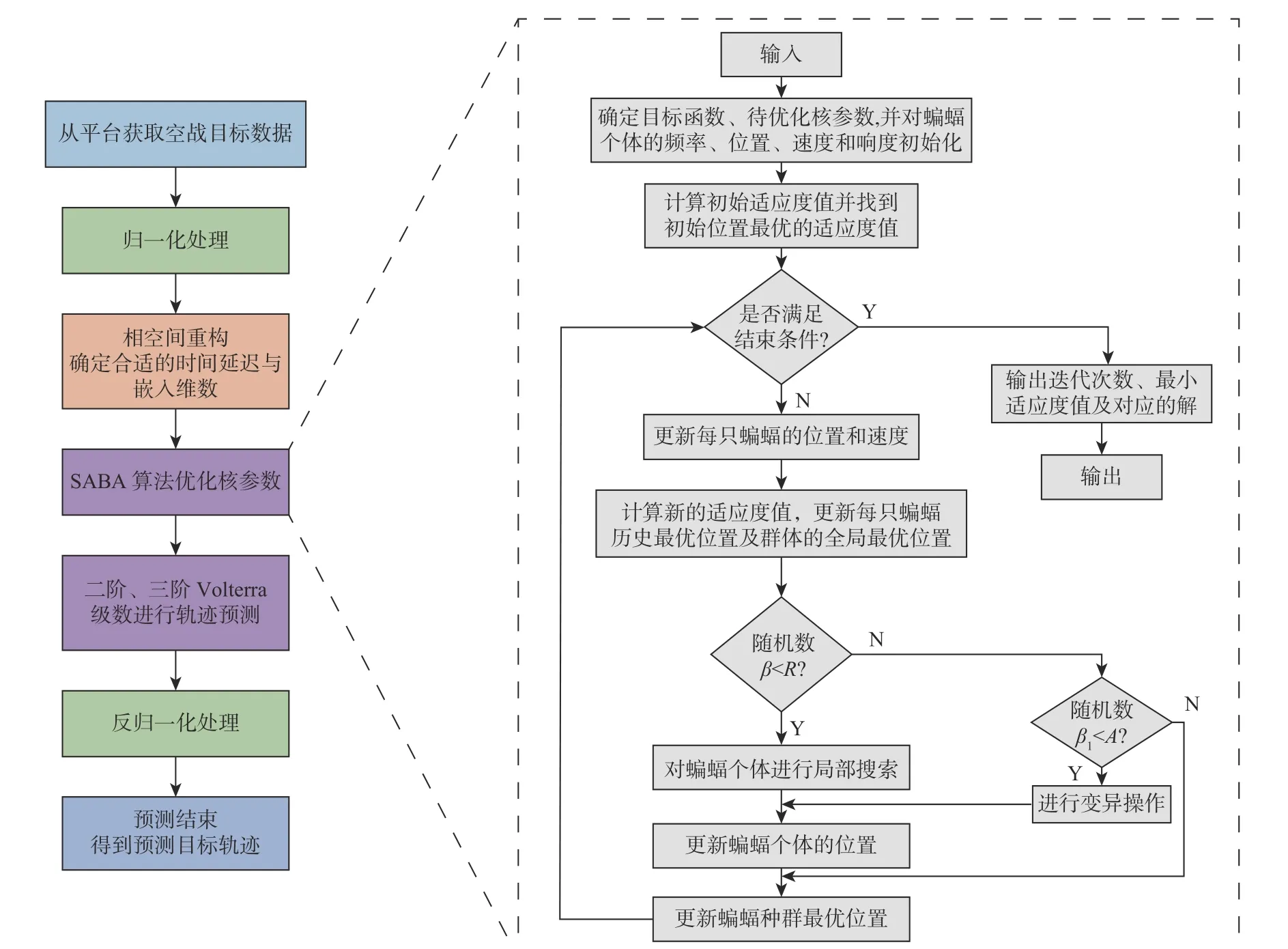
图1 基于SABA 算法优化的Volterra 泛函级数目标机动轨迹预测流程Fig.1 Flow chart of target maneuver trajectory prediction based on Volterra functional series optimized by SABA algorithm
4 仿真实验
4.1 数据预处理
仿真通过基于4 种智能算法优化的 Volterra泛函级数模型进行目标机动轨迹的预测,并进行对比分析。同时,为了更好地发挥预测模型的性能,对目标历史机动轨迹数据进行了归一化和反归一化处理[25]。假设目标历史机动轨迹的原始数据为X=(x1,x2,···,xN),X ∈RN,进行归一化的方法如下:
式中:N为目标历史机动轨迹时间序列的长度;x(t)为 待归一化处理的初始数据;x′(t)∈[0,1]为经过归一化处理之后的轨迹数据;xmax为 原始数据 X中的最大值;xmin为 X中的最小值。
假设基于智能算法优化的 Volterra泛函级数预测模型仿真输出为 Y=(y1,y2,···,yN),Y ∈[0,1],对其进行反归一化的方法为
式中:y(t) 为模型得到的预测值;y′(t)为经过反归一化处理之后的预测轨迹值;ymax为预测得到序列Y 中的最大值;ymin为 预测得到序列 Y中的最小值。
为获得原始数据的相空间结构,可通过相空间重构进行处理[25]。该处理可利用一维时序数据逆向重构出原始系统的相空间结构。Takens 定理[26]证明了在原始的系统中,其任一分量的演化均由其他及其相关的分量确定。假设获得的分量为x,研究的时间序列为 x(t),t=1,2,···,N,则其重构的相空间可表示为
式中:τ为时间延迟;m为嵌入维数。选择合适的时间延迟和嵌入维数可以对未来 t +η时刻的目标机动轨迹值 x(t+η) 进 行预测,其中,η为预测步长。当η=1时 ,即对目标机动轨迹进行单步预测;当η >1时,即对目标机动轨迹进行多步预测。
4.2 目标机动轨迹时间序列预测
仿真采用4 种智能算法优化的 Volterra 模型和BPNN 模型对目标机动轨迹时间序列进行单步预测并分析。首先,对目标机动轨迹时间序列进行相空间重构[26]。根据C-C 法[26]确定目标机动轨迹x方向嵌入维数mx=6和 时间延迟 τx=8;y 方向的时间延迟 τy=7,嵌入维数 my=7;z 方向的时间延迟 τz=5,嵌入维数 mz=7。其中,采用单步预测方式,即设置预测步数η =1。仿真中,采用4 种智能算法优化的二阶和三阶 Volterra模型对目标机动轨迹的三维坐标进行空间位置预测,预测结果经平滑后如图2 所示。

图2 基于二、三阶Volterra 模型目标空间预测结果对比Fig.2 Comparison of target space prediction results based on second-order and third-order Volterra models
通过图2 中预测结果及误差对比可以看出,5 种预测模型的预测值与目标机动轨迹的实际值的变化大体上保持一致,说明4 种智能算法优化的二阶、三阶Volterra 级数模型和BPNN 模型可以对目标机动轨迹进行有效预测。但是从整体上可以看出,基于SABA 算法优化的Volterra 泛函级数模型预测结果较其他模型更加接近真实值,二阶Volterra模型比三阶Volterra 模型更接近真实值,但各个预测模型的预测精度具体效果还需要进行进一步的误差分析仿真实验。
4.3 模型性能评价指标
仿真中,主要对比SABA-Volterra 模型与其他预测模型在预测精度方面的性能差异。仿真实验利用平均绝对误差(Mad)、均方误差(Mse)、平均绝对百分比误差(Mape)及相关系数(Cor)等4 个指标进行衡量对比。其性能指标定义如下:
式中:yˆ(k)为 模型输出的目标轨迹预测值;y(k)为样本中目标轨迹的真实值;y¯ 为 y的 平均值;σ (yˆ) 为 yˆ的标准差;y¯ˆ 为 yˆ 的 平均值;σ(y) 为 y的 标准差;n为样本个数。
限于篇幅,仿真实验以3 个坐标构成三维空间位置精度进行计算分析。其中,空间相关系数取3个坐标预测结果与真实值的相关系数的平均值。
为进一步分析Volterra 泛函级数的预测性能,对SABA-Volterra 算法进行多步预测仿真,并与BAVolterra[27]、SABA-Volterra、ACO-Volterra[16]、GAVolterra、BPNN[7]等预测模型进行对比分析。如表1~表3 所示,分别进行了2、4 和8 步预测。其中,考虑到Volterra 泛函级数的实时性和单步预测的优异性能,采用单步递归方法进行多步预测仿真[28]。即将 t 时刻下得到的单步预测结果 yt与前时序序列 Xt=(xt-m,xt-m+1,···,xt)组合成新的时序序列Xt+1=(xt-m+1,···,xt,yt)作为输入,直至预测所需步数。该多步预测方法对算法的单步预测性能要求更高,以减少多步递归导致的预测误差累积。
通过图2 和表1~表3 可以看出:①基于智能算法优化的Volterra 泛函级数模型,可以利用目标历史机动轨迹数据有效地反映出目标未来运动趋势,并可以较高精度地实现对目标未来轨迹一步预测,且预测结果较为稳定,实现简便、快捷;②基于SABA 优化后的Volterra 泛函级数的单步预测较其他算法优化后的Volterra 及BPNN 预测模型有更高的预测精度,从而实现较优的单步递归方法下的多步预测性能;③基于4 种智能算法优化的二阶Volterra泛函级数模型具有运算速度快、预测精度高的优点,且硬件容易实现。

表1 不同预测模型进行2 步预测的性能对比Table 1 Performance comparison of two-step prediction with different prediction models
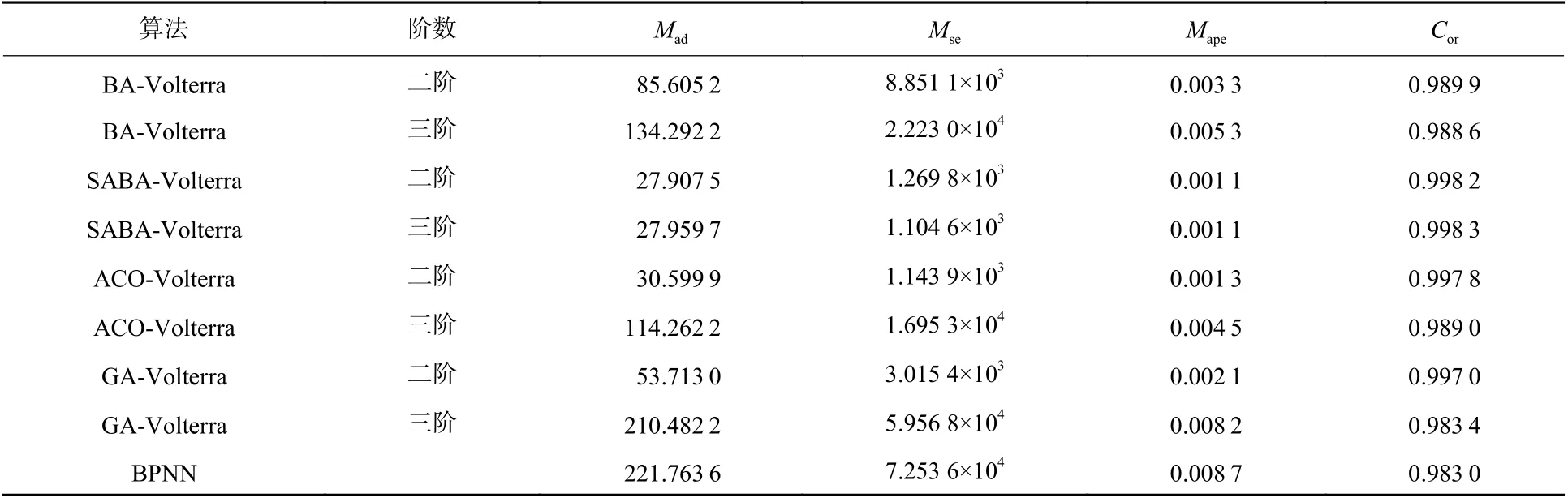
表2 不同预测模型进行4 步预测的性能对比Table 2 Performance comparison of four-step prediction with different prediction models

表3 不同预测模型进行8 步预测的性能对比Table 3 Performance comparison of eight-step prediction with different prediction models
对于目标机动轨迹时间序列,二阶Volterra 泛函级数模型能够对其进行有效预测的本质在于:二阶截断Volterra 泛函级数综合了目标机动轨迹时间序列中的线性和非线性因素,更符合系统的非线性本质[29];而当Volterra 泛函级数的截断阶数取值较大时,其导致存在大量的非线性耦合,而使得Volterra泛函级数模型的系数数量呈几何级数增长,不仅确定模型参数困难,而且非线性项会造成智能算法优化的Volterra 泛函级数参数不佳,进而造成Volterra泛函级数的系数不收敛或者不稳定[30],最终影响预测精度。
4.4 算法优化性能对比
对目标机动轨迹的三维坐标分别进行建模与预测时,GA-Volterra 算法、ACO-Volterra 算法、BAVolterra 算法及SABA-Volterra 算法的收敛曲线如图3 所示。其中,纵坐标为对数坐标轴,且设定为各预测算法在空间位置中寻优适应度的对数值。

图3 不同智能算法优化预测模型的空间适应度函数值比较Fig.3 Comparison of spatial fitness function values of prediction models optimized by different intelligent algorithms
在图3(a)中,二阶情况下ACO-Volterra、BAVolterra、GA-Volterra 和SABA-Volterra 算法的适应度函数值达到较小值且稳定时的迭代次数分别为149、74、230、60;在图3(b)中,三阶情况下4 种算法的适应度函数值达到较小值且稳定时,其所迭代的次数分别为47、63、199、169。仿真中,将Volterra泛函级数的预测误差设定为智能优化算法的适应度函数,即适应度函数值越大,Volterra 泛函级数的预测误差越大。通过上述分析可知,本文提出的SABAVolterra 算法模型能够实现较高的预测精度及较快的收敛速度,同时也进一步验证了二阶Volterra 更加适合于空战目标机动轨迹预测。
4.5 算法实时性能对比
考虑到空战对抗中对预测的实时性要求高,进一步分析SABA-Volterra 模型的实时性能,并与其他算法进行对比。各算法的训练及预测所需时间如图4 所示。其中,迭代次数设置为250 次。
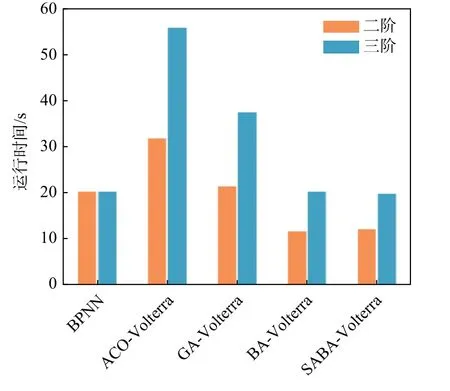
图4 不同智能算法优化预测模型的运行时间对比Fig.4 Comparison of running time of prediction models optimized by several intelligent algorithms
如图4 所示,改进后的SABA-Volterra 级数仍保持较高的实时性,并优于其他传统算法。同时,采取二阶的Volterra 泛函级数模型,相比于三阶能实现更高的实时性。这是由于三阶Volterra 模型需要更多的核函数,从而提高了算法运算的复杂度。因此,综合预测精度与实时性对比,二阶模型相比三阶模型更适用于空战目标机动轨迹预测。
5 结 论
针对空战目标机动轨迹预测问题,引入Volterra泛函级数模型,针对其存在的不足,提出一种改进的蝙蝠算法对其优化,构建一种基于SABA 算法优化的Volterra 泛函级数目标机动轨迹预测模型。通过理论分析和仿真实验可以得出如下结论:
1)改进后的SABA 算法具有自适应步长控制机制和变异机制等能力,可适应不同问题的解空间,从而能够自适应调整合适的步长,进而提高算法求解精度。仿真结果表明,SABA 算法的寻优性能较优异。
2)改进的蝙蝠算法能够确定合适的Volterra泛函级数核系数,所构建的基于SABA 优化的Volterra泛函级数模型能对目标机动轨迹实现较高精度的实时预测。
3)不同的Volterra 泛函级数模型具有不同的预测精度。针对不同的预测问题,需要通过仿真实验,得出最佳的截断阶数。

