浅谈信息技术对初中数学动态问题教学的优化

吴文敏

初中数学教学中，“图形与几何”作为主要教学内容，需要培养学生的空间想象能力与分析能力，提升学生的分类讨论思想与数形结合思想。在此以初中数学动态问题教学为例，教师利用信息技术手段辅助教学，能够帮助学生直观地了解图形变化过程，进而理解题目中各种变量的关系，为几何教学注入新的活力。基于此，本文先讨论在初中数学动态问题教学中运用信息技术的优越性，然后从审题、猜想、验证、实践的角度探究如何将信息技术运用到动态问题教学中，旨在通过此为教师开展解题教学提供参考。

一、初中数学动态问题教学中使用信息技术的优越性

信息技术在解决动态问题的优越性主要体现在：第一，能够更直接地呈现问题中点变化时图像的变化，激发学生的积极思维。在传统动态问题教学中教师只能在黑板上做出静止的图形，精准度还不足，学生难以感受到动态问题中的运用过程，不能感受图形的位置变化，导致在解动态问题的时候容易产生为难情绪，放弃学习。但是在信息技术的使用后，让学生能够加强对图形变化的感知，直观了解位置与数量的关系，减轻学生的解题压力。第二，借助信息技术还能开阔学生的解题思路，培养数学素养。学生在做中考试卷的时候不能借鉴辅助工具，需要在头脑中形成动态思维解答问题，此需要学生掌握一定的动态思维。所以在课堂中运用信息技术开展解题教学，可以让学生在观看的时候主动思考问题，产生跳跃思维，自然地找到解决方法，灵活建构知识。第三，借助信息技术实施解题教学还能提升教学效率。进行动态问题教学时，教师除了讲解问题还要绘图、书写板书，此大大占用了课堂时间，影响教学效率。而信息技术的运用能直接借助多媒体展示图画与板书，减少教师绘画与书写的时间，继而有更多时间深化问题，让学生探究思考，进而能够提升教学效率。

二、初中数学动态问题教学中信息技术的运用策略

（一）借助信息展示动态问题，弄清题意

有时学生受读题能力的影响，在读题后不能有效挖掘条件，或者出现理解错误。特别是当学生面对动态问题的时候，难以有效联想动点、動线、动角等。教师针对此的教学如果使用传统的教学手段，难以让学生了解点或者线的运动过程，当然题目中包含的隐含条件更是难以发现。另外受初中生直观想象能力的影响，还不能将题目中的未知与已知条件结合推敲联想。基于此，学生难以找到数学动态问题的解题途径。

信息技术的运用，能够为学生清晰地展示动态问题，有效挖掘几何动态问题中的隐藏条件，继而找到未知与已知条件之间的关系，找出问题实质。另外如果题目中包含大量的干扰信息阻碍学生解题思路的探究时，在借助信息技术中动态数学技术的时候还能清晰地为学生展示图形中动态元素的变化，加强对问题的理解。

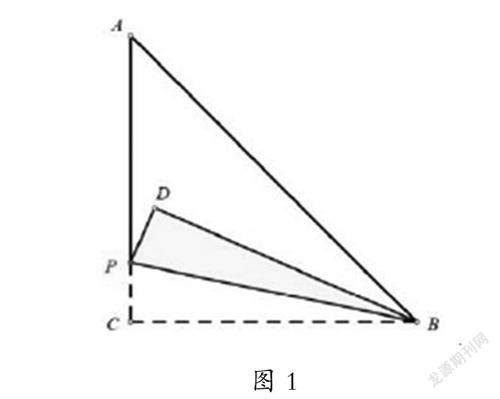
例如问题：如图1，在直角三角形ABC中，∠C=90°，直角边AC与BC相等，为4，点P是直角边AC上的一动点，沿着直线BP折叠三角形BPC，点C的对应点是点D，此时在折叠的过程中点D的路径长是________。此类动态翻折类的问题解答时，需要学生先弄清题意，在传统教学中，教师难以为学生展示随着三角形的折叠点D的变化，单靠学生自己的想象也难以想象出画面。但是借助动态数学技术，则能够清晰地展示三角形折叠的全过程，并能够发现隐含条件，即三角形BPC沿着PB折叠后，△BCP和△DBP一直是全等的，此时PC=PD，BC=BD。

（二）借助信息展示关键信息，助力猜想

初中数学教材中几何知识的呈现是通过严谨的证明得到的，而利用相关知识解答动态问题的时候，我们根据波利亚解题理念要先进行猜想，即在学生找到题目中的已知条件和未知关系以及它们之间的联系后，就可进行合理的猜想。而在传统的动态问题解题教学中，教师使用传统的手段难以帮助学生找出题目中的关键要素，再加上初中生的空间想象能力比较薄弱，所以很难获得正确的猜想过程。所以在解答动态问题教学中，帮助学生找到题目中已知与未知量的内在关系是教学难点。运用动态数学技术能够为学生动态性地展示题目，帮助教师快速解决教学难点。实际教学中，教师可利用信息技术动态数学教学技术中的“跟踪轨迹”功能，对几何图形进行动态化地处理，如此突破学生的动态想象障碍，在几何图形的动态变化下，对题目中的未知建立与已知条件的联系，实施合理的猜想，继而产生解题思路。

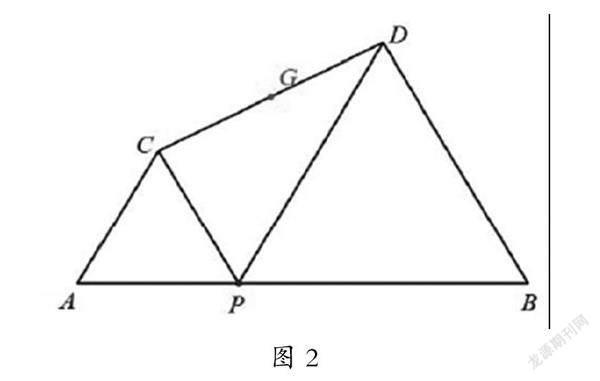
例如问题：如图2，线段AB的长为10，点P是线段AB上的动点，然后以安AP和PB为边分别做△APB和△PBD（△APB和△PBD在线段AB的同侧），连接CD，G是CD的中点，点P从点A出发向点B出发过程中，点G的移动路径长是________。此题中是双动点问题，教师在教授学生“拟定计划”的时候，提出问题：“点P是主动点，点G是从动点，在点P从A向B运动时，点G的运动路径是什么？”请学生先联想思考。然后针对没有想象出来的学生，需要教师再进行引导：“动点G的移动路径跟另一个动点P的路径相同吗？”“你能尝试取几个特殊点吗？”请学生画出草图探究。若还是有的学生不能合理猜想，就可以运用动态数学技术为学生展示动点P的几个特殊位置（与A点重合、与B点重合，在AB的中点上），然后观察点G的运动轨迹是直线。继续提问：“动点的运动轨迹是直线还是圆弧？”此时学生已经可以对自己的猜想有很大的把握，最后在信息技术中动态数学技术的运用下，让学生确更好地猜想点G的运动路径——直线。

（三）借助动态演示解析题目，深化解题

在学生们合理猜想之后，就进入到验证猜想环节中，在此需要找到几何动态问题中的已知与未知的关系。动态问题往往综合性强，让学生难以确定已知数据与未知量的内在联系，特别是在传统的解题教学中，教师难以边讲解边展示图形运动的过程，在此若结合信息技术展示几何图形的动态变化过程，能够帮助学生更深入地理解问题，解题教学达到事半功倍的效果。

例如问题：如图3，平面直角坐标系中有一个矩形OABC，点A和C都在坐标轴上，点B的坐标为（2，），在矩形边BC上分别取点E和F，让三角形CEO沿着OE翻折，再将三角形BFA沿着AF翻折，此时点B落到点G上，得到的三角形为AGF，如果∠OGA=90°。（1）求过点A、O、G的二次函数的解析式与对称轴。（2）二次函数的对称轴上是否存在点P，令△OPG是等腰三角形？在同学们解答完第一小问，确定抛物线的解析式与对称轴之后，在求点P的坐标的时候，教师要先使用动态数学技术中的“隐藏”功能，将△OPG之外的矩形OABC、△AGF和OGE的图形隐藏，让学生直接减少对无关信息的干扰，然后利用动态数学技术中的“绘制”功能，以点O为圆心、G为圆心，OG为半径做圆，圆与抛物线对称轴的点为点P，以此找到点P的坐标。

（四）通过动手操作，积累解题经验

新课程标准要求教师在设计课程的时候融入现代信息技术手段，在解动态问题的时候，还希望学生能够利用信息技术手段有效思考问题，以此优化教与学的方法，让学生能够主动投入到探究性的学习活动中。对学生数学分析能力的培养不是一朝一夕能够完成的，需要循序渐进，让学生逐渐积累数学活动经验，更好地了解数学问题中的包含的规律。所以在解题教学中教师要为学生创造适合的条件，引导其观察、猜测、推理与解答，丰富数学活动经验。

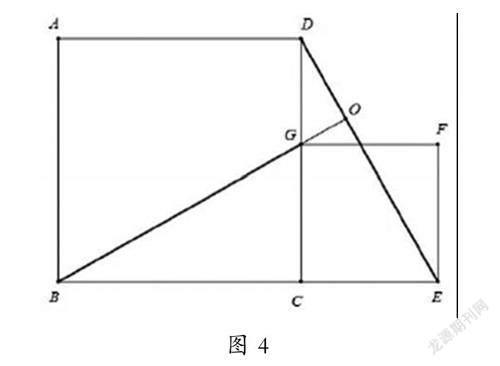
例如问题：如图4，点G是正方形ABCD中CD边上的动点，以CD为边做正方形CGFE，连接DE与BG，求线段DE与BG的关系？在学生们解答完问题后，对此类问题产生了初步认知，教师再设计变式题继续帮助学生巩固知识，请学生自主操作，积累解题经验。变式一，将原题中的正方形CGFE围绕点C旋转一定角度后，请问原题中的线段DE和BG的关系还存在吗？变式二，原题中的正方形变为矩形，两个矩形边的关系为：AB=x，BC=y；EC=kx，CG=ky（x和b≠0，k>0），然后提问线段DE与BG的关系？矩形CGFE围绕点C旋转一定角度后，请问原题中的线段DE和BG的关系还存在吗？请学生利用动态数学技术改变题目条件，自主实践探究，找到问题的答案。

三、初中数学动态问题教学中信息技术的运用实践

以图形旋转类问题为例，问题为：点G是正方形ABCD中CD边上的动点，以CD为边做正方形CGFE，连接DE与BG，求线段DE与BG的关系？教学过程为：第一，借助信息技术手段帮助学生弄清题意。使用动态数学技术，在图4的基础上，设置点G为CD上的动点，使用“变量尺”功能控制点G的位置，让其能够在线段CD上运动，请学生观察，辅助其理解问题。第二，引导学生进行合情猜想。在学生审题之后，发现不能直接利用已知条件求出线段DE与BG的关系。在此教师要引导学生先猜想线段BG和DE的长度与位置关系，受其空间想象能力的影响，运用线段动态数学技术让学生观察，如将图中的线段BG和DE变蓝加粗，然后延长线段BG与DE相交于點O，然后拖动点G，观察随着点G 的变化，两条线段长度的变化、∠BOD的大小变化，如此获得猜想。第三，动态演示深入理解。结合问题中的条件，引导学生尝试证明刚刚的猜想。先证明猜想BG=DE，即证明它们所在的三角形GCB和ECD全等，根据三角形全等的性质得到BG=DE。再证明猜想BG⊥DE，可以制作辅助线DE’⊥DE与AB相交于点E’，然后证明DE’∥BG，继而推导出DE⊥BG。很多学生因为不能想到做这个辅助线，此时教师可以运用几何画板为学生演示三角形CDE绕点D逆时针旋转90°的动画，最后点A和点C重合，点E落到线段AB上直接与E’重合，以此能够加强学生的理解，并指导为什么制作辅助线DE’。

通过在初中动态问题教学中运用信息技术策略的研究，讨论动态问题教学的优化路径，可以有效提升动态问题教学效果，为提升教师教学质量提供可行参考。同时通过信息技术的运用还能帮助学生提升解题能力，建立积极的数学学习情感态度，为培养学生的数学核心素养提供参考。