“拓”材有形 “展”智无痕

刘翠玲

2022版新课程标准提出：数学课程要培养学生“会用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界”，使学生了解数学的价值，欣赏数学美，提高学习数学的兴趣，建立学好数学的信心，形成质疑问难、勇于探索的科学精神。随着新课标的落地，我们越来越深刻地认识到教学应该从“知识本位”转变为“素养本位”。“生本课堂”理念下教师要积极探索发展学生核心素养的路径，不应局限于“教教材”，而是要根据学生实际需要灵活地处理教材，对知识内容、技能、方法进行结构化整合与拓展，通过增加学习内容的文化性、趣味性、挑战性，满足学生的求知欲，使学生面对实际问题时，能主动尝试着从数学的角度运用所学知识和方法寻求解决问题的策略。

下面，以笔者自主开发设计的一节拓展课《画图策略》为例，谈谈新课标理念下小学数学拓展课教学的思考：

解决问题的方法和策略有很多，画图策略是其中之一，它是学生根据所揭示的数学问题内涵，采用画图的方法，把抽象问题详尽化、直观化，从而达到解决问题之目标。画图策略是“数形结合”思想的详尽体现，也是最贴合小学生形象思维特点的有效策略。人教版和苏教版等教材将解决问题的策略作为一个专项学习的内容设置于教材之中，而北师版教材则把画图策略渗透到各个知识点的教学过程中，从一年级开始，就不断渗透数形结合的思想帮助学生理解并内化知识。在具体教学过程中，发现画图作为数学学习的重要“脚手架”，但学生主动运用的意识却极为薄弱，很多学生借助画图解决问题的习惯仅仅是因为“老师要我画而画”，而非是“我要画”的主动意识。为了化被动为主动，让学生对画图的价值有更深刻、直接的体验，现以画图策略为主题进行拓展课的开发和设计，并在北师版的课堂中进行拓展教学，带领学生通过画图的价值体验、策略形成、内化运用等三方面，探寻画图策略在日常数学学习过程中的应用，激发学生自主作图的意识，提高学生的解题能力。

一、策略形成前——“意会”与“言传”触发

“深有体会”与“深度认同”是策略接收和内化的源动力。因此，激发主动性和内驱力成了策略意识培养的首要之举。拓展课的内容作为数学基础内容的有益补充，其内容取向基于教材而高于教材，基于学生而发展学生。因此在内容的选择上，应该结合学生实际去寻找数学核心素养的原始生长点，基于学情实际还原学生的学习常态，并且通过生生互动而自发引起生生触动。

示例1：实验小学种植园有一块长方形菜地，长10米。在整修重建时，菜地长增加3米，这样菜地的面积就增加了18平方米。原来菜地的面积是多少平方米？

1. 互动中感知——化“繁杂”为“简洁”

以纯文字表述的形式出示的例题是我们常见的习题呈现方式。在学生自主尝试解答过程中，发现学情不同解题方式也不同，大致有如下两种：一种是根据题意直接列式解答；另一种是根据题意画出示意图再解答。先让画图的学生说明意图：题中的条件比较多，对文字的阅读理解比较困难，对题中数量关系的理解有些模糊，从而产生用更简洁快速的方法表达题意的需求。画图的策略不在于教师提出的要求，而是学生基于实际需求而自主萌生的。其余学生在对比辨析中体会画图的必要性、简洁性和直观性，领略画图策略对于整理信息所起到的化繁为简的作用。以学生带动学生，以互动引发触动，学生在画图解题的过程中，逐步把抽象的文字转化为形象的圖形，把形式化的数据变成具象化的图像，从而更好地理解已知条件和所求问题之间的联系，图形之妙不言而喻。

2. 解析中感悟——化“抽象”为“形象”

在解题过程中，学生自主结合图形讲解思考过程，充分利用图形直观地分析数量之间的关系，题中“增加部分的长就是原来长方形的宽”这一关键信息在图形解析下一目了然，通过把列式计算转化为图形分析，形成解决问题的思路，有效实现数形结合，发挥了形象思维和抽象思维的协同作用。在变“抽象”为“形象”之间，“意会”与“言传”之中体会画图策略之巧妙。

二、策略形成时——“体验”与“感悟”并举

“数学中的画图和推理，归根结底都是计算。”“推理是抽象的计算，计算是具体的推理，图形是推理和计算的直观模型。”在学生解决问题的过程中，画图不是最终目的，画图只是一种中介，画图是为了更好地辅助思维。充分利用“图形”这种形象直观的表达方式，让其成为学生学习路上的“脚手架”则意义非凡。

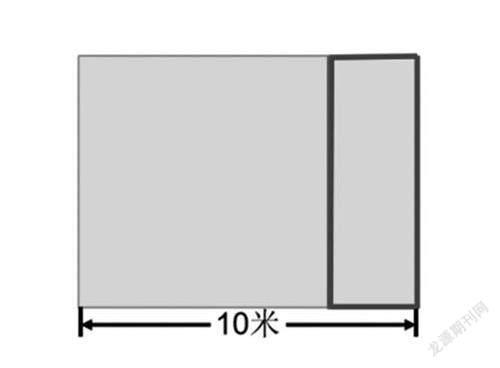
示例2：学校种植园菜地长10米，划分出一个最大的正方形种白萝卜，剩下的部分要用篱笆围起来，求篱笆的长度是多少米？

1. 实践中萌发——有感而“画”

图形与几何领域的知识相对较为抽象，画图策略的作用尤其凸显。例2是长方形周长知识的灵活应用，这个问题不同于一般的简单实际问题，虽然题干简洁却很抽象，学生自主解题的过程中经过例1的启发而自觉使用画图策略的同学已达90%左右，学生自觉借助画图帮助理解题意，由此可见自主意识已被唤醒。

2. 转化中明理——化难为易

仅仅会借助图形整理信息还无法体现画图的价值，图形除了能够帮助整理题中信息理解题意以外，更重要的是帮助解题。这道题要求学生摒弃固化思维——依赖长方形的周长计算公式解决问题，要运用转化的思想——“一长一宽的和=原长方形的长”来解决问题。

为了更好地凸显“生本课堂”，建立基于学生立场的“简教深学”的课堂新样态。在课堂中教师留足时间和空间先让学生自主探究，再借力小组合作探究，尝试解决问题。交流过程中发现不同思维水平的学生呈现了三种不同的生成：

生1：无法解答——这道题信息不完整，没有告诉我们宽是多少，所以没法解答；

生2：假设法——假设划分的正方形边长是9米，因此剩余的长方形的宽是1米，（9+1）×2=20（米）；

生3：转化法——不论原来长方形的宽是多少，剩余的长方形一长一宽的和=原来长方形的长=10米，因此篱笆的长是10×2=20（米）；

可见会画图的同学占大部分，会读图且用图的却不多，大部分学生不懂利用图形挖掘文字层面看不到的隐藏的信息。在集体交流时，第2位学生的假设法受到部分同学的反驳和质疑——如果正方形的边长是9.9呢？由此可见这样的方法只是特例，不够有说服力。而第3位同学结合正方形四条边都相等的特点，带领同学借助图形观察、分析、转化、推理，最终发现：“不管原来长方形的宽是多少，剩下图形的一长一宽的和始终都是10米。”依图形助力，在观察中转化，转化中推理，推理中解题，学生豁然开朗，图形的价值不言自明。

教学过程中， 从“会画图”到“会用图”，生生互动中“寓理于形”，学生感悟到画图策略能把原本隐藏的关系更加形象明了地显示出来，画图不仅化繁为简，还能化难为易。充分凸显学科实践的意义，学生在“深有体验”与“深刻感悟”之中感受到策略价值，策略意识的根植水到渠成。

三、策略形成后——“思考”与“内化”并进

学习不是一蹴而就的，学生学习“解决问题的策略”也不是“一步到位”，而是在步步思索、层层体验中理解和掌握的。因此，教师突破思维固守的“画图”仅适用于“图形与几何”领域的错误认知，不断开拓策略运用的时空领域，通过回顾与分析、变式与对比、感悟与体验等渠道，拓宽知识面，让学生在不同领域中感受策略价值，在不断丰富认知的过程中内化和提升，使学生对“画图”策略达到深刻理解、深度掌握和自发运用的水平。

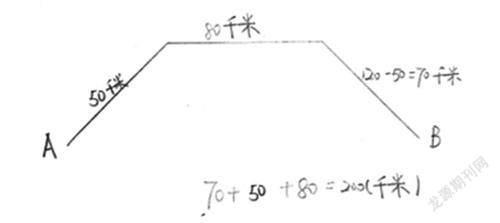
示例3：从A镇到B镇，其中上坡路有50千米，平路80千米，其余的是下坡路，一辆车从A镇到B镇，往返走一趟，共走了120千米上坡路，从A镇到B镇相距多少千米？

1. 领域拓展——“图”尽其用

将画图的策略由图形领域延伸到生活中的其它领域，打破思维局限，引发学生的认知冲突——并不是只有解决图形问题才需要画图，在其它领域中图形的作用一样凸显，帮助学生实现不同领域的跨越，实现知识点的沟通与联系，让学生充分体验画图策略的广泛运用的价值所在。解题过程中，学生借助图形分析，发现去时的下坡路在返回时则成了上坡路，因此，“上坡路共120千米”这内隐的条件便直观地外显出来，用图说话，以图解意。

2. 内化策略——“图”说精彩

以图助力，难点破解，整道题迎刃而解：根据“120米上坡路”而推理得出返回时的上坡路为120-50=70千米，故而两地的三段距离都清清楚楚；还有些思维水平较高的同学根据图意直接用“120+80=200千米”解決问题，原本抽象的题，变得简单明了。以图为具，“图”若画开，策略自来。

课时有限，内容有限，但带给学生的体验和感悟却是无限的。随着学习的深入，虽然学生所遇到问题的类型在不断变换，而解决这些不同类型问题的策略却始终如一，学生对画图策略的感悟和运用越来越娴熟，对策略的理解也越来越深刻，从而“数形结合”“变与不变”“化归”等重要的数学思想便在无形中渗透进而内化为学生的素养。解决问题教学并不是单纯地在“解决问题”，而是解决学生思维方面的“问题”：让学生学会在错综复杂的事物中把握本质，进而提升抽象能力；会在杂乱无章的事物中理清头绪，进而培养推理能力；会在千头万绪的事物中发现规律，进而增强建模能力。这样的课，才是灵动的、生长的，才是根本的、智慧的，才是我们的课堂追求。

新课标理念下，我们要基于单元整体视角建构知识体系，对新授课的课时进行必要的整合和提升，并在必要的教学中引入一些拓展性内容，如以核心知识点为主题的拓展、以开放的习题为主题的拓展、以数学阅读内容为主题的拓展、以数学益智游戏、数学趣题名题难题的拓展等等，让丰富性、多样性、探究性的学习内容为学生的数学学习注入新的活力，注重引导学生在动手操作、实践探索等活动中发现知识，感受数学学习的趣味性，享受探究的乐趣，领略数学的魅力所在，全面提升他们的观察、分析、判断、想象、创造等各方面的能力，从而提升学生的数学素养。

“拓”教有形，“展”智无痕。数学教学并不仅仅是知识的教学，更是智慧教学，学生的学习不是简单的获取知识，而是在获取知识的过程中发展思维能力，提高解决问题的能力。让我们带着学生在有限的时间里畅游魅力无限的数学海洋，从“有知识的人”走向“有智慧的人”。

*本文系泉州市教育科学“十四五”规划（第一批）课题《小学中年级数学拓展课的开发与设计》（编号：QG1451-055）的研究成果。