煤油液滴直径对两相旋转爆轰发动机流场的影响*

杨 帆，姜春雪，王宇辉，李世全，王健平，张国庆

（1.北京化工大学机电工程学院，北京 100029；2.北京大学工学院，北京 100871；3.北京理工大学宇航学院，北京 100081）

爆轰发动机作为传统爆燃推进系统的替代方案，在理论上可以实现发动机整体性能的提高[1-3]。旋转爆轰发动机（rotating detonation engine, RDE）通常使用预爆轰管切向点火，产生一个或多个旋转爆轰波（rotating detonation wave, RDW），爆轰波在接近燃烧室入口处周向传播消耗燃料，产生连续推力[4-8]。对于气相旋转爆轰发动机，已有学者开展了针对其旋转爆轰波的模态跃迁[9-10]、推力性能测量[11-13]、光学测量[14-16]及热测量[17-18]等的实验研究；或通过数值模拟方法研究了几何尺寸[19]，几何结构（如环形[20-22]、空心[23]、圆盘形[24]），燃料和氧化剂喷注方式[25-26]，不同排气喷管[27]等对RDE 流场的影响。而实际上，发动机多使用液态燃料，相比于气相爆轰，气液两相爆轰需要考虑燃料的雾化、液滴的破碎、燃料部分蒸发及燃料与氧化剂不完全混合等过程。液滴燃料的大小、液滴在时间和空间上的分布等参数对气液两相爆轰过程起到了主要作用[28]。

液态煤油作为航空动力的常用燃料，在室温条件下很难与空气发生爆轰。由于燃料液滴必须在形成开始放热所需的自由基之前蒸发，因此部分能量用于蒸发液滴，导致用于驱动爆轰反应的热量较少[29]。实验中通常采用掺氢[30]、富氧[31]、煤油部分汽化[32]等方式来实现旋转爆轰波的传播。由于仅依赖实验难以深入探究RDE 内部流场结构，而对于气液两相旋转爆轰等复杂过程的数值模拟，通常也需要对实验条件进行一定的简化处理。已有研究人员在数值模拟中考虑了液滴的蒸发、雾化过程，对初始液滴采用均匀直径假设[33]和球状假设[34]。煤油本身作为由链烷烃、芳香烃、环烷烃组成的混合物，数值模拟中通常将其视为单一组分平均分子式或代替燃油组分，然后再给定相应的反应机理。

以往的文献中，涉及RDE 流场中液滴分布的分析较少，气液两相RDE 的流场研究有待进一步开展。此外，大多数描述液滴破碎的模型理论都是基于无限范围的均匀气流中的单个液滴，研究表明，喷雾液滴的破碎时间可能是孤立液滴的55%～90%，这取决于液滴间距、直径和流量[35]。泰勒类比破碎（Taylor analogue breakup, TAB）模型由内燃机雾化燃烧过程发展而来，除了应用于低速流动和雾化燃烧[36-38]外，在涉及激波液滴相互作用的超声速流动中也有广泛应用[39-40]。由于气液两相介质的爆轰效果取决于液滴的破碎程度和液滴的尺寸分布，而液滴破碎的程度决定了冲击波后化学能的释放速度[41]。因此，液滴的大小必然对气液两相介质的爆轰参数产生很大的影响。

本文中，以液态煤油C12H23为燃料，高温空气为氧化剂，考虑液滴的雾化破碎、蒸发过程，忽略复杂的燃料裂解过程，采用单步总包反应机理研究旋转爆轰流场，采用成熟的泰勒类比破碎（TAB）模型模拟液滴的雾化破碎过程，以期揭示气液两相RDE 的基本流场结构，分析液滴运动，并比较不同初始液滴直径对RDE 流场的影响。

1 研究方案

1.1 数学模型

旋转爆轰流场区域存在气相和液相两相流动。Fluent 软件中模拟多相流的模型可以分为欧拉-欧拉多相流模型和欧拉-拉格朗日多相流模型，前者的连续相和离散相均采用欧拉法进行求解，后者的离散相则采用拉格朗日法计算。其中，欧拉多相流模型包括VOF（volume of fluid）模型、混合（mixture）模型和欧拉（Euler）模型。对于离散相体积率超过10%的液滴流动，可选用欧拉多相流模型中的混合模型或者欧拉模型；对于体积分数小于10%的液滴流动，可选用离散相模型（discrete phase model, DPM）。

1.1.1 气相控制方程

气相满足连续方程、动量方程、能量守恒方程和组分方程[42]：

式中：ρ 为流体密度，U为流体的速度矢量，u和v为速度矢量U的2 个分量，Γ 为质量源项，µ为动力黏度，p为压力，Su和Sv为动量方程的广义源项，e为比内能，λ 为流体的导热系数，Φ 为黏性耗散函数，Sin为内热源，ωi为组分i的质量分数，Γi为组分i的质量扩散系数，Ri为单位时间单位体积因化学反应和液滴蒸发产生的质量。

1.1.2 离散相控制方程

在拉格朗日坐标系下，由牛顿运动定律得出液滴运动方程[43]：

式中：up为液滴的速度，ρp为液滴密度，dp为液滴直径，Re为相对雷诺数，cd为阻力系数，g为重力加速度，F为液滴其他作用力。忽略重力。当液滴周围流体的密度远小于液滴密度时，可不考虑虚拟质量力。本文中，液态煤油密度为780 kg/m3，空气密度为1.225 kg/m3，空气密度远小于液态煤油密度，因此不考虑虚拟质量力。

通常，在计算液滴运动阻力时采用球形假设，液滴阻力系数（cd,sphere）的计算公式[43]可以表示为：

考虑到RDE 流动中球形液滴在高速气流作用力下将会产生变形，液滴形状的变化决定了需要动态计算阻力系数，表示为[43]：

式中：y为液滴变形因子。

基于液滴震荡、扭曲与弹簧质量系统的比拟，求解控制液滴震荡变形的模型方程组[44]：

式中：m为液滴的质量，x为液滴平衡位置径向变化量，Fg为气动力，ρg和ρl为气相和液相的密度，d为阻尼系数，k为弹性系数，vr为液滴与气体的相对速度大小，r为液滴半径，σ 和µl分别为液滴表面张力系数和黏性系数[42]，无量纲常数cF=1/3，ck=8，cd=5，cb=1/2。

通过求解模型方程组，可以确定液滴的震荡变形，液滴震荡增长到临界值时，母液滴将会分裂出许多更小的子液滴。联合式(12)～(16)，可以得出：

当y=0 时，将按照球形公式计算液滴的阻力；y=1 时，对应液滴临界变形量；y＞1 时，液滴破碎，式(17)由TAB 模型得出。

液滴蒸发过程中，质量守恒方程[44]为：

式中：H为液滴单位面积的蒸发质量速率。

1.2 化学反应模型

化学反应模型为一步反应的层流有限速率模型：

该模型忽略湍流脉动对化学反应的影响。采用Arrhenius 公式计算反应速率[45]：

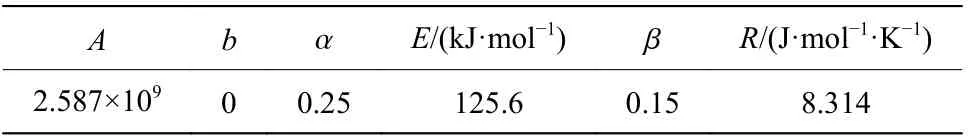
表1 反应速率计算参数[46]Table 1 Parameters used to calculate the reaction rate[46]

1.3 物理模型建立及边界条件

将环形RDE 结构展开为二维以降低计算成本，工作原理如图1 所示。液态燃料爆轰燃烧反应流场涉及到燃料破碎、剥离、蒸发、扩散、化学反应、相变、湍流两相流、激波等复杂物理化学过程。求解过程参数多、计算量大、收敛难度大，网格质量的好坏直接影响计算收敛。本文中，采用均匀四边形网格来保证网格质量。模型X方向长度为0.11 m，Y方向长度为0.10 m。虚线框设置为3 000 K、2 MPa 高温高压点火区，点火区初始X方向速度为2 000 m/s。左、右边界在爆轰波传播第一周时设置为壁面，抑制反向爆轰波的产生。当爆轰波传播至邻近右边界时，将左右边界修改为周期性边界。压力出口边界的背压为0.1 MPa，总温为300 K。空气质量流入口的总温为1 000 K。空气入口采用离散相表面注入方式注入煤油液滴。不同工况的煤油参数如表2所示。

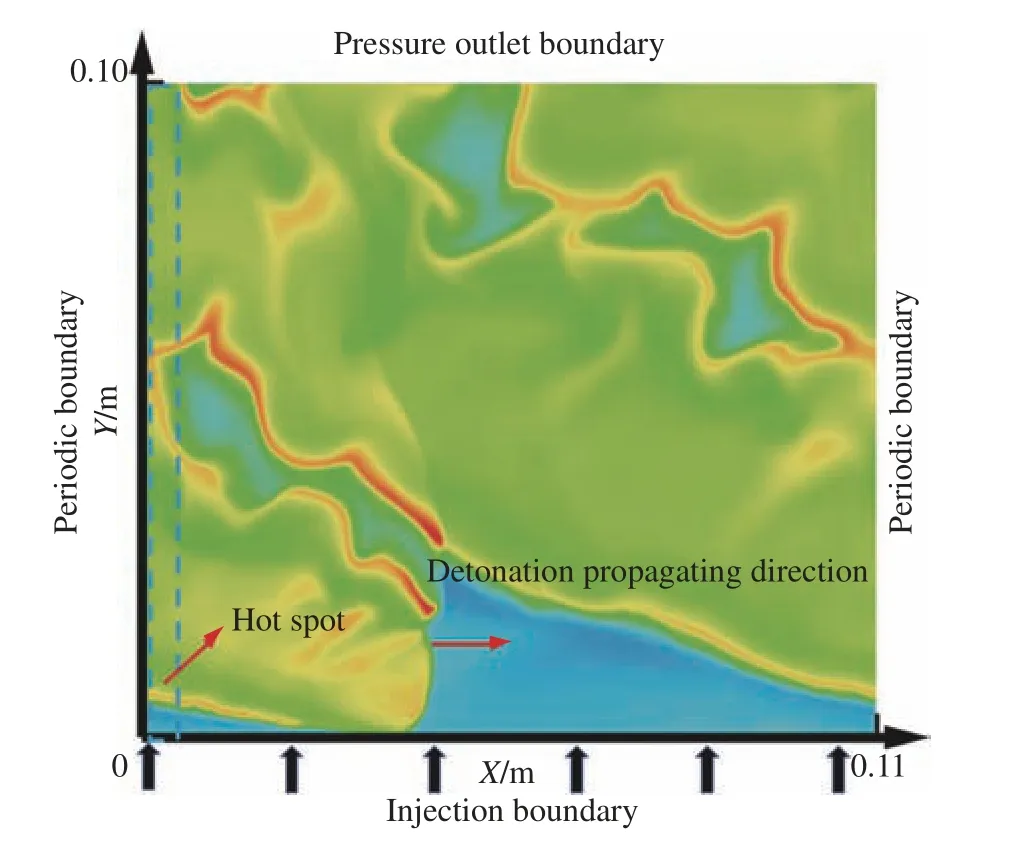
图1 旋转爆轰发动机工作原理Fig.1 Operating principle of a RDE

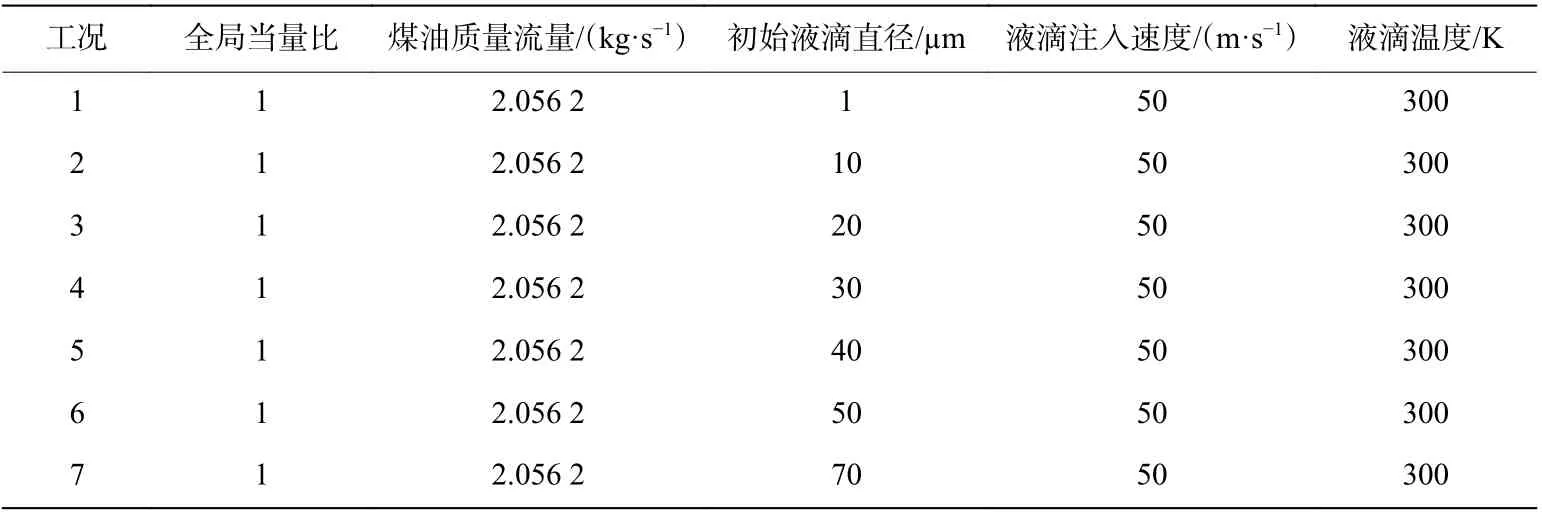
表2 煤油液滴注入参数Table 2 Injection parameters of kerosene droplets

1.4 模型与网格有效性验证

根据离散相与空气的质量流量和密度估算出离散相的体积分数为0.011%，远小于10%，因此采用DPM 模型。初始液滴粒径为30 µm 时RDE 流场的离散相体积分数等值线分布如图2所示。图中离散相的体积分数最大为0.05%，验证了模型的合理性。

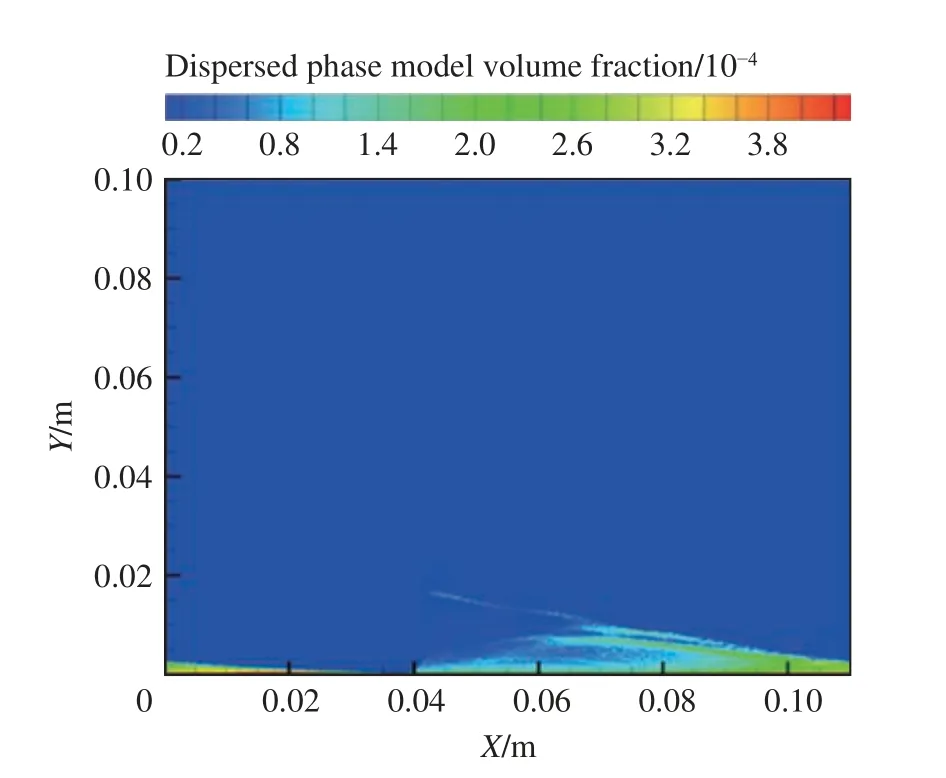
图2 初始直径为30 µm 的DPM 体积分数等值线分布Fig.2 Contours of DPM volume fraction at an initial diameter of 30 µm

真实的喷雾计算中可能有百万液滴，众多液滴轨迹计算成本高昂。两相RDE 模拟中引入了粒子包裹的概念，粒子包裹由单个液滴参数表征，用以减小计算量。而网格尺寸影响单次注入的包裹数目，单次注入包裹的数量等于注入边界的网格单元数量。单次注入的每个包裹所包含的液滴数量为：

式中：N为单个包裹的液滴数量，m˙s为液滴流的质量流量，n为注入边界网格单元数量，Δt为液滴时间步。为了保证一定的计算精度，注入的每个包裹所包含的液滴数量不能太多，Δt设置为1 µs。

选取合适的网格尺寸可以合理地控制流场中的包裹数目。对初始直径为30 µm 的工况，分别在均匀网格尺寸0.20、0.25、0.40 和0.50 mm 下进行计算。图3 给出了不同网格尺寸下RDE 流场稳定后的温度等值线。从图3 可以看出，爆轰波、斜激波、缓燃接触面均可捕捉，但在0.20 和0.25 mm 网格尺寸下，可以更清晰地捕捉到接触间断附近的低温条带。

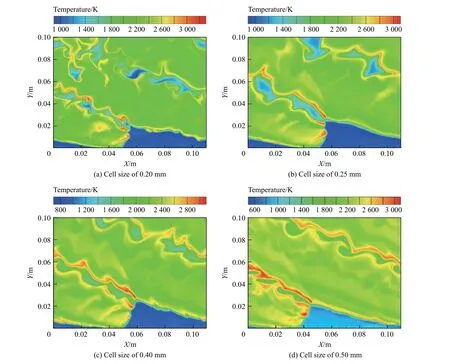
图3 不同网格单元尺寸的温度等值线分布Fig.3 Contours of temperature for different cell sizes

在X=0.02 m，Y=0.01 m 处设置压力监测点，爆轰波传播稳定后，求解监测点处的爆轰波速度：

式中：v为爆轰波平均速度，l为几何模型的X向长度，Ti为爆轰波压力曲线第i个周期，a为所取的周期个数。不同网格尺寸计算所得的爆轰波平均速度、温度和反应区宽度如表3 所示，其中反应区宽度指化学反应速率不为零的区域的宽度。

表3 不同网格尺寸计算所得的爆轰波平均速度、温度和反应区宽度Table 3 Average velocity, temperature and reaction zone of detonation waves calculated for different cell sizes

由表3 可以看出，网格尺寸为0.20 和0.25 mm 时对应的爆轰波参数较接近，结合图3 的流场分布，选取0.25 mm 网格尺寸进行计算。

2 流场分析

2.1 气液两相RDE 流场结构

以初始液滴直径为50 µm 的工况为例，揭示了气液两相旋转爆轰基本流场，如图4 所示。图4(a)显示了典型的旋转爆轰波、斜激波与缓燃接触面三波交汇结构，爆轰波运动方向自左向右，红色区域为煤油液滴分布区域，煤油液滴从爆轰波后注入，在爆轰波单个周期内，波前液滴受高温空气影响蒸发时间最长，因此波前存在无液滴区域（图4(a)中白色框区域）。图4(b)中箭头显示了横波的位置与运动方向。此外，温度场中存在低温条带和爆轰波前液滴与低温反应物三角形区域不重合现象。

在实现企业协同的基础上，要进一步实现高校内部跨校、跨系部、跨专业的人才联合培养。跨越组织机构之间的界限，学校与学校之间、专业与专业之间、科研与教学之间、学科与专业之间形成资源共享，相互支撑相互渗透，为学生提供跨学校、跨专业的教育培养。从而探索建立多学校结合、多学科融合、多团队协同、多技术集成的研发与应用平台，以解决学校批量化人才培养与社会特性化人才需求之间的矛盾。

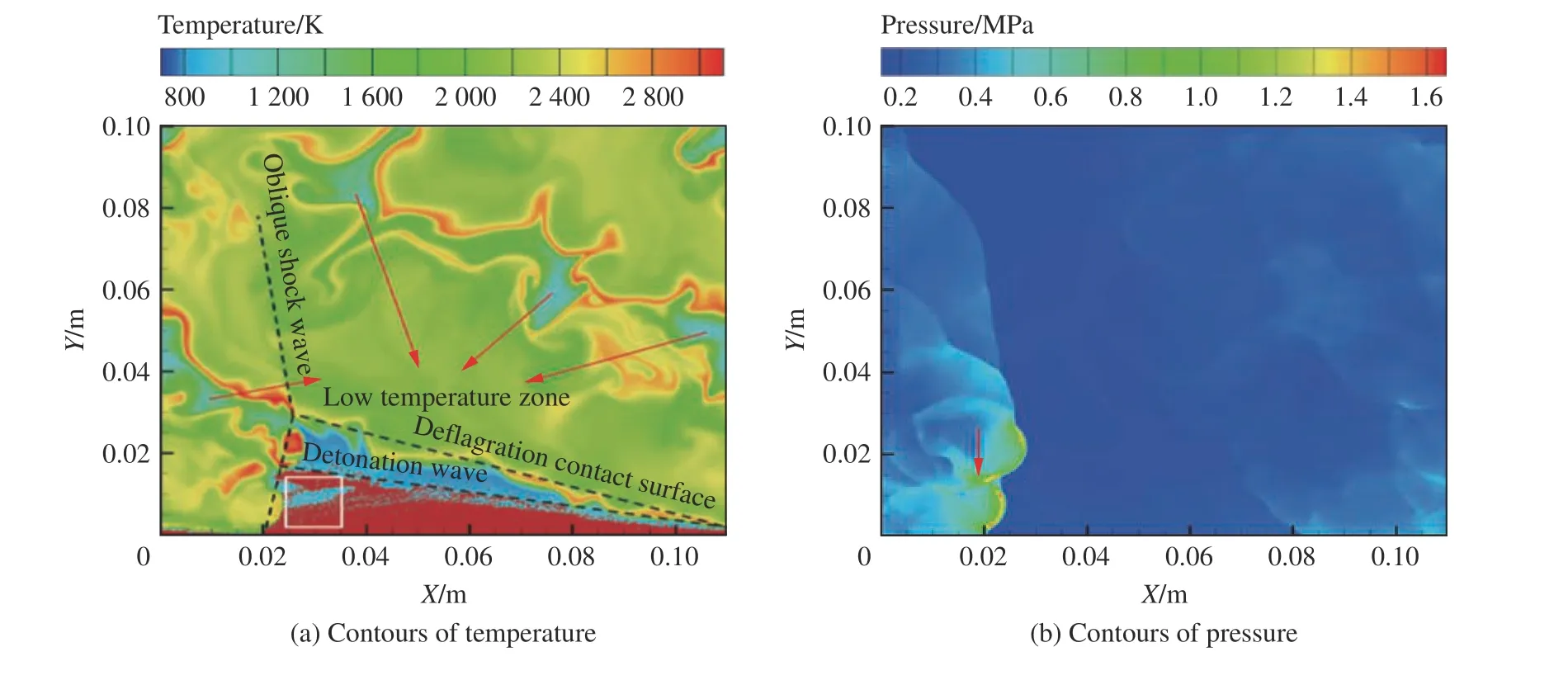
图4 初始液滴直径50 µm 的温度和压力等值线分布Fig.4 Contours of temperature and pressure at an initial droplet diameter of 50 µm

图5 展示了空气Y方向与X方向的速度分布。由图5 可知，RDE 燃烧室X向速度的最大值集中分布在爆轰波处。轴向Y速度最大值在燃烧室出口处可达千米每秒。由于斜激波的运动导致出口流速不均匀。图5(a)给出了局部放大的爆轰波处Y轴方向速度的等值线分布，入口爆轰波后存在一段空气阻塞区，空气Y轴方向的速度达百米每秒，而液滴的初始注入速度为50 m/s，如图6 所示。因此旋转爆轰波后，入射液滴被空气加速，在爆轰波单个旋转周期内，空气的注入高度大于液滴注入高度，导致波前的液滴与空气三角形区域不重合。

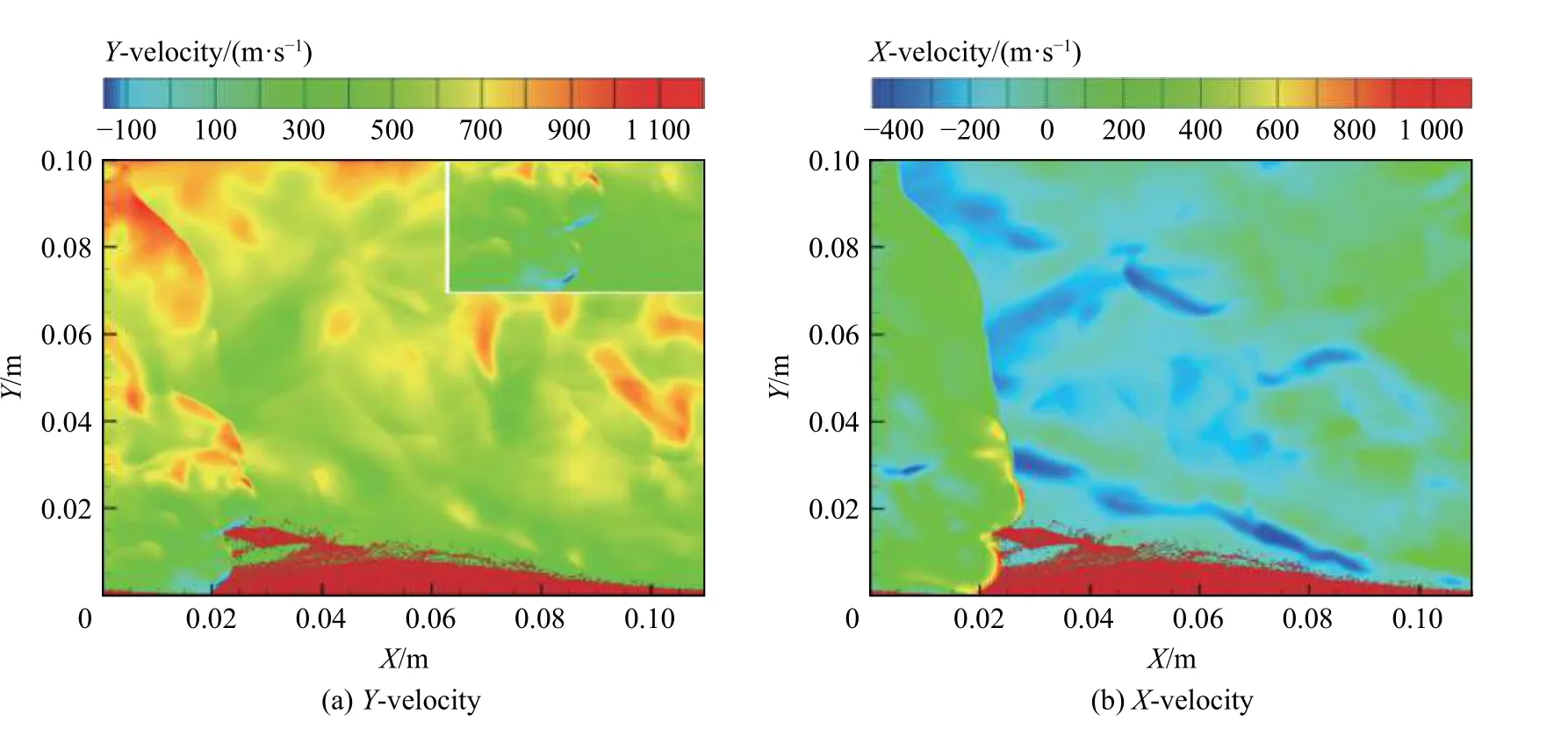
图5 Y 方向速度与X 方向的速度等值线分布Fig.5 Contours of Y-velocity and X-velocity

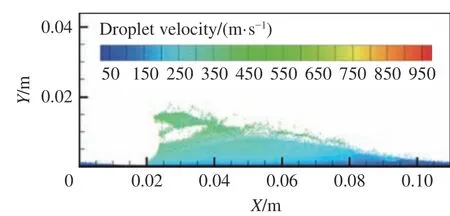
图6 液滴速度等值线分布Fig.6 Contours of droplet velocity

图7 为煤油蒸气质量分数与液滴分布。由图7 可知，爆轰波前煤油蒸气与液滴高度几乎一致。这是由于爆轰波单个旋转周期较短，而煤油液滴蒸发为气相后未来得及扩散（仅箭头所示，微量煤油蒸气向空气层扩散），而爆轰波的传播需要化学反应提供能量，因此爆轰波强度高的范围也主要集中于波前蒸气区域，约20 mm。

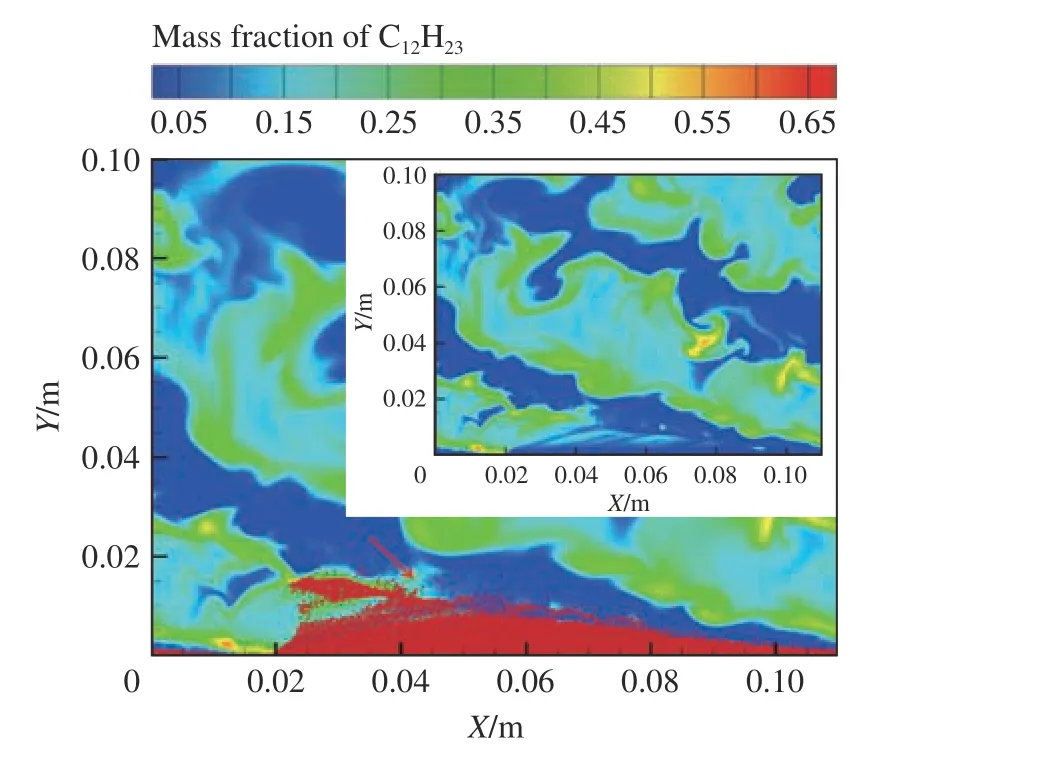
图7 煤油蒸气质量分数和液滴分布Fig.7 Mass fraction of kerosene vapor and distribution of droplets

图8 给出了初始液滴直径为50 µm 的O2、N2和CO2的质量分数等值线分布。由图8 中O2、N2的分布可知，空气三角形最大注入高度约30 mm，且由CO2分布可知波前反应物在高温空气预蒸发过程中未发生提前燃烧。本文中所有工况的燃料三角形区域均无燃料提前反应现象。由图7 推测的爆轰波强度范围低于空气层最大注入高度。因此，爆轰波相对于空气向前运动时，远离燃烧室入口处的空气会分离出去形成低温间断条带，如图4(a)中箭头所示。

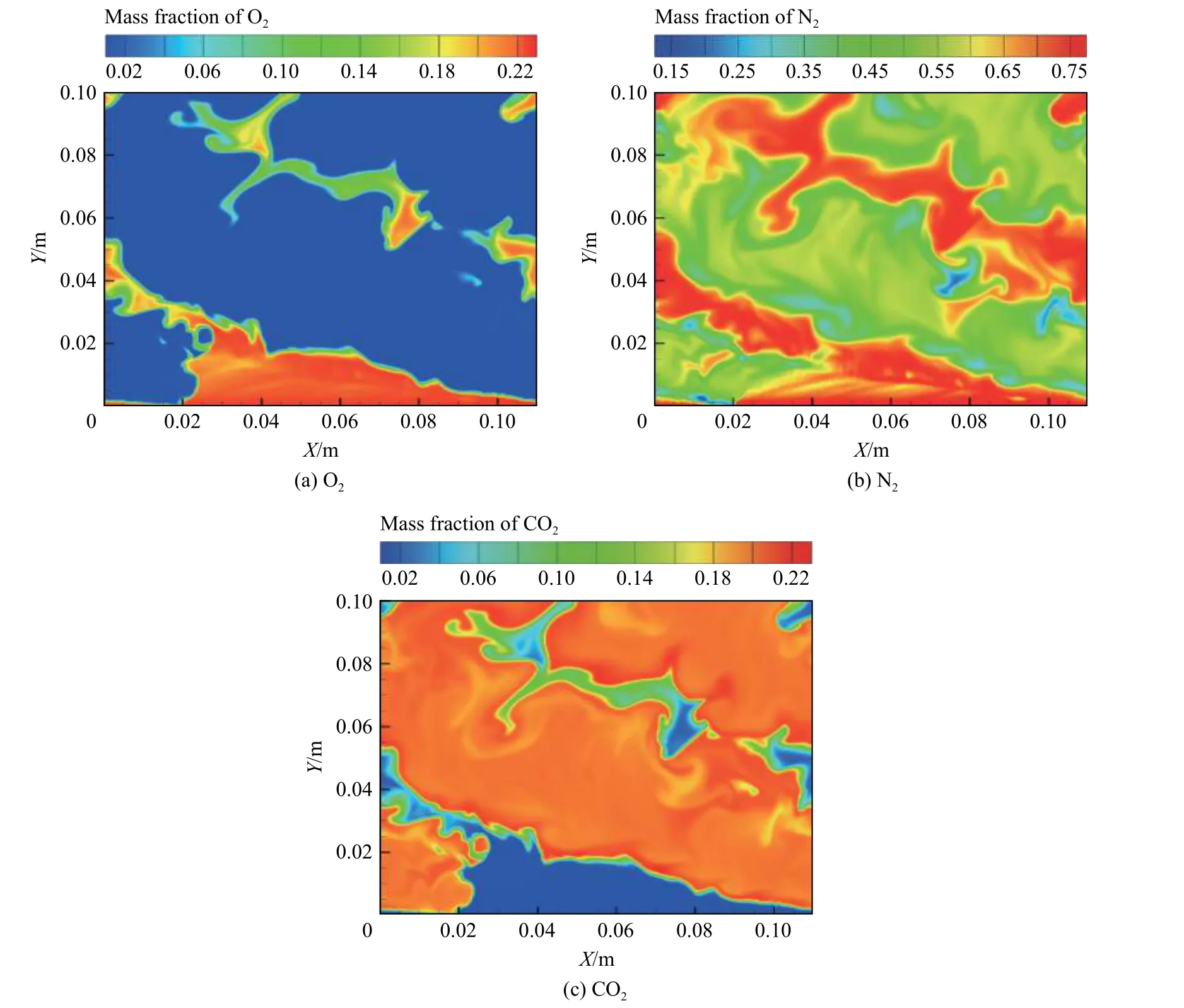
图8 初始液滴直径为50 µm 的O2、N2 和CO2 质量分数等值线分布Fig.8 Contours of mass fractions of O2, N2 and CO2 at an initial droplet diameter of 50 µm

波前的燃料由蒸气和液滴组成，为分析燃料的混合程度，定义当量比[45]：

式中：(mair/mfule)stoic为化学当量的空燃比，mair和mfuel分别为空气和燃料的质量；c为离散相质量浓度；Vcell为网格单元体积；ωC12H23(g)、ωO2、ωN2分别为煤油蒸气、O2和N2的质量分数。爆轰波后存在未燃烧完全的煤油蒸气。由图8 中的O2和N2分布可知，氧化剂几乎被爆轰波消耗，式(23)仅分析波前的混合程度。初始液滴直径为50 µm的爆轰波前当量比等值线分布如图9 所示。本文中，各工况的注入条件保持全局当量比为1，空气区域大于液滴煤油蒸气区域，导致波前燃料空气混合不均匀，波前均存在富油区及贫油区。

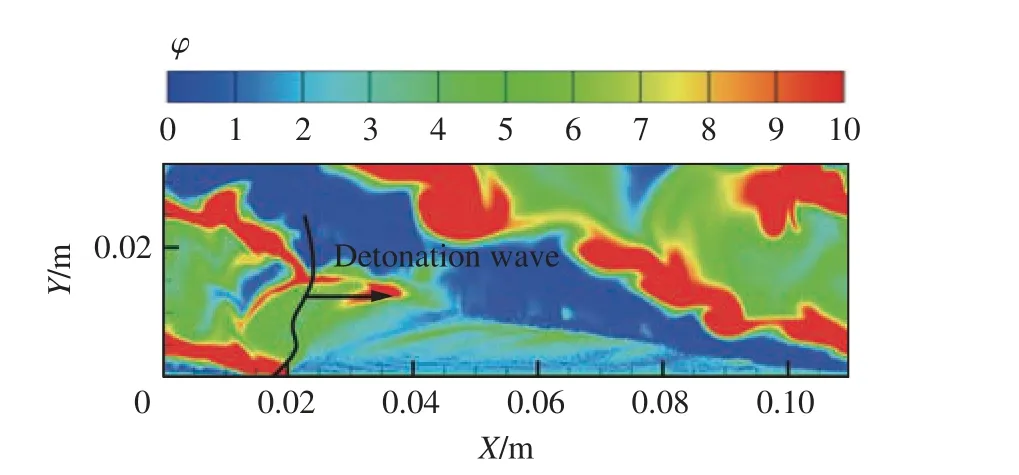
图9 初始液滴直径50 µm 的爆轰波前当量比等值线分布Fig.9 Contours of equivalence ratios before the detonation wave at an initial droplet diameter of 50 µm

2.2 液滴运动分析

2.1 节仅展示了液滴的空间分布。为了更清晰地说明气液两相RDE 燃烧室内液滴的运动规律，绘制了煤油液滴分布示意图，如图10 所示。从图10 可以看出，爆轰波后由高压产生了一段空气阻塞区域，由于离散相采用表面注入方式，爆轰波后液滴仍然可以注入，然后与气相相互作用，红色球表示初始注入的、粒径较大的液滴。爆轰波后区域受膨胀波的影响，压力降低，空气开始注入，且液滴被加速，蓝色箭头所指的注入区域为相对低速空气注入区域。爆轰波阻塞区后部分液滴并未进入产物区域，且与气相相对速度较低，此时液滴不易破碎，缓慢蒸发向下游运动，最终形成较大液滴条带，如图10 中绿色球形液滴所示。红色注入区域为相对高速空气注入区域，此时液滴在与空气较大的剪切作用下发生剧烈破碎，产生较小粒径的紫色球形液滴。流场粒径大小分布如图11 所示。

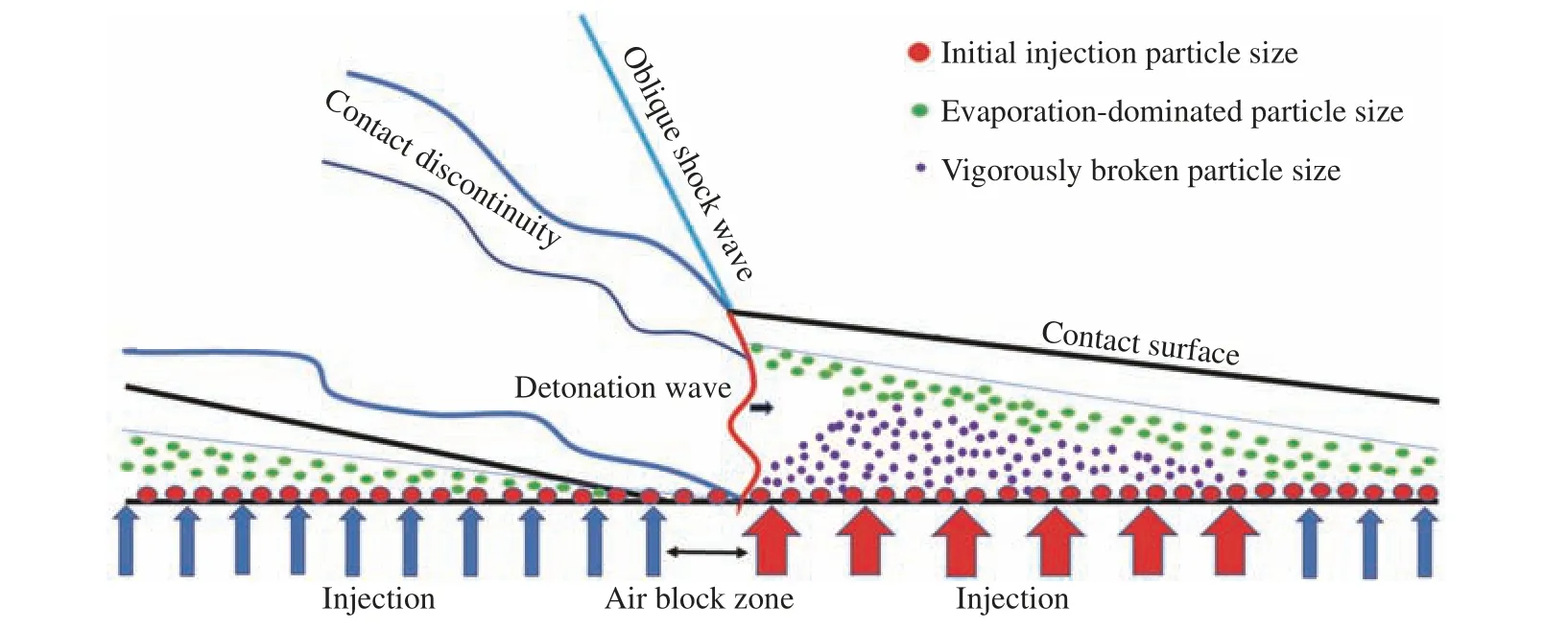
图10 液滴分布示意图Fig.10 Schematic diagram of droplets distribution

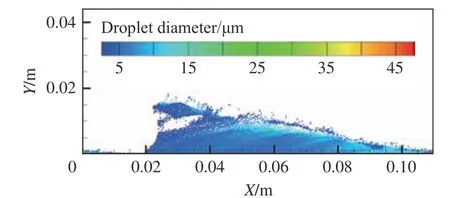
图11 初始液滴直径50 µm 液滴直径等值线分布Fig.11 Contours of the droplet diameter at an initial droplet diameter of 50 µm

在爆轰波传播的单个循环过程中，液滴由爆轰波后注入，爆轰波前远离燃烧室入口的液滴经历的蒸发时间最长，图12 显示了初始液滴直径50 µm 工况下流场中煤油液滴的停留时间等值线分布，最大液滴停留时间为86.9 µs。

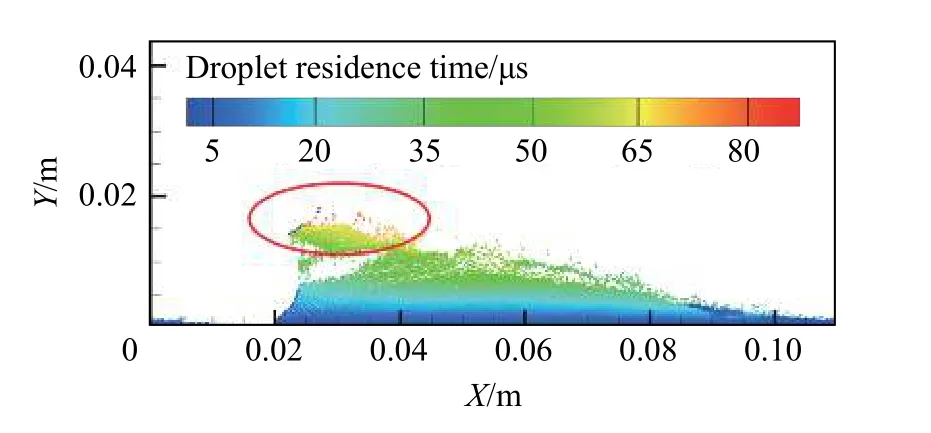
图12 初始液滴直径50 µm 的液滴停留时间等值线分布Fig.12 Contours of the droplet residence time at an initial droplet diameter of 50 µm

2.3 不同初始液滴直径对流场的影响

2.3.1 初始直径1 µm 工况

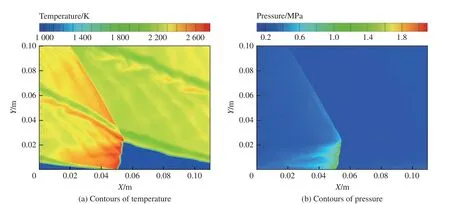
图13 初始液滴直径1 µm 的温度和压力等值线分布Fig.13 Contours of temperature and pressure at an initial droplet diameter of 1 µm

2.3.2 初始直径10～70 µm 工况

图14 为初始直径为10～70 µm 范围工况下旋转爆轰波自持稳定传播后液滴直径等值线分布。

2.2 节中分析了初始直径为50 µm 工况下旋转爆轰流场的液滴直径分布规律，解释了爆轰波前远离入口处较大液滴条带产生的原因。由图14(a)可知，初始液滴直径为10 µm 时，流场中存在大量未破碎的液滴。初始液滴直径增大至20 µm 时，流场中仅混杂少量未破碎的液滴，如图14(b)中的箭头所示。初始液滴直径为30 µm 时，流场中几乎不存在未破碎的液滴。在爆轰波的一个旋转周期内，爆轰波后初始液滴注入，此时主要经历蒸发混合等过程，受空气剪切破碎的影响较小，蒸发速度较慢。

从较小初始液滴直径范围的工况可知，初始液滴直径越小，液滴越具有保持稳定的趋势，越不容易破碎。相应地，对于较大初始液滴直径，如图14(e)和(f)，初始液滴直径越大，液滴越具有不稳定的趋势，在空气作用下越容易发生破碎。这导致随着初始直径的增大，下游的大液滴条带不明显。

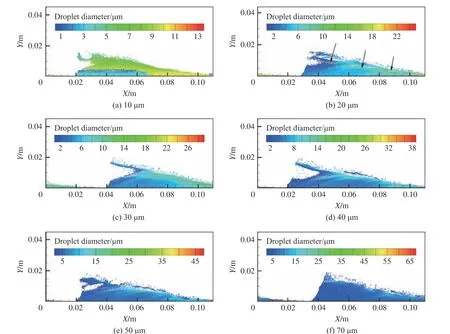
图14 不同初始液滴直径的液滴直径等值线分布Fig.14 Droplet diameter distribution for different initial droplet diameters

定义流场中平均液滴直径[47]：

式中：f(D) 为流场中液滴直径的概率密度分布函数，等式右边分母值为1。

图15 为液滴平均直径随初始液滴直径变化的函数分布。可以看出，除10 µm 工况外，随着初始直径的增大，流场的液滴平均直径先减小后缓慢增大。40～70 µm 的初始液滴直径工况范围内，流场平均液滴直径比10～30 µm 工况更小且差别不大。这再次验证了较大初始直径的液滴更易破碎。可以推断出对于较大的初始液滴直径，不同的初始液滴直径受相同的高速空气流剪切破碎后，总是会破碎成差别不大的液滴直径。

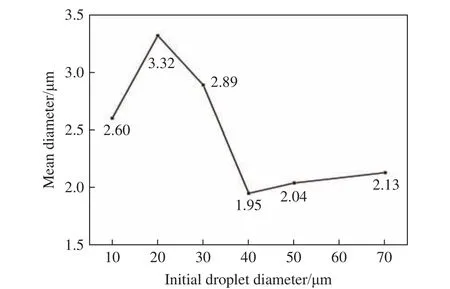
图15 液滴平均直径随初始液滴直径变化的函数分布Fig.15 Droplet mean diameter as a function of the initial droplet diameter

图16 展示了在X=0.02 m、Y=0.01 m 监测点处计算所得的爆轰波平均速度、压力和温度。可以看出，随着初始直径增大，爆轰波的压力波动变化，而爆轰波的温度变化趋势则与爆轰波速度变化趋势基本一致。

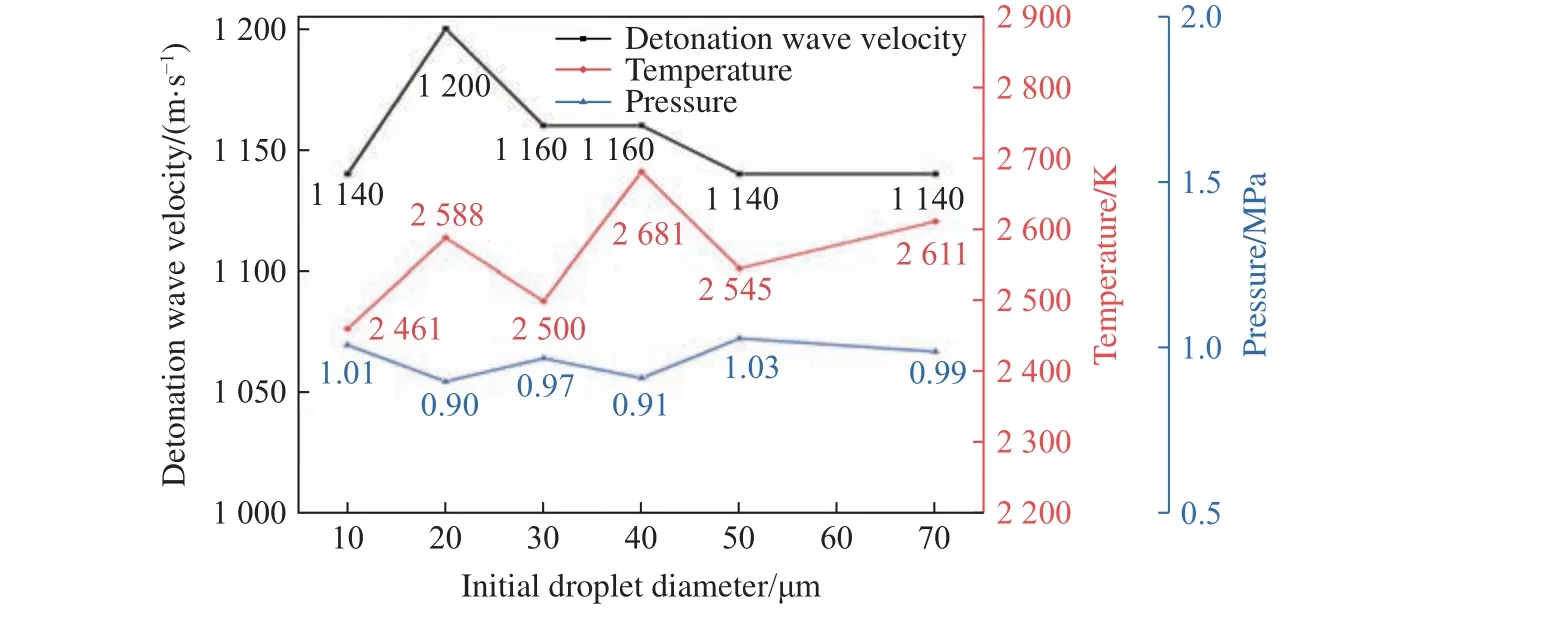
图16 爆轰波速度、温度和压力随初始液滴直径变化的分布函数Fig.16 Detonation wave velocity, temperature and pressure as functions of the initial droplet diameter

表4 给出了不同液滴直径工况流场中液滴最大停留时间和爆轰波周期。在不同工况下，液滴最大停留时间均占爆轰波传播时间尺度的80%以上，保证了爆轰波的自持传播。

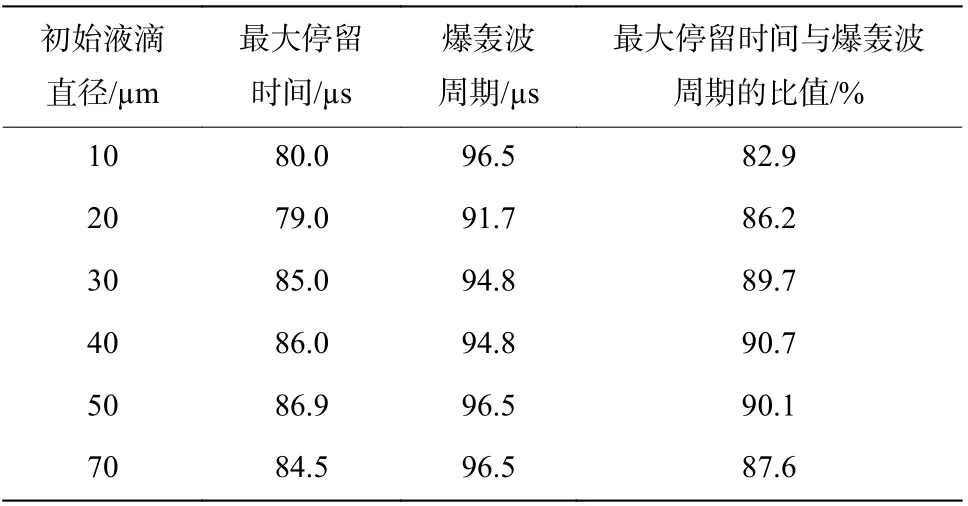
表4 不同初始直径的液滴最大停留时间和爆轰波周期Table 4 Maximum residence time of droplets and detonation cycle time for different droplet diameters

为了分析爆轰波速度发生变化的原因，定义爆轰波波前不同初始直径工况下液滴的蒸发效率：

式(25) 仅计算爆轰波前的蒸发混合过程，爆轰波后无液滴，η 恒为1。

初始直径30 µm 工况的蒸发效率等值线分布如图17 所示。初始直径工况下爆轰波前蒸发效率最高。取工况波前区域求解蒸发效率平均值。工况爆轰波前白色矩形区域划分标准为：Y方向自燃烧室入口沿Y正向延伸，高度为爆轰波高度；X方向宽度均为0.01 m，X坐标自爆轰波的最高点处沿X正向延伸。不同初始直径工况下平均蒸发效率与爆轰波速度的关系如图18 所示。

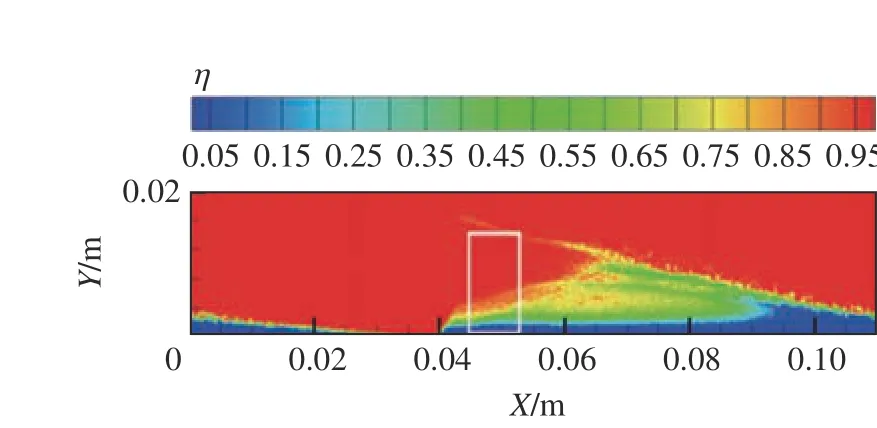
图17 初始液滴直径为30 µm 工况的蒸发效率分布Fig.17 Distribution of evaporation efficiency for an initial droplet diameter of 30 µm

从图18 可以看出，爆轰波波前的蒸发效率与爆轰波速度随初始直径的变化趋势一致。燃料质量流量不变的情况下，改变初始直径，波前蒸发效率较高时，爆轰波前气相燃料与所有燃料的质量比值较大，爆轰波速度较高。

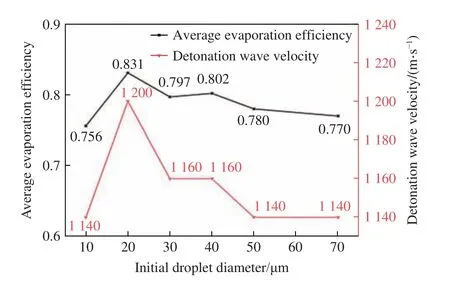
图18 平均蒸发效率、爆轰波速度与初始液滴直径的关系Fig.18 Average evaporation efficiency and detonation wave velocity as functions of the initial droplet diameter

3 结 论

采用单步总包反应机理，考虑液滴的雾化破碎、碰撞黏合过程，采用初始均匀直径假设，在直径1～70 µm 工况范围内计算了二维RDE 的气液两相流流场，得出以下主要结论。

(1) 不同初始液滴直径工况下，旋转爆轰燃烧室内均形成了稳定传播的爆轰波，由于波前液滴与煤油蒸气分布不均匀，爆轰波呈现曲面分布。仅当初始直径减小至1 µm 时，爆轰波才变得更平整，呈现出气相爆轰特性。

(2) 初始液滴越小，越具有保持稳定的趋势，在爆轰波周期内受高温空气作用，此时主要经历蒸发过程。而初始液滴越大，越易破碎成小液滴，此时受空气破碎影响较大。

(3) 对于相同的燃料质量流量，在不同初始液滴直径工况下，爆轰波前燃料的蒸发效率越高，爆轰波速度越大。初始直径为10～70 µm 工况下，随着初始液滴直径的增大，爆轰波速度先升高后降低，爆轰波速度极大值出现在初始液滴直径为20 µm 的工况。