冲击荷载作用下滤波混凝土的动态响应与层裂损伤数值研究*
李国强,马 钢,高松涛,郭栋才,张佳寅
(太原理工大学土木工程学院,山西 太原 030024)
爆炸冲击波是一种瞬间强压缩波,会对结构和人员造成重大伤害。目前,国防工程和民用工程防护结构使用最广泛的是厚度达数米的钢筋混凝土结构。在现代高技术战争条件下,相比于造价动辄千万的巨型动能钻地弹,成本较低且精度日益提升的高爆弹对国防和民用基础防护工程的威胁更显著,其产生的爆炸冲击波会在混凝土内部形成峰值较高、持续时间较短的压缩应力波[1-2]。压缩波在传播至防护结构背部自由面时会发生反射并转换为拉伸波,并与压缩波的卸载段发生耦合作用,导致靠近防护结构背部自由面某处形成较高的拉应力[3]。由于混凝土具有脆性和较低的抗拉强度,结构背部的混凝土极易发生严重的层裂破坏,甚至造成崩落,产生的混凝土碎块将会对附近的人员和设备构成巨大威胁。而混凝土的层裂崩落可在防护结构中形成新自由表面,应力波在自由面的多次反射将加剧混凝土防护结构背部的层裂破坏。因此,研究混凝土结构在爆炸冲击强动荷载下的动态响应与层裂破坏具有重要的工程意义。
近年来,学者们对强动荷载作用下混凝土材料中的应力波传播规律及层裂损伤进行了大量的研究。郭弦等[4]通过霍普金森杆实验研究了混凝土试件中应力波的传播规律,发现当应力波峰值在混凝土中衰减到某一特定值后便不再衰减,并保持该特定值继续传播。巫绪涛等[5]通过数值模拟研究了应力波在混凝土中传播的衰减规律,发现应力波在混凝土中的衰减与试样的初始脉冲强度密切相关,当霍普金森压杆(split Hopkinson pressure bar, SHPB)实验所采用的细长试件的长径比大于15,或传入试样的初始脉冲强度低于混凝土抗压强度时,应力波的衰减可忽略不计。俞鑫炉等[6]对混凝土一维应力层裂实验进行了全场DIC 分析,发现混凝土试件各位置的裂纹均由透射压缩波与反射拉伸波叠加而成。综上可知,混凝土结构在强动荷载下易产生层裂损伤的根本原因,除了混凝土材料存在显著的拉压不对称性外,弹性应力波在混凝土中的传播几乎无沿程衰减也是问题的关键[4-5]。提高混凝土材料的强度或加大结构厚度属于被动抵御,只有通过技术手段增大应力波在混凝土结构中的沿程衰减,并降低应力波的峰值强度,从而抑制反射拉伸波,使混凝土结构对强动荷载做出主动响应,才能从根本上降低混凝土结构背部的层裂破坏程度。
Liu 等[7-8]通过将涂有硅橡胶的铅球嵌入环氧树脂基体中,制作出了局域共振声子晶体,该类结构对弹性波产生了明显的衰减作用。基于此,研究人员将包裹有软涂层的金属芯填充到砂浆或混凝土基体中,设计出了局域共振混凝土,并对该类混凝土进行了大量研究。Mitchell 等[9-10]通过数值模拟方法研究了局域共振混凝土在爆炸荷载下的响应情况,发现在带隙范围内应力波峰值出现明显衰减。张恩等[11]利用数值模拟方法研究了局域共振混凝土的带隙特征,发现局域共振混凝土对冲击波具有更好的衰减作用。Jin 等[12]通过解析推导和数值模拟方法研究了爆炸荷载作用下局域共振混凝土的动态响应,发现局域共振混凝土中的人工单元能够有效存储应力波中的能量,从而降低砂浆基体中的能量。Xu 等[13]通过将包有软涂层的钢球作为人工骨料随机分布在砂浆基体中,制作出了局域共振混凝土试件,并进行了冲击力学实验,发现人工骨料的加入使局域共振混凝土对带隙范围内的应力波产生了衰减效果。
基于局域共振结构的带隙特性,本文中,将由弹性层和金属球组成的滤波单元均匀嵌入混凝土基体中,设计出具有应力波衰减效应的滤波混凝土。通过将滤波混凝土模型简化为质量弹簧力学系统来研究滤波混凝土对应力波的衰减机制。利用LS-DYNA 软件建立滤波混凝土有限元模型,通过数值模拟方法,对比冲击荷载作用下普通混凝土模型和滤波混凝土模型中的应力波沿程传播特性和层裂破坏模式。通过参数分析研究铅球密度、弹性层刚度和厚度等因素对滤波单元储能效果的影响。
1 应力波衰减机制
通过负有效质量效应来描述滤波混凝土衰减应力波的工作机制[14-15]。在滤波混凝土结构中,取图1 所示的基本单元为研究对象。滤波混凝土基本单元由金属球、弹性层和圆柱状混凝土基体组成。将基本单元简化为图2 所示的质量弹簧力学系统,其中m1和µ1分别为外部混凝土基体的质量和位移,m2和µ2分别为内部金属球的质量和位移,弹性层可简化成刚度系数为k2的线性弹簧用于金属球与混凝土基体的连接。假设弹性层为均匀弹性材料,并在简化过程中忽略弹性层的质量。
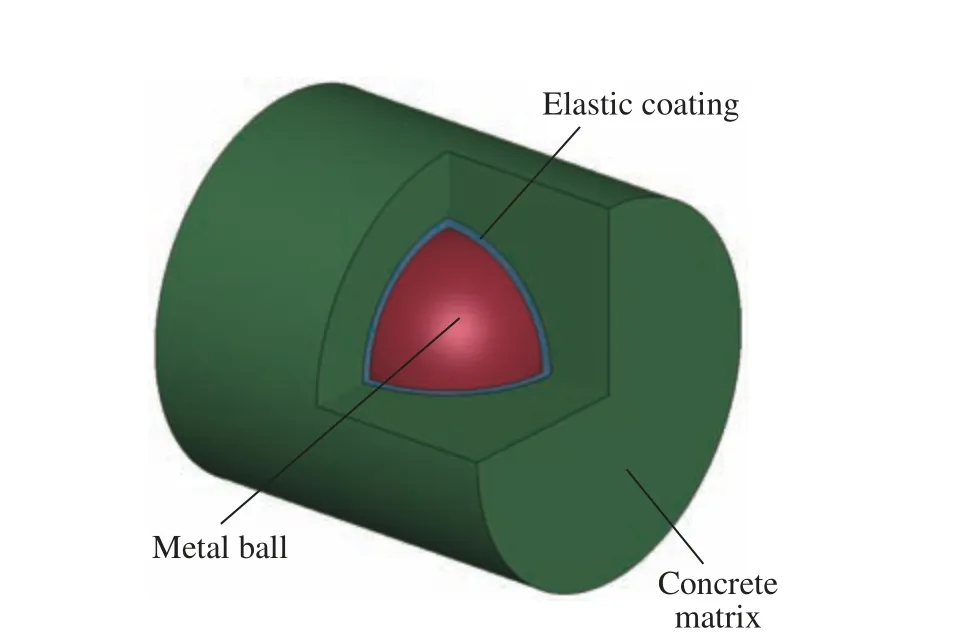
图1 滤波混凝土基本单元Fig.1 Basic unit of filter concrete
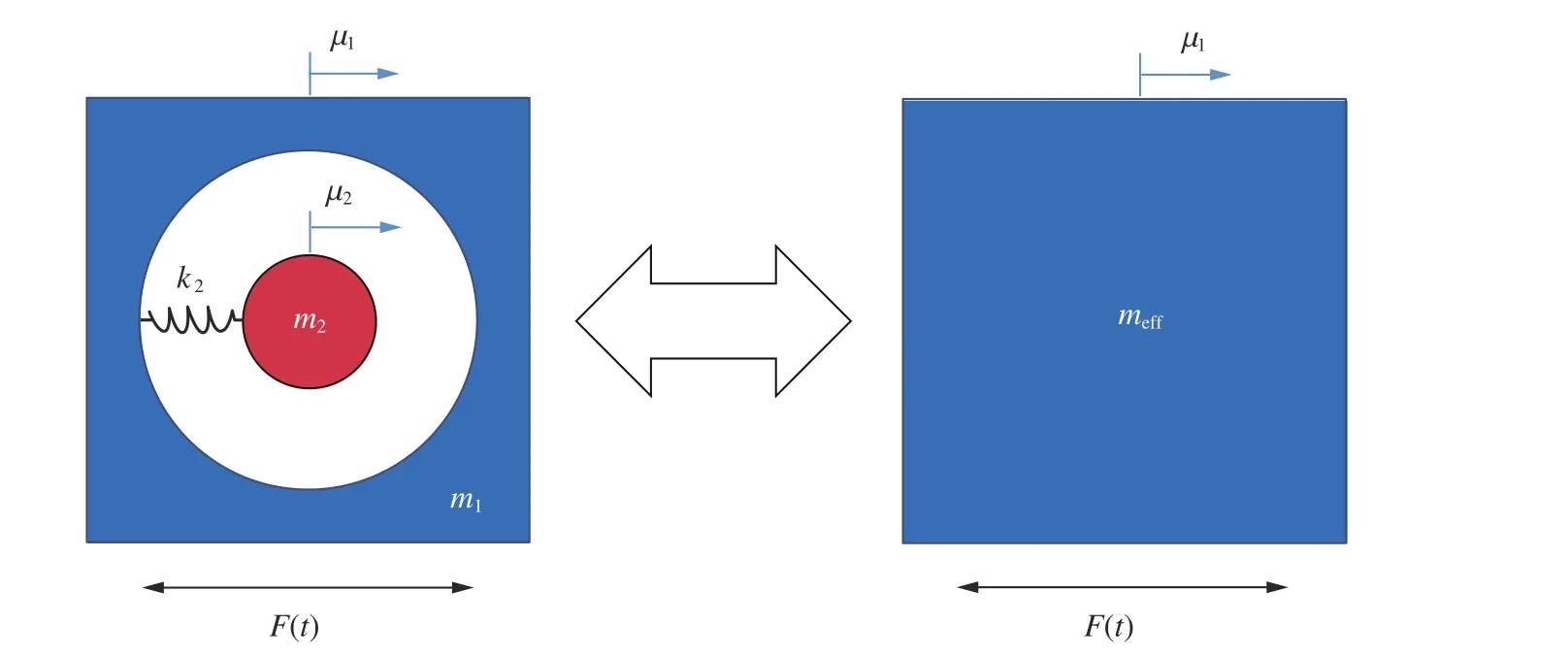
图2 质量弹簧力学系统Fig.2 Mass-spring mechanical system
根据动力学平衡方程,在外荷载F的作用下,可得到:
假设该力学模型的运动遵循稳态的简谐振动,则有:
通过求解上述方程,可得到:
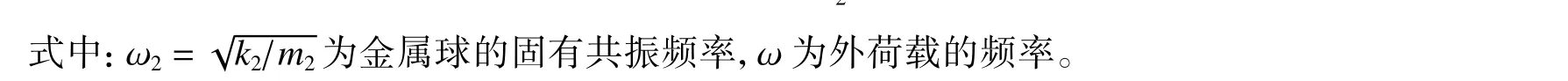
如果用单一质量体meff来等效代替基本单元中m1和m2,并产生相同的运动行为,需满足:
联合式(5)~(6)进行求解,可得到:
式 中:θ =m2/m1,mst=m1+m2。
根据式(7),当θ=1 时,meff/mst与ω/ω2的关系如图3 所示。当ω/ω2处于图3 中M与N两点之间的区域时,有效质量达到负值,并且在M点附近负有效质量效应将出现放大。如果质量为负,根据牛顿第二定律,金属球的加速度将与所施加的荷载方向相反,使得基体材料的运动受到抑制,并产生局域共振带隙[16-17]。应力波在该频率范围内会发生衰减,甚至完全被阻断。滤波混凝土内部形成的局域共振带隙使得它具有独特的滤波特性,从而能够对应力波产生很好的衰减作用。
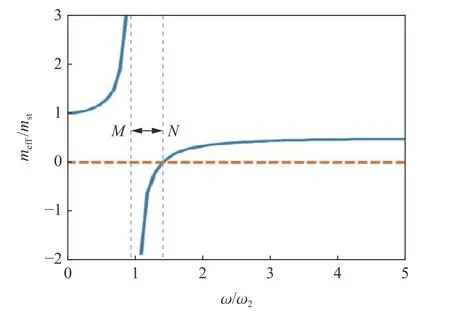
图3 meff/mst 与ω/ω2 的函数关系Fig.3 Function relationship between meff/mst and ω/ω2
2 冲击荷载作用下滤波混凝土应力波衰减数值分析
2.1 滤波混凝土三维数值模型
2.1.1 材料与几何模型
采用LS-DYNA 中的Concrete Damage Re l3 (MAT_72R3)塑性损伤模型对混凝土材料进行模拟。该材料模型考虑了材料塑性、剪切损伤和应变率效应,可以有效模拟混凝土材料在高应变率、大变形下的力学形态。在该混凝土材料模型中,应力张量由静水应力张量和偏应力张量组合表示。静水应力张量改变混凝土体积,偏应力张量控制变形的形状。对于静水应力张量,压实模型在内能上是线性的。压力定义为:
式中:E0为初始体积内能;γ 为比热比;εV为体积应变,由相对体积V的自然对数给出。如图4(a)所示,当体积应变超过弹性极限点时,混凝土发生压实行为。在压实状态下,体积卸载模量与最大体积应变有关,卸载过程沿卸载体积模量至张力截止点进行,重新加载始终遵循卸载路径至开始卸载的位置,并在加载路径上继续加载。
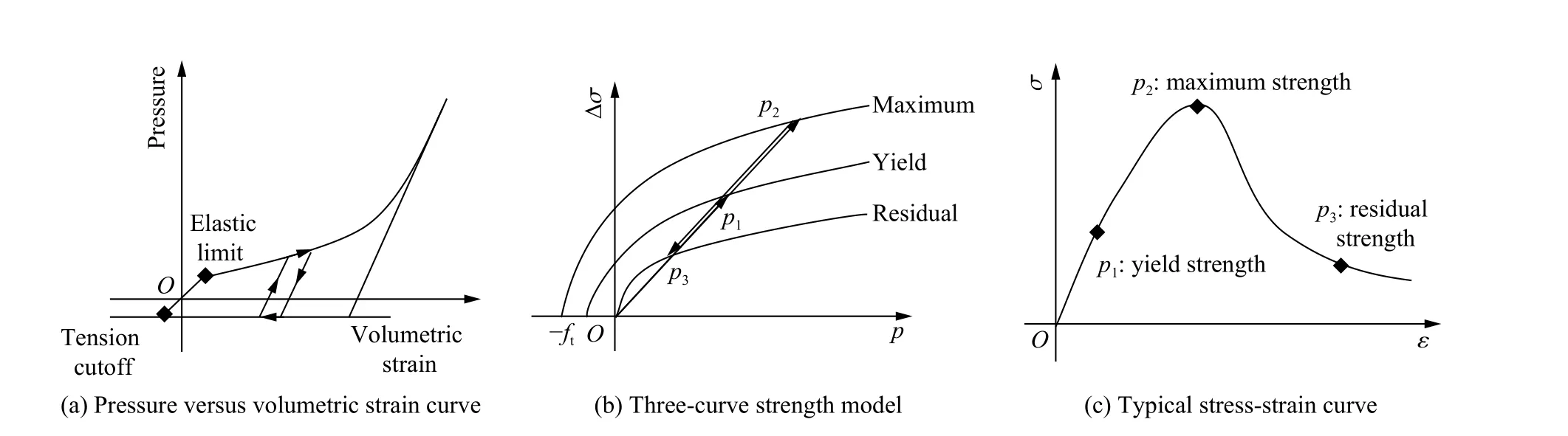
图4 混凝土材料本构模型Fig.4 Constitutive model of concrete material
偏应力采用如4(b)所示的三曲线强度模型,即初始屈服强度曲线、极限强度曲线和残余强度曲线,分别描述混凝土的初始屈服强度、极限强度和残余强度的变化规律。
初始屈服强度曲线为:

对于滤波单元,选取天然橡胶为弹性层材料,铅为金属球材料。采用Mat_Elastic 模拟弹性层与金属球。在模拟中,假设弹性层与金属球均为线弹性材料。表1~2 给出了以上3 种材料的材料参数。表中:ρ 为密度,σc为抗压强度,σt为抗拉强度,E为弹性模量,µ为泊松比。

表1 混凝土的材料参数Table 1 Material parameters of concrete
通过LS-DYNA 建立如图5 所示的滤波混凝土有限元模型,以此来研究冲击荷载下滤波混凝土中应力波衰减的动态行为。该滤波混凝土模型由金属球、弹性层和混凝土基体3 部分组成,6 个被弹性层均匀包裹的金属球等间距同轴排列于混凝土基体中。冲击荷载沿着模型纵向均匀施加于表面上,模型四周为自由边界条件,如图6 所示。其中L为模型的长度,D为模型的横截面的直径,l为相邻2 个金属球中心之间的距离,r为金属球半径,T为弹性层厚度。该模型的几何参数取值由表3 给出。

表3 滤波混凝土模型的几何参数Table 3 Geometric parameters of the filter concrete model

图5 滤波混凝土有限元模型Fig.5 Finite element model of filter concrete
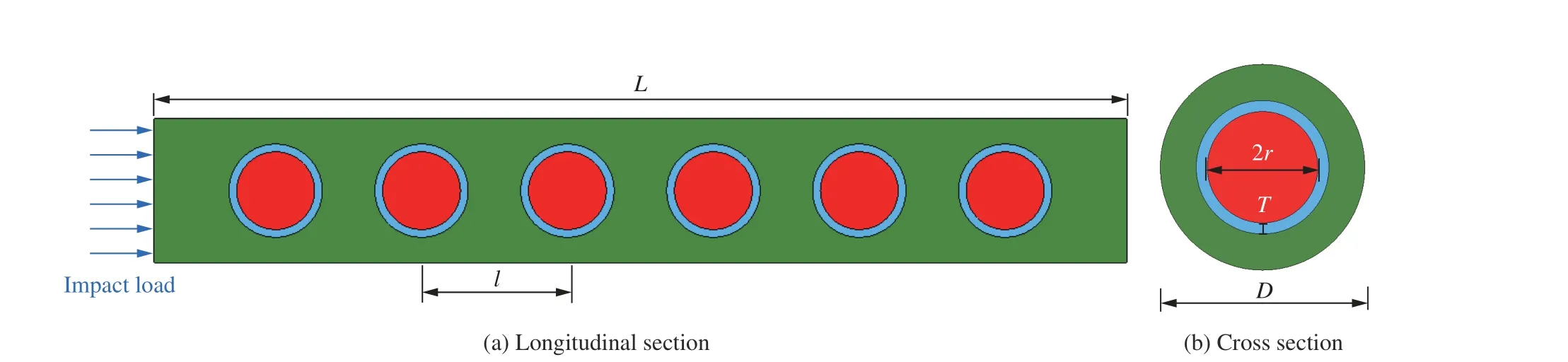
图6 滤波混凝土模型截面示意图Fig.6 Sectional diagrams of filter concrete model
2.1.2 应变率效应
混凝土材料的力学性能与应变率密切相关。随着应变率的提高,材料的抗压与抗拉强度会有不同程度的提高。在模拟中通过考虑应变率-动态强度增强系数来实现混凝土材料的应变率效应。
混凝土的压缩动态强度增强系数 φc[18]为:
混凝土的拉伸动态强度增强系数 φt[19]为:
式中:l g γs=6.156α-2 ,α =1/(5+9fcs/fc0) ,fc0=10 MPa,fcs为静态抗压强度;l gβ=6δ-2 ,δ =1/(1+8fcs/fc0) ;ε˙s=10-6s-1为静态应变率。
2.1.3 单元侵蚀准则
在模拟中,金属球、弹性层和混凝土基体的单元类型均为单点积分的六面体拉格朗日实体单元,各单元之间为共节点连接以传递力和位移。为了模拟混凝土材料在荷载作用下的剪切、破碎和层裂等破坏效果,通常采用侵蚀算法(Add_Erosion)[12,20]。在对不同侵蚀准则进行了大量模拟研究后,最终以0.01 的最大主应变作为混凝土材料的侵蚀准则。
2.2 模型有效性验证
本文中,滤波混凝土模型尺寸设计基于Wu 等[21]的混凝土试件。为验证数值模型的有效性,将该滤波混凝土模型替换为Wu 等[21]实验研究中的同尺寸普通混凝土模型。对该模型施加如图7 所示的实验冲击荷载,并与实验结果进行对比。图8 展示了距离荷载施加面150 mm 处混凝土的应变时程曲线,图9展示了混凝土模型与混凝土试件在冲击荷载下的破坏形态对比。从图8~9 可以看出,普通混凝土模型的应变时程曲线和破坏模式与Wu 等[21]的实验结果基本吻合,验证了本文中数值模型的有效性。
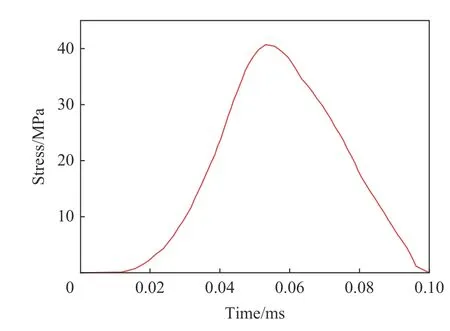
图7 实验[21]中的冲击荷载曲线Fig.7 Impact loading curve in the experiment[21]
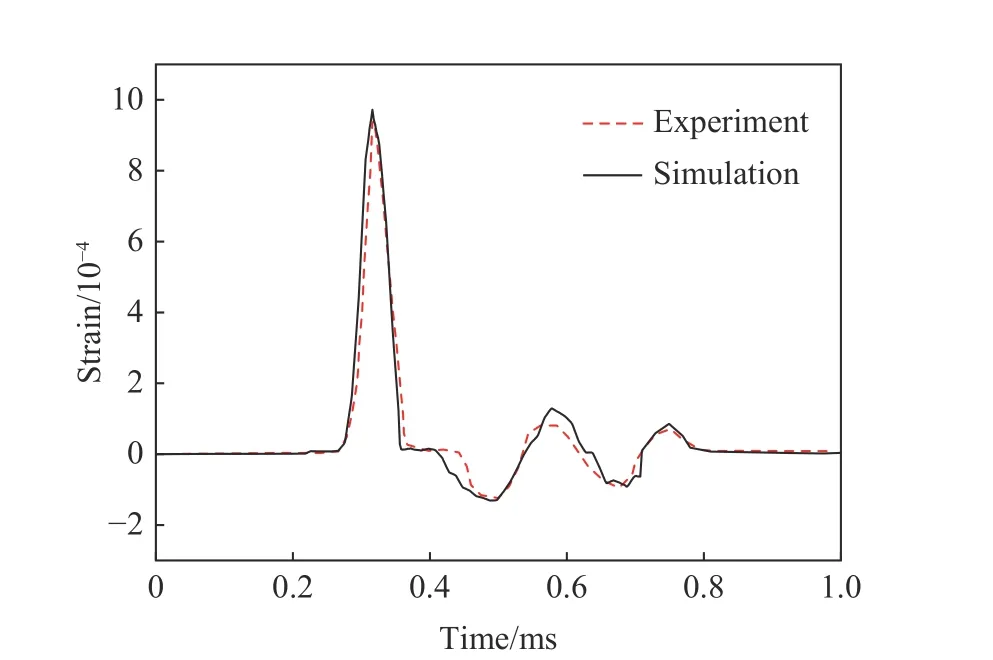
图8 数值模拟与实验条件下混凝土的应变时程曲线Fig.8 Strain time history curves of concrete under numerical simulation and experiment

图9 实验与数值模拟条件下的破坏形态对比Fig.9 Comparison of failure patterns under experiment and numerical simulation
2.3 滤波混凝土对应力波的衰减效应
冲击荷载施加在模型一端后,在模型中会产生沿纵向传播的一维应力波。为了重点研究滤波混凝土及普通混凝土模型中应力波沿程变化规律,对滤波混凝土模型及普通混凝土模型施加如图10 所示的峰值为10 MPa 的冲击荷载,以确保各部分均处于弹性响应范围而不发生材料损伤。在模型中选取S1~S5 的5 个横截面并记录冲击荷载作用下各截面的平均应力,通过对比滤波混凝土模型和普通混凝土模型中应力波的传播特性来检验滤波混凝土对应力波的衰减效果。同时选取截面S0 上铅单元E1 和基体单元E2 并记录各单元的位移变化来反映滤波混凝土模型中不同部分的位移响应情况。截面S0~S5 分别位于距离荷载施加面62.5、25.0、100.0、250.0、400.0和475.0 mm 处。各截面与单元的选取位置如图11 所示。
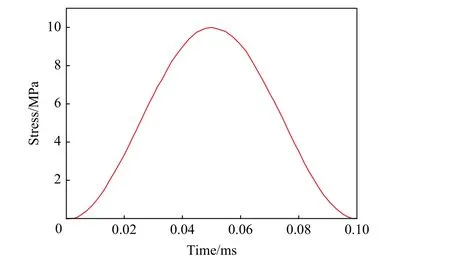
图10 峰值为10 MPa 的冲击荷载曲线Fig.10 Impact load curve with the peak value of 10 MPa
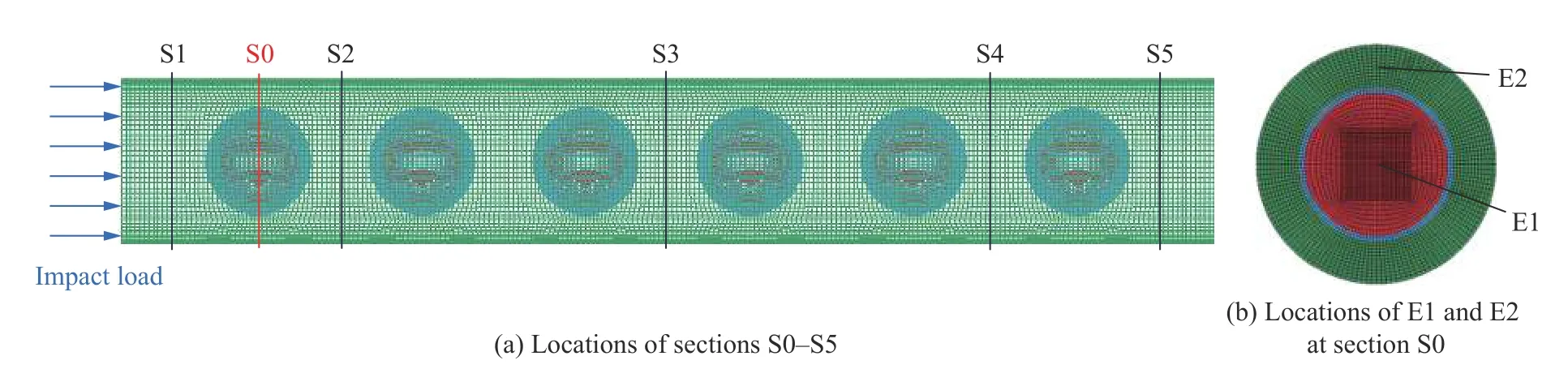
图11 截面与单元选取位置示意图Fig.11 Location diagrams of sections and elements selected
当冲击荷载作用于模型时,会在模型的荷载施加面产生压缩应力波。图12 展示了普通混凝土模型和滤波混凝土模型中截面S1~S5 的平均应力时程曲线。从图12(a)中截面S1~S4 的第一压缩应力峰值可知,压缩应力波在普通混凝土模型中传播时并未发生衰减,这是由于入射压缩波的峰值应力强度低于混凝土抗压强度。低于抗压强度的弹性压缩波仅产生由于几何弥散导致的线性衰减,衰减幅度极小[5]。每个截面的相邻应力峰值对应的间隔时间均相同,说明应力波在普通混凝土模型中传播速度不会衰减。通过图12(b)中截面S1~S4 的第一压缩应力峰值可以看出,当压缩波在滤波混凝土模型中传播时,截面S1~S4 的第一压缩应力峰值随时间出现明显的降低,这说明应力波在滤波混凝土模型中进行沿程衰减传播。图13 为普通混凝土模型和滤波混凝土模型在0.140 ms 时的纵截面应力云图,此时压缩应力波尚未到达模型自由面。从图13 可以看出,滤波单元的存在使滤波混凝土基体中的应力波产生了衰减。对比图12(a)和(b)可以看出,滤波混凝土模型中截面S2 处的第一压缩应力峰值为8.57 MPa(t=0.088 ms),截面S4 处的第一压缩应力峰值为6.02 MPa(t=0.180 ms),相比于普通混凝土模型中截面S2 处的第一应力峰值10.00 MPa(t=0.080 ms)和截面S4 处的第一应力峰值99.94 MPa(t=0.170 ms),分别降低了14.3%和40.0%。滤波混凝土模型中应力波第一次到达S2~S5 各截面的时间相比于普通混凝土模型中的时间均发生了延长,这说明应力波在滤波混凝土模型中的传播速度也发生了衰减。
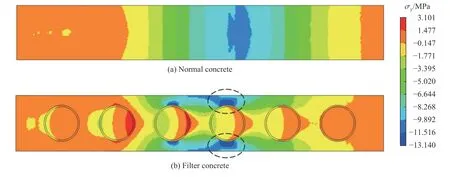
图13 模型在0.140 ms 时的纵截面应力云图Fig.13 Stress contours of the model in the longitudinal section at 0.140 ms
根据应力波在固体结构中的传播规律,当入射压缩波传播到模型的自由面时,压缩应力波会发生反射并转换为拉伸应力波。从图12(a)中截面S2~S4 的第一拉伸应力峰值可以看出,反射拉伸波在普通混凝土模型中传播时出现了衰减,这是由于拉伸波的峰值应力强度超出了混凝土抗拉强度。高于混凝土抗拉强度的塑性拉伸波会在传播过程中发生快速衰减[5],但应力波在混凝土中的衰减并不是自始至终的,当应力波的峰值应力衰减到某一特定值后将会保持该值进行无衰减传播。从图12 可以看出,截面S5的应力峰值较低,这是由于该截面比较靠近模型的自由面,自由面附近发生的应力波转换和应力叠加现象降低了截面S5 的平均应力峰值。图14 为压缩应力波在模型自由面发生反射后普通混凝土模型和滤波混凝土模型在0.270 ms 时的纵截面应力云图。从图14 可以看出,滤波混凝土模型中的拉伸应力明显低于普通混凝土模型中的拉伸应力。对比图12(a)和(b)可以看出,滤波混凝土模型在截面S4 处的第一拉伸应力峰值为6.25 MPa(t=0.240 ms),相比普通混凝土模型在同一截面处的第一拉伸应力峰值9.01 MPa(t=0.228 ms),降低了31.3%。
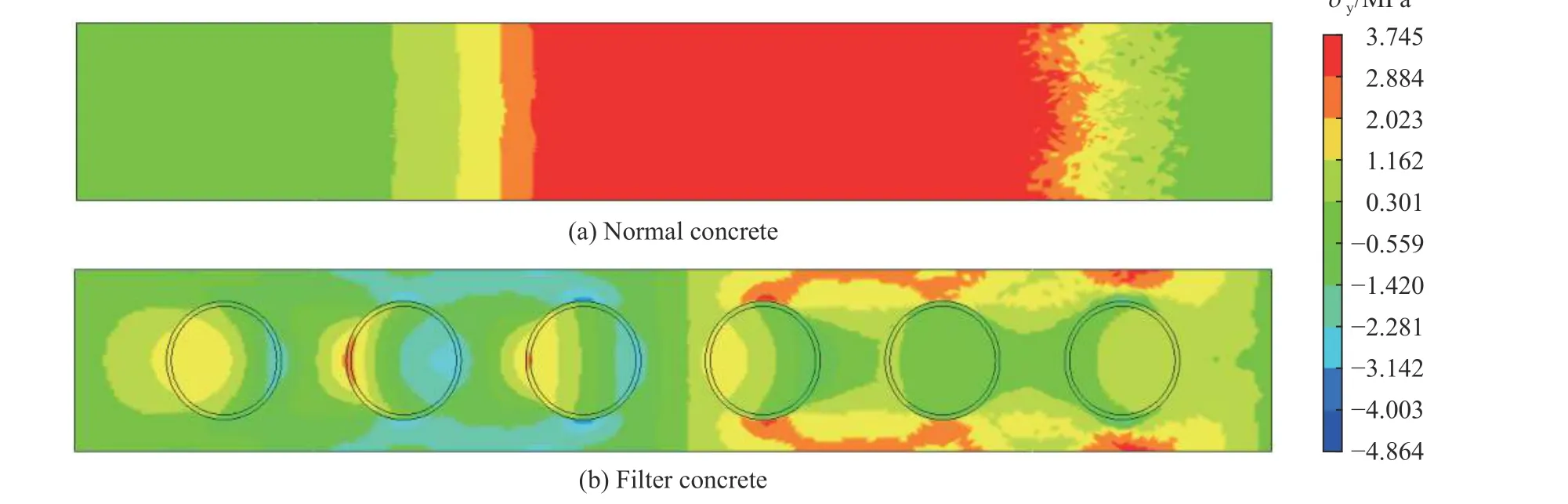
图14 模型在0.270 ms 时的纵截面应力云图Fig.14 Stress contours of the model in the longitudinal section at 0.270 ms
图15 展示了普通混凝土模型和滤波混凝土模型中单元E1 与E2 的位移时程曲线。从图15 可以看出,在普通混凝土模型中,这2 个单元的位移响应情况基本一致;在滤波混凝土模型中,这2 个单元的位移响应呈现出周期性交替的状态,并且在运动开始时铅单元的响应时间滞后于混凝土单元。这说明在冲击荷载下滤波混凝土中的铅球由于弹性包覆层的存在而与混凝土基体做相对往复运动,并对混凝土基体的动态行为产生抑制效果。
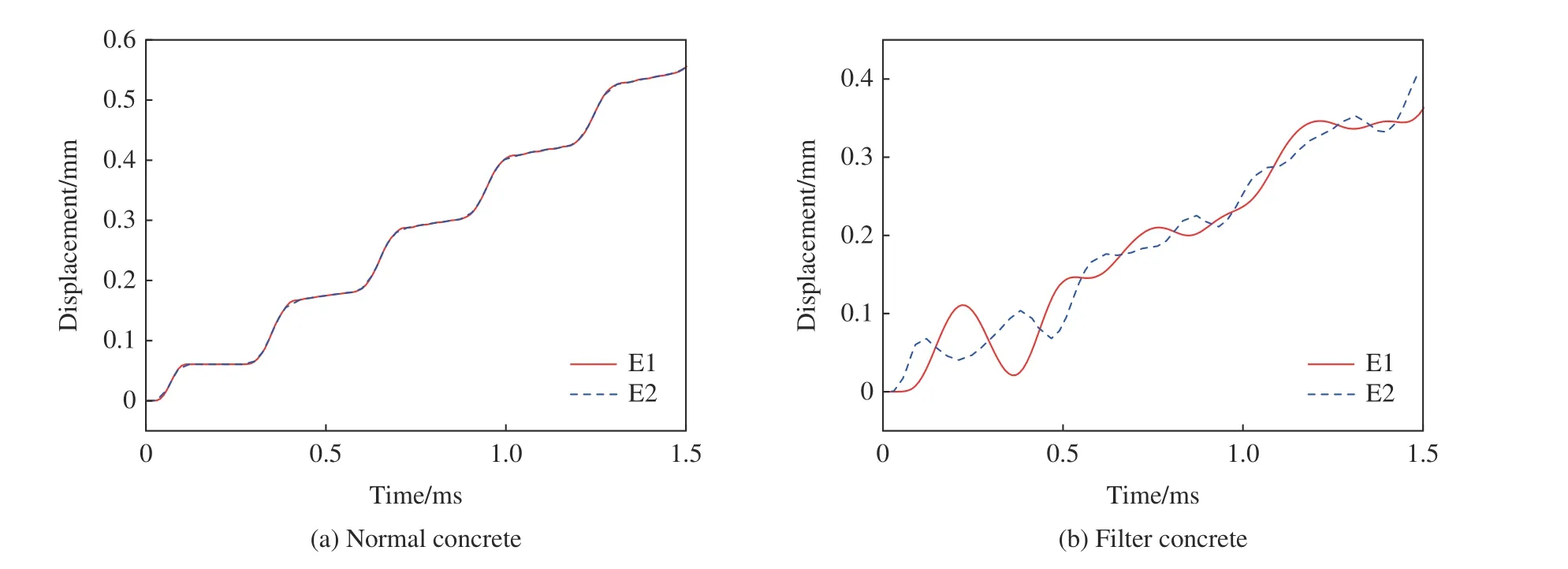
图15 单元E1 与E2 的位移时程曲线Fig.15 Displacement time history curves of elements E1 and E2
图16 展示了滤波混凝土模型中各部分的能量时程曲线,图中所示的能量为各部分动能与势能之和。从图16 可以看出,金属球与弹性层所存储的能量具有波动性,并随着金属球的振动而发生转化。当金属球与弹性层的能量之和达到最大值时,混凝土基体所存储的能量降到最低。滤波单元的储能效应使得混凝土基体对冲击波具有了一定的衰减能力。
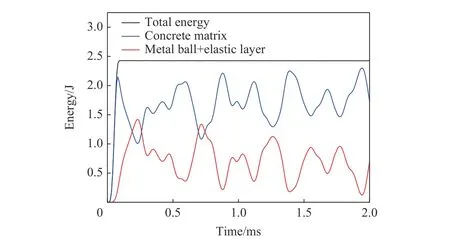
图16 滤波混凝土模型中各部分的能量时程曲线Fig.16 Energy time history curve of each part in the filter concrete model
以上结果表明,由包裹弹性层的金属球组成的滤波单元可以有效地降低冲击荷载作用下滤波混凝土中的应力波沿程传播速度和应力峰值。但是由于较软弹性层的存在,滤波混凝土基体中存在应力集中现象,如图13(b)中的虚线区域所示。图17 展示了滤波混凝土模型截面S0 处弹性层附近混凝土基体单元E3~E5 的应力时程曲线,可以看出,距离弹性层最近的基体单元E3 的峰值应力远大于E4 和E5 单元的峰值应力,说明弹性层周围的混凝土基体中存在明显的应力集中现象,导致弹性层周围的混凝土基体更容易发生损伤。
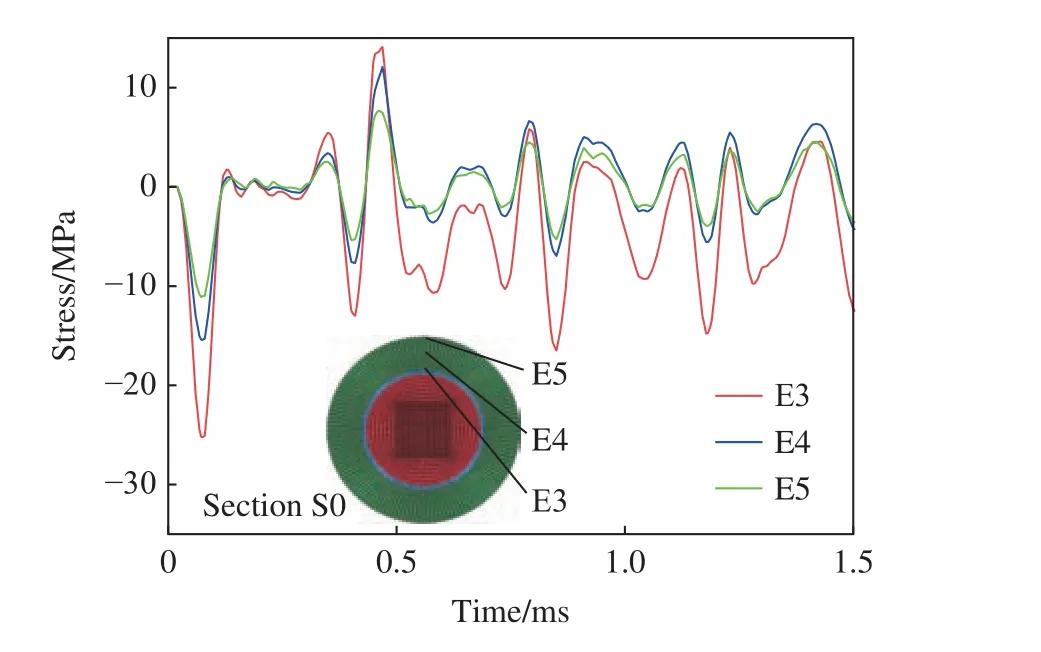
图17 滤波混凝土模型截面S0 处单元E3~E5 的应力时程曲线Fig.17 Stress time history curves of elements E3-E5 at section S0 in the filter concrete model
2.4 滤波单元参数分析
滤波单元的几何属性和材料属性对滤波混凝土在冲击荷载下的动态性能具有重要影响。在本节中对滤波单元中金属球密度、弹性层的刚度和厚度3 种参数进行分析,以研究不同参数对滤波混凝土中应力波衰减性能与储能效果的影响。对滤波混凝土模型施加峰值为10 MPa 的冲击荷载(见图10),以确保模型中各材料均处于弹性响应范围。各材料参数见表1,模型几何参数见表2。

表2 滤波单元的材料参数Table 2 Material parameters of a filter unit
图18 展示了金属球密度(ρb)分别为5 700、8 400 和11 400 kg/m3时混凝土基体的能量占比时程曲线,该占比为混凝土基体中的能量与模型总能量之比。从图18 可以看出,当金属球密度最高时,基体所存储的能量占比处于较低的范围。这说明由更重的金属球构成的滤波单元能更有效地存储冲击荷载作用于滤波混凝土中产生的能量。图19 展示了不同密度金属球所在的滤波混凝土模型中截面S4 处的平均应力时程曲线,从图19 可以看出,滤波混凝土模型中的金属球密度越高,模型中截面S4 处的峰值应力越低。这说明质量越大的金属球能更有效地衰减滤波混凝土中的应力波。
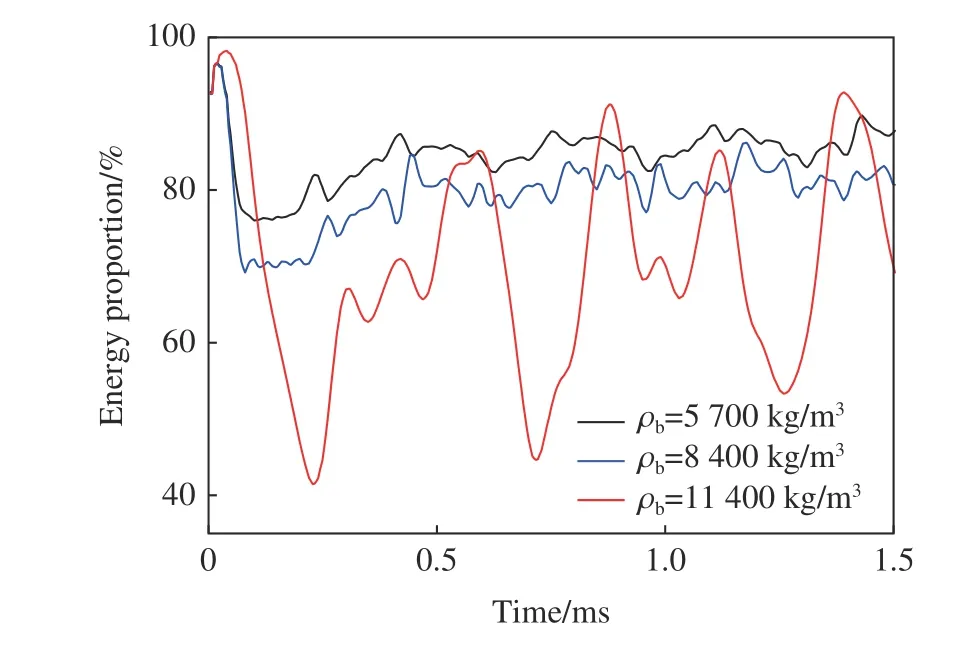
图18 金属球密度不同时混凝土基体的能量占比时程曲线Fig.18 Energy proportion time history curves of concrete matrix with different metal ball densities
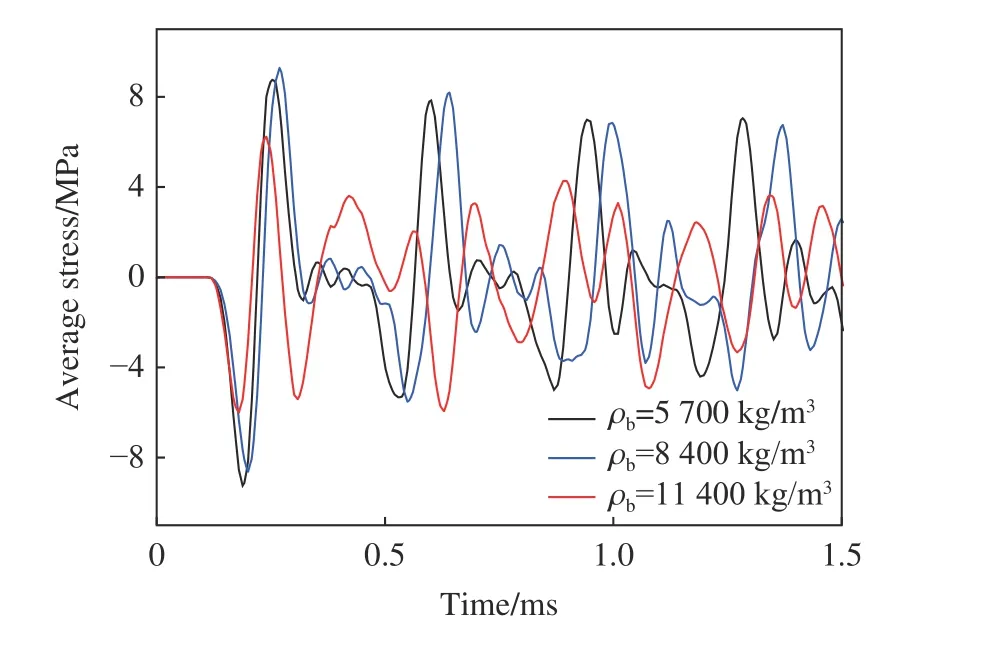
图19 金属球密度不同时截面S4 处的平均应力时程曲线Fig.19 Average stress time history curves of section S4 with different metal ball densities
图20 给出了弹性层的弹性模量E分别为4.7、47、470 和4 700 MPa 时混凝土基体的能量占比时程曲线。从图20 可以看出,当弹性层的弹性模量为47 和470 MPa 时,混凝土基体中的能量占比处于较低的范围,而过硬或者过软的弹性层都会在一定程度上提高混凝土基体中的能量,从而降低混凝土基体的抗冲击能力。图21 展示了弹性层的弹性模量不同时,滤波混凝土模型截面S0 处单元E1 和E2的位移响应曲线。通过对比可以看出,过软的弹性层会增大金属球与混凝土基体的相对位移,导致金属球的振动速度和频率大幅降低,这在一定程度上降低了弹性层对应力的传递速度以及滤波单元的储能效率。而过硬的弹性层则会限制金属球与基体之间的相对运动,在一定程度上影响滤波单元与基体之间的能量转化,从而降低滤波单元的储能效果。
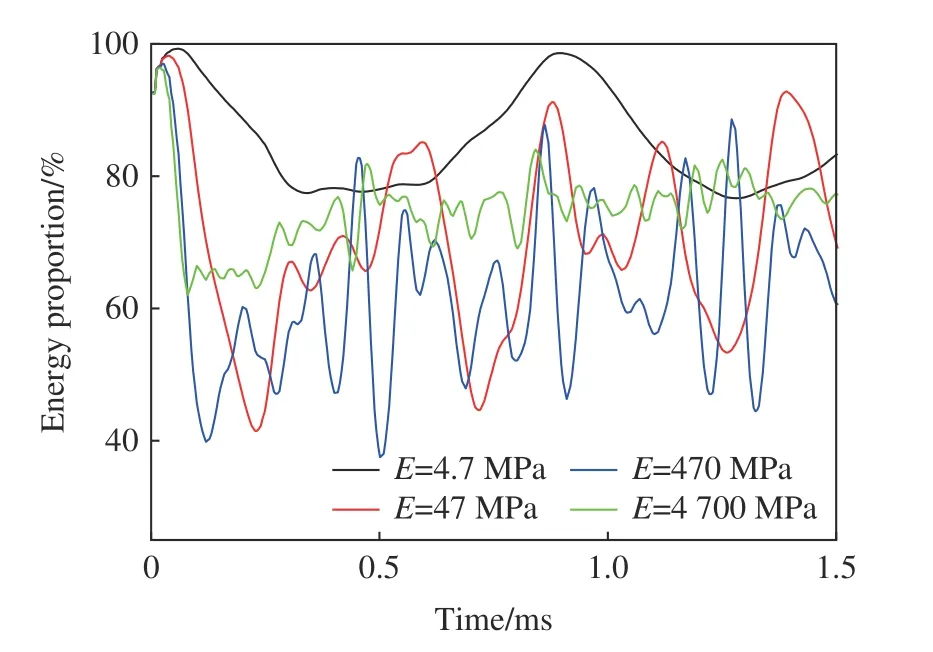
图20 弹性层的弹性模量不同时混凝土基体的能量占比时程曲线Fig.20 Energy proportion time history curves of concrete matrix with different elastic modulus of elastic layer
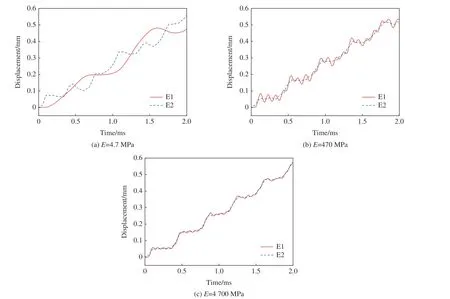
图21 弹性层的弹性模量不同时单元E1 与E2 的位移时程曲线Fig.21 Displacement time history curves of elements E1 and E2 with different elastic modulis of elastic layers
图22 给出了弹性层厚度T分别为0、1、2和4 mm 时混凝土基体的能量占比时程曲线,可以看出,当弹性层厚度为2 mm 时,混凝土基体中的能量占比处在较低的区间范围。当弹性层厚度为1 和4 mm 时,混凝土基体所存储能量的占比总体要高于弹性层厚度为2 mm 时的基体能量占比,这是因为过薄或者过厚的弹性层均会影响铅球的振动频率,从而降低滤波单元的储能效果。当金属球没有包裹弹性层时(T=0 mm),混凝土基体的能量占比处在较高的区间范围,并且具有很高的波动频率,这说明无弹性层包裹的金属球并不能有效地存储荷载中的能量。
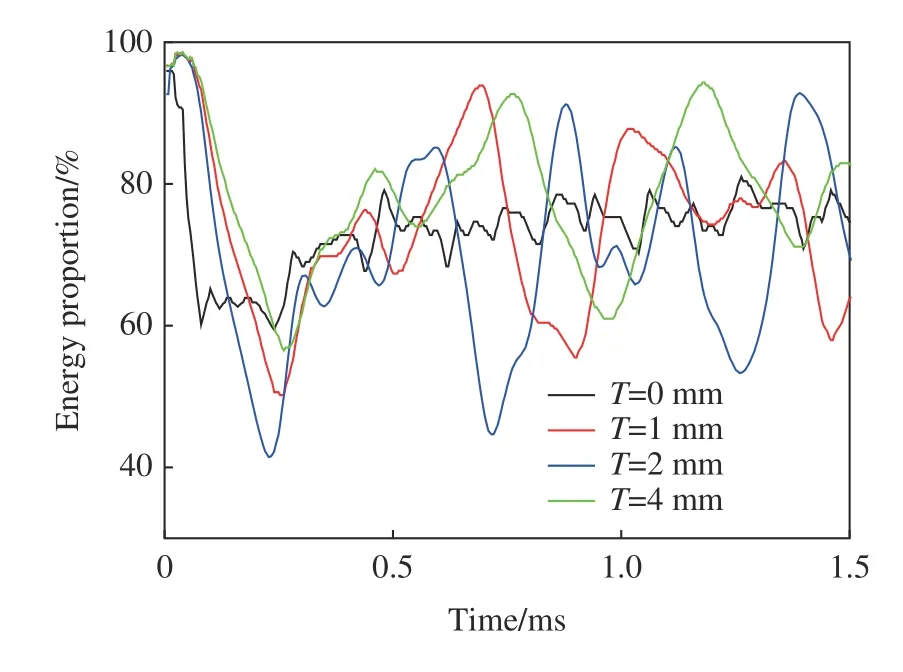
图22 弹性层的厚度不同时混凝土基体的能量占比时程曲线Fig.22 Energy proportion time history of concrete matrix with different thicknesses of elastic layers
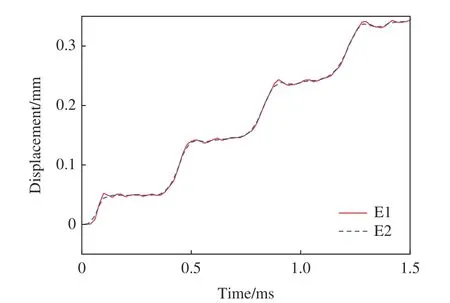
图23 无弹性包裹层时滤波混凝土模型中单元E1 与E2 的位移时程曲线Fig.23 Displacement time history curves of elements E1 and E2 without an elastic layer in the model
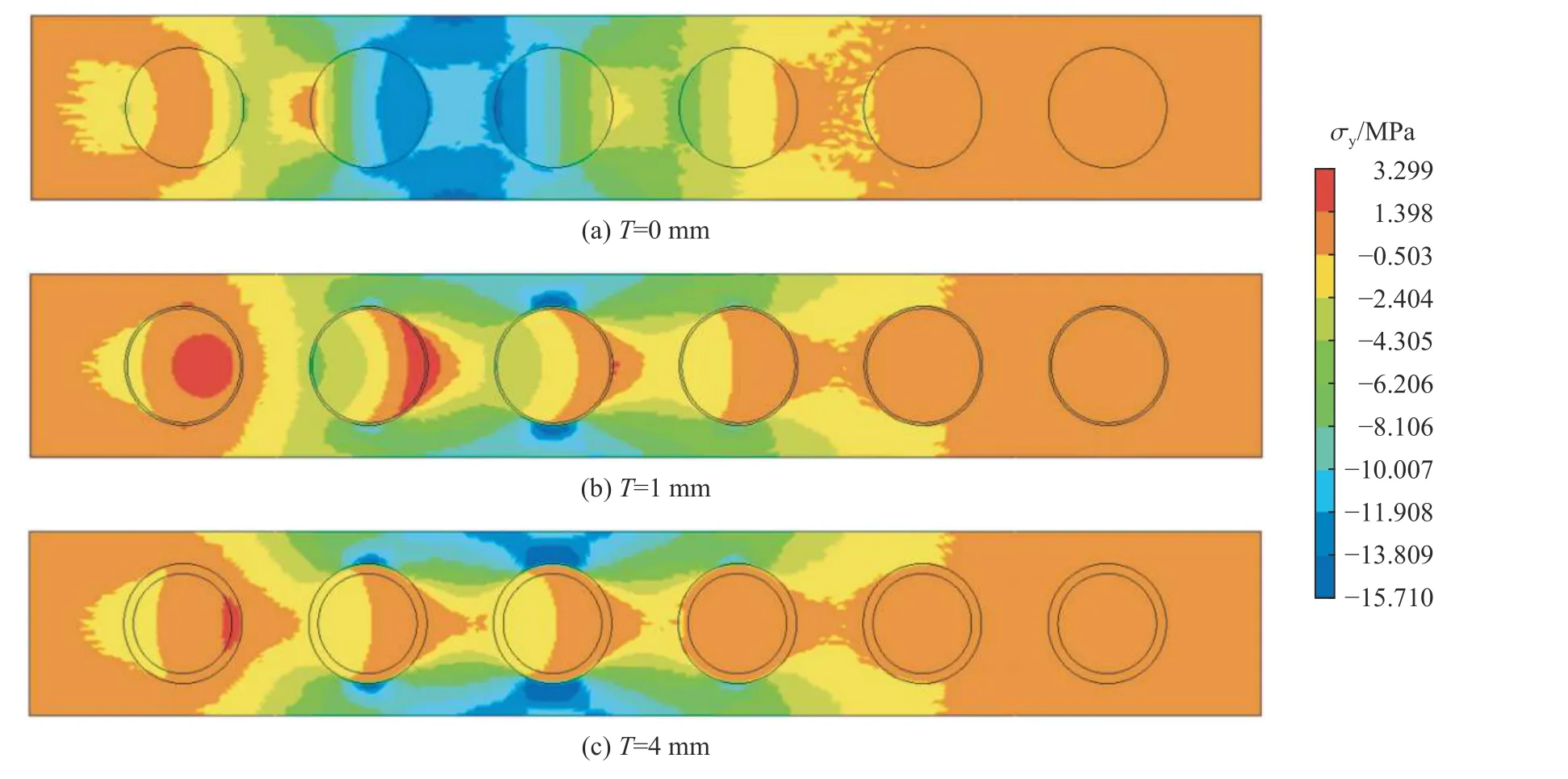
图24 具有不同厚度弹性层的滤波混凝土模型在0.120 ms 时的纵截面应力云图Fig.24 Stress contours in the longitudinal sections of the models with different thicknesses of elastic layers at 0.120 ms
3 冲击荷载作用下滤波混凝土层裂破坏数值分析
为了研究滤波混凝土在高峰值冲击荷载下的非线性响应与层裂破坏模式,如图25 所示,在模拟中对滤波混凝土模型施加峰值为40 MPa 的冲击荷载,并与相同荷载作用下的普通混凝土模型进行对比。模型的材料参数和几何参数如表1~2 所示。
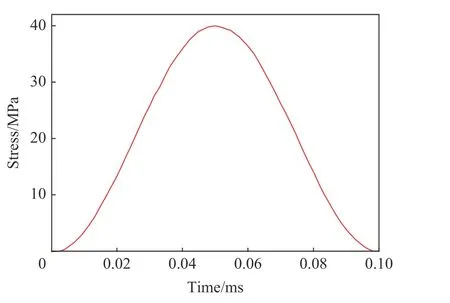
图25 峰值为40 MPa 的冲击荷载曲线Fig.25 Impact load curve with the peak value of 40 MPa
图26 展示了普通混凝土模型在峰值为40 MPa 冲击荷载作用下的层裂破坏模式,可以看出,模型在自由面附近发生了严重的层裂破坏。破坏原因是模型中的压缩应力波与反射拉伸应力波在自由面附近叠加而形成的净拉应力超过了混凝土材料的动态抗拉强度,从而导致了混凝土材料的拉伸破坏。
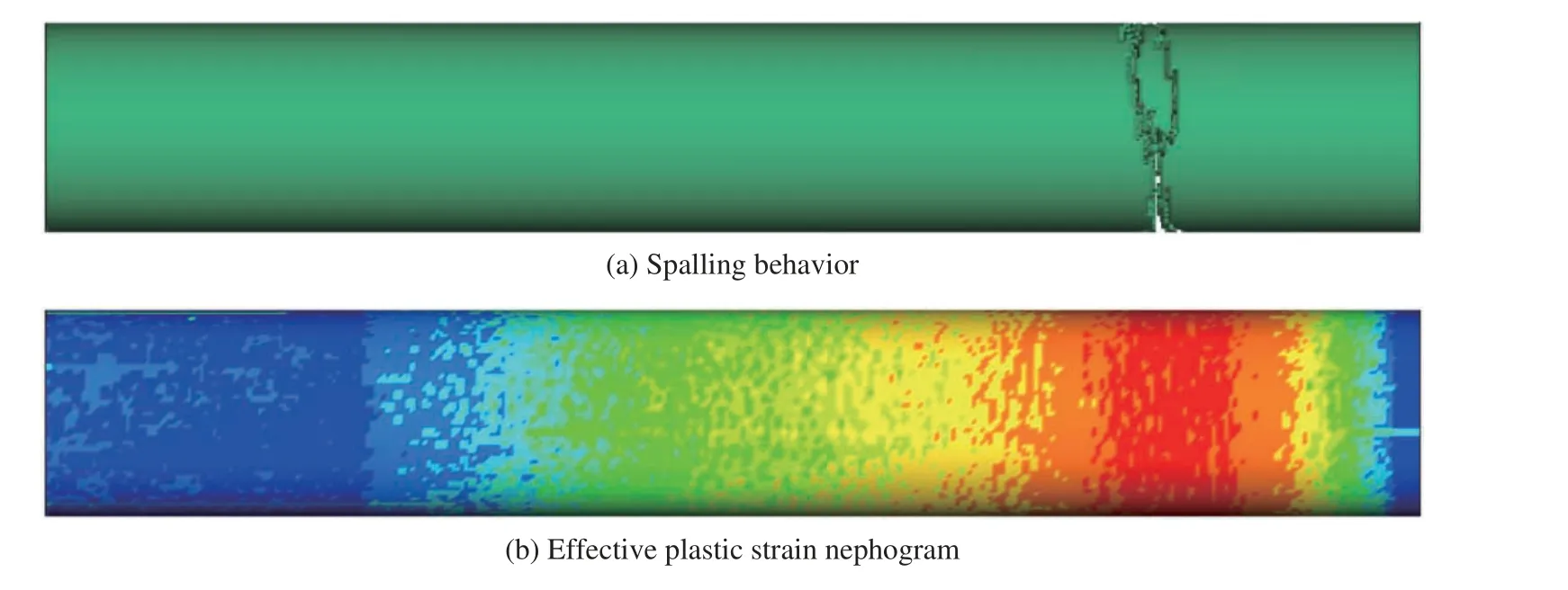
图26 普通混凝土模型的层裂破坏模式Fig.26 Spalling damage pattern of the normal concrete model
图27 展示了滤波混凝土模型在峰值为40 MPa冲击荷载作用下的层裂破坏模式,可以看出,滤波混凝土模型的中后部发生了多处层裂损伤,并且都分布在弹性层附近。在反射拉伸应力波的作用下,弹性层周围的混凝土基体中出现明显的拉应力集中现象,如图27(b)所示。由于混凝土材料的脆性和较低的抗拉强度,应力集中区域的混凝土基体很容易产生拉伸损伤,最终导致混凝土基体发生局部破坏。弹性层附近基体的局部破坏有效地吸收了冲击荷载中的能量,从而降低了滤波混凝土模型自由面附近的破坏程度。

图27 滤波混凝土模型的层裂破坏模式Fig.27 Spalling damage pattern of the filter concrete model
图28 展示了普通混凝土模型和滤波混凝土模型在峰值为40 MPa 的冲击荷载下截面S1~S4 的平均应力时程曲线。由于在模拟中考虑了混凝土材料的应变率效应,尽管压缩应力峰值超过了混凝土材料的抗压强度,模型在荷载施加面也没有发生压缩破坏。滤波混凝土模型在截面S3 处的第一压缩应力峰值为23.70 MPa(t=0.136 ms),在截面S4 处的第一压缩应力峰值为19.40 MPa(t=0.180 ms),相比于截面S1 处的第一压缩应力峰值36.90 MPa(t=0.060 ms),分别降低了35.8%和47.4%,而在普通混凝土模型中,S1~S4 截面的第一压缩应力峰值基本保持不变。当压缩应力波在自由面发生反射后,滤波混凝土模型中截面S4 的第一拉伸应力峰值为11.80 MPa(t=0.232 ms),相比于普通混凝土模型中的第一拉伸应力峰值18.79 MPa(t=0.212 ms),降低了37.2%,之后普通混凝土模型截面S4 的应力迅速降低为零,这是由于普通混凝土模型在截面S4 处发生了层裂破坏,从而导致截面所在的单元失效。
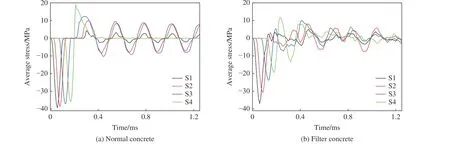
图28 峰值为40 MPa 的冲击荷载作用下各模型截面S1~S4 的平均应力时程曲线Fig.28 Average stress time history curves of sections S1-S4 of different concrete models under impact load with the peak value of 40 MPa
4 结 论
借鉴局域共振结构的设计思路,将包裹有天然橡胶弹性层的铅球均匀嵌入混凝土基体中,设计出具有应力波衰减特性的滤波混凝土。通过数值模拟方法研究了滤波混凝土模型在冲击荷载作用下的动态响应,并进行了参数分析,得到以下结论。
(1) 由弹性层与金属球组成的滤波单元有效降低了冲击荷载作用下滤波混凝土基体中应力波的传播速度与应力峰值。金属球由于弹性层的存在而与混凝土基体做相对往复运动,从而对混凝土基体的动态响应产生抑制效果。
(2) 金属球的振动与弹性层的变形使滤波单元具有很好的储能效果,从而降低了混凝土基体中的能量。在参数分析中发现,质量越大的金属球能更好地储存冲击荷载施加在滤波混凝土中的能量,从而提高了混凝土基体的抗冲击性能;弹性层的存在可以有效地提高滤波混凝土对应力波的衰减效果,但其弹性模量和厚度需要通过适当的分析来进行设计,以使滤波混凝土对应力波的衰减效果与基体中的应力达到最佳平衡。
(3) 由于较软弹性层的存在,滤波单元附近的混凝土基体出现了明显的应力集中效应,从而导致局部损伤发生。但基体的局部损伤有效地耗散了冲击荷载施加到模型中的能量,显著地降低了结构自由面附近的破坏程度。再结合滤波单元对冲击波的衰减效应,使得滤波混凝土具有良好的抗冲击性能。

