低温和低压环境下炸药爆炸冲击波的传播特性*

李 瑞，李孝臣，汪 泉，袁玉红，洪晓文，黄寅生

（1.安徽理工大学煤炭安全精准开采国家地方联合工程研究中心，安徽 淮南 232001；2.安徽理工大学化学工程学院，安徽 淮南 232001；3.南京理工大学化学与化工学院，江苏 南京 210094；4.内蒙金属材料研究所，山东 烟台 264003）

随着高效毁伤技术的不断发展以及未来战争作战条件的多元化，武器弹药适应高海拔、高空，甚至太空等极端环境的需求日益突显[1]。众所周知，高海拔或高空环境的一个重要特点就是环境温度显著低于平原地区，大气压力低于标准大气压，呈现低温和低压的环境状态。对于平原地区正常使用的常规武器弹药，在高海拔或高空等低温和低压环境使用时，炸药的爆炸能量释放受环境的影响如何，需要进行重新评估。

近年来，已有一些关于低压环境下炸药爆炸冲击波传播特性的相关研究报道。李科斌等[2]利用AUTODYN 有限元软件分析了不同真空度下爆炸近场冲击波参量的变化规律。Veldman 等[3]对不同初始环境压力下C-4 炸药爆炸冲击波的传播规律进行了数值模拟和实验研究，发现环境压力对爆炸冲击波的正反射压力和比冲量影响显著。汪泉等[4]通过抽真空爆炸系统对低压环境爆炸冲击波传播进行了实验研究，获得了不同低压条件对爆炸冲击波参量的影响规律。庞春桥等[5]和陈龙明等[6]以高海拔环境为研究背景，开展了低压条件下炸药爆炸冲击波传播的实验研究，给出了不同低压条件下炸药爆炸冲击波参量的预测公式。Izadifard 等[7]利用AUTODYN 有限元软件对高海拔环境中的低压条件对炸药爆炸冲击波传播的影响进行了数值模拟研究，拟合得到了低压条件下爆炸冲击波参量的修正因子。目前，关于高海拔环境炸药爆炸冲击波传播规律的研究主要考虑了低压条件的影响，对于低温条件，特别是高海拔、高空等的低温和低压耦合环境对爆炸冲击波传播特性的影响缺乏系统研究。

本文中，拟通过量纲分析对低温和低压环境下炸药爆炸冲击波参量进行理论分析，利用AUTODYN有限元软件开展不同低温和低压环境下炸药爆炸冲击波传播的数值模拟，探讨低温、低压和海拔高度对爆炸冲击波参量的影响。

1 爆炸冲击波参量的理论分析

1.1 爆炸冲击波参量的影响因素

炸药爆炸形成的冲击波对目标的破坏作用主要取决于冲击波正压区的特征参量，包括峰值超压Δpm、比冲量i和冲击波到达时间t等。炸药在空气中爆炸时，影响爆炸冲击波参量的物理量有炸药爆炸释放的总能量E、空气环境压力p、空气密度ρ 以及传播距离r。忽略空气介质的黏性和热传导，炸药爆炸冲击波参量可以表示为空气参数的函数形式：

1.2 爆炸冲击波参量的量纲分析

由Π 定理[8]可知，式(1)中7 个物理量有3 个基本量纲：M、L 和T，对应3 个独立的参考物理量，选择E、p和ρ 作为参考物理量，各物理量的量纲幂次如表1 所示。

对表1 进行类似矩阵初等变换，可以得到表2。

表1 爆炸冲击波传播问题中物理量的量纲幂次Table 1 Dimensional power coefficients of physical quantities in the problem of blast wave propagation

表2 爆炸冲击波传播问题中物理量的量纲幂次（初等变换）Table 2 Dimensional power coefficients of physical quantities in the problem of blast wave propagation(elementary transformation)

根据Π 定理[8]，由表2 可以得出爆炸冲击波参量峰值超压Δpm、比冲量i以及冲击波到达时间t的无量纲表达式：

对于空气，有状态方程pMr=ρRT，式中R为理想气体常数，T为环境温度，Mr为空气相对分子质量；相同炸药爆炸释放的总能量E主要取决装药质量W。因此，式(2)可以转化为：

式中：Z为比例距离，Z=r/W1/3。

从式(3)可以看出，炸药爆炸冲击波的比冲量i和冲击波到达时间t取决于环境温度T和环境压力p的影响，而爆炸冲击波峰值超压Δpm则主要取决于环境压力p的影响。

2 爆炸冲击波参量的数值模拟

2.1 计算模型

采用AUTODYN 有限元软件对球形装药的自由场爆炸冲击波传播过程进行数值模拟研究。建立如图1 所示的一维球对称楔形计算模型，模型由炸药和空气两部分组成，采用多物质Euler 算法进行数值模拟。炸药为1 kg 的TNT 球形装药，起爆方式为装药中心点起爆，在空气域边界处设置非反射边界。空气域中设置一系列观测点（P1～P24）用于爆炸冲击波特征参量的结果输出。

图1 一维球对称楔形模型Fig.1 A one-dimensional spherical symmetric wedge model

2.2 材料参数

炸药TNT 采用JWL 状态方程进行描述，具体表达式为[9]：

式中：p为爆轰产物的压力，V为爆轰产物的相对比容，A、B、R1、R2、ω 为常数，E为炸药体积内能。炸药TNT 的JWL 参数取自AUTODYN 标准材料模型库[10]。

对空气，采用理想气体状态方程描述，即：

式中：p为空气压力，γ 为理想气体绝热指数，ρ 为空气密度，e为空气的初始比内能。e取决于空气环境温度[11]：

式中：T为空气温度；cV为空气的比定容热容，理想气体的比定容热容仅取决于温度[11]。因此，以下数值模拟中，通过改变空气的初始密度和初始比内能，实现不同的低温和低压空气环境。

2.3 网格尺寸的收敛性分析

使用AUTODYN 有限元软件对不同低温和低压环境下炸药爆炸冲击波的传播过程进行数值模拟，首先需要进行网格尺寸的收敛性分析，以确定数值模型合理的网格尺寸。为此，分别采用网格尺寸为0.5、1.0、2.0、3.0、5.0 和10.0 mm 进行爆炸冲击波传播的数值模拟研究。图2 为Z=0.3, 2.0 m/kg1/3等2 种比例距离下，不同网格尺寸数值模拟得到的爆炸冲击波超压-时程曲线。

图2 不同网格尺寸的冲击波超压-时程曲线比较Fig.2 Comparison of overpressure time history curves for different cell sizes

从图2 可以看出，随着网格尺寸的增大，冲击波波峰由陡峭变得平缓，波前压力由环境压力上升至峰值压力的斜率逐渐降低，冲击波压力波形逐渐失真。对比图2 中2 个比例距离下不同网格尺寸的冲击波超压-时程曲线，可以认为网格尺寸在0.5～2.0 mm 尺寸范围内的数值模拟是收敛的。因此，为了保证数值模拟的收敛性，同时避免不必要的数值模拟计算时间，选择1.0 mm 的网格尺寸进行后续冲击波传播过程的数值模拟研究。

3 结果与分析

3.1 标准大气环境下爆炸冲击波参量

对于标准大气环境下炸药的爆炸冲击波参量已有大量的实验研究，并拟合得到了计算爆炸冲击波的峰值超压Δpm和比冲量i的经验公式[7,12-19]。这些常用的计算爆炸冲击波参量的经验公式与数值模拟和UFC 3-340-02 规范[20]的对比结果如图3 所示。从图3 可以看出，这些经验公式的适用范围和计算结果互有差异，这是由于早期的测试条件落后，仪器精度不够等多种原因导致的。

图3 标准大气环境下冲击波参量的理论、数值模拟与实验结果对比Fig.3 Comparison among theoretical, numerical and experimental blast wave parameters in standard atmospheric environment

从图3 还可以看出，不同比例距离下炸药爆炸冲击波峰值超压Δpm和比冲量i的数值模拟结果与UFC 3-340-02 规范[20]数据吻合较好，说明选择1.0 mm 的网格尺寸进行数值模拟研究是合理的。分析图3可知，对于炸药爆炸冲击波的峰值超压Δpm和比冲量i，Kinney-Grahm 公式和Izadifard-Foroutan 公式最接近UFC 3-340-02 规范[20]和数值模拟结果，相应的计算公式分别为[7,17]：

式中：Δpm和p分别为爆炸冲击波峰值超压和环境压力，kPa；i为比冲量，Pa·s；W为装药量，kg。

3.2 低温和低压环境下的爆炸冲击波参量

经验公式(7)～(8)只能描述标准大气环境下炸药爆炸冲击波的峰值超压Δpm和比冲量i，无法描述低温和低压环境下的炸药爆炸冲击波参量变化规律。为此，结合量纲分析推导的关系式(3)，根据相似准则对式(7)～(8)进行整理，可以得到描述低温和低压环境下炸药爆炸冲击波峰值超压Δpm和比冲量i的计算公式分别为：

式中：ph和p0分别为低压环境和标准大气环境下的环境压力，kPa；下标h为海拔高度，m；Th和T0分别为低压环境和标准大气环境下的环境温度，K；W为装药量，kg。

为了验证式(9)～(10)预测低压环境下炸药爆炸冲击波超压和比冲量的准确性，选择Th=20 ℃，ph=p0, 2p0/3,p0/3 进行理论计算和数值模拟研究，并与实验数据[21]进行对比。相应的爆炸冲击波峰值超压Δpm和比冲量i的理论计算、数值模拟与实验数据对比结果如图4 所示。

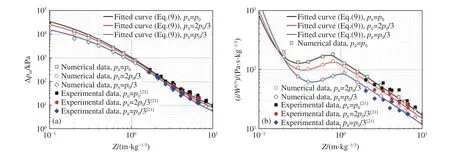
图4 低压环境下冲击波参量的理论、数值模拟与实验数据对比Fig.4 Comparison among theoretical, numerical and experimental shock wave parameters in diminished pressure environments

从图4 可以看出，不同环境压力下冲击波参量的理论计算结果与数值模拟及实验结果吻合较好，说明式(9)～(10)和数值模拟能够较好地预测低压环境下炸药爆炸冲击波的峰值超压Δpm和比冲量i。分析图4(a)可知，爆炸冲击波的峰值超压随着环境压力的降低而减小，爆炸近场的冲击波峰值超压下降幅度要大于爆炸远场。对于图4(b)，当Z＜0.2 m/kg1/3时，爆炸冲击波的比冲量随着环境压力的降低而略有增大；当Z＞0.2 m/kg1/3时，冲击波比冲量随着环境压力的降低而减小。

同样，为了验证式(9)～(10)预测低温环境下爆炸冲击波峰值超压和比冲量的准确性，选择环境压力ph=101.325 kPa，环境温度Th=20, -18, -53 ℃进行理论计算和数值模拟研究。相应的爆炸冲击波峰值超压Δpm和比冲量i理论计算、数值模拟和实验数据的对比结果如图5 所示。

图5 低温环境下冲击波参量的理论、数值模拟结果与实验结果的对比Fig.5 Comparison among theoretical, numerical and experimental shock wave parameters in diminished temperature environments

从图5 可以看出，不同环境温度下爆炸冲击波参量的理论计算、数值模拟与实验数据吻合较好，说明式(9)～(10)和数值模拟能够较好地预测低温环境下炸药爆炸冲击波的峰值超压Δpm和比冲量i。分析图5 可知，环境温度对爆炸冲击波的峰值超压Δpm影响不大，但影响爆炸冲击波的比冲量i，冲击波比冲量i随环境温度降低而增大。

3.3 高海拔环境下的爆炸冲击波参量

高海拔环境是典型的低温和低压耦合大气环境，高海拔环境下环境温度和大气压力与海拔高度分别有如下关系[7,22]：

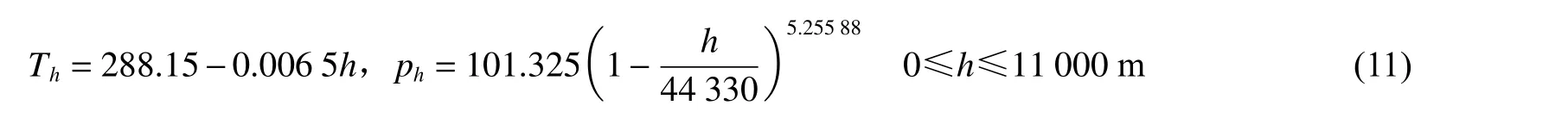
根据关系式(11)和空气状态方程pMr=ρRT，计算获得不同海拔高度h下的环境温度Th、环境压力ph和空气密度ρh，如表3 所示。

将表3 中不同海拔高度下的环境温度Th和环境压力ph代入式(5)～(6)，计算获得不同海拔高度下的空气状态参数，再利用AUTODYN 有限元软件对不同海拔高度下炸药爆炸冲击波的传播过程进行数值模拟研究。同时，将表3 中不同海拔高度下的大气参数代入式(9)～(10)，计算获得不同海拔高度下的爆炸冲击波峰值超压Δpm和比冲量i。相应爆炸冲击波参量的理论计算、数值模拟与实验数据对比结果，以及冲击波超压Δpm和比冲量i随海拔高度h增加的变化率如图6 所示。

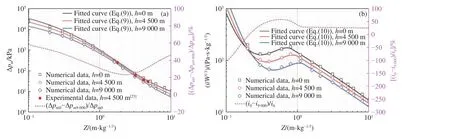
图6 高海拔环境下冲击波参量的理论、数值模拟结果与实验结果的对比Fig.6 Comparison among theoretical, numerical and experimental shock wave parameters in high-altitude environment

从图6 可以看出，不同海拔高度下爆炸冲击波参量的理论计算与数值模拟、实验结果吻合较好，表明式(9)～(10)能够较好地预测高海拔的低温和低压耦合大气环境下炸药爆炸冲击波的峰值超压Δpm和比冲量i。分析图6(a)可知，爆炸冲击波的峰值超压Δpm随海拔的升高而降低，海拔从0 m 升至9 000 m时，冲击波峰值超压降低23.5%～58.2%，平均降低了35.3%。因此，海拔高度在0～9 000 m 范围内，海拔每升高1 000 m，冲击波峰值超压平均降低约3.9%。对于图6(b)，Z＜0.2m/kg1/3时，爆炸冲击波的比冲量i随海拔的升高而增大，海拔从0 m 升至9 000 m 时，冲击波比冲量i增大0.8%～94.8%，平均增大了43.2%；当Z＞0.2 m/kg1/3时，爆炸冲击波的比冲量随海拔的升高而减小，海拔从0 m 升至9 000 m 时，冲击波比冲量i减小4.9%～58.8%，平均减小了28.4%。因此，海拔高度在0～9 000 m 范围内，Z＜0.2 m/kg1/3时，海拔高度每升高1 000 m，比冲量i平均增大约4.8%；Z＞0.2 m/kg1/3时，海拔每升高1 000 m，比冲量i平均减小约3.2%。对比图4～6 可知，炸药爆炸冲击波的峰值超压Δpm随海拔的升高而减小，主要是由低压环境导致的，环境温度影响不大。Z＜0.2 m/kg1/3时，爆炸冲击波比冲量i随海拔的升高而增大，是由低压和低温条件共同促进作用导致的。Z＞0.2 m/kg1/3时，爆炸冲击波比冲量i随海拔的升高而减小，说明低压条件对冲击波比冲量的减弱作用大于低温条件的促进作用。综上分析，高海拔环境的低压和低温条件对爆炸冲击波参量有重要影响。相比于低温条件，高海拔环境下低压条件对爆炸冲击波参量的影响程度更高。

3.4 冲击波波阵面运动规律

Dewey[24]通过实验数据拟合得到了标准大气环境下1 kg 球形TNT 装药的爆炸冲击波传播轨迹经验公式：

式中：r为爆炸冲击波半径，m；A=0.055 963，B=1.017 51，C=-0.454 03 和D=2.055 27 为拟合系数；a0=340.292 m/s 为标准大气条件下的空气音速；t为爆炸冲击波的传播时间，s。

式(12)只能描述标准大气环境下1 kg TNT 装药的爆炸冲击波传播轨迹，不能描述低温和低压环境下不同装药量的爆炸冲击波传播过程。为此，根据式(3)和相似准则，对式(12)进行整理，得到低温和低压环境下装药量为W的炸药爆炸冲击波传播轨迹计算公式：

式中：Ds为冲击波传播速度，m/s。

通过数值模拟过程中监测点位置及冲击波的超压-时程曲线，可以追踪得到爆炸冲击波波阵面的运动轨迹。不同低压和低温条件下炸药爆炸冲击波传播轨迹的理论计算、数值模拟与实验结果的比较如图7 所示。从图7 可以看出，不同低压和低温环境下炸药爆炸冲击波波阵面的运动轨迹理论计算结果与数值模拟、实验结果吻合较好，说明式(13)能够较好地预测低压和低温环境下炸药爆炸冲击波波阵面的运动轨迹。分析图7 可知，对于相同的传播时间，爆炸冲击波的传播距离随环境压力的降低而增大，随环境温度的降低而减小。表明环境温度和环境压力对爆炸冲击波的传播速度都有重要影响。

通过式(14)可以计算获得不同低温和低压条件下炸药爆炸冲击波的传播速度，如图8 所示。从图8可以看出，大气环境压力降低，爆炸冲击波的传播速度升高，而大气环境温度降低，爆炸冲击波的传播速度降低。因此，图7 中炸药爆炸冲击波的传播距离随环境压力的降低而增大，随环境温度的降低而减小。由图8 可知，随着传播时间的延长，冲击波传播速度逐渐衰减，最终衰减为空气的音速。由于空气的音速主要取决于环境温度[22]，进而图8 中低压环境下爆炸冲击波的传播速度衰减趋于同一值（见图8(a)），低温环境下爆炸冲击波传播速度衰减趋于不同值（见图8(b)）。

图7 不同低压和低温环境下爆炸冲击波波阵面的运动轨迹Fig.7 Motion trajectories of blast wave in diminished pressure and temperature environments

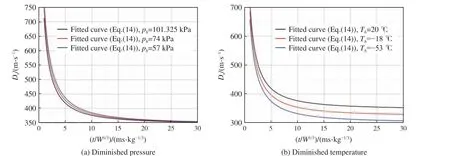
图8 不同低压和低温环境下爆炸冲击波的传播速度Fig.8 Propagation velocities of blast waves in diminished pressure and temperature environments

对于高海拔的典型低温和低压耦合环境，将表3 中不同海拔高度下环境温度Th和环境压力ph代入式(5)～(6)，结合空气状态方程获得不同海拔高度下的空气状态参数，再利用AUTODYN 有限元软件对不同海拔高度下爆炸冲击波传播过程进行数值模拟研究。同时，将表3 中不同海拔高度下大气参数代入式(13)～(14)，计算获得不同海拔高度下爆炸冲击波运动轨迹和传播速度。不同海拔高度下爆炸冲击波波阵面运动轨迹和冲击波传播速度的理论计算、数值模拟与实验结果的对比如图9 所示。

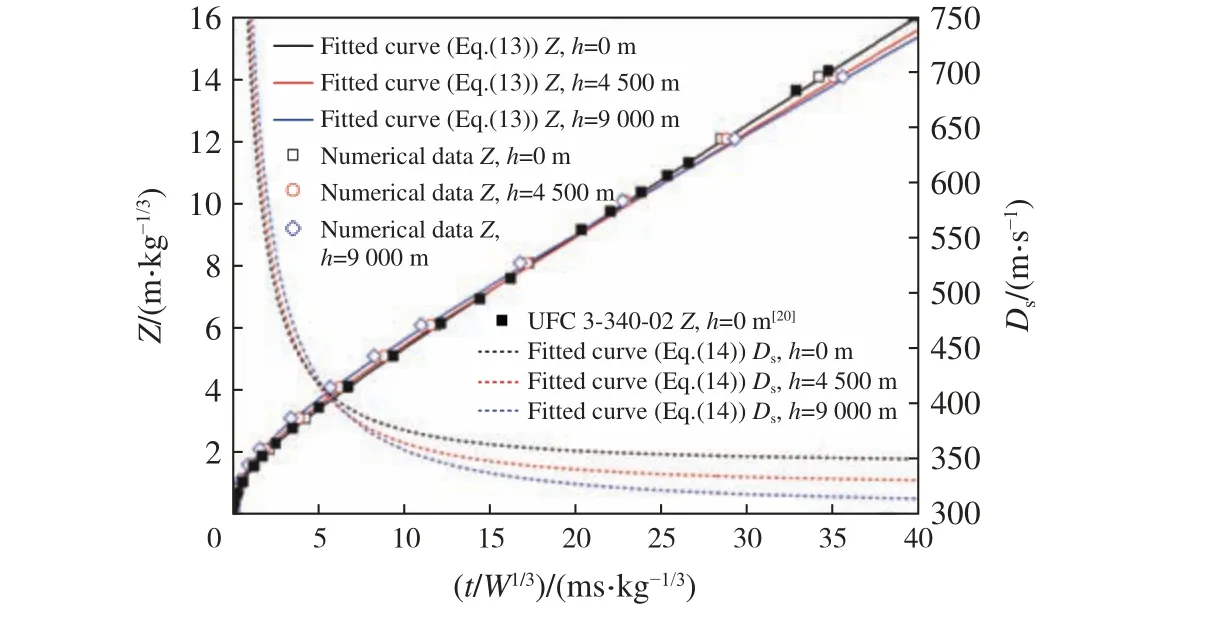
图9 不同海拔高度下爆炸冲击波波阵面运动轨迹及传播速度的理论、数值模拟结果与实验结果的对比Fig.9 Theoretical, numerical and experimental comparison of shock wave parameters in different high-altitude environments

从图9 可以看出，不同海拔高度下炸药爆炸冲击波波阵面运动轨迹的理论计算结果与数值模拟、实验结果吻合较好，表明式(13)可以较好地预测不同海拔高度下炸药爆炸冲击波波阵面的运动轨迹。分析图9 可知，对于爆炸近场（Z＜8 m/kg1/3），相同的传播时间内，炸药爆炸冲击波的传播距离随海拔的升高而增大，对于爆炸远场（Z＞10 m/kg1/3），爆炸冲击波的传播距离随海拔的升高而减小。这是由于爆炸近场的冲击波传播速度随海拔的升高而升高，爆炸远场冲击波传播速度随海拔的升高而降低导致的（图9 中不同海拔高度下的爆炸冲击波传播速度）。综合分析图7～9 可知，高海拔环境下炸药爆炸冲击波的传播速度，对于爆炸近场主要取决于低压环境的影响，而对于爆炸远场主要取决于低温环境的影响。

4 结 论

基于量纲分析理论和AUTODYN 有限元软件，对不同低温、低压和高海拔条件下炸药爆炸冲击波的峰值超压、比冲量和波阵面运动轨迹等参量进行了理论分析和数值模拟，并与实验数据进行了对比验证，得到了不同低温和低压环境下炸药爆炸冲击波参量的变化规律，主要结论如下。

(1)通过量纲分析理论结合标准大气环境下冲击波参量经验公式，建立了预测低温和低压环境下炸药爆炸冲击波峰值超压、比冲量和波阵面运动轨迹的计算公式，并通过数值模拟和实验数据验证计算公式的预测准确性。

(2)大气环境参数影响着炸药爆炸冲击波参量，环境压力降低，爆炸冲击波的峰值超压和爆炸远场（Z＞0.2 m/kg1/3）比冲量减小，冲击波传播速度升高。环境温度降低，炸药爆炸冲击波的比冲量增大，传播速度降低，峰值超压影响不大。

(3)海拔高度在0～9 000 m 范围内，每升高1 000 m 冲击波峰值超压和爆炸远场比冲量分别平均降低约3.9%和3.2%。爆炸近场的冲击波传播速度随海拔的升高而升高，爆炸远场的冲击波传播速度随海拔的升高而降低。高海拔环境下低压条件对峰值超压和比冲量的影响程度高于低温条件，爆炸近场冲击波的传播速度主要取决于低压的影响，爆炸远场冲击波的传播速度则主要取决于低温的影响。