爆破中双线型聚能药包最佳成缝角度*

尤元元，崔正荣，张西良，游 帅，康一强，肖成龙，鲁非相

（1.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083；2.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；3.中钢集团马鞍山矿山研究总院股份有限公司，安徽 马鞍山 243000）

预裂爆破能够合理利用和有效控制炸药能量，较边坡开挖主爆区的炮孔先起爆，提前形成一条贯通裂缝，以减少爆炸应力波对保留岩体的损伤效应的新技术，已成为了露天矿维护边坡稳定中的重要手段之一。相对于普通爆破，预裂爆破后边坡成型质量有较大提升，但边坡损伤、超欠挖问题仍较严重，边坡半壁孔率不高[1]。

针对上述工程现状，大量学者进行了相关研究并取得了丰富的研究成果。线型聚能药包是实现预裂爆破的新思路，从1983 年Rustan 把聚能装药结构引入岩石爆破，并在此基础上提出了线型聚能装药爆破方法后，此技术在我国也得到了广泛地推广并做了很多研究工作[2]。罗勇等[3]通过矩形线型切割器模型试验和现场试验获得了线型聚能结构药包用于定向断裂时岩石裂纹的产生及扩展过程。刘文革等[4]提出了轴对称线型聚能拉伸爆破技术，通过模型试验和数值模拟轴对称聚能药包均达到了较好的聚能效应，为轴对称聚能药管设计奠定了坚实的理论和实验基础。但这些技术仅对岩石定向断裂有重要指导意义，未能从微观机理角度进行相关分析。杨仁树等[5]、宋俊生等[6]以数值模拟与现场试验为手段，研究了线型聚能药包炸药爆轰过程岩体全场的应力场分布。梁洪达等[7]通过对双向聚能拉伸破岩机理进行分析，建立了多种聚能爆破模式下围岩应力和应力叠加方程。这些微观机理的研究对线型聚能爆破有重要指导意义，但未能从提高线型聚能药包做功能力角度进行研究。赵建平等[8]通过灰色关联分析理论，认为影响线型聚能药包做功能力的典型参数从大到小依次为：聚能方向夹角、聚能锥角、装药量、爆心距、岩体质量和炮孔深度。吴波等[9]基于光滑粒子流体动力学方法（SPH）研究了外壳和药型罩对椭圆双极线性聚能药包做功能力的影响，认为外壳厚度一定时，药型罩厚度越小，聚能药包做功能力越强。黄风雷等[10]采用脉冲X 光照相及威力效应实验，提出了通过小炸高、大锥角来提高聚能药包的侵彻能力。薛宪彬[11]认为直径28 mm 的煤矿许用炸药，对称双线型聚能槽聚能张开角为65°时，双线型聚能结构在聚能方向聚能效应最佳。

上述研究成果虽然在聚能爆破和线型聚能爆破机理及应用方面取得了显著进展，但对双线型聚能结构药包有效聚能炸药边界方程的研究还停留在最小二乘法估算，并且针对聚能结构最佳聚能张开角研究还很模糊，并且局限于相关文献的近似取值。本文在对双线型聚能结构药包有效聚能炸药边界方程理论推导的基础上，利用Python 语言调用SymPy 包对隐函数进行可视化，求解不同聚能张开角条件下具体的有效聚能炸药边界方程，得出不同聚能张开角条件下的炸药聚能效应有效利用率，进而得出聚能槽方向的线型聚能效应最大时的聚能张开角，并通过数值模拟、物理模型试验和现场试验及应用对不同双线型聚能张开角对预裂孔成缝规律和聚能射流侵彻过程进行研究。

1 理论分析

1.1 双线型聚能药包爆破原理

对于普通圆柱型药包爆破机制，应力波动态和爆生气体准静态共同作用理论为大多数研究者所认同。即在炮孔周围由于冲击波的作用形成粉碎区，随着应力波的传播在粉碎区以外产生裂隙区，随后爆生气体的气楔作用，裂隙区不断向外扩展，由于应力波的衰减最终在炮孔远区形成振动区。而对于双线型聚能结构药包爆炸时，如图1 所示，炸药的总能量不变，聚能槽的存在使得能量重新分配，靠近聚能槽方向的炸药能量由于聚能槽的影响，使能量会往聚能槽方向聚集，双线型聚能爆破形成的高压力、高速度、高密度的能量射流能够提高炸药爆炸的做功能力。双线型聚能结构药包爆破是指，在震源药柱的轴向表面对称设置两条直线型聚能槽，使震源药柱在轴向两侧形成线型聚能射流。

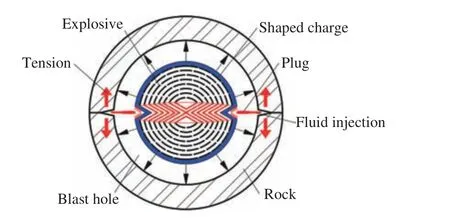
图1 双线型聚能爆破能量示意图Fig.1 Schematic diagram of the energy in bilinear shaped charge blasting

震源药柱的爆速约为4 500 m/s，所以可以近似的认为震源药柱的爆轰是在瞬时完成的。假设爆轰产物的体积等于装药的初始体积，产物的质点初速度为零。炸药爆炸所释放出的能量全部转化为爆轰产物的内能，飞散时内能完全转变为动能，并对被爆介质做功。沿圆面和锥角面两个方向层层向外飞散的爆炸产物会在炸药内部相遇，形成交界面[12-14]。

1.2 装药爆炸分析模型的建立

聚能张开角是影响聚能射流形成的典型结构参数，确定最佳的聚能张开角度，进而计算出炸药产生聚能效应的最大有效利用率，能够优化双线型聚能装药结构，提高双线型聚能爆破效果和炸药能量的利用率。炸药起爆后，散射面一层层向外传播，具体传播过程如图1 所示，这样沿两个方向飞散的爆生产物在中间形成一个临界面，求出这条曲线可以求出炸药产生聚能效应的有效利用率。由于双线型聚能药包是中心对称结构，为简化计算量，以直径为45 mm 震源药柱为研究对象，聚能张开角顶到炸药断面圆心的距离OH=15 mm，在第一象限建立函数模型，如图2所示。

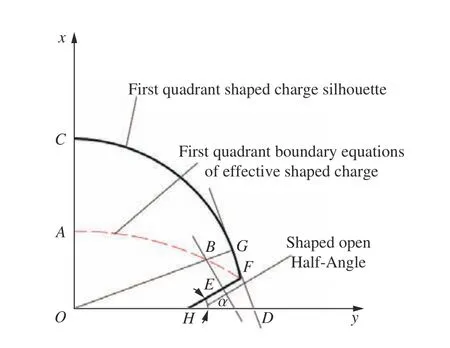
图2 第一象限药柱炸药利用率函数模型Fig.2 Functional model of explosive utilization ratio in the first quadrant

设聚能张开角半角为 α ；炸药断面半径为r；曲线AF为有效聚能炸药边界；B为有效聚能炸药边界上任意一点，坐标为 (x0,y0) ；G为炸药断面边界轮廓上的一点，且与OB在同一直线，其坐标为 (x1,y1) ；E为直线FH上的一点，且BE⊥FH，坐标为 (x2,y2) ，直线FH在x轴的截距为15 mm。

圆第一象限的函数式为：

直线FH的函数式为：

直线BG的斜率kBG为：

直线BE的斜率kBE为:

设G(x0,y0) 为有效聚能炸药边界上的一点，则根据瞬时爆轰假说，该点到圆的距离BG和到直线FH的距离BE相等[15]：

联立上述三个方程可得出，关于G(x0,y0) 的隐函数方程式，也就是双线型聚能方向的有效聚能炸药边界方程。

SymPy 是基于Python 的科学计算包，用于处理方程和方程组的求解、多项式求值、积分和微分方程、计算极限、级数展开和级数求和、矩阵运算、简化表达式、寻找微分方程和微分方程组的解。本文利用SymPy 包求解隐函数方程，并将隐函数方程可视化[16]，得到不同聚能张开角有效炸药边界，如图3所示。

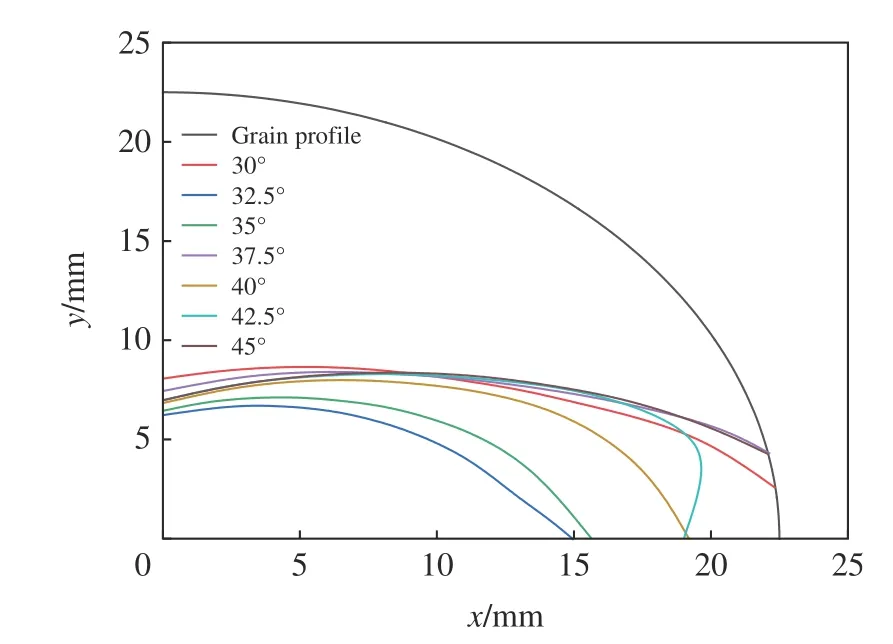
图3 不同聚能张开半角有效聚能炸药边界方程Fig.3 Boundary of effective shaped charge to the relative half opening angle

根据不同有效聚能炸药边界方程进行积分，可以得到有效聚能炸药面积，计算得到炸药产生聚能效应有效利用率 γ ：

通过对每一个有效利用率 γ 进行计算，得出不同聚能张开角下的炸药产生聚能效应有效利用率如图4 所示，可知，聚能张开角为75°时聚能效应的有效利用率（41.32%）与聚能张开角为60°的聚能效应有效利用率（40.53%）相近。

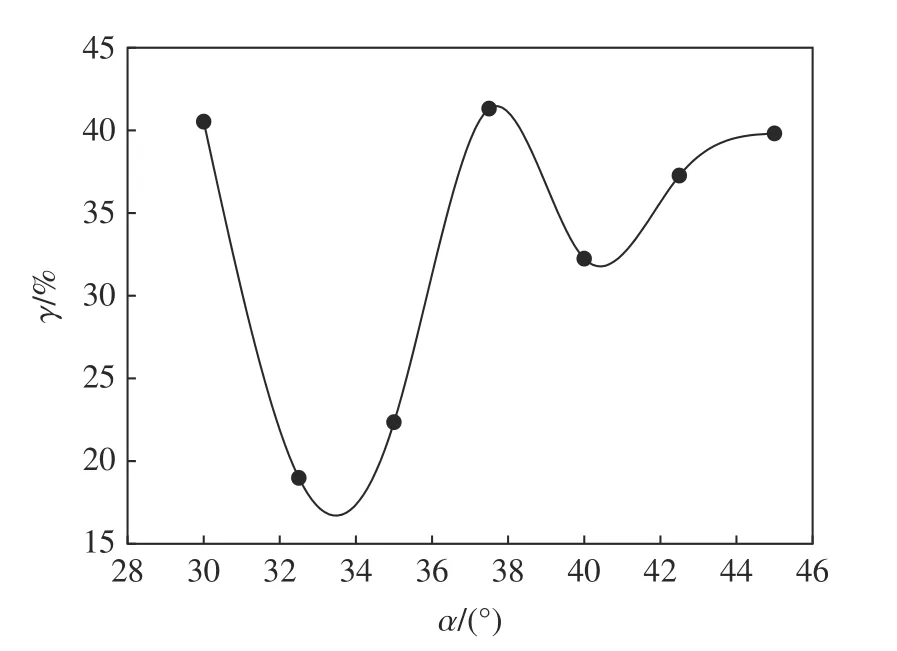
图4 不同聚能张开半角炸药聚能效应有效利用率Fig.4 Efficiency of shaped charge (γ) to the relative half opening angle (α)

2 模型试验

2.1 试验结构及材料

2.1.1 药包装药结构

试验所用聚能药包药型结构由紫铜压制而成，在紫铜管围成空腔内装填炸药，并在铜管端头连接雷管。紫铜具有良好的延展性、柔韧性、易加工且工程造价低，故试验采用紫铜管作为聚能结构药包材料。试验炸药采用混有40%石膏的黑索金，炸药性能参数如表1 所示。装药结构经抽压装置压制而成，所用紫铜管外径6 mm，内径5 mm，管壁厚0.5 mm，由于结构直径限制，聚能张开角存在一定误差，但在可控范围之内。特别说明，同普通圆柱状药包比较，依据1.2 节理论最终确定设计聚能槽角度分别为60°和75°两种聚能张开角度。三种装药结构如图5 所示。

表1 炸药性能参数Table 1 Explosive performance parameters

图5 装药结构Fig.5 Charge structure

2.2 单孔有机玻璃预试验

为了验证水泥砂浆模型试验选取的炸药和聚能结构药包合理性，开展了小药量普通圆柱状和对称双线型聚能结构药包有机玻璃侵彻预试验。由于有机玻璃的透明特性，可以直观的观察爆破后的侵彻作用，同时证明对称双线型聚能结构药包产生聚能效应的可靠性，为进行双孔水泥砂浆试验提供参考。

2.2.1 有机玻璃预试验方案

预试验材料选用100 mm×100 mm×100 mm、中心钻孔为8 mm 的有机玻璃，如图6(a)所示。圆柱形药包和聚能张开角为双线型结构药包填装混有40%石膏的黑索金，具体试验爆破参数如表2 所示。药包一端与雷管底部用爆破专用胶带与雷管连接。置于炮孔时，用塑料泡沫对药包结构高度及聚能槽方向进行定位，具体有机玻璃模型设置过程如图6 所示。

表2 试验爆破参数Table 2 Test parameters

图6 有机玻璃模型设置过程Fig.6 PMMA model setup process

2.2.2 有机玻璃侵彻试验结果

在有机玻璃侵彻试验后，普通圆柱状药包试验结果如图7(a)所示，有机玻璃上无明显的定向侵彻裂纹，侵彻裂纹呈在各个方向呈放射状。对称双线聚能药包的试验结果如图7(b)所示，对称双线型聚能结构药包在炮孔两侧形成明显的定向侵彻裂纹，证明对称双线型聚能装药结构能够形成了聚能效应。有机玻璃上的侵彻缝与炮孔中心有一定的偏离，由于试验过程中角度固定的原因，致使侵彻缝偏离。因此对称双线性聚能装药结构产生的定向聚能效果在误差允许的范围内达到了预期的试验效果。

图7 药包侵彻结果Fig.7 Results of charge package infiltration

2.3 双孔水泥砂浆模型试验

2.3.1 水泥砂浆试块

所用约束立方体盒子尺寸400 mm×400 mm×200 mm。采用425#水泥、铁钢砂、河沙、水按照1∶1∶0.3∶0.4 的质量比例制作爆破模型试块，为满足试件强度要求养护三个月，如图8 所示。经试验测得试件静态力学参数结果如表3 所示。

图8 水泥砂浆试块Fig.8 Cement mortar test block

表3 水泥砂浆试件静态力学参数Table 3 Static mechanical parameters of cement mortar

2.3.2 试验过程分析

在水泥砂浆试块中心线位置设计孔径10 mm，孔深100 mm，药包填装混有40% 石膏的黑索金2.435 g。普通圆柱状药包孔距为80 mm，聚能张开角为60°的双线型聚能结构药包孔距为80 mm，聚能张开角为75°的双线型聚能结构药包孔距为100 mm。药包一端与雷管底部用爆破专用胶带与雷管连接。置药包于炮孔时，用塑料泡沫对药包结构高度及聚能槽方向进行定位，并同时起爆，具体物理模型设置过程如图9 所示。

图9 物理模型设置过程Fig.9 Physical model setup process

2.3.3 试验结果分析

从图10 试件爆后效果图可以看出圆柱装药结构和聚能张开角为60°的双线型聚能装药结构，在相同药量和孔距条件下，圆柱药包仅在炮孔连线方向形成一条弯曲主裂缝，在炮孔连线方向上下侧形4 条翼裂纹，聚能张开角为60°的双线型聚能装药结构在炮孔连线方向形成一条主裂缝，炮孔连线方向没有翼裂纹产生。

图10 试件爆后效果Fig.10 Effect after the test piece exploded

在同等药量下，与聚能张开角为60°的双线型聚能结构相比，聚能张开角为75°的双线型聚能结构药包孔距增大至100 mm，爆后在炮孔连线方向上形成一条贯穿主裂缝，炮孔方向没有翼裂纹的产生，并且聚能张开角为75°的双线型聚能结构药包聚能爆破效果明显优于聚能张开角为60°的双线型聚能结构药包。

图11 可以看出爆破后炮孔口均出现小范围的爆破漏斗，为雷管引爆时雷管爆炸作用力所致。图11(a)圆柱型药包结构爆破后除在炮孔连线方向形成了一条未贯穿主裂缝，主裂缝方向与炮孔连线方向成10°。图11(b) 双线型聚能结构药包聚能张开角为60°，两炮孔侧面形成两条与炮孔连线方向成8.5°的牵手裂缝并贯通。图11(c)可以看出双线型聚能结构药包聚能槽张开角为75°，炮孔两侧形成两条分别与炮孔连线方向成5°和5.3°的牵手裂缝，没有翼裂纹产生，并且与聚能槽为60°的聚能结构药包相比，增大孔距的同时成缝效果更加显著。

图11 试件局部损伤Fig.11 Local damage of specimens

3 单孔双线型聚能数值模拟

3.1 模型建立

为进一步研究聚能张开角对双线型聚能结构药包聚能效果的影响，利用LS-DYNA 非线性有限元软件建立三维计算模型。模型是建立在无限体假设基础上的平面应力问题，建立模型的同时必须考虑模型尺寸以及划分网格的数量问题，模型的尺寸越大，需要划分的网格相对越多，计算量也就越大，同时模型边界如果为自由面，那么由于反射而形成的拉伸波又会对无限体模型带来影响[17]。该模型为1/4 对称准静态模型，模型主体的尺寸长100 cm，宽100 cm，厚度为0.1 cm，炮孔直径为90 cm，药柱直径为4.5 cm，双线性聚能结构厚度为0.2 cm，聚能槽顶点位置距药包中心1.5 cm，聚能结构聚能槽张开角分别为60°、65°、70°、75°、80°。在z方向设置法向约束，在对称轴上分别设置对应的对称边界条件，由于实际岩体可看作无限大，为了防止建模时在岩体边界处产生应力波的反射作用，在岩石x、y边界上设置无反射边界条件。图12 双线型聚能物理模型，图13 为数值计算模型。

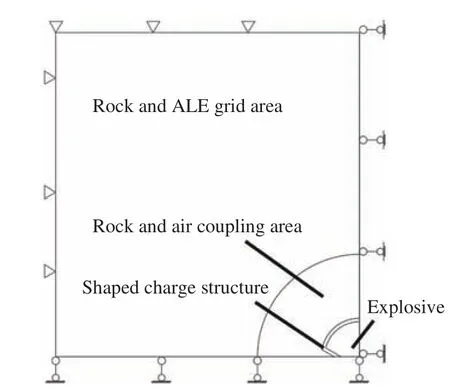
图12 双线型聚能物理模型Fig.12 Physical model of bilinear shaped charge

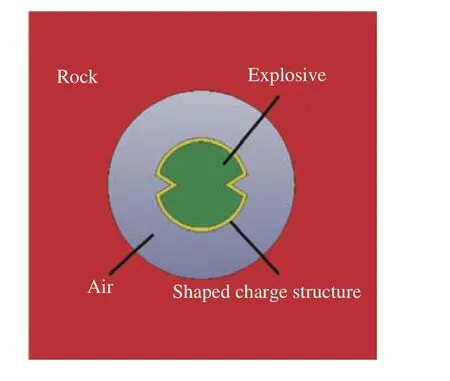
图13 数值计算模型Fig.13 Numerical calculation model

3.2 数值模拟本构模型及参数选取

LS-DYNA 包含了多种材料模型，可以用来模拟爆破下岩石的损伤演化。本研究中选用RHT 材料模型如表4 所示，该模型能够表征高应变率爆炸荷载下的岩体行为。它是一种适用于混凝土、岩石等脆性材料的塑性模型。文献表明[18-20]，RHT 材料模型能够成功地纳入非线性岩石特性。

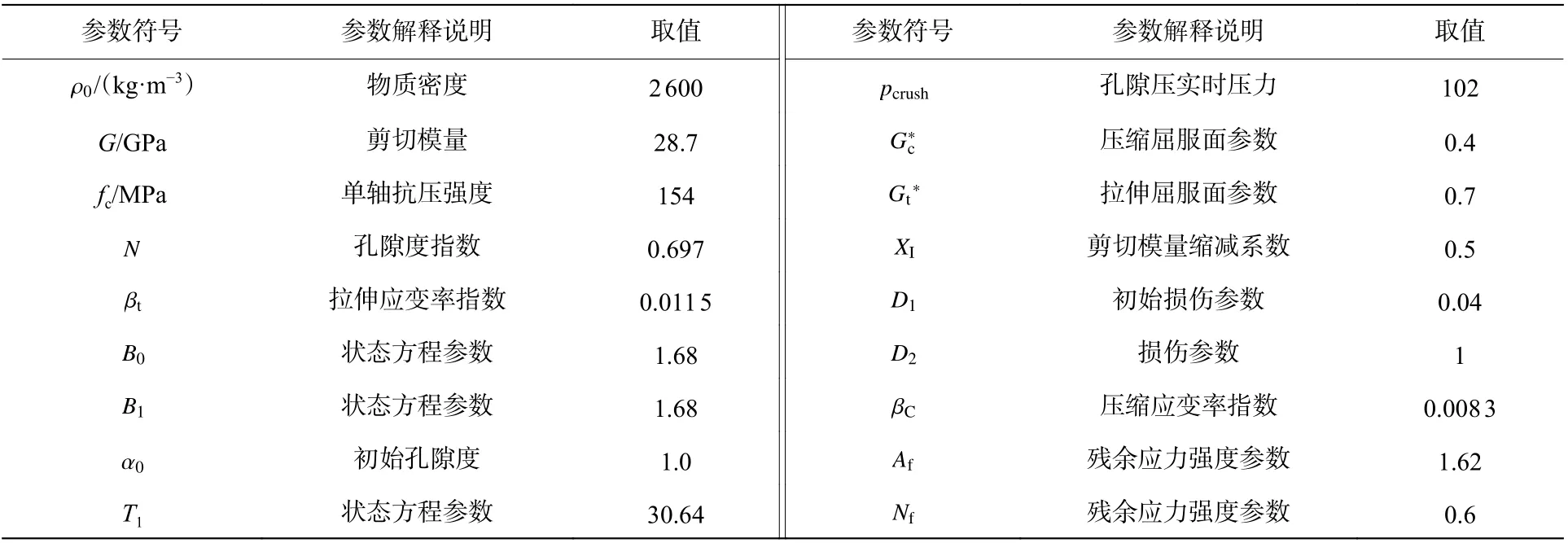
表4 岩石材料参数Table 4 Rock material parameters

本文炸药本构模型选用LS-DYNA 自带的*MAT_HIGH_EXPLOSIVE_BURN 模型，爆轰产物的 JWL状态方程选用适当的参数定量描述爆轰产物的压力与体积变化关系：

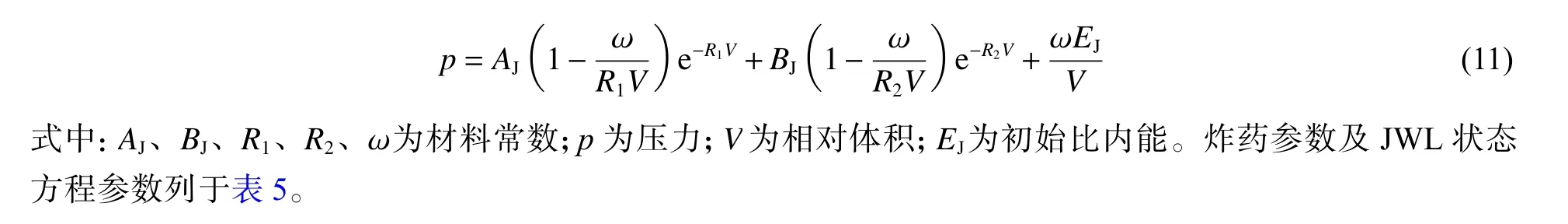
表5 炸药及其状态方程参数Table 5 Explosive and its state equation parameters

聚能结构的主要作用是将炸药的爆炸能量转换成聚能结构的动能，用几乎不可压缩的金属射流替代可压缩的气体射流，来提高聚能药包的聚能威力。选取的材料可压缩性要小、密度要大、塑性和延展性要好、在形成射流过程中不会产生汽化。本文聚能管材料选用红铜，模型关键字为：*MAT_PLASTIC_KINEMATIC。其具体材料参数见表6。

表6 聚能管材料参数Table 6 Shaped tube material parameters

3.3 岩石侵彻分析

图14～图18 给出了不同开张角下的岩石被侵彻过程的von Mises 应力云图。可以看出，双线型聚能装药结构在不同聚能张开角的工况下，12 µs 炸药爆后产生的应力波作用在双线型聚能结构药包上，18 µs 双线型聚能结构药包形成聚能射流并与炸药分离，16 µs 聚能射流均达到炮孔壁岩石单元，并产生应力集中，随着聚能射流的向前运动，爆轰波通过炮孔壁向外传播，岩石开始发生侵彻，20 µs 聚能射流完成对岩石的侵彻作用，侵彻深度达到最大。20 µs 时，通过对比分析五种不同聚能张开角工况的Mises 应力云图，可以得出聚能张开角为75°时，岩石的侵彻深度最深而且聚能槽方向的应力集中效应最为显著，对称双线性聚能装药结构聚能效应达到最佳。

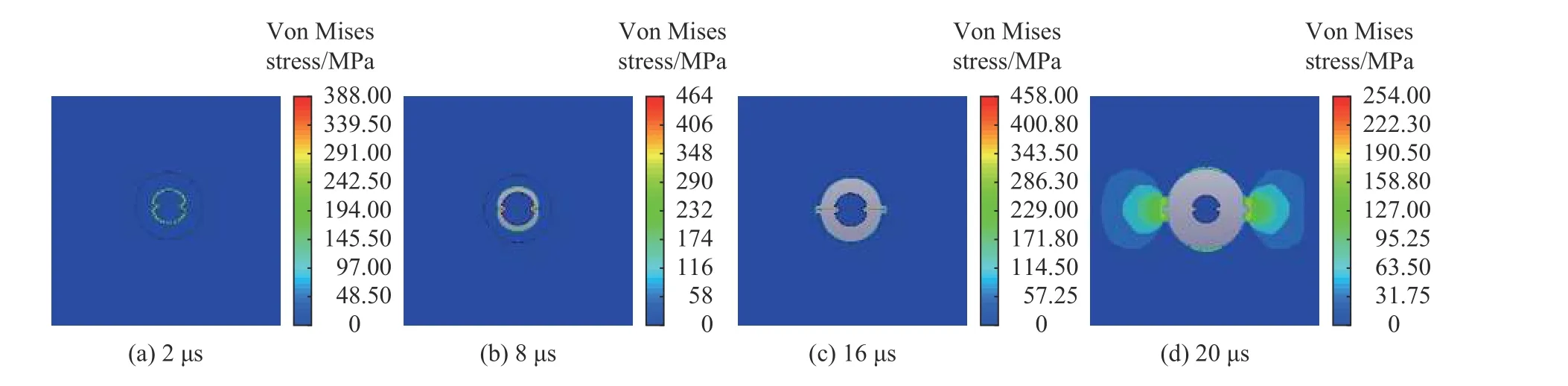
图14 张开角为60°的侵彻过程von Mises 应力云图Fig.14 Von Mises stress contour diagram of penetration process with an opening angle of 60°

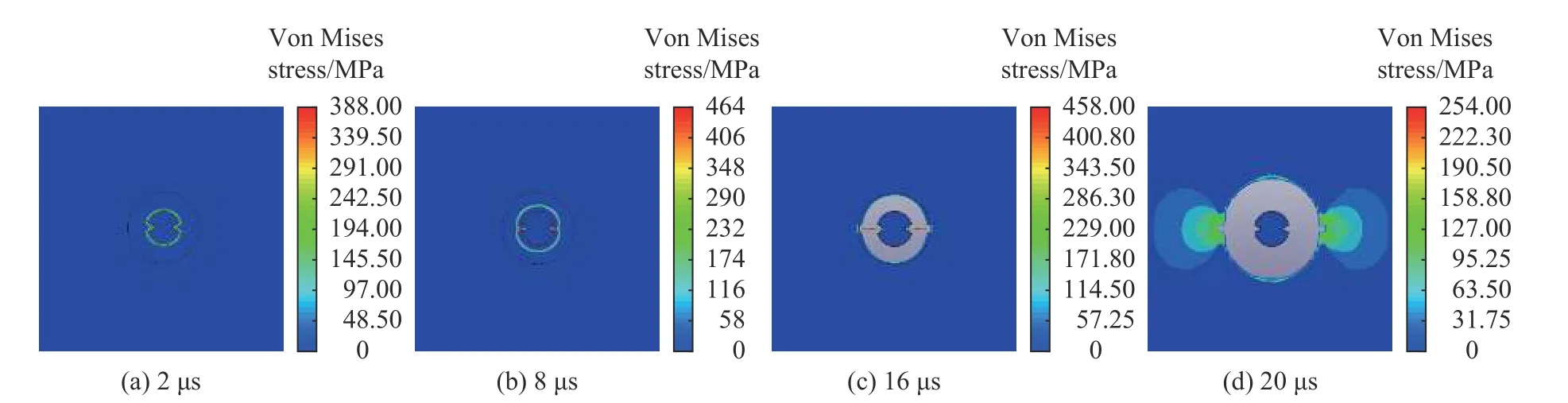
图15 张开角为65°的侵彻过程von Mises 应力云图Fig.15 Von Mises stress contour diagram of penetration process with an opening angle of 65°

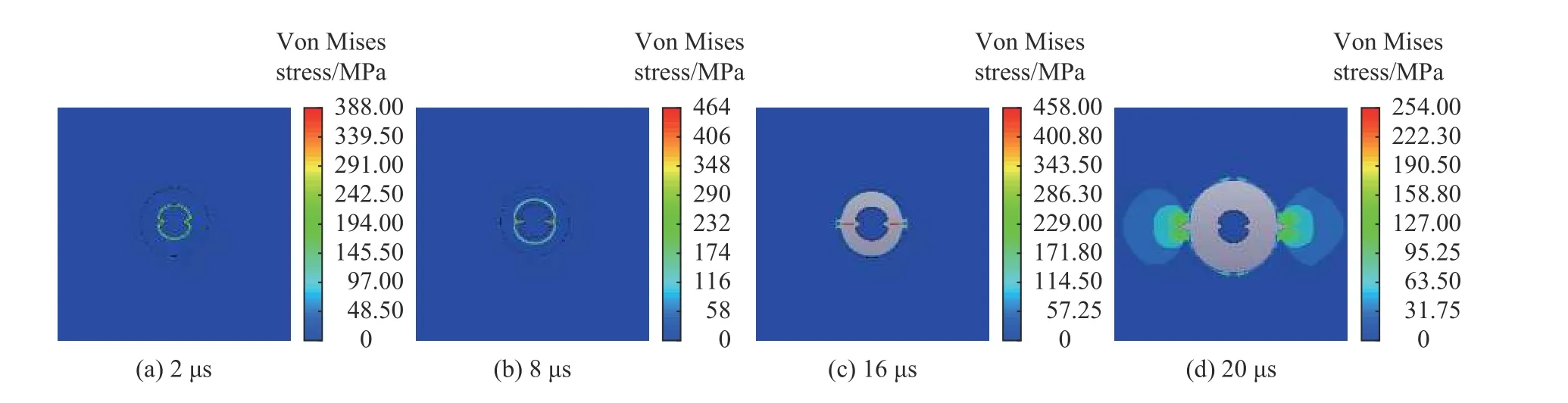
图16 张开角为70°的侵彻过程von Mises 应力云图Fig.16 Von Mises stress contour diagram of penetration process with an opening angle of 70°

图17 张开角为75°的侵彻过程Mises 应力云图Fig.17 Von Mises stress contour diagram of penetration process with an opening angle of 75°

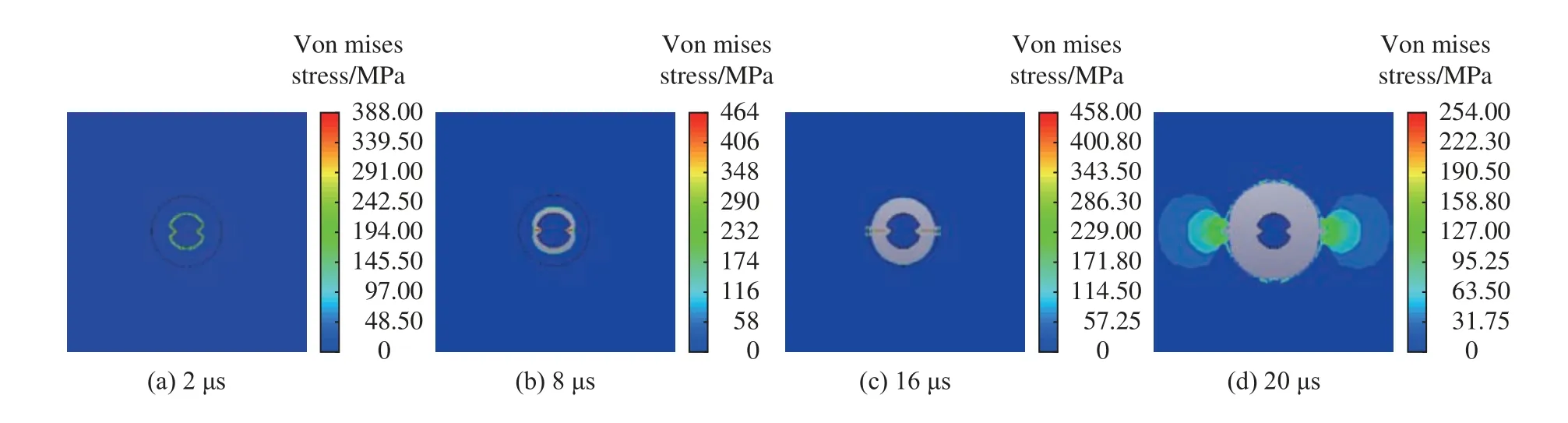
图18 张开角为80°的侵彻过程von Mises 应力云图Fig.18 Von Mises stress contour diagram of penetration process with an opening angle of 80°

3.4 聚能方向炮孔壁岩石单元应力分析

为具体研究不同聚能张开角对双线型聚能药包聚能效果的影响，分别取聚能张开角为60°、65°、70°、75°和80°炮孔连线方向炮孔壁上的岩石单元H33925，具体位置如图19 所示，通过分析该单元的应力时程曲线，得出不同聚能张开角下在选取时间范围内（10～30 µs）岩石单元H33925 应力时程曲线，如图20 所示。炸药起爆后，针对不同聚能张开角工况，由于聚能射流的作用下，岩石单元H33925 总体趋势都是在一定时间内达到应力峰值，随后应力逐渐衰减。但是不同聚能张开角的工况下，岩石单元H33925 到达应力峰值的时间不同，聚能张开角为75°的岩石单元在19 µs 最先达到峰值应力，并且与60°、65°、70°和80°对应的岩石单元H33925 的应力峰值相比，聚能张开角为75°的岩石单元H33925 的应力峰值最大为2 121.5 MPa。因此，不同聚能张开角的工况下，聚能张开角为75°的炮孔连线方向炮孔壁岩石单元H33925 最先达到峰值，并且应力峰值最大，即沿聚能槽方向的线型聚能效应最大。

图19 炮孔壁岩石单元H33925Fig.19 Rock unit H33925 at blast hole wall

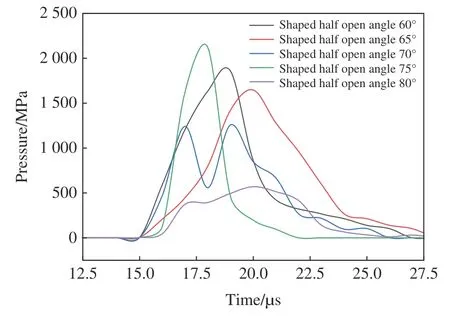
图20 不同聚能张开角岩石单元H33925 应力时程曲线Fig.20 Stress-time history curves of rock element H33925 with different shaped opening angles

通过对双线型聚能结构药包有效炸药边界方程进行理论推导，并利用Python 语言调用SymPy 包对隐函数进行可视化，求解出30°、32.5°、35°、37.5°、40°、42.5°、45°聚能张开半角具体的有效聚能炸药边界方程，得出聚能张开半角为37.5°时，聚能效应有效利用率最大为41.32%，即沿聚能槽方向的线型聚能效应最大。针对炸药聚能效应有效利用率相近的聚能张开角60°、75°进行双孔水泥砂浆模型试验，试验结果表明聚能结构药包聚能槽张开角为75°与60°相比，聚能结构药包聚能槽张开角为75°的成缝效果更加显著。通过数值模拟对聚能槽张开角分别为60°、65°、70°、75°、80°的Mises 应力云图进行分析，得出聚能张开角为75°时，岩石的侵彻深度最深而且聚能槽方向的应力集中效应也最佳。

4 现场工程应用试验

4.1 工程背景

为进一步验证理论分析、数值模拟及物理模型试验结果的可靠性，针对不同岩性对比分析常规预裂爆破和聚能张开角为75°的双线型聚能结构药包的预裂爆破效果，选取西北某露天矿板岩和白云岩两个典型岩性爆区进行现场试验。

4.2 试验爆破参数设计

露天深孔预裂爆破预裂孔装药不耦合系数一般为2～4，并根据两个典型岩性爆区的地质条件，双线型聚能爆破孔和普通爆破孔的直径均为120 mm，药包的直径约为45 mm，具体炸药性能参数如表7 所示。两个典型岩性爆区的台阶高度H1均为12 m，常规预裂爆破孔的板岩孔距为1 m、白云岩孔距为1.2 m。在理论分析、数值模拟及物理模型试验分析的基础上，双线型聚能预裂爆破孔的板岩孔距增大20%设计为1.2 m、白云岩孔距增大20%设计为1.44 m，常规和双线型聚能预裂爆破板岩和白云岩具体爆破参数设计见表8。

表7 炸药性能参数Table 7 Explosive performance parameters

表8 预裂爆破参数( H 1=12 m )Table 8 Pre-split blasting parameters ( H 1=12 m )

4.3 双线型聚能结构的现场装药

现场试验采用由PVC 管、张开角为75°的紫铜聚能槽制成的双线型聚能结构药包如图21(a)所示，PVC 管、聚能槽PVC 管等长为2 m 一段，用相同直径开缝PVC 管为套管，在此基础上进行现场组装如图21(b)所示。利用套管连接的同时并用透明胶带进行二次连接，如图21(c)所示。为保证聚能管位于预裂孔中心，用与聚能管结构相切的炮孔弦长等长度的三个竹竿进行聚能结构定位，使聚能槽方向正对预裂孔连线方向，如图21(d)所示。

图21 现场组装过程Fig.21 On-site assembly process

4.4 试验结果分析

普通预裂爆破爆破后，特别是在板岩碎裂岩区，预裂面半孔率仅为40%，边坡底部存在超挖、预裂面伞岩挂壁及被爆破岩体的损伤严重，不利于后期边坡的稳定及维护，增加维护成本的同时存在安全隐患，如图22 所示。聚能张开角为75°的双线型聚能结构药包预裂爆破爆破后，预裂面在板岩和白云岩孔距增大20%的条件下，现场试验效果良好，半孔率达到90%，坡底无超挖欠挖现象，预裂面干净整洁无伞岩挂壁现象，如图23 所示。对被保护岩体的损伤较小有利于边坡的稳定，在一定程度上减少后期边坡的维护费用，节约了边坡维护及预裂爆破成本，提高预裂爆破循环作业效率。

图22 常规预裂爆破效果Fig.22 Effects of conventional pre-split blasts

图23 双线型聚能预裂爆破Fig.23 Effects of bilinear shaped pre-split blasts

5 结 论

(1) 建立双线型聚能爆破药柱装药利用率计算模型，利用Python 语言调用SymPy 包对隐函数有效炸药边界方程进行可视化，求解出60°、65°、70°、75°、80°、85°、90°不同聚能张开角第一象限对应的有效聚能炸药边界方程。得出不同聚能张开角下的炸药产生聚能效应有效利用率，当聚能张开角为75°时，聚能效应有效利用率最大为41.32%，即沿聚能槽方向的线型聚能效应最大。

(2) 同等药量与圆柱型药包相比，聚能张开角为60°和75°的聚能结构药包，在炮孔连线方向均能形成完整定向裂缝。同等药量增大孔距20%的条件下，聚能结构药包的聚能槽张开角为75°的聚能效果明显优于聚能槽张开角为60°的聚能结构药包。

(3) 通过建立数值计算模型，对双线型聚能结构聚能张开角为60°、65°、70°、75°、80°五种工况进行数值模拟，结果表明聚能张开角75°时，炮孔连线方向炮孔壁上岩石单元最先达到应力峰值，且应力值最大为2 121.5 MPa。

(4) 对聚能张开角为75°的双线型聚能结构药包开展了爆破现场试验，结果表明板岩和白云岩两种不同岩性在孔距增大20%的条件下，双线型聚能预裂爆破的半孔率达到90%优于常规的预裂爆破的半孔率。