波形控制器对杀伤战斗部破片飞散特性影响研究*

刘 伟，梁争峰，阮喜军，屈可朋

（西安近代化学研究所，陕西 西安 710065）

杀伤战斗部利用炸药爆炸产生的能量驱动破片高速飞散，对飞机、导弹等空中目标进行毁伤[1]。传统的圆筒形杀伤战斗部在起爆后，两端和中心位置的破片飞散速度差异较大，在动态弹目交汇条件下，两端的破片容易脱靶，并且战斗部破片飞散角较大，破片沿轴向分布范围较大，沿目标方向分布密度较小，达不到预期的毁伤效果[2-4]。因此，改善杀伤战斗部破片的飞散特性十分重要[5]。

控制战斗部破片飞散特性的主要方法是改变战斗部的起爆方式、装药曲线和长径比等[6-7]。李松楠等[8]通过数值计算方法研究了起爆点位置对杀伤战斗部破片飞散角的影响，结果表明，在中心起爆时，适当减小起爆点与装药底端的距离可以提高破片的初速，减小破片的飞散角；张绍兴等[9]基于Shapiro 公式设计了3 种不同曲率半径的战斗部壳体曲线，通过数值计算方法研究了壳体形状对破片飞散特性的影响，得到了壳体曲率半径增大、破片初速提高、破片飞散角增大的结论；Dhote 等[10]对长径比分别为0.8、1.2 和1.8 的3 种杀伤战斗部进行了破片飞散试验，结果表明，起爆方式相同时，长径比越大，破片飞散角越大。近年来，有学者提出使用波形控制器改变爆轰波波形，从而控制杆条破片的飞散状态。张会锁等[11]对有波形控制器作用下的杆条破片战斗部的杆条初始抛撒状态进行了数值计算，结果表明，波形控制器能改变爆轰波波形，使爆轰波能量均匀地作用于杆条上，使杆条在初始飞散时受力均匀，变形弯曲减小。但与杆条不同的是，破片杀伤战斗部需要更精确地对破片的飞散方向进行控制。

本文中拟通过在主装药与破片之间增加波形控制器的方法控制破片飞散方向，改善破片飞散特性，并基于爆轰波在惰性材料中的反射理论和Shapiro 公式设计波形控制器形状；并通过数值计算和试验验证该方法的合理性，分析对比有无波形控制器以及波形控制器选择不同材料时对破片飞散速度和破片飞散角的影响规律。

1 波形控制器设计

1.1 破片飞散角概念

战斗部破片飞散特性主要包括破片飞散速度和破片空间分布，破片空间分布通过破片飞散角表示。如图1 所示，破片飞散角是指战斗部爆炸后，在战斗部轴向平面内，以质心为顶点所做的包含90%有效破片的角度，即破片飞散图中包含90%有效破片的两线之间的夹角[12]。破片飞散角越小，目标方向上的破片分布密度越大，对目标的毁伤效应越明显，因此战斗部破片飞散角是衡量杀伤战斗部威力的重要参数之一[13]。

图1 破片飞散角示意图Fig.1 Schematic diagram of fragment scattering angle

1.2 波形控制器曲线设计

波形控制器具有可压缩性，当爆轰波在传播过程中遇到波形控制器边界时，会使波形控制器材料发生变形，而变形会显著地影响爆轰波的传播状态。爆轰波在界面处反射，在爆轰产物中形成反射爆轰波，并在波形控制器中形成斜冲击波。如图2 所示，OA为入射爆轰波，OR为反射爆轰波，OB为透射冲击波[14]。

图2 爆轰波在波形控制器界面上的反射与透射Fig.2 Reflection and projection of detonation wave on wave shape controller interface

爆轰波阵面OA后的CJ 面参数满足以下关系：

式中：γ 为绝热指数，ρ0为炸药密度，D为炸药爆速，pH为炸药爆轰流场压力，ρH为炸药爆轰流场密度，cH为炸药爆轰流场声速，uH为炸药爆轰流场爆速。

联立式（11）～（16）可求解出爆轰波在波形控制器中透射的斜冲击波与界面的夹角 φ3和冲击波在波形控制器中的传播速度。然后结合Shapiro 公式，由数值拟合的方法得到波形控制器曲线。Shapiro 公式为：

图3 Shapiro 公式计算示意图Fig.3 Shapiro formula calculation diagram

图4 波形控制器曲线设计示意图Fig.4 Schematic diagram of wave shape controller curve design

所设计的杀伤战斗部长度为200 mm、直径为160 mm，结合以上方法设计了波形控制器材料为尼龙、战斗部飞散角理论值为10°的波形控制器模型，如图5 所示。

图5 波形控制器模型示意图Fig.5 Schematic diagram of wave shape controller model

2 数值模拟

2.1 数值计算模型

采用SOLIDWORKS 软件建立杀伤战斗部有限元模型，并使用HyperMesh 软件划分网格。采用LS-DYNA软件计算杀伤战斗部的破片飞散过程，并采用LS-Prepost 后处理软件进行分析。建立的杀伤战斗部数值计算模型如图6所示，该模型由不锈钢壳体、铝合金前后端盖、波形控制器、HMX 主装药，800 枚立方体预制钢破片和空气组成，外形尺寸与第1 节中设计的杀伤战斗部原理样机相同，破片尺寸为10 mm×10 mm×10 mm。使用ALE（arbitrary Lagrange-Euler）算法建模，壳体、前后端盖、波形控制器和破片采用Lagrange 网格，主装药和空气采用Euler 网格，使用多物质流固耦合算法进行计算，该方法可以降低Lagrange 与Euler网格相互作用出现网格畸变的概率。空气网格边界施加压力外流边界条件，以模拟无限大空气域，防止压力在边界反射影响破片飞散特性的计算。

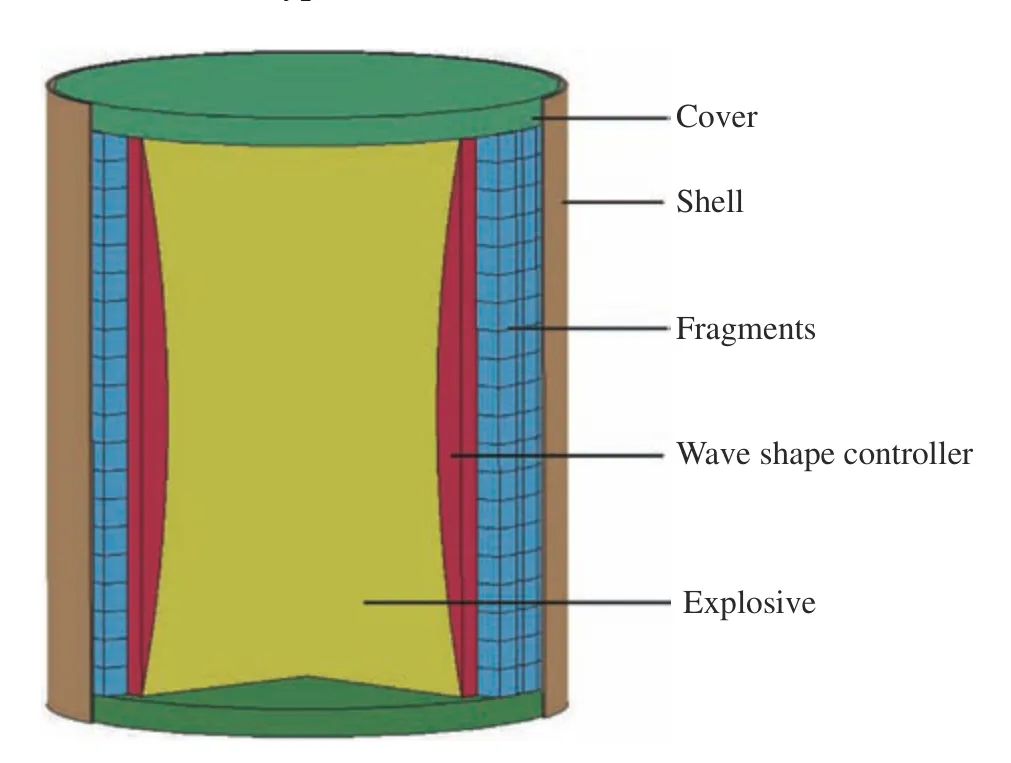
图6 杀伤战斗部数值计算模型Fig.6 Numerical calculation model of fragmentation warhead

2.2 材料参数

主装药为HMX 炸药，采用高能炸药燃烧材料模型HIGH_EXPLOSIVE_BURN 和JWL 状态方程来描述主装药的爆轰过程。JWL 状态方程可精确描述炸药在爆轰驱动过程中气体产物压力随体积和初始能量的变化关系，JWL 状态方程为：

根据表1 中的数值计算模型参数建立了4 种杀伤战斗部数值计算模型，其中不含波形控制器的模型记为A1，含波形控制器且波形控制器材料为尼龙、聚氨酯、聚四氟乙烯（polytetrafluoroethylene，PTFE）的模型分别记为A2、A3、A4。除波形控制器参数不同外，4 种模型的其余部分结构与材料参数都相同。

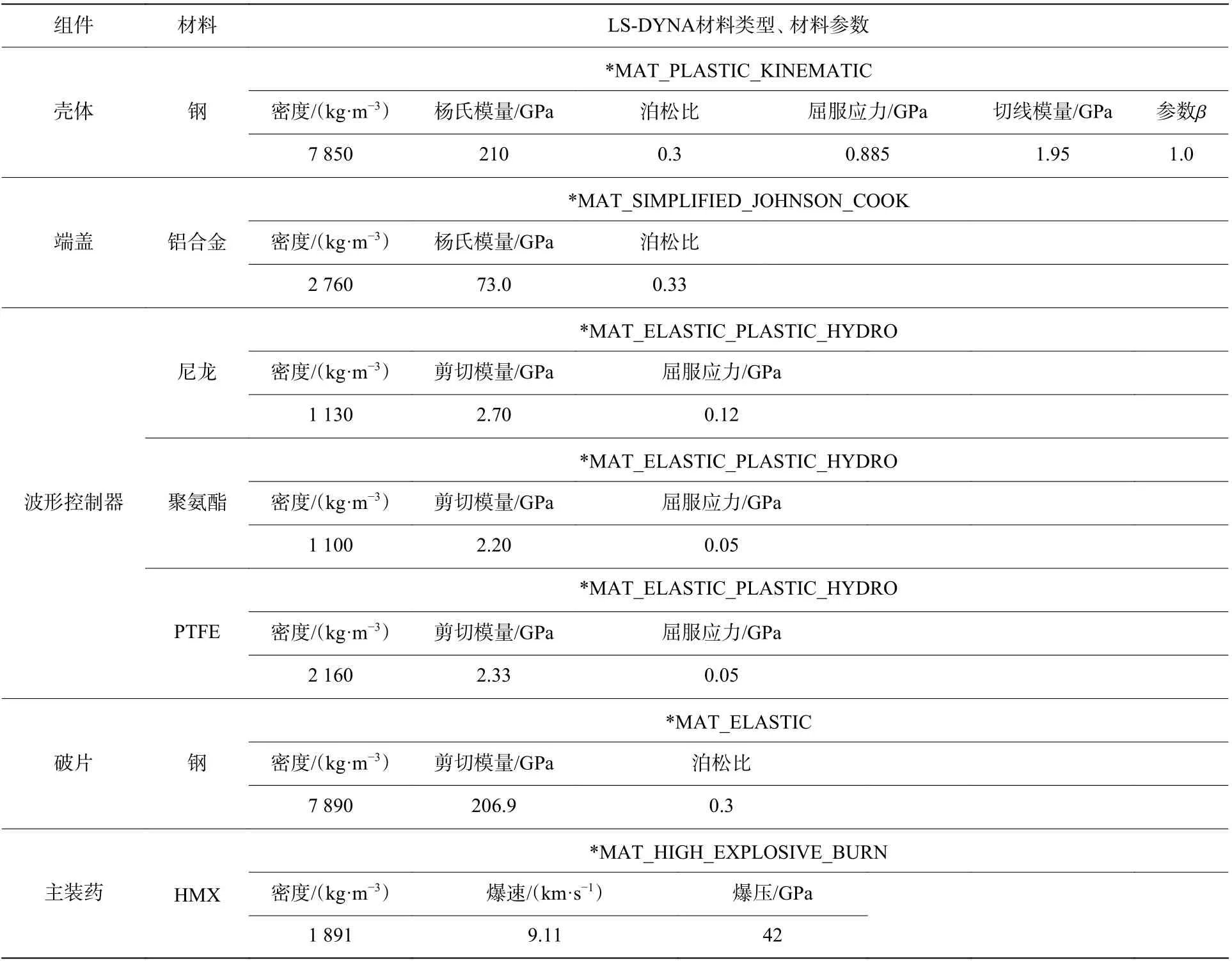
表1 数值计算模型参数[15-16]Table 1 Parameters of numerical calculation model[15-16]

2.3 数值计算结果分析

对模型A1、A2、A3、A4的破片飞散过程进行数值计算，计算时长300 µs，起爆方式都采用中心点起爆。其中模型A1破片的飞散过程如图7 所示，模型A2的破片飞散过程如图8 所示。

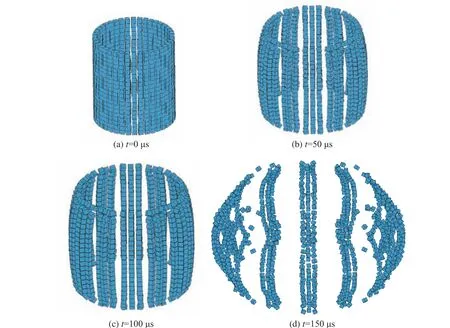
图7 战斗部数值模型A1 的破片飞散过程Fig.7 Fragments scattering process of warhead numerical model A1

图8 战斗部数值模型A2 的破片飞散过程Fig.8 Fragment scattering process of warhead numerical model A2

2.3.1 破片飞散速度

对破片正视图最前列的20 枚破片按1～20 的顺序从下至上依次编号。根据数值计算结果，得到模型A1和A2中编号1～20 的破片速度与破片编号变化关系分别在t=20，30，50，100 µs 时的图像，如图9所示。

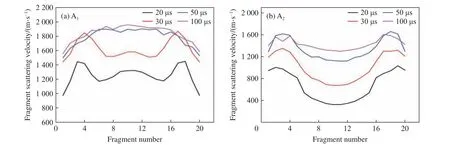
图9 战斗部数值模型破片速度与破片的关系Fig.9 Relationship between fragment scattering velocity and fragment number of warhead numerical model

由破片飞散过程图可以看出，不含波形控制器的模型A1与含波形控制器的模型A2的破片空间分布和破片速度差异较大：对于A1，刚起爆时两端和中心位置破片速度较小，之后中心位置的破片速度不断增大，在约50 µs 后，破片速度呈现出中间大两端小的分布；而对于A2，刚起爆时中心位置破片速度较小，两端破片速度较大，之后中心位置的破片速度不断增大，在约50 µs 后，所有位置破片速度几乎相同。因此波形控制器减小了不同位置破片稳定后的飞散速度差异，改善了破片飞散速度的一致性。

模型A1～A4的破片速度随时间的变化关系如图10 所示，其中正视图最前列20 枚破片飞散速度的平均值如表2 所示。

表2 破片飞散速度数值计算结果Table 2 Numeral calculation results of fragment scattering velocity

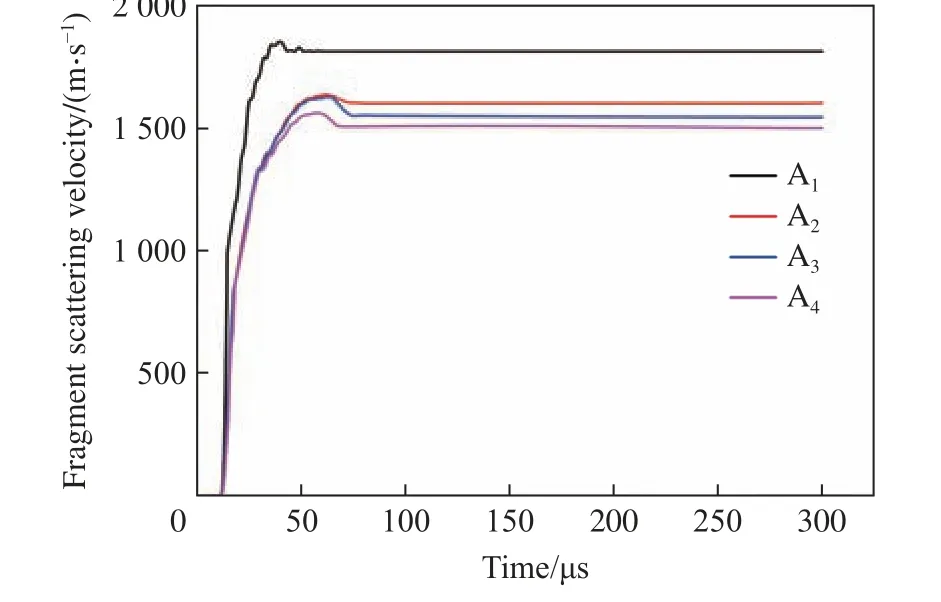
图10 破片飞散速度与时间的关系Fig.10 Relationship between fragment scattering velocity and time

由图10 和表2 可知：波形控制器降低了破片飞散速度，与无波形控制器的杀伤战斗部数值计算模型相比，含波形控制器材料为尼龙、聚氨酯和PTFE 的战斗部数值计算模型破片飞散速度分别降低了11.66%、14.57%和16.72%。

2.3.2 破片飞散角

对模型A1～A4的破片空间分布进行统计分析和计算，得到破片飞散角结果。为研究波形控制器对战斗部不同位置破片的飞散方向角的影响，统计了模型A1和A2中某一列破片的飞散方向角与破片编号的关系，如图11 所示。统计所有列破片的飞散方向角，计算得到破片飞散角，破片飞散角与战斗部计算模型编号的关系如图12 所示。

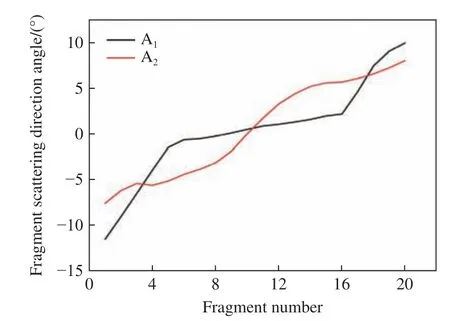
图11 破片飞散方向角与破片的关系Fig.11 Relationship between fragment scattering direction angle and fragment number

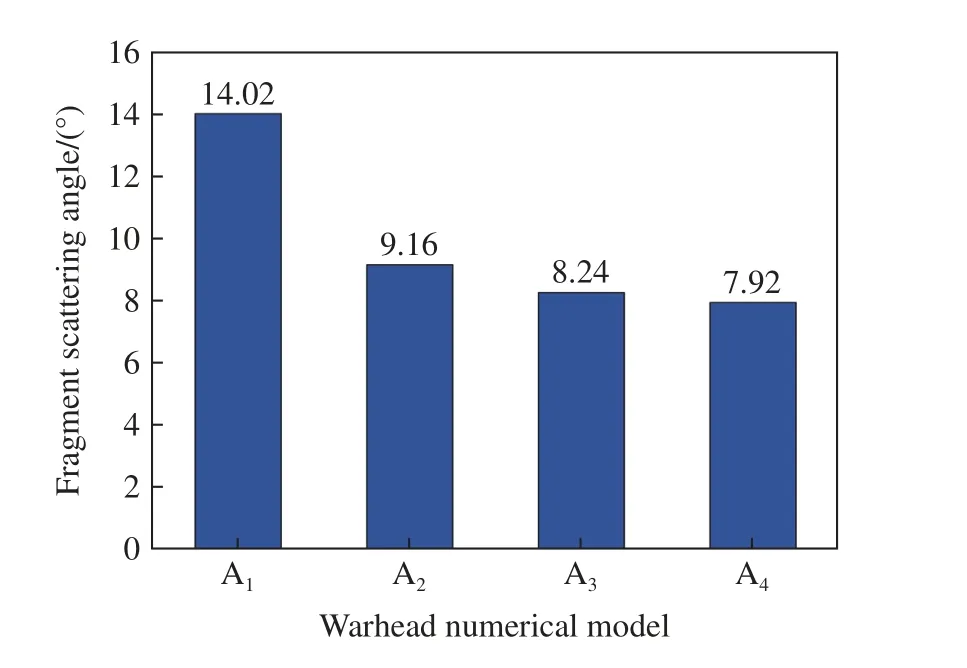
图12 数值计算破片飞散角柱状图Fig.12 Histogram obtained from numeral calculation of fragment scattering angle

由以上分析可以得到如下结论：通过数值计算分析，波形控制器可以有效地控制破片飞散方向，所设计的波形控制器减小了战斗部数值计算模型的破片飞散角；不含波形控制器的战斗部破片轴向空间分布在中心位置密度大，两端密度小，而含波形控制器的战斗部破片在轴向分布更均匀；与无波形控制器的杀伤战斗部数值计算模型相比，含波形控制器材料为尼龙、聚氨酯和PTFE 的战斗部数值计算模型破片破片飞散角分别减小了34.66%、41.22%和43.51%。

3 试验验证

为了验证波形控制器控制破片飞散特性的合理性和战斗部数值计算结果的准确性，设计了相同参数的杀伤战斗部原理样机，进行地面静爆试验来获得破片飞散特性参数。

3.1 试验设计

设计了4 发战斗部原理样机，战斗部原理样机照片如图13 所示，长度为200 mm、外径160 mm，由钛合金壳体、800 枚全预制钢破片、主装药、波形控制器及前后端盖等组成。中心起爆预留的圆筒设计为两端对称且直径很小的形状，对战斗部破片飞散角几乎无影响；预留圆筒使装药量减少，会使破片飞散速度降低，但影响很小。

图13 杀伤战斗部原理样机照片Fig.13 Photo of a prototype of the fragmentation warhead

战斗部原理样机地面静爆试验靶场布局由战斗部、弹架、钢靶板、高速摄影相机、测速系统等组成，如图14 所示。主靶板采用弧长10 m、半径10 m、高3 m、厚10 mm 的Q235A 钢板，副靶板采用弧长7.5 m、半径6 m、高2 m、厚6 mm 的Q235A 钢板，两块靶板上分别分布有4 路测速靶。

图14 靶场布局示意图Fig.14 Schematic diagram of the layout of the shooting range

3.2 试验结果

3.2.1 破片飞散速度

采用通断靶法测量破片飞散速度，其中A2战斗部原理样机的高速摄影照片如图15 所示。

图15 静爆试验高速摄影照片（战斗部A2）Fig.15 High-speed photography of static explosion test (warhead A2)

由静爆试验得到的A1～A4战斗部原理样机的破片飞散速度与数值计算得到的破片飞散速度对比如表3 所示，破片飞散速度试验值与战斗部编号的关系如图16 所示。

表3 静爆试验与数值计算破片飞散速度对比Table 3 Comparison of fragment scattering velocity values between static explosion test and numerical calculation

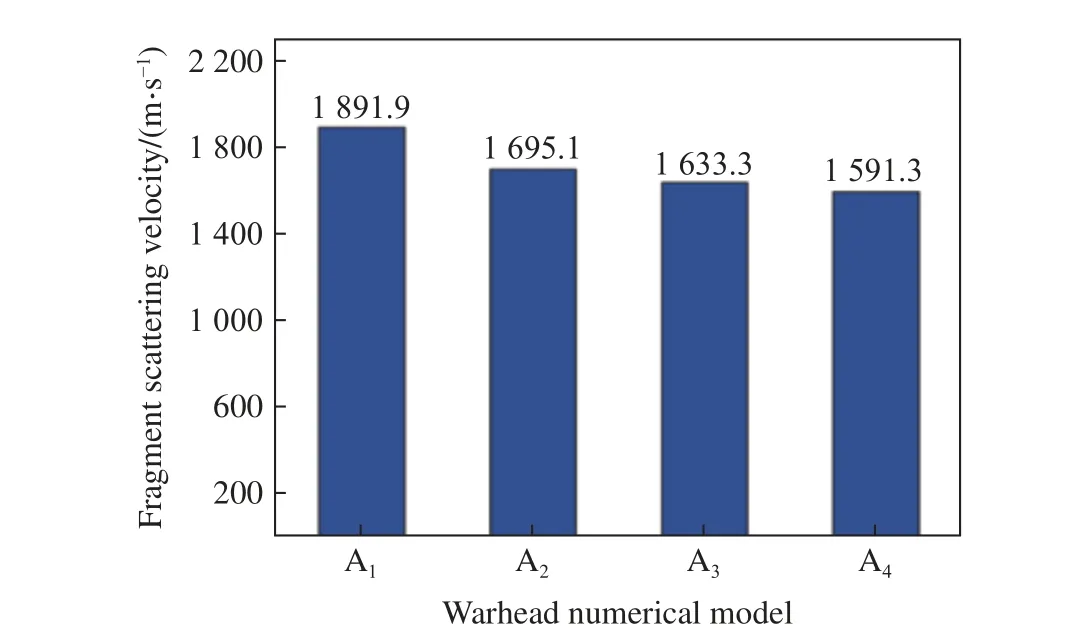
图16 静爆试验破片飞散速度柱状图Fig.16 Histogram of fragment scattering velocity in static explosion test

由上述分析可以得到以下结论：战斗部破片速度的数值计算值与试验值误差在5.47%之内，在含有波形控制器的战斗部原理样机中，波形控制器材料为尼龙时破片飞散速度最大，为聚氨酯时破片飞散速度次之，为PTFE 时破片飞散速度最小；与无波形控制器相比，含波形控制器的杀伤战斗部原理样机破片飞散速度均有所降低，波形控制器材料为尼龙、聚氨酯和PTFE 的破片飞散速度分别降低了10.40%、13.67%和15.89%。

3.2.2 破片飞散角

统计了战斗部原理样机A1～A4的破片在威力半径10 m 处钢靶板上的破片分布情况，其中A2破片在靶板上的分布如图17 所示，根据破片在靶板上的分布情况，统计出破片的轴向分布情况，如图18 所示，计算得到战斗部原理样机的破片飞散角结果，如表4 所示。

表4 静爆试验与数值计算破片飞散角值对比Table 4 Comparison of fragment scattering angle values between static explosion test and numerical calculation

图17 威力半径10 m 处破片分布图（战斗部A2）Fig.17 Distribution map of fragments with a power radius of 10 m (warhead A2)

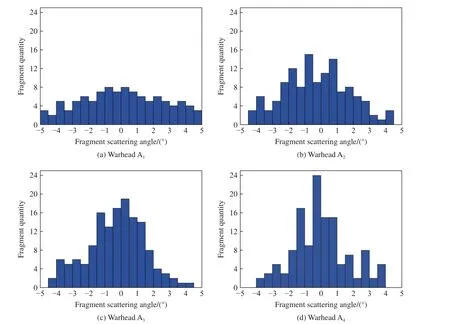
图18 破片轴向分布柱状图Fig.18 Histogram of fragment axial distribution

由上述分析可以得到如下结论：根据战斗部原理样机静爆试验结果，所设计的波形控制器减小了战斗部原理样机的破片飞散角，破片飞散角数值计算值与试验计算值误差在6.53%之内；与无波形控制器的杀伤战斗部原理样机相比，含波形控制器且材料为尼龙、聚氨酯和PTFE 的战斗部原理样机破片破片飞散角分别减小了40.00%、44.00%和46.67%。

4 结 论

提出通过在主装药与破片之间增加波形控制器的方法改善杀伤战斗部破片飞散特性，并通过数值计算和试验验证了该方法的合理性，并得到以下结论。

(1) 验证了提出的波形控制器曲线设计方法的合理性，波形控制器材料为尼龙时，战斗部飞散角数值计算值与理论设计值误差为8.40%，战斗部飞散角试验值与理论设计值的误差为10.00%。

(2) 波形控制器可以减小杀伤战斗部破片飞散速度差异，使破片在轴向的空间分布更均匀，改善了破片轴向飞散一致性。

(3) 与无波形控制器相比，波形控制器材料分别为尼龙、聚氨酯和PTFE 时，杀伤战斗部破片速度数值计算值分别减小了11.66%、14.57%和16.72%，破片速度试验测量值分别减小了10.40%、13.67%和15.89%，不同材料波形控制器的破片速度由大到小依次为：尼龙、聚氨酯、PTFE。

(4) 与无波形控制器相比，波形控制器材料分别为尼龙、聚氨酯和PTFE 时，杀伤战斗部破片飞散角数值计算值分别减小了34.66%、41.22% 和43.51%，破片飞散角试验计算值分别减小了40.00%、44.00%和46.67%，不同材料波形控制器的破片速度由大到小依次为：尼龙、聚氨酯、PTFE，波形控制器可以有效减小破片飞散角，增加破片分布密度。