液压膨胀环恒应变率加载技术*

李嘉皓，徐 便，郑宇轩,2，周风华

（1.宁波大学冲击与安全工程教育部重点实验室，浙江 宁波 315211；2.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999）

研究金属的冲击拉伸碎裂问题通常采用膨胀环（壳）实验，目前膨胀环实验技术主要为由Johnson 等[1]提出的爆炸膨胀环技术和由Niordson[2]提出的电磁膨胀环技术。但在早期的实验技术中，金属圆环的膨胀过程较为复杂，定量分析圆环的力学性能通常较困难。自20 世纪80 年代，学者们对其做了大量改进，解决了技术和测量上的诸多问题[3-6]。中国工程物理研究院流体物理研究所对电磁膨胀环和爆炸膨胀环技术均开展过相关实验研究，桂毓林等[7-8]改进了快速放电和短路开关，在不采用雷管开关的情况下实现了试件的自由膨胀，利用改进的电磁膨胀环技术研究了无氧铜的动态断裂与破碎特征；汤铁钢等[9-10]建立了爆炸丝线起爆方式的爆炸膨胀环实验技术，能较好地实现爆炸膨胀环实验的均匀起爆和金属圆环的自由膨胀。目前，大多数学者都致力于自由膨胀实验技术的优化和改进，主要原因是研究材料本构关系时，圆环在自由膨胀过程中径向分量上外力为零，从而可以简便地获取材料在环向均匀拉伸作用下的一维应力-应变关系，但圆环自由膨胀的同时也会导致试件在膨胀断裂过程中的拉伸应变率逐渐降低，初始加载与断裂时刻的应变率甚至会存在量级上的差别，这给研究应变率敏感材料的拉伸碎裂问题带来了极大的不便。

针对准一维冲击拉伸碎裂问题，Mott[11]提出了卸载波传播距离控制碎片平均尺寸的思想，Grady[12]和Kipp 等[13]进一步完善了Mott 卸载波理论，通过引入一个与断裂能量相关的内聚断裂模型来描述理想刚塑性材料的冲击拉伸碎裂过程，并获得了碎裂产生碎片的平均尺寸L=[24Gc/(ρε˙2)]1/3，其中L为碎片的平均尺寸，Gc为材料的断裂能，ρ 为材料的密度，ε˙ 为断裂时刻的应变率。显然，碎片的平均尺寸强烈依赖于加载应变率，而加载过程中应变率跨度极大的自由膨胀给分析带来了极大的难度。在冲击拉伸碎裂研究过程中，重点关注的是加载应变率和碎片平均尺寸及其分布，因而在该问题下的膨胀环实验技术可以忽略非自由膨胀带来的复杂应力分析，而应该尽可能地实现恒定应变率加载。

郑宇轩等[14]、张佳等[15]发展了一种基于Hopkinson 压杆的液压膨胀环实验技术，利用液体体积近似不可压缩的特性，通过液压腔截面积的大比例缩小，实现较低速度的活塞冲击转化为圆环试件沿径向的高速膨胀，促使圆环产生拉伸碎裂。在该实验装置的基础上，本文中，拟通过合理控制液体的加载速度和加载时长，实现金属圆环的近似恒定应变率加载。从理论上给出实现金属圆环恒应变率膨胀所需液压加载曲线的近似表达式，通过流固耦合的有限元数值分析方法的优化和改进，反推能实现圆环恒定环向应变率加载的水流速度时程曲线，并在分离式霍普金森压杆（split Hopkinson pressure bar, SHPB）上通过波形整形器来获得期望的加载入射波形，通过加入活塞限位器来控制液体的加载量，从实验上获得与理论水流加载速度相近的加载方式，利用激光干涉测速仪（displacement interferometer system for any reflector，DISAR）测量金属圆环膨胀过程中外表面的粒子径向速度，从而获得应变率时程曲线，验证该恒应变率加载技术的可行性。

1 理论分析

在前期工作中，液压膨胀环实验技术能有效地实现固体的冲击拉伸碎裂[15-17]，如图1 所示。前期的实验装置采用凸台结构，加载过程中液体持续加载时间较短，从而实现近似的自由膨胀。但如果要实现恒定应变率加载，液体必须持续作用于膨胀环，由于金属圆环直径在膨胀过程中逐渐增大，因而加载速度也必须单调递增。

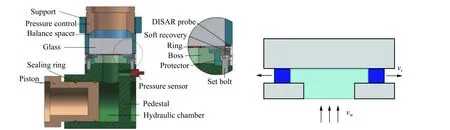
图1 液压膨胀环装置原理示意图[15]Fig.1 Schematic diagram of the liquid-driving expanding ring[15]

实验中采用的加载液体为水，假设其为近似不可压缩的无黏液体，因此在膨胀环发生断裂前，单位时间内水流加载的流量近似等于膨胀环内腔增加的体积，即：

式中：R为加载水流流道的半径，为不变量；vw为液体的加载速度；vr为环的径向膨胀速度；h为膨胀环的高度，在颈缩前变化不明显，因而假定近似不变；r为膨胀环当前时刻的半径，表达式为：

式中：r0为膨胀环的初始半径，ε 为环的环向应变。

膨胀环在膨胀过程中的应变率为：

将式(1)～(3)联立，简化可得：

式(4)即为整个膨胀过程的水流加载方程。如图2 所示，考虑实验过程中不可能为突加载荷，因而假定膨胀环在膨胀过程中的应变率分为线性增长阶段和应变率稳定阶段。线性增长阶段的加载时间为t1，相对应的加载水流速度为vw1，此时膨胀环产生的应变为ε1；应变率稳定阶段的应变率为 ε˙1，相对应的加载水流速度为vw2。

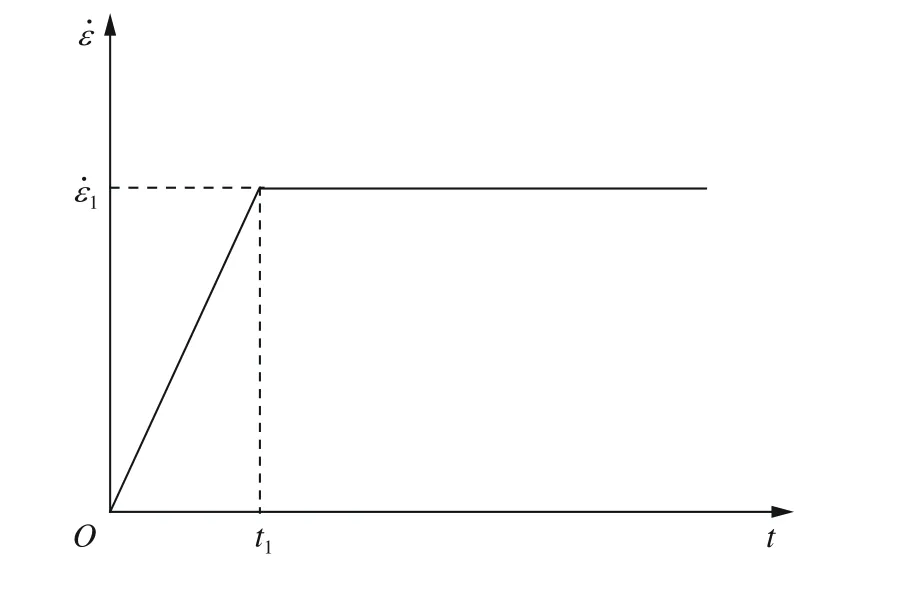
图2 理想恒应变率膨胀时程曲线Fig.2 Time history curve of strain-rate in ideal expansion

对于应变率线性增长阶段的水流加载方程，有：

式(9)给出了获得恒应变率加载的近似水流加载曲线，该曲线为双线性表达式，在数值模拟和实验中均能较好地实现。

2 有限元模拟

2.1 有限元模型

利用Abaqus/Explicit 显式动态分析有限元软件对膨胀环在液压高速驱动下的拉伸碎裂过程进行流固耦合数值模拟，采用Abaqus/CEL（coulpled Euler Lagrange）模拟水流冲击过程[18]。数值模拟采用实验使用的膨胀环试件几何模型：内径32 mm、外径35 mm，横截面为1.5 mm×1.5 mm的正方形；以水作为驱动液体，简化实际实验装置，建立相对应的液压冲击膨胀环的几何模型，如图3 所示。

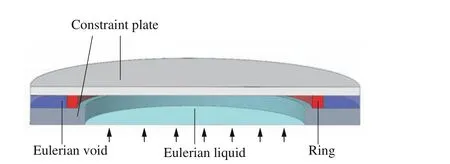
图3 液压膨胀环的有限元模型Fig.3 Finite element model of liquid-driving expanding ring

水的材料模型采用Us-Up状态方程，密度为1 000 kg/m3，黏性系数为0.001 Pa·s。膨胀环试件采用的材料为1060-O 纯铝，材料模型采用Johnson-Cook 热黏塑性本构模型描述其动态变形及热软化特性，采用线性内聚力断裂Johnson-Cook 损伤断裂模型描述其碎裂过程，具体材料参数来自文献[19]，如表1 所示。表中：ρ 为密度，c为比热容，β 为Taylor-Quinney 系数，θt为环境温度，θm为熔点温度，E为杨氏模量，µ为泊松比，A、B、C、n和m为 Johnson-Cook 模型参数，ε˙0为参考应变率，d1～d5为失效参数。欧拉域的单元类型为EC3D8R，网格平均尺寸0.3 mm，总网格数为340 000；膨胀环试件单元类型为C3D10M，网格平均尺寸0.18 mm，总网格数为260 000。

表1 1060-O Al 的材料参数[19]Table 1 Parameters of 1060-O aluminum[19]

2.2 计算结果

选取线性上升阶段的加载时间t1=40 µs，设定稳定阶段的应变率 ε˙1为4 000、6 000、8 000 和10 000 s-1，数值模拟中的几何模型参数与实验条件一致，如表2 所示。根据式(9)，可以获得不同恒定应变率下的水流加载曲线，如图4 所示。

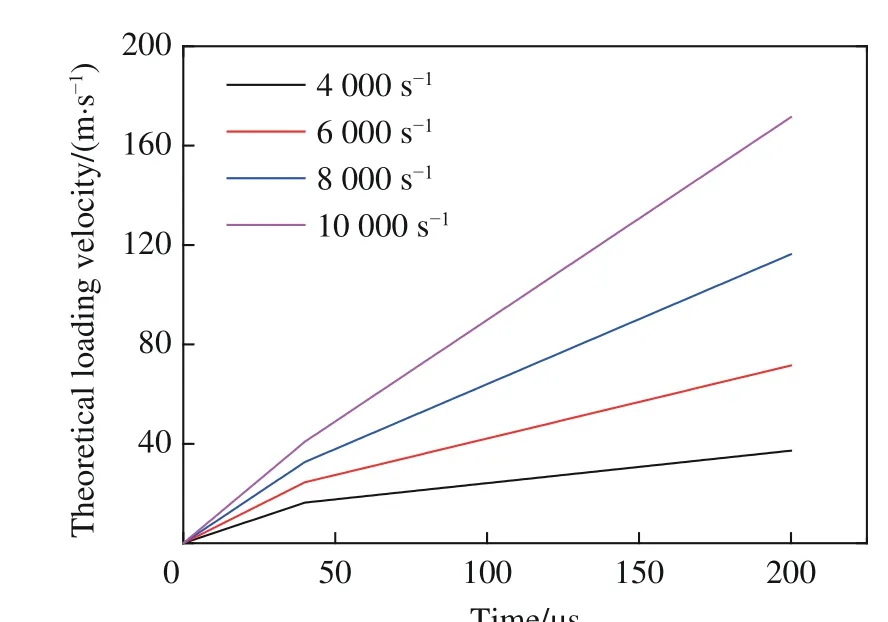
图4 理论计算所得的水流加载曲线Fig.4 Time history curves of theoretical loading velocities at different strain rates

表2 加载曲线中的基本物理参数Table 2 Physical parameters in the loading curve

图5 给出了不同加载条件下的1060 铝环膨胀过程中径向粒子速度的时程曲线。由于水流加载端的载荷传递到膨胀环内壁需要一定时间，因而膨胀环的径向粒子速度起始点较加载波形略晚5～10 µs，相应的应变率线性增长阶段也略晚，在约48 µs 结束。在应变率线性上升阶段加载结束时，施加在膨胀环内壁的水流由于惯性效应将导致径向粒子速度过冲，而应变率稳定阶段的水流加速度突降，从而使得应变率稳定阶段初期膨胀环的径向粒子速度并没有立即升高，而是保持平稳甚至下降，而后径向粒子速度再持续升高直至膨胀环断裂。

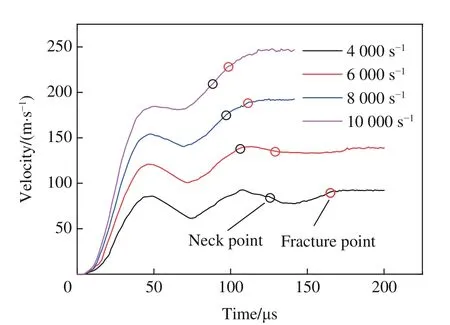
图5 径向膨胀速度曲线Fig.5 Expanding velocity under hydraulic loading

不同加载条件下1060 铝环的膨胀过程可以近似认为是恒定应变率膨胀，如图6 所示。其中，当理论应变率为4 000 s-1时，数值模拟中线性增长阶段的最终应变率略大于理论值；当理论应变率为6 000 s-1时，数值模拟中线性增长阶段的最终应变率与理论值相当；当理论应变率为8 000 和10 000 s-1时，在相同时间t1内产生的应变显著大于低应变率的情况，忽略应变率线性增长阶段的应变将产生较大偏差，因而数值模拟中线性增长阶段的最终应变率明显低于理论值。同时可以发现，径向膨胀应变率的峰值均明显大于平均应变率，造成该现象的主要原因是水流惯性效应引起的径向速度过冲。但是在加载中后期，应变率回落后，圆环的膨胀应变率基本在一个恒定值附近波动，应变率的波动范围为20%以内。同时可以发现，随着加载应变率的提高，断裂点会不断提前，应变率稳定阶段也越来越短，因而在很高的加载应变率下，该实验技术将无法实现恒定应变率加载。

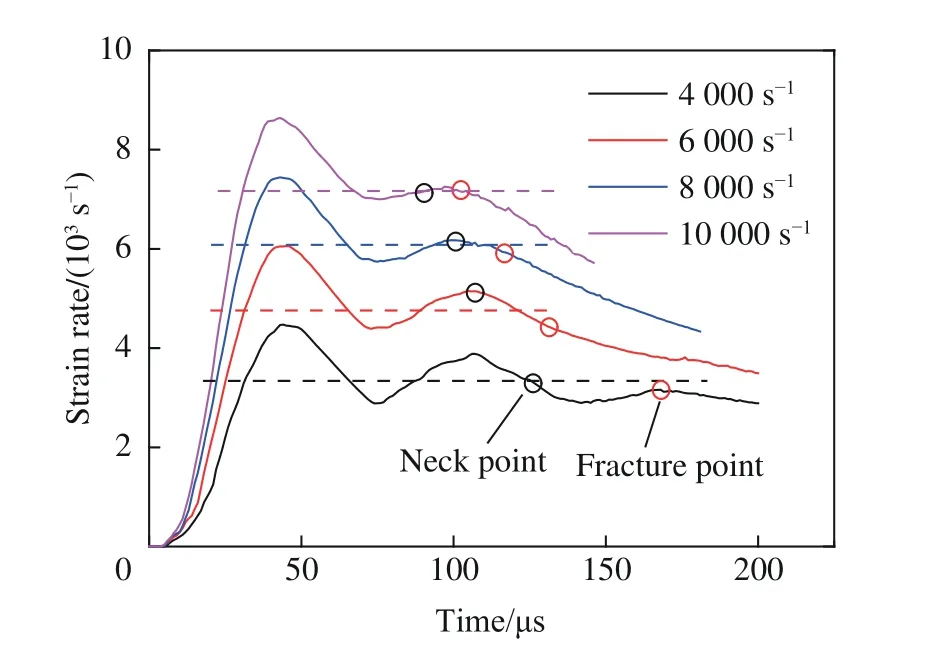
图6 膨胀环的应变率历史曲线Fig.6 Time history curves of expansion strain rates

选取稳定阶段理论应变率6 000 s-1为典型工况，系统分析冲击拉伸碎裂过程中膨胀环的力学行为和加载曲线的影响因素。首先分析圆环外侧某质点在膨胀过程中的质点速度和应力状态。图7 给出了膨胀环的环向速度和径向速度时程曲线，在膨胀环发生显著颈缩之前，膨胀环环向速度基本为零，表明膨胀环在加载过程中为均匀的拉伸加载，在环向上没有应力波扰动；而当膨胀环发生显著颈缩后，环向速度会有一个明显的速度突变，表明相邻断口发出的Mott 卸载波传播到了相应位置。

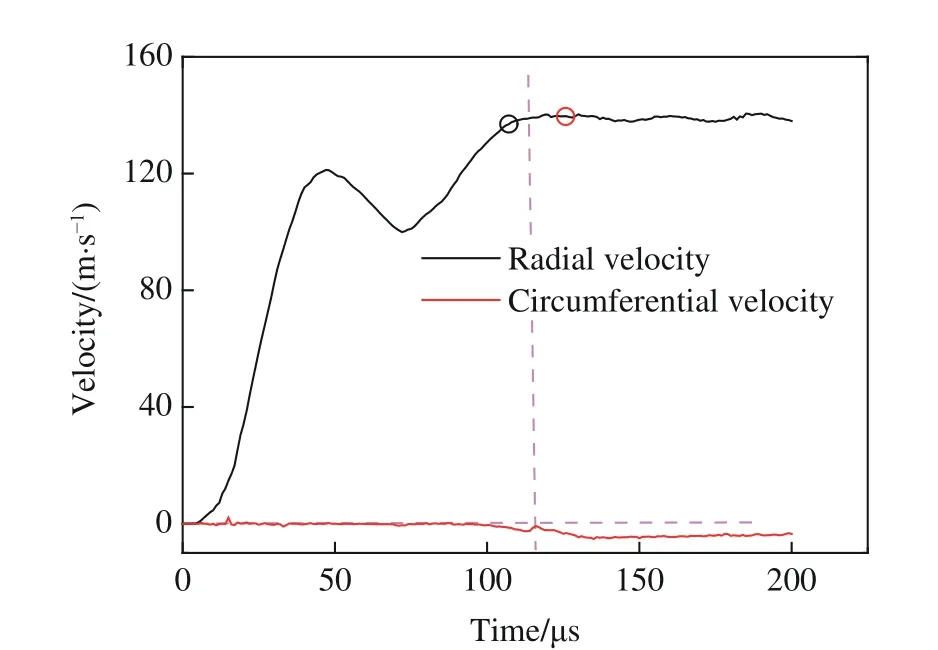
图7 膨胀环环向速度和径向速度时程曲线（应变率6 000 s-1）Fig.7 Time history curves of radial velocity and circumferential velocity at the strain rate of 6 000 s-1

图8 给出了非颈缩区外壁及内壁单元的环向应力和径向应力时程曲线。在整个膨胀过程中，外壁处的径向应力基本为零，但内壁在水流的冲击下径向应力存在较大的变化；同时，内外壁的环向应力整体接近，并且环向应力卸载阶段与图7 中环向速度突变时间相近，也可佐证此时断口发出的Mott 卸载波传播到了相应位置。

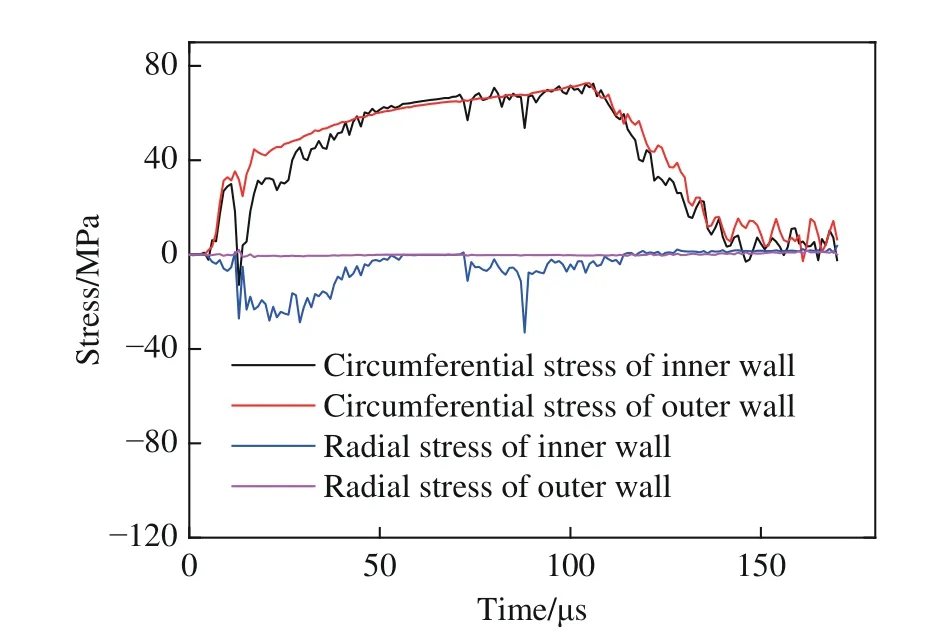
图8 膨胀环环向应力和径向应力时程曲线（应变率6 000 s-1）Fig.8 Time history curves of radial stress and circumferential stress at the strain rate of 6 000 s-1

由图6 可见，应变率增长阶段能较好地达到预定的应变率，但是稳定应变率阶段前期的应变率下降较快。因此，在理论基础上，人为调高稳定应变率阶段的加载曲线的斜率，如图9 所示。数值模拟结果表明，提高加载速率能有效地提高应变率的幅值，更好地实现恒定应变率加载，如图10 所示。

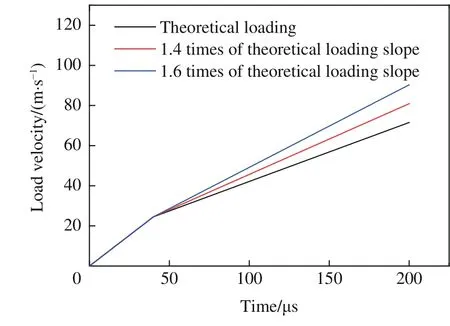
图9 改进后的水流加载曲线Fig.9 Modified curves of loading velocity

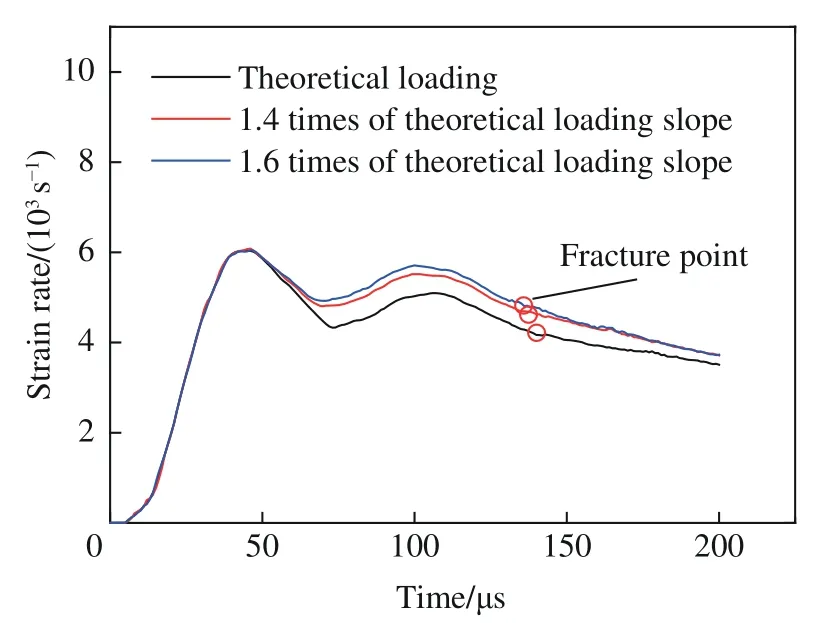
图10 改进后的应变率曲线Fig.10 Modified curves of strain rate

进一步探究应变率增长阶段的时间t1对膨胀环应变率时程曲线的影响，其水流加载曲线如图11 所示。图12 给出了断裂前应变率增长阶段不同时间t1下的应变率时程曲线。结果表明，应变率增长阶段所需的时间越短，即水流前期加载越迅速，膨胀过冲的应变率越高，并且难以实现较明显的应变率稳定。适当地增加应变率增长阶段的时间t1来抵消水流加载的惯性效应，可以有效地提高应变率的稳定性。

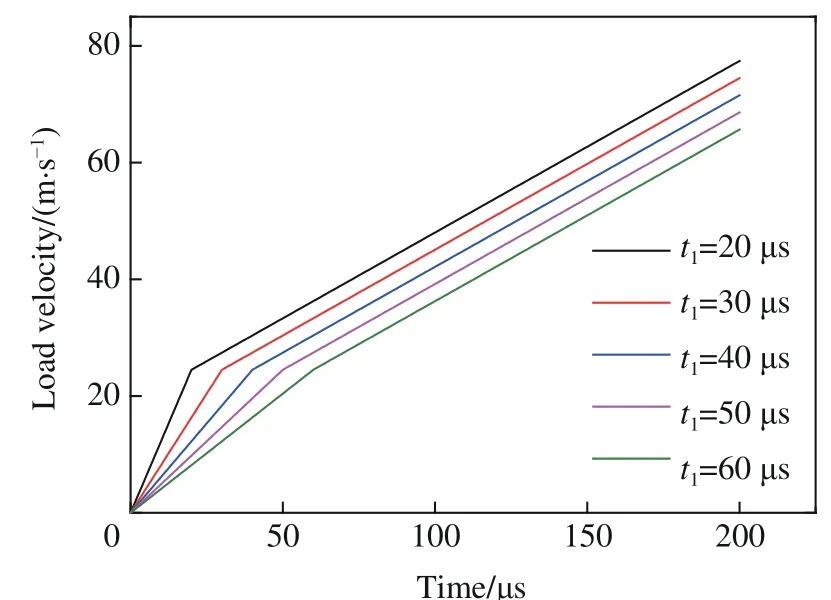
图11 不同应变率增长阶段下的水流加载曲线Fig.11 Loading curves in different strain rate growth phase

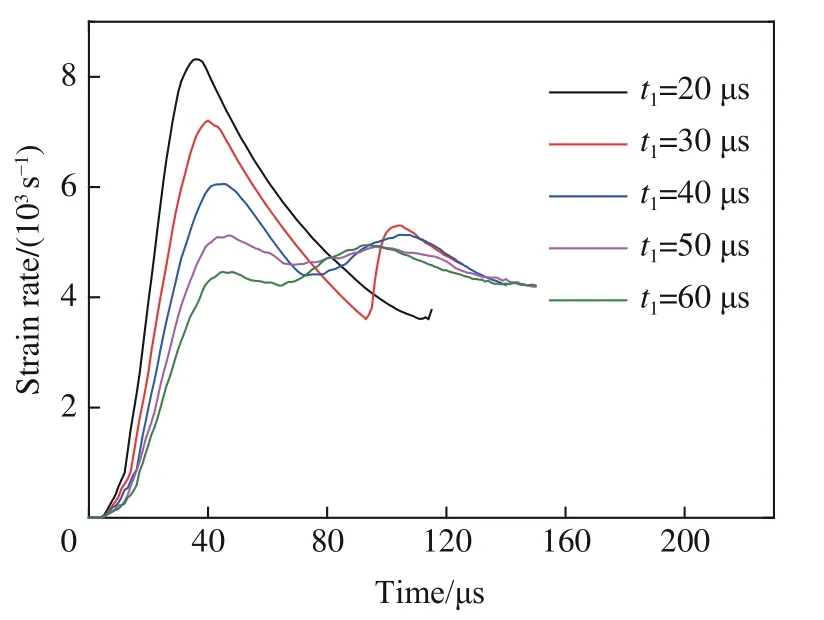
图12 不同应变率增长阶段时间下的应变率时程曲线Fig.12 Strain rate curves in different strain rate growth phase

3 实验验证

采用 ∅ 74 mm 的分离式霍普金森压杆系统，将液压膨胀环实验装置置于入射杆和透射杆之间，采用紫铜片作为整形器，撞击杆长度为400 mm，气压为0.5 MPa，活塞限位位移为0.8 mm。利用DISAR 获得膨胀环的径向粒子速度，实验中用于连接测速仪的光纤探针固定于探针支架上，探针端部正对膨胀环外表面，如图13 所示。膨胀环试件为1060-O 铝环，圆环表面经过打磨处理，尽量减小机械加工带来的初始缺陷的影响，圆环内径32 mm、外径35 mm，横截面为1.5 mm×1.5 mm 的正方形。

图13 液压膨胀环实验装置Fig.13 Experimental device of the liquid-driving expanding ring

通过入射杆上的入射波和反射波可以得到活塞的加载曲线，假定水为近似不可压缩液体，可近似获得水流加载速度曲线，如图14 所示。当线性增长阶段的速度峰值为10 m/s 时，理论上的稳定应变率约为2 450 s-1。通过DISAR 测得膨胀环表面的径向膨胀速度，对径向速度曲线进行积分，并根据式(3)即可得到膨胀环的应变率时程曲线，如图15 所示。实验结果表明，在加载的中后期，膨胀环的径向应变率稳定在约2 000 s-1，上下波动约为10%，能较好地实现恒定应变率加载；同时，由于实验中不可避免的能量损耗，实验获得的加载应变率略低于理论预测应变率。

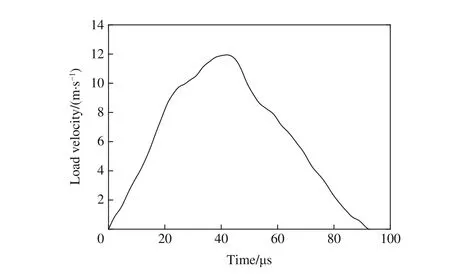
图14 实验中的水流加载速度曲线Fig.14 Loading velocity curve in experiment

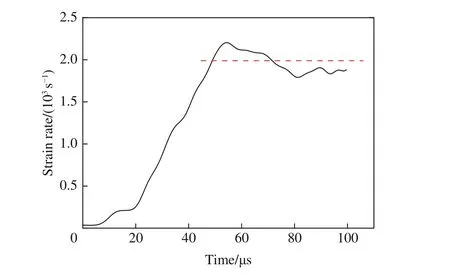
图15 实验中的应变率曲线Fig.15 Strain rate obtained in experiment

4 结 论

发展了一种能实现膨胀环近似恒定应变率膨胀的液压加载技术，利用液体体积近似不可压缩的特性，通过液压腔截面积的大比例缩小，将持续的水流轴向加载转化为膨胀环稳定的径向膨胀。假定金属圆环的膨胀应变率为线性增长阶段和稳定阶段，从理论上给出了实现恒应变率膨胀所需的水流加载曲线的近似表达式，对应曲线为双线性加载曲线。

通过流固耦合有限元模拟，再现了1060-O 铝环的液压膨胀碎裂过程，在不同的应变率下，理论给出的水流加载曲线均能近似实现膨胀环的恒定应变率加载。但在较高应变率加载时，忽略应变率线性增长阶段的应变，将产生较大偏差，模拟得到的应变率较理论值偏小，且应变率越高，误差越大。液压膨胀环实验进一步验证了恒应变率加载技术的可行性。