平面约束变胞机构构态切换能力的概率评估模型
孙本奇,杨强,2,*,孙志礼,李树军,3,马宏坤,王若男
1.东北大学 机械工程与自动化学院,沈阳 110819
2.辽宁工业大学 机械工程与自动化学院,锦州 121001
3.中国科学院 沈阳自动化研究所 机器人学国家重点实验室,沈阳 110016
1998 年第25 届ASME 机构学与机器人学双年 会上,Dai 和Jones[1]首次提出了变胞机构的概念。李端玲等[2]基于构态变换的矩阵运算,提出了变胞机构的结构综合方法。戴建生等[3]系统阐述了变胞原理,提出了变胞机构的延伸和分类。王德伦和戴建生在探究变胞机构组成和表达方式的基础上,建立了变胞机构的变胞方程[4]。Gan 等[5]设计了一种新型可重构rT 胡克铰链,并据此提出了2种并联变胞机构。Li 和Dai[6-7]提 出了扩展Assur 杆组的概念和基于扩展Assur 杆组的变胞机构组成原理,引入了变胞机构等效阻力的概念并定义了变胞副的等效阻力系数函数。张武翔等[8]提出了一种基于约束变化特征分析的变胞机构构型综合方法。杨强等[9]研究了含变胞副结构的约束变胞机构构型综合。Li 等[10]提出了变胞副约束阻力的模块化计算模型。Yang等[11]基于结构综合矩阵提出了一种平面变胞机构的通用结构设计方法。王汝贵和陈辉庆[12]针对变胞机构多失效模式的运动可靠性问题提出了一种基于变量状态空间的可靠性分析与优化设计方法。王兴东等[13]考虑关节间隙、连杆制造公差、连杆和关节热变形等多源不确定性因素建立了一种平面五杆变胞机构的全构态运动可靠性模型。
变胞机构的可折叠性使其在航空航天领域可用来部分代替可展式机构,如星球探测车、空间机械臂、卫星可展天线、太阳能帆板、太空望远镜展开机构等。Joshi 等[14]将变胞可重构性应用于飞机机翼结构并展示了可变形机翼对飞机性能的影响。张克涛等[15]将变胞机构应用于腿轮式探测车的车身设计,使探测车能够以腿式和轮式两种方式移动,极大地提高了其机动性和适应性。Ding 等[16]利用变胞思想设计了新型太空舱门的开关机构。加拿大航天部门采用变胞原理研制了一款航天飞机遥控机械臂[17]。Zhao 等[18]研发了用于多任务需求的大型可重构空间多指手的变胞并联关节单元。李波等[19]设计了一种能实现星载平板天线折叠和展开的多构态变胞可展支撑桁架,并提出了一种时序可控的多杆分步展开方式。Jia 等[20]基于螺旋理论研究了一种模块化变胞机构的构型综合方法,并通过串联该模块设计了一种大型可展开抓取机械手,可用作太空机械臂。将变胞机构的设计理念应用于机械制造中,能够最大化的实现装备工装的柔性化,使其快速的适应航空航天产品的变更。王珉等[21]在双偏心变胞源机构的基础上设计了一种具有变胞功能的自主移动制孔机,实现行走和调姿制孔两个工作阶段的变自由度切换,满足了飞机自动化装配的应用需求。樊伟等[22]设计并实现了一套新型自动化可重构工装系统,解决航空航天管路组件的装配质量及效率问题。
简易的变构态/变拓扑结构能力是变胞机构的“灵魂”所在。对于以运动副变胞为特征的约束变胞机构而言,构态切换/保持主要是通过变胞副运动状态的切换/保持来实现的[23]。因此,变胞副需要设计特殊的“开关”结构来实现运动和静止状态的切换,这种“先天”的属性决定了构态切换失败是机构完成运动功能的最薄弱环节,同时构态切换能力是约束变胞机构核心的运动性能指标。目前针对变胞机构构态变换的研究较多关注于构态切换时刻的冲击特性分析[24-25]、基于虚功原理的机构整体动力学建模[26]。而从变胞副受力分析入手,开展变胞机构的构态切换能力的定义和评估,这方面的研究并不多见。目前,已有学者指出[27]:“如何平稳地切换机构的运动模式一直是一个悬而未决的问题。”
从变胞副运动状态切换的力学调控机理出发,系统开展构态切换能力的定义和评估方法研究,进而提出了一种平面约束变胞机构构态切换能力的概率评估模型,最后以折纸变胞机构的设计计算为例验证了上述模型的可行性和有效性。
1 基于扩展Assur 杆组的约束变胞机构组成原理
1.1 约束变胞机构的组成原理
文献[6]提出了9 种扩展II 级Assur 杆组的结构形式,并据此提出了基于扩展Assur 杆组的约束变胞机构组成原理。
1.2 约束变胞机构的变胞过程
图1 是一种两自由度平面约束变胞机构,由1个1-DOF 扩展Assur 杆组(RRRP 杆组)依次连接于主动件和机架构成,其中N1、N2、N3、N4、N7为机构中对应运动副的序号,N5、N6为对应连杆质心的序号,θct为构态切换时刻主动件角位置,ω为主动件角速度;图2 是该机构的运动循环图。分析图1 和图2 可知:利用变胞副R3和P7的运动状态切换(R代表转动副,P代表移动副),该机构可以获得曲柄滑块机构和曲柄摇杆机构两种工作构态/拓扑结构,并在各自的构态下完成对应的作业任务。

图1 两自由度平面约束变胞机构Fig. 1 2-DOF planar constrained metamorphic mechanism
由图1 引申可知,n个自由度的约束变胞源机构可通过设置n个变胞副获得n个构态。由图2可知,为获得所有的工作构态,变胞副必须依次被约束(处于静止状态)。显然,变胞副的运动规律取决于作用在其上的驱动力(力矩)和约束力(力矩)。
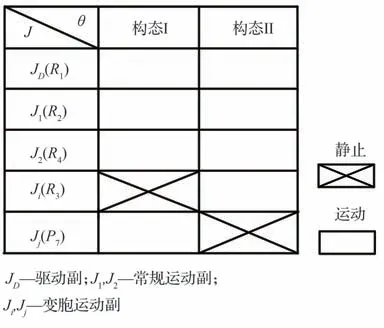
图2 两自由度平面约束变胞机构运动循环图Fig. 2 Metamorphic cyclogram of 2-DOF planar constrained metamorphic mechanism
2 约束变胞机构模块化力分析与变胞转动副结构设计
在Assur 杆组常规受力分析[28]的基础上推导含变胞副的扩展Assur 杆组受力分析计算模型。九种扩展Assur 杆组的模块化力分析方法相同,因此以图1 所示约束变胞机构中包含的RRRP 扩展Assur 杆组为例进行分析。图3 所示为RRRP杆组的变胞过程,其中转动副2 和移动副4 为变胞副,转动副1 和转动副3 为常规运动副,下面给出模块化力分析计算模型。

图3 RRRP 杆组变胞过程Fig. 3 Metamorphic process of RRRP group
2.1 含变胞副的扩展Assur 杆组模块化力分析
第I 构态RRRP 杆组退化为RRP 杆组,受力分析如图4 所示。其中N5、N6、N7点分别为连 杆N2N3、N3N4、滑块的质心;α为变胞转动副几何约束 角;dk为弹簧当前长度;Fk为弹簧力;θ为弹簧力方向与连杆N3N4夹角;d1、d2分别为弹簧在连杆N3N4、N2N3上的安装位置与N3点的距离;γ为导路与水平方向夹角;Fγ为滑块所受外力沿导路方向分量。已知分别作用在连杆N2N3、N3N4、滑块上的外力F5、F6、F7和力矩T1、T2、T3,求解各转动副所受支反力和变胞转动副所受驱动力矩与约束力矩。
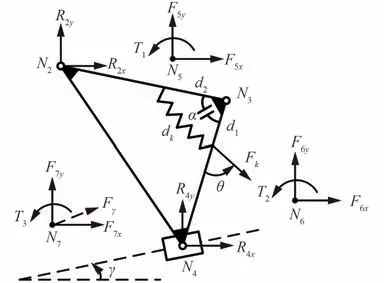
图4 RRRP 杆组退化的RRP 杆组受力分析图Fig. 4 Force diagram of RRP group degraded by RRRP group
模块化力分析步骤为
其 中:k为弹簧刚度;a为弹簧原长;Pijx、Pijy分别表示i点、j点间x、y方向的距离;Rix、Riy分别表示作用在运动副i上x、y方向的支反力;Fix、Fiy分别表示作用在i点上x、y方向的力;Tij表示i点作用力对j点力矩;Ti表示作用在i点的力矩;Tk表示弹簧力对N3点的力矩,即变胞副结构提供的约束阻力矩。
用T53、T63分别表示2 个连杆的重力对N3点的力矩,ΔT表示变胞转动副的驱动力矩,逆时针方向为正,则:
第Ⅱ构态RRRP 杆组退化为RRR 杆组,受力分析如图5 所示。其中N5、N6点分别为连杆N2N3、N3N4的质心;θ34为连杆N3N4的角位置。已知分别作用在连杆N2N3、N3N4上的外力F5、F6和力矩T1、T2,求解各转动副所受支反力和变胞转动副所受驱动力矩与约束力矩。
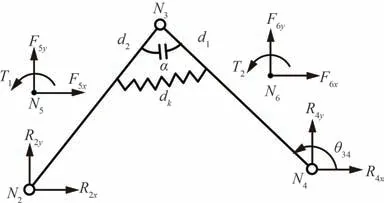
图5 RRRP 杆组退化的RRR 杆组受力分析图Fig. 5 Force diagram of RRR group degraded by RRRP group
模块化力分析步骤为
其中:Fkx、Fky分别表示弹簧力沿x、y方向的分量;变量dk、θ、Fk、变胞副约束力矩Tk、变胞副驱动力矩ΔT的计算方法和其余各变量的含义均可参照第Ⅰ构态受力分析模型。
2.2 基于模块化力分析中约束参数计算的变胞转动副结构设计
在目前变胞机构的研究中,变胞转动副往往以简图形式表示,为促进其工程应用,设计了一种简单实用的具有弹簧力约束和几何约束共同调控的变胞转动副的结构形式,如图6 所示。
如图6 所示:连杆①,端盖③和构件⑥连接后成为一个整体,连杆②和构件④通过螺栓连接后成为另一个整体。构件⑥两端的滚珠在构件④内部的凹槽内滑滚,使得两个连杆能够相对转动。销轴⑤起到几何约束的作用,构件⑥与销轴⑤接触后转动副的角度不能增大。弹簧被压缩后安装到连杆上,此时弹簧具有预紧力,当转动副的驱动力矩足够大时才能够克服预紧力即压缩弹簧开始转动。

图6 变胞转动副结构Fig. 6 Structure of metamorphic revolute joint
销轴⑤产生的几何约束提供理论上无穷大的约束力,保障角度不能增大。同时,变胞转动副要想在某个工作构态内保持静止,需满足弹簧预紧力提供的约束力矩大于整个构态内变胞副受到的最大驱动力矩,以限制角度的减小。即:
式中:Fk为弹簧预紧力;d1和θ为图4 中对应的结构尺寸。进而,可以利用式(15)计算的弹簧预紧力范围对弹簧参数进行设计。
3 基于等效阻力梯度模型的构态切换能力定义
3.1 等效阻力梯度模型
为了描述变胞副受力状况和约束特点,文献[7]建立了变胞机构的等效阻力梯度模型,旨在通过比较变胞副在运动方向上受到的驱动力(力矩)与变胞副自身结构所提供的约束力(力矩)的大小来描述变胞副的运动状态。在文献[7]中定义了一个无量纲的等效阻力系数函数:
式 中:n为构态数;θi是i构态下的驱动副位移;Fc(θi)和Tc(θi)表示变胞副在运动方向上提供的约束力和约束力矩;F(θi)和T(θi)表示变胞副在运动方向上受到的驱动力和驱动力矩。
根据最小阻力原则,变胞副的动作顺序和等效阻力系数紧密相关,要使静止变胞副的等效阻力系数大于相对运动变胞副的等效阻力系数,整个约束变胞过程的等效阻力梯度变化规律为
式中:fes(θi)为变胞副处于相对静止状态下的等效阻力系数;fem(θi)为变胞副处于相对运动状态下的等效阻力系数。
3.2 约束变胞机构构态切换能力定义
以图1 所示约束变胞机构为例,其包含的RRRP 杆组受力分析方法可参照2.1 节。根据文献[7],其变胞副R3和P7的等效阻力系数在两构态切换和保持过程中需满足以下条件:
第Ⅰ构态中变胞转动副R3始终静止且变胞移动副P7始终运动即可保证不出现运动时序错乱,并主要由变胞转动副R3决定。变胞转动副R3由式(11)中ΔT提供驱动力矩,弹簧预紧力和几何约束共同作用提供约束力矩。当ΔT<0 时,变胞转动副R3有角度增大的趋势,由于几何约束的限制,其角度保持不变。当ΔT>0 时,变胞转动副R3有角度减小的趋势并压缩弹簧,要使得变胞转动副R3保持静止,需保证弹簧提供的约束力矩始终大于驱动力矩。即:
将第II 构态初始时刻视为构态切换时刻,这一时刻变胞移动副P7开始受几何约束由运动变为静止,变胞转动副R3由静止状态变为运动状态。由于几何约束力可视为无穷大,显然变胞移动副完成运动状态切换的可靠度为1。变胞转动副R3准确地完成运动状态切换需保证这一时刻其驱动力矩ΔT大于弹簧的约束力矩。即:
第Ⅱ构态中变胞移动副P7始终静止且变胞转动副R3始终运动即可保证不出现运动时序错乱,并主要由变胞移动副P7决定。由于滑块受几何约束,约束力理论上为无穷大,滑块不会向右运动。同时还要保证滑块不会有向左的运动趋势,需要满足滑块所受的支反力沿导路的分量始终方向向右且大于外载荷沿导路的分量。即:
图7 为图1 所示机构中变胞副R3和P7的等效阻力系数f3和f7变化的理想状态,其中θ为主动件角位置,fe为等效阻力系数。

图7 两自由度约束变胞机构理想等效阻力系数Fig. 7 Ideal equivalent resistance coefficients of 2-DOF constrained metamorphic mechanism
由等效阻力梯度模型[7]可知:任意时刻等效阻力系数确定,则变胞副的运动状态确定。在构态切换时刻θct,变胞副R3由静止变为运动,变胞副P7由运动变为静止。等效阻力系数f3和f7调控变胞副R3和P7的运动状态切换,实现变胞机构从构态Ⅰ切换至构态Ⅱ。在构态切换时刻,等效阻力系数按理想设计值变化的准确性决定了约束变胞机构的构态切换能力。
4 约束变胞机构构态切换能力的概率评估模型
4.1 构态切换的随机性分析
工程实际中,由于误差随机性的影响导致按同一图纸生产的变胞机构中任意变胞副的驱动力和约束阻力不是确定值,而是具有一定分布规律的随机变量。即对于实际的约束变胞机构而言,变胞副的等效阻力系数亦为随机变量。显然,相比确定性模型,如何定义和求解构态切换成功的概率指标更具有实际工程意义。
4.2 构态切换能力的概率评估模型
已知某变胞副k的驱动力F和约束阻力Fc的随机性,当构态切换时刻该变胞副由静止变为运动时,其运动状态切换成功的可靠度为
当构态切换时刻该变胞副由运动变为静止时,其运动状态切换成功的可靠度为
式中:fs(xs)和f1(x1)分别为驱动力随机变量和约束阻力随机变量的概率密度函数。
约束变胞机构的构态切换主要通过变胞副运动状态的切换来实现的。因此,单次构态切换成功的概率(可靠度)可以定义为参与构态切换的n个变胞副运动状态切换成功的概率连乘积。即:
式中:θct为构态切换时刻主动件位置角。
由于RRRP 杆组中可以同时包含变胞转动副和变胞移动副,因此,以图1 所示包含RRRP 扩展Assur 杆组的约束变胞机构为例建立构态切换可靠度计算模型,同时为分析包含其他扩展Assur 杆组的约束变胞机构构态切换可靠性提供参考。其中,RRRP 扩展Assur 杆组受力分析方法可参照2.1 节。模型中考虑的输入误差有:构件几何尺寸误差、构件质量误差、输入角速度误差、主动件转角误差、变胞转动副几何约束角度误差、弹簧刚度误差和弹簧安装位置误差,假设上述误差随机变量相互独立且均符合正态分布。
如3.2 节所述,第I 构态机构是否产生运动时序错乱主要由变胞转动副R3是否能保持始终静止状态决定。
将式(7)、式(8)、式(10)分别代入式(11),得出变胞转动副R3的驱动力矩计算式:
将式(3)、式(5)分别代入式(6),得出变胞转动副R3的约束力矩计算式:
因此,第Ⅰ构态中变胞转动副R3运动状态保持能力的极限状态函数可表示为
构态切换时刻需满足变胞转动副R3的运动状态由静止变为运动,同时变胞移动副P7的运动状态由运动变为静止。构态切换时刻,P7受几何约束其运动状态切换的可靠度为1,因此只需判断R3是否能够准确地切换运动状态即可判断变胞机构是否能够成功完成构态切换。
将式(10)、式(12)和式(13)分别代入式(11)得出构态切换时刻变胞转动副R3的驱动力矩计算式:
构态切换时刻弹簧未被压缩,此时变胞转动副R3的约束力矩的计算式与式(25)相同。同理,构态切换时刻变胞转动副R3运动状态切换能力的极限状态函数可表示为
第Ⅱ构态机构是否产生运动时序错乱主要由变胞移动副P7是否保持始终静止状态决定。变胞移动副P7保持静止需满足滑块所受驱动力,即支反力与外力沿导路的合力始终方向向右。
滑块所受支反力沿导路方向分量的计算式展开为
滑块所受外力沿导路方向的分量Fγ如式(9)所示。多数情况下滑块所受支反力方向向右且外力方向向左,因此第II 构态中变胞移动副P7运动状态保持能力的极限状态函数可表示为
利用一次二阶矩法,可以将上述3 个运动阶段的极限状态函数表达式一阶泰勒展开,建立极限状态函数的误差模型。以构态切换时刻为例,其均值和方差分别为
由于变胞机构3 个运动阶段的极限状态函数已知,且各阶段驱动力矩和约束力矩均满足正态分布,基于应力强度干涉模型[29]各阶段机构构态切换/保持能力的运动功能可靠度为
f(Z)为极限状态函数,对应构态I,构态切换时刻和构态II,其具体表达式为式(26)、式(28)和式(30)。以构态切换时刻为例,极限状态函数Zct的具体表达式f(Zct)可由式(25)、式(27)和式(28)解得。易知各个输入参数xi的偏导数∂f∂xi容易求得,即μZ、σZ可知。限于篇幅,此处不再赘述。
如图7 所示变胞机构的等效阻力梯度曲线,在变胞机构构态切换的相邻时刻,等效阻力系数接近1,此时其值的波动更容易造成运动时序错乱。因此,在第I 构态和第II 构态内分别取a和b个等效阻力系数接近1 的构态切换相邻时刻,分别计算对应时刻的可靠度。参照串联系统的可靠度计算方法,将这a+b个相邻时刻的可靠度与构态切换时刻可靠度Rct连乘,即定义了约束变胞机构单次构态切换成功的区间可靠度为
式中:R1i为第I 构态第i个相邻时刻的可靠度;R2i为第Ⅱ构态第i个相邻时刻的可靠度。
5 折纸变胞机构计算实例
图8 所示为纸板折叠过程:第1 步从图8(a)到图8(b),纸板1 和纸板2 保持相对静止,沿2 与3 之间的折痕折叠成90°角。第2 步从图8(b)到图8(c),纸板2 和纸板3 保持相对静止,沿1 和2之间的折痕折叠成90°角。
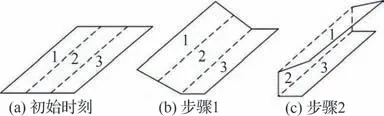
图8 纸板折叠过程Fig. 8 Folding process of a cardboard
一种可以执行整个折纸过程的两自由度平面约束变胞机构的运动简图如图9 所示。该机构可以拆分为主动件,RRR 杆组和RRRP 杆组。利用RRRP 杆组可以实现曲柄滑块机构和曲柄摇杆机构的切换。

图9 折纸变胞机构工作构态Fig. 9 Working-stage of paper folding metamorphic mechanism
折纸机构的结构参数如表1 所示,部分运动学参数变化范围如表2 所示。其中k1、k2、a、b分别为弹簧1 和弹簧2 的刚度及原长;d1、d2为弹簧1在连杆EF和连杆CE上安装位置与变胞副E回转中心的距离;ω1为主动件角速度;θ1为主动件的角位置;α为变胞转动副几何约束角度(∠CEF最大角度);Δθ1为主动件转角误差。假设表1 中各参数输入误差均服从正态分布,且其均值和标准差参照“3σ”原则给出。
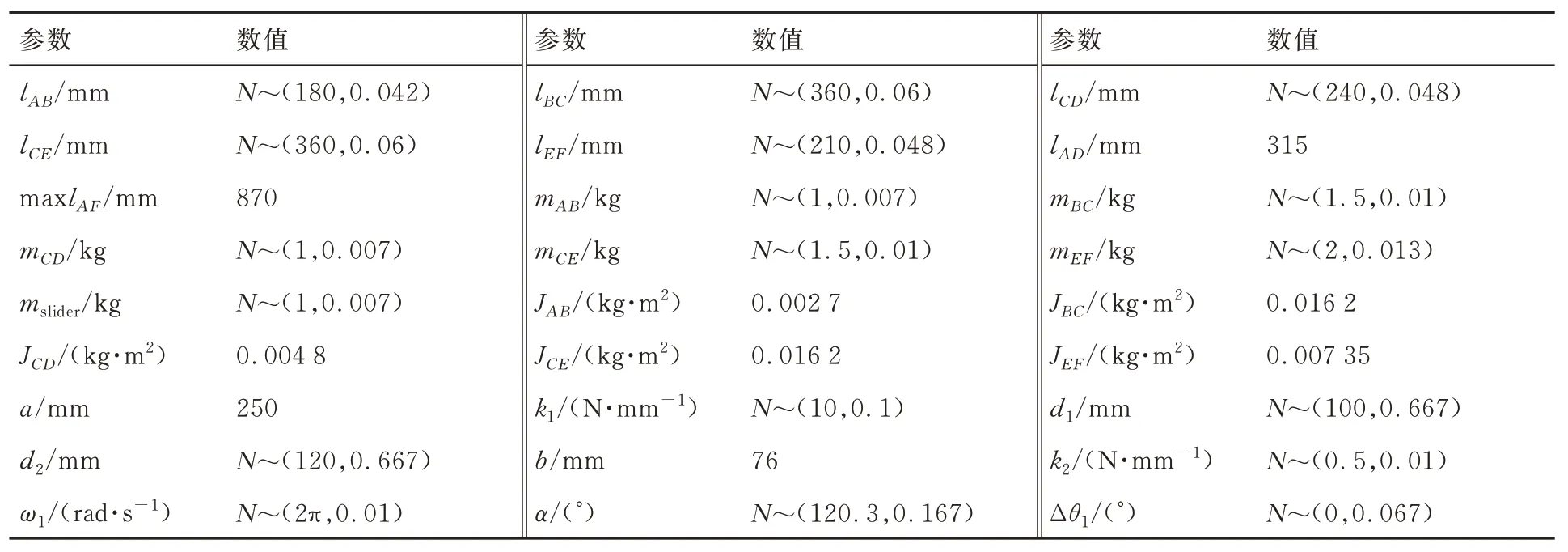
表1 折纸机构结构参数及公差Table 1 Structural parameters and tolerances of paper folding mechanism

表2 折纸机构部分运动学参数变化范围Table 2 Variation ranges of kinematic parameters of paper folding mechanism
基于理论计算模型并应用Matlab 对折纸变胞机构的运动学分析和力学分析进行编程计算,并通过ADAMS 仿真对部分Matlab 计算结果进行验证,两种方法计算结果对比如图10 和图11所示。
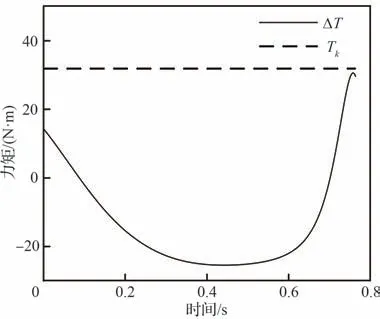
图10 第Ⅰ构态变胞转动副E的驱动力矩ΔT和约束力矩TkFig. 10 Driving torque ΔT and constraint torque Tk of metamorphic revolute joint E in working configuration Ⅰ
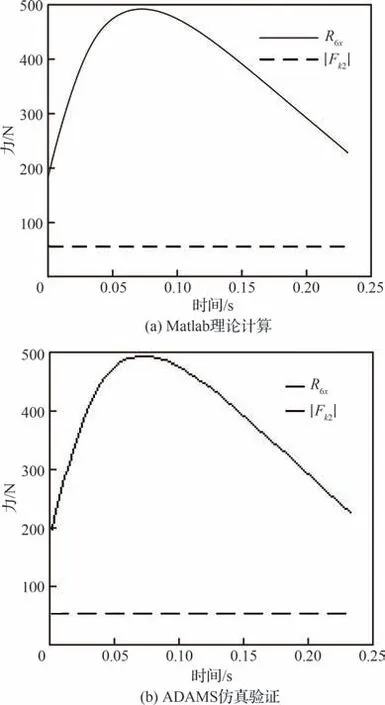
图11 第Ⅱ构态滑块所受支反力R6x和弹簧力Fk2Fig. 11 Reaction force R6x and spring force Fk2 of slider in working configuration Ⅱ
变胞副E和G等效阻力系数fE和fG如图12(a)所示,fE在第I 构态临近构态切换时刻的局部放大图如图12(b)所示。其中θi为局部放大图的边界角位置,θj和θk分别为不可靠工作区的极限角位置。受表1 中各参数误差影响,这一时间段内变胞转动副RE的运动状态切换很可能被提前或滞后,造成运动时序错乱。

图12 折纸机构等效阻力系数Fig. 12 Equivalent resistance coefficients of paper folding mechanism
基于计算式(25)和式(27),利用蒙特卡洛法随机抽样106次,计算构态切换时刻变胞副E的等效阻力系数频数直方图见图13(a),在正态分布概率纸上的检验曲线见图13(b),分布为线性表明这一时刻等效阻力系数呈正态分布。

图13 等效阻力系数fE构态切换时刻频率直方图和Q-Q图Fig. 13 Frequency histogram and Q-Q diagram of equivalent resistance coefficient fE at the moment of configuration transformation
基于4.2 节中推导的构态切换能力的概率评估模型,构态切换时刻及其相邻时刻可靠度理论计算结果和蒙特卡洛仿真结果如表3所示。
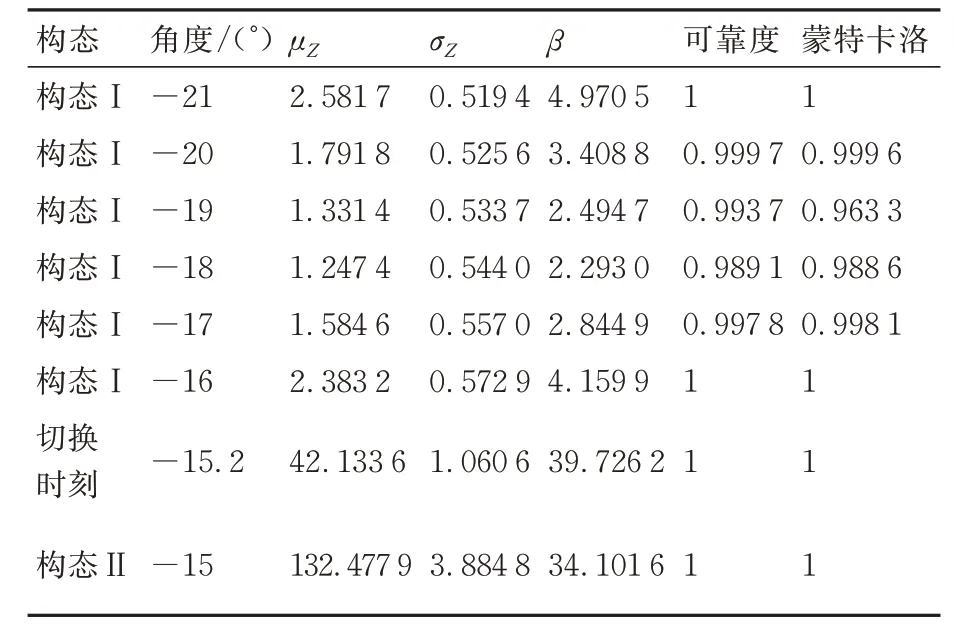
表3 可靠度理论计算和蒙特卡洛仿真结果Table 3 Theoretical calculation and Monte Carlo simulation results of reliability
由式(34)得,折纸机构的构态切换能力的区间可靠度为
6 讨 论
1)为了使本文提出的可靠性评估模型更具一般性,假设所有输入误差随机变量均符合正态分布。对于一些符合其他分布类型的误差随机变量可以通过等效正态化处理[30]将其转化为符合正态分布的随机变量,进而利用提出的可靠性分析模型开展构态切换能力的概率评估。
2)建立的构态切换能力的概率评估模型本质上是基于受力分析的,然而运动副间隙的存在会引起变胞副驱动力矩的波动,进而引起等效阻力系数的波动,最终影响概率评估结果。因此,提出的概率评估模型是仅考虑理想状态下的力学模型,具有一定局限性。
3)显然,约束变胞机构在构态切换时刻以及各相邻时刻的运动失效存在相关性。然而在建立构态切换区间可靠度计算模型时,直接采用了理想条件下串联系统的可靠度计算方法,忽略了相关性的影响。因此,提出的构态切换区间可靠度计算方法是在一定允许条件下的近似计算。
7 结 论
1)利用建立的变胞杆组模块化受力分析模型提出了变胞转动副的约束参数设计方法并设计了一种新型包含弹簧力-几何组合变约束的变胞转动副的结构形式。
2)基于变胞副等效阻力系数的定义和计算,完成了确定性条件下约束变胞机构构态调控的力学机理建模。在确定性模型中,考虑输入误差的随机性,建立了描述平面约束变胞机构构态切换能力的概率评估模型。首先,基于应力-强度干涉模型提出了变胞副运动状态切换的可靠度计算方法,进而建立了约束变胞机构构态切换时刻的可靠性评估模型。最后,考虑构态切换相邻时刻运动功能失效的影响,利用系统可靠性理论建立了构态切换的区间可靠度计算模型。
3)以折纸变胞机构的设计计算为例,验证了论文提出的平面约束变胞机构构态切换概率评估方法的可行性和有效性。可靠性分析结果表明:构态切换时刻,变胞转动副的等效阻力系数 满足均值μ=0.43、方 差σ2=1.21×10-6的 正态分布,构态切换成功的时刻可靠度R=1、区间可靠度R=0.980 4。针对变胞机构构态切换能力提出的概率评估方法,也能为折展机构、多模式机构等具有可变工作构态属性机构的构态切换能力评估提供借鉴和参考。同时,为进一步推动变胞机构在航空航天领域的实际工程应用提供基础理论和设计依据。

