弹性机翼阵风减缓控制策略风洞试验
曾宪昂,赵冬强,李俊杰,严泽洲,刘成玉
航空工业第一飞机设计研究院 强度设计研究所,西安 710089
强烈的阵风和湍流会给飞机带来不可忽视的附加气动力和气动力矩,使机体结构承受的载荷增加,缩短结构疲劳寿命[1]。同时,阵风引起的机体颠簸会大大降低乘员和乘客的乘坐舒适性甚至会干扰飞行员的正常操作,影响飞行安全[2]。为了减轻阵风干扰,提升飞机性能,阵风减缓技术为很多机型所采用[3-6]。
阵风响应和减缓控制研究的主要模态是集中了绝大部分阵风激励能量的刚体运动模态和若干阶低频弹性模态[7]。刚体运动的阵风减缓主动控制策略主要分为2 类。一类是将机体过载等信号反馈给作动系统,指令操纵面偏转的闭环反馈控制,如A320 飞机采用的载荷减缓功能系统(Load Alleviation Function,LAF)[8]。另一类是基于精确阵风探测的开环前馈控制[9],通过探测前方风场信息使飞机在充足的反应时间内控制操纵面偏转,将紊流对机体的影响减至最低。多普勒激光雷达利用发射和反向散射光的多普勒频移效应测量气流和机体的相对运动速度,因其具有测量精度高、时空分辨率高、测量范围广、响应速度快等特点,被广泛应用于远程风场的数据探测[10]。RABADAN 等[11]研发了一种机载紫外线多普勒激光紊流探测装置,可探测机头前50 m,10°视角内的空间阵风场,该装置在A340-300 飞机上安装并完成飞行测试。此外,德国宇航中心的ATTAS 验证机的载荷减缓和乘坐改善系统(Load Alleviation and Ride Smoothing System,LARS)对刚体运动的减缓也采用了开环前馈控制技术[12]。对弹性模态的阵风减缓大多使用闭环控制[13-14],通过将弹性振动信号反馈给作动系统使操纵面做卸载偏转从而降低载荷。例如C-5A 飞机的主动升力分布控制系统(Active Lift Distribution Control System,ALDCS),利用副翼和升降舵对翼尖过载的反馈偏转重新分布了机翼载荷,减小了翼根弯矩增量[4]。基于阵风探测的弹性模态开环阵风减缓的研究相对较少,ZHAO 等[15]对研究了某大型运输机弹性机翼自适应前馈阵风减缓控制器设计。
风洞试验是开展阵风减缓控制研究的一种有效手段,可为设计和分析提供必要的验证和修正数据。目前大多数阵风减缓风洞试验是基于闭环反馈的控制策略开展的[16-19]。杨俊斌等[18]对飞翼布局飞机的多种经典控制方案开展了风洞试验研究,BI 等[19]通过风洞试验研究了通过压电装置抑制大柔性机翼阵风响应的效果。本文以某弹性飞机缩比模型的大展弦比机翼为研究对象,研究闭环反馈和开环前馈2 种减缓机翼弹性振动阵风响应的控制策略,并构造原理性风洞试验进行验证。闭环控制是通过将翼尖振动速度反馈给副翼偏转实现的。速度反馈的作用等效于增大弹性模态阻尼从而降低结构的阵风响应峰值,和传统的过载反馈控制相比作用更直接且具有更好的高频稳定性。有别于大多数关注飞机刚体运动减缓的开环控制研究,本文侧重于研究前馈控制对机翼低阶弹性模态的阵风减缓。在开环控制试验中使用五孔探针模拟阵风探测装置,阵风速度实时前馈给副翼使其延迟作动以抑制阵风响应,前馈增益和延迟时间由实测响应对比法获取。通过试验结果分析2 种控制策略对机翼阵风响应的减缓效果并对比分析它们的优点和不足,为工程设计提供参考。
1 阵风减缓控制策略
如图1 所示,大型运输类飞机的大展弦比机翼是阵风敏感部件,当它遭遇湍流时在扰动气动力作用下会产生振动并带来额外的翼根弯矩增量,位于外翼的副翼偏转可产生可观的弯矩起到减轻载荷的效果。为研究弹性机翼阵风减载的控制策略,建立考虑阵风扰动的弹性机翼频域运动方程,如式(1)所示。
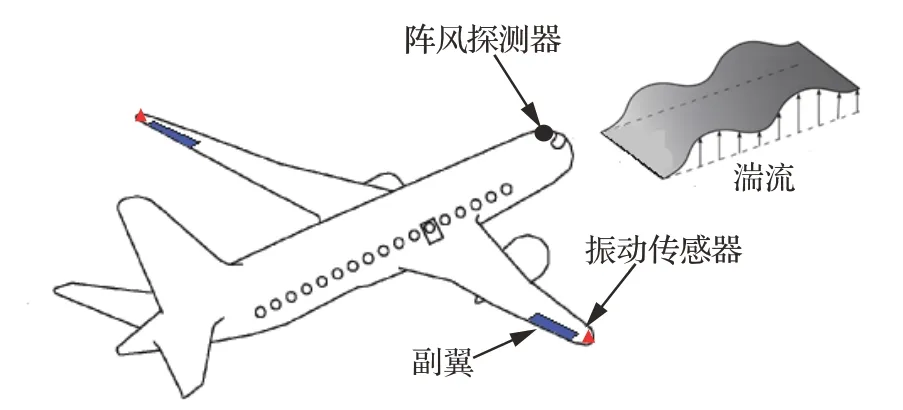
图1 湍流遭遇示意图Fig. 1 Sketch of turbulence encounter
式中:ω为振动圆频率,q、δa、wg分别为模态广义坐标、副翼偏角和垂向阵风速度;Mqq、Cqq、Kqq分别为广义质量矩阵、阻尼矩阵和刚度矩阵;Fq、Fδ、Fg分别为弹性模态、副翼偏角和垂向阵风产生的广义气动力向量。
第1 种控制策略是模态阻尼增强的阵风减缓(Modal Damping Enhanced Gust Alleviation,MDEGA),其控制框图如图2 所示,H(s)为反馈控制器传递函数,s为拉普拉斯变量。由振动传感器感知翼尖垂向振动速度,该信号经增益K反馈给副翼,同时在反馈回路中视情串联低通滤波器和陷幅滤波器以保证气动伺服弹性稳定性。
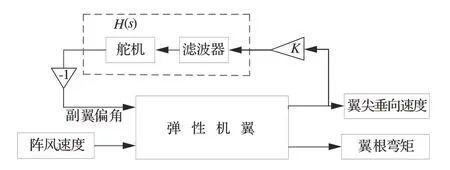
图2 MDEGA 控制框图Fig. 2 Control block diagram of MDEGA
速度比例反馈等效于为结构模态增加运动阻尼。当结构共振时惯性力和回复力平衡,振动速度和外力是同相或者反相的,这时使用适当增益的比例速度反馈可使控制力持续对结构做负功以最大限度地耗散振动能量。需要指出的是传统过载反馈控制中当加入滤波器等环节后也能在某些共振点将控制力相位调节到与振动速度同相或反相从而起到很好的振动减缓效果,然而相比之下速度反馈的形式更简单、作用更直接。此外,和过载反馈相比,速度反馈具有更好的高频稳定性,这是因为在相同反馈增益下速度比例反馈回路的开环传递函数幅值是过载比例反馈回路的ω-1。因此,使用速度反馈控制可以减少滤波器的使用,控制器阶数更低。
第2 种控制策略是基于阵风感知的阵风抑制(Gust Sensing Based Gust Suppression,GSBGS),控制框图如图3 所示,其原理是利用副翼偏转产生的气动力增量抵消阵风气动力。前场探测阵风传播至机翼翼面存在时间延迟,延迟时间为L/V,其中L为阵风测点到设计阵风参考点(通常取机翼气动中心)的距离,V为飞行速度。设计控制律δa=Gδgwg(Gδg为副翼偏角对垂向阵风速度的传递函数),使式(1)中的控制力Fδ和阵风气动力Fg相抵消。GSBGS 属于开环系统,其优点是不改变受控对象的动态特性。

图3 GSBGS 控制框图Fig. 3 Control block diagram of GSBGS
2 研究对象
本文研究对象是某运输类飞机全机动力学缩比风洞试验模型的大展弦比弹性机翼,翼展为4.4 m,展弦比为9.6。图4 给出了全机试验模型在风洞中的安装图。试验模型各部件的刚度由变截面铝合金梁模拟,翼面及机体切分成若干段,采用木制结构维形,每段与金属梁单点连接。机身上安装有滑块和转盘轴承,用于实现试验件上下沉浮和俯仰运动。模型的控制面共6 块,包括左/右副翼、左/右升降舵和左/右快速襟翼,每块舵面由单独的伺服电舵机驱动。在翼尖附近沿垂向安装振动加速度计。在翼根处沿翼梁方向粘贴应变片,测量应变进而转换成该点所承受的弯矩,转换系数通过载荷标定试验给出。在机身俯仰轴附近安装有倾角传感器用于测量机体俯仰角;在滑块上安装位移传感器以测量机体沉浮位移。在风洞中安装了五孔飞行探针,靠近机头左侧,探头与机头前端沿气流方向对齐,用于测量阵风速度。机身上安装前后2 根钢索,沿竖直方向引出洞顶与悬吊弹簧相连,通过悬吊机构调整模型位置使机身水平,距下壁面2.5 m。试验拟分2 阶段开展:第1 阶段是机翼弹性模态阵风响应的减缓策略原理研究;第2 阶段是全机刚/弹模态阵风减缓原理研究。本文围绕第1 阶段的研究展开介绍和讨论。

图4 风洞和试验模型Fig. 4 Wind tunnel and test model
试验件的有限元模型如图5 所示,金属梁架采用实体单元模拟;维形框、蒙皮和长桁采用板单元和梁单元模拟;配重用集中质量单元模拟。表1 给出了模型主要对称模态的计算频率和地面共振试验值的对比。机翼最低阶弹性模态是垂直一弯模态,其固有频率小于垂直二弯模态频率的1/3,是机翼对阵风最敏感的弹性模态。

图5 有限元模型Fig. 5 Finite element model

表1 试验模型主要对称模态频率Table 1 Main symmetrical modal frequencies of test model
3 试验风洞和阵风发生器
试验在FL-10 低速风洞中开展,试验段截面尺寸为8 m×6 m。阵风发生器由沿高度方向布置的4 组弦长0.5 m、展长6 m、剖面翼型为NACA0015 的长直叶片组成,叶片高度间距0.7 m,如图6 所示。试验模型安装在阵风发生器的尾流区,机头距发生器叶片后缘3 m。每组叶片由独立的液压马达驱动,试验时驱动阵风发生器叶片在不同频率下做简谐偏转运动,产生同频率的垂向阵风。试验模型安装前,在风速V=20 m/s 测量模型理论气动中心所处风洞横截面的阵风速度,该截面位于阵风发生器后缘下游xs=5.8 m。图7 显示了叶片摆幅B=2°,频率F=3.0 Hz,截面中心处的阵风速度波形图,由于湍流和气动非线性等因素的影响,阵风波形并不是理论正弦,但主要能量集中在叶片偏转频率下,幅值谱如图8 所示,可近似视为正弦阵风。xs=5.8 m 截面上纵向和横向若干位置的阵风幅值在图9 中给出。图中ys表示测点与截面中心的横向距离,顺流向左侧为正;zs表示测点与截面中心的纵向距离,向上为正。可以看出相同叶片摆幅下阵风幅值随频率的增大而增大;在距离风洞中心0.5 m 高度范围内阵风速度幅值变化小(<5%),当偏离截面中心高度1.0 m 时,阵风速度较中心位置下降了8%~13%;横向2.7 m 站位阵风幅值较中心位置下降了13%~26%,这是因为在相同迎角下等直翼段的附着涡和尾涡强度从根部到尖部是逐渐减弱的。

图6 阵风发生器Fig. 6 Gust generator
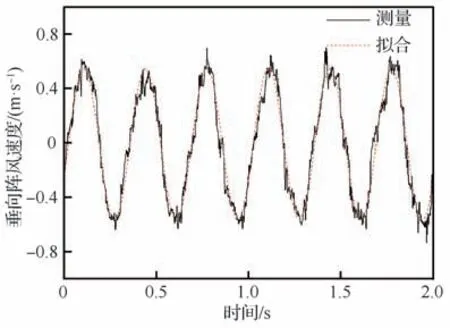
图7xs=5.8 m 截面中心垂向阵风速度响应 (V=20 m/s,F=3.0 Hz,B=2°)Fig. 7 Gust velocity response at the center of section xs=5.8 m (V=20 m/s, F=3.0 Hz, B=2°)
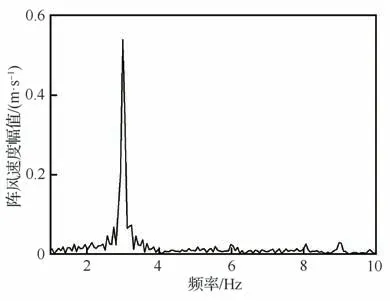
图8 阵风速度的幅值谱(V=20 m/s,F=3.0 Hz,B=2°)Fig. 8 Amplitude spectrum of gust velocity (V=20 m/s, F=3.0 Hz, B=2°)
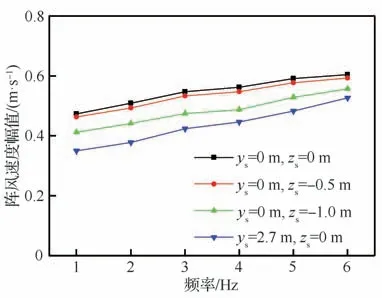
图9xs=5.8m 截面若干位置阵风速度幅值(V=20 m/s,B=2°)Fig. 9 Gust velocity amplitude at several positions of section xs=5.8 m (V=20 m/s, B=2°)
4 主动控制系统
主动控制系统由仿真软件、仿真机、信号转接箱、传感器和电动舵机等组成[20],如图10 所示。在仿真软件RT-Sim 中建立仿真模型,并将所设计的控制律编译生成可执行程序下载到仿真机中。仿真机是主动控制系统的核心,它接收各传感器输出信号,对控制律进行实时解算,并向伺服舵机发出控制指令。仿真执行过程中可通过仿真软件与仿真机交互,实时变更控制参数,如控制增益、控制律切换等。

图10 主动控制试验系统结构图Fig. 10 Frame of active control system for test
5 风洞试验
5.1 刚体运动的响应测试
本期试验的目的是设计控制器以减缓机翼一弯模态附近频段翼根弯矩和翼尖法向过载的阵风响应。首先需要确认模型刚体模态频率,以选取刚体运动影响小的频段来开展测试,提高试验结果的可信度。在V=20 m/s 试验风速下驱动阵风发生器在0.3~6 Hz 内的不同频率下做摆幅B=2°的正弦运动,采集阵风测点位置的垂向阵风速度wgd、试验模型的沉浮位移H以及俯仰角θ信号,得到H和θ对wgd的幅频响应曲线如图11所示。
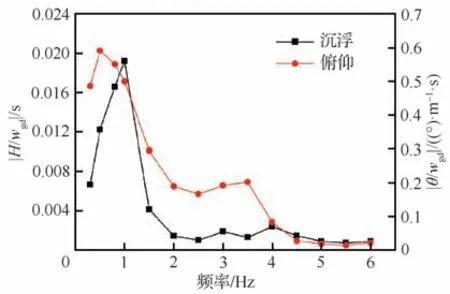
图11 刚体运动对垂向阵风速度的幅频曲线Fig. 11 Amplitude-frequency curves of rigid body motion to vertical gust velocity
可以看出俯仰和沉浮模态的主频分别在0.5 Hz 和1.0 Hz,当F≥1.5 Hz时刚体运动响 应相比峰值有明显降低,对弹性模态的影响小。因此试验频段选取在1.5~6.0 Hz,覆盖机翼一弯模态频率。下面分别介绍MDEGA 和GSBGS 控制器设计及试验实施效果。
5.2 MDEGA 控制设计及验证
5.2.1 MDEGA 控制器设计
由于在机翼上未安装速度传感器,需要对振动加速度信号积分来构造速度信号,并使用高通滤波器来消除积分引起的低频信号飘移,MDEGA控制器结构如图12 所示。图中az和vz分别表示机翼翼尖垂向加速度和速度,一阶高通滤波器和低通滤波器的截止频率分别为1 Hz (ω1=2π)和20 Hz (ω2=40π)。控制增益K越大减缓效果越佳,但同时需要兼顾气动伺服弹性稳定性的约束,副翼通道的幅值和相位裕度应分别不低于6 dB 和60°。定义副翼后缘下偏为正,根据仿真结果给出满足稳定性要求的增益K=20(°)/(m·s-1),控制器中无需增加结构陷幅滤波器。

图12 MDEGA 控制器Fig. 12 MDEGA controller
5.2.2 试验结果
在V=20 m/s 风速下,驱动阵风发生器做摆幅B=2°的正弦运动。在摆动频率F=1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5、6.0 Hz 下关闭和开启MDEGA 控制器分别完成阵风响应测试,翼根弯矩和翼尖法向过载增量的均方根随阵风频率的变化见表2 和表3。
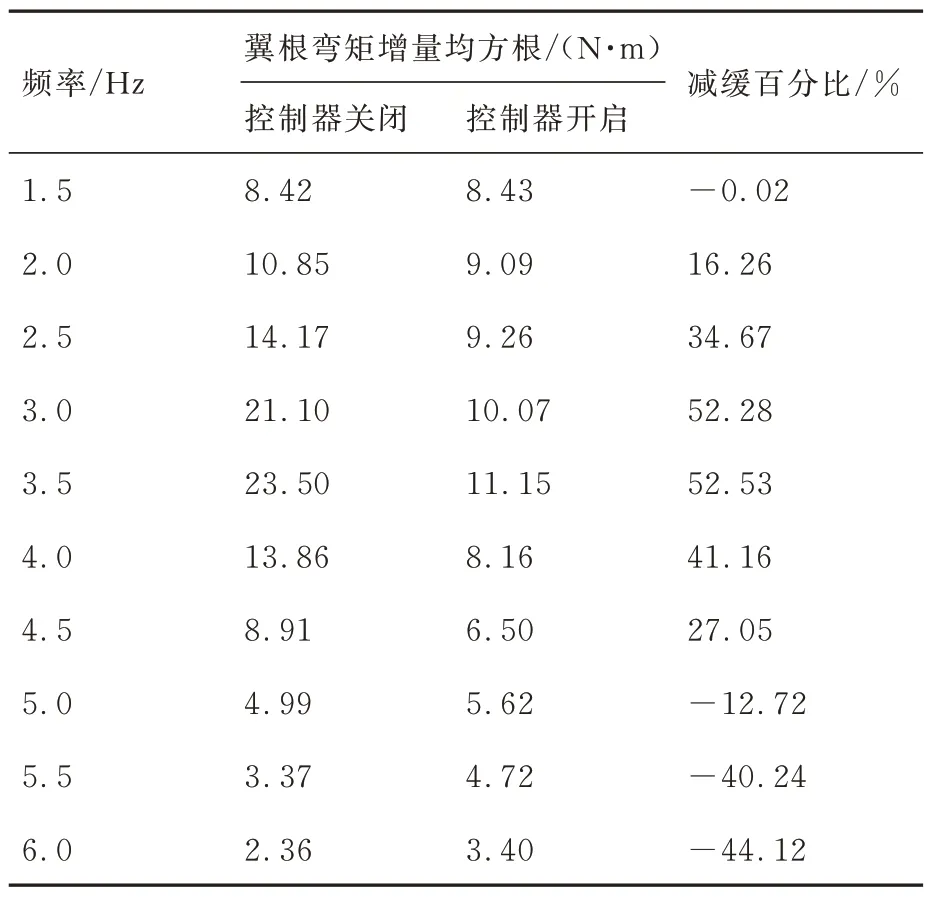
表2 MDEGA 控制器对翼根弯矩的减缓效果Table 2 MDEGA results for wing root bending moment

表3 MDEGA 控制器对翼尖过载的减缓效果Table 3 MDEGA results for wing tip acceleration
变量X的均方根计算公式为
式中:N表示采样数。
可以看出,无控状态机翼在3.5 Hz 频率下的阵风响应幅值最大,对应机翼对称一弯模态。MDEGA 控制器开启后翼根弯矩和翼尖过载响应在峰值附近的减缓效果显著,减缓百分比均超过了50%。图13 给出了F=3.5 Hz 时翼根弯矩增量、翼尖过载增量以及副翼偏角的响应历程。为验证闭环系统的稳定性,通过开环频响试验测得副翼通道的Nyquist 曲线如图14 所示,幅值和相位裕度分别为Gm=13.2 dB(对应于11.6 Hz)和Pm=90.9° (对应于4.74 Hz),满足气动伺服弹性稳定性要求。试验实测的系统稳定性略优于分析值(Gm=6.16 dB,Pm=109°)。产生差异的主要原因是理论模型和实物的振型差异。实物机翼的二阶弯曲模态节线更靠近振动测点,故在该模态频率附近的实测响应幅值小于理论值。
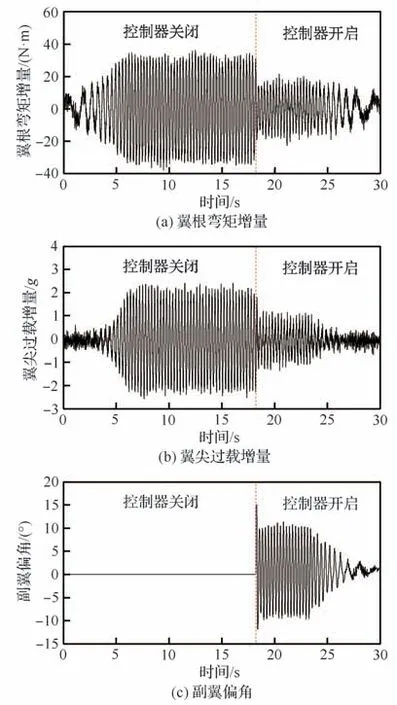
图13 MDEGA 关闭和开启状态机翼阵风响应历程(V=20 m/s,F=3.5 Hz)Fig. 13 Gust response of wing in condition of MDEGA off/on (V=20 m/s, F=3.5 Hz)
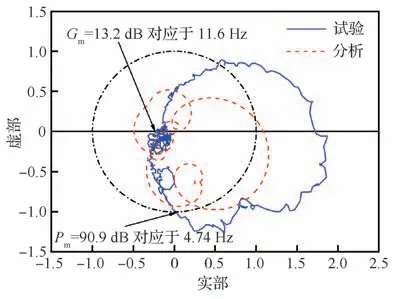
图14 副翼通道Nyquist 曲线Fig. 14 Nyquist curves of aileron loop
5.3 GSBGS 控制设计及验证
5.3.1 GSBGS 控制器设计
GSBGS 的原理是驱动副翼偏转产生大小相等方向相反的力矩来抵消阵风扰动力矩。控制器可运用理论方法确定,这里为减小实物和理论模型偏差的影响采用一种基于试验数据的响应对比法来设计控制器。即以翼尖过载为中间变量,分别测出它对垂向阵风速度和副翼偏角的频响曲线,利用幅值相抵、相位相反的抑制原理来确定控制律。即设计控制器δa=-D·C·wgd使得:
式中:wgd表示五孔探针测得的垂向阵风速度;Gag和Gaδ分别表示翼尖过载对垂向阵风速度和副翼偏角的传递函数;D=20π/(s+20π)为用于滤除高频振动和噪声信号的低通滤波器的传递函数;C为GSBGS 控制器传递函数。在频率ω下,传递函数的频响特性如下:
其中:Aag、Aaδ、AD分别为Gag、Gaδ、D的幅值;τag、τaδ、τD分别为该频率下Gag、Gaδ、D的响应延迟时间。将式(4)代入式(3)得:
式中:Ac和τc分别为控制器C的幅值和延迟时间。Gag和Gaδ的频响特性分别通过阵风和副翼步进正弦扫频试验测得。在V=20 m/s 风速下,Aag、Aaδ和Ac的对数幅频曲线如图15所示,τag、τaδ和τc随频率变化曲线如图16 所示。观察到在1.5~6.0 Hz频率范围内幅值Ac和延迟时间τc变化小,因此可将控制器C简化为一个时滞比例环节:C=Ke-τs根据F=3.5 Hz(20 m/s 风速下机翼对称一弯频率)的试验数据确定控制参数K=22.3(°)/(m·s-1),τ=0.04 s。时滞环节的物理意义是位于机翼前方的探针感知的阵风到达机翼表面存在时间差,副翼偏转应滞后于阵风输入。图17 给出了GSBGS 控制器框图。
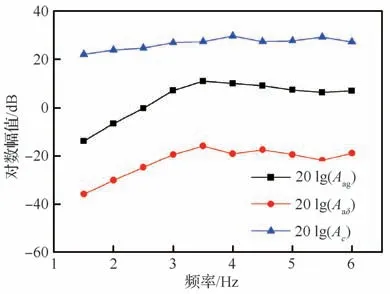
图15Aag、Aaδ 和Ac 对数幅频曲线Fig. 15 Logarithmic amplitude-frequency curves of Aag, Aaδ and Ac
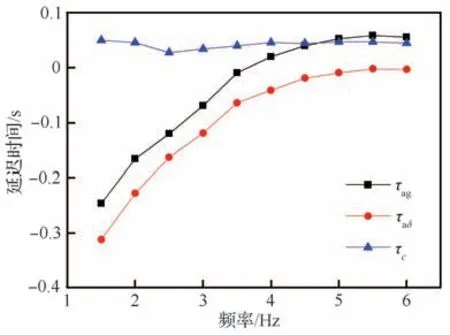
图16τag、τaδ 和τc 随频率变化曲线Fig. 16 Curves of τag, τaδ and τc with frequency

图17 GSBGS 控制器Fig. 17 GSBGS controller
5.3.2 试验结果
在V=20 m/s 风速下,控制阵风发生器做摆幅B=2°的正弦运动,摆动频率F范围为1.5~6.0 Hz,频率间隔0.5 Hz。关闭和开启GSBGS控制器分别完成阵风响应测试。控制器关闭和开启状态下翼根弯矩和翼尖法向过载增量的均方根随阵风频率的变化如表4、表5 所示。GSBGS 控制器在1.5~5.0 Hz 频率范围对翼根弯矩减缓百分比超过45%;在2.5~6.0 Hz 频率范围对翼尖过载减缓百分比超过48%。图18 显示了F=3.5 Hz 下垂向阵风速度、翼根弯矩增量、翼尖过载增量以及副翼偏角的响应历程。
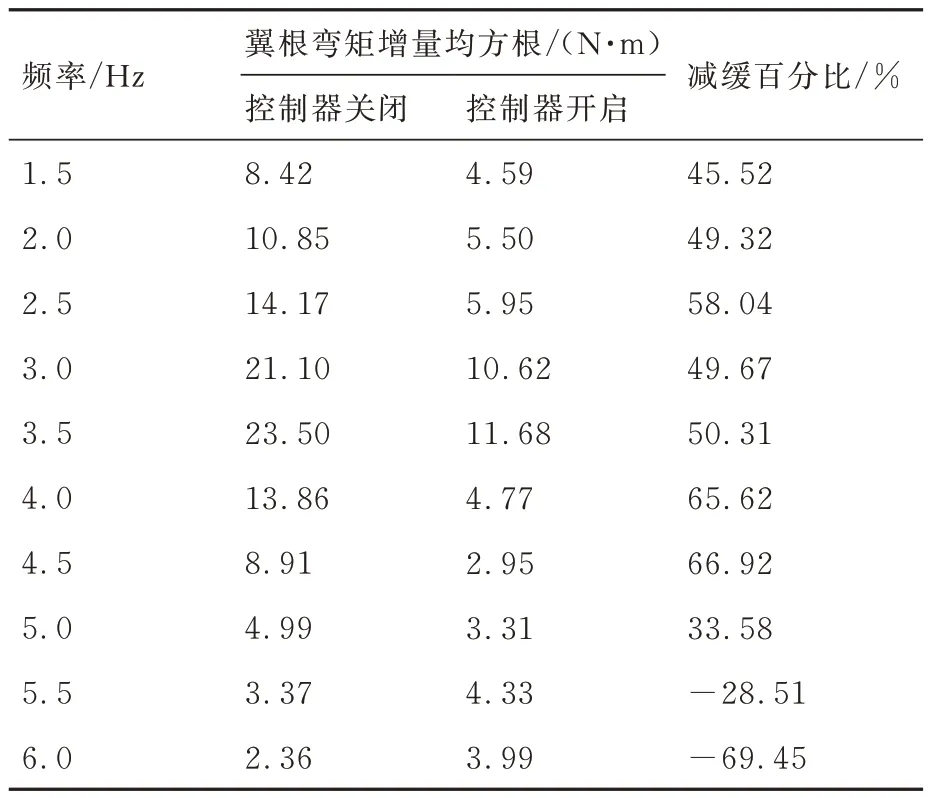
表4 GSBGS 控制器对翼根弯矩的减缓效果Table 4 GSBGS results for wing root bending moment
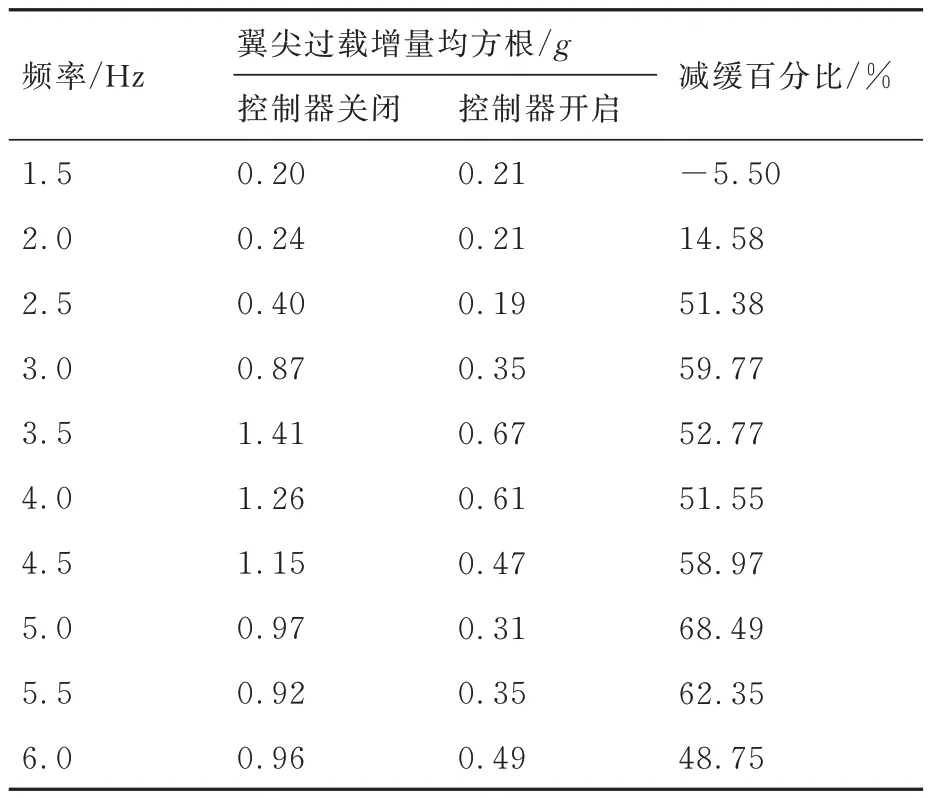
表5 GSBGS 控制器对翼尖过载的减缓效果Table 5 GSBGS results for wing tip acceleration
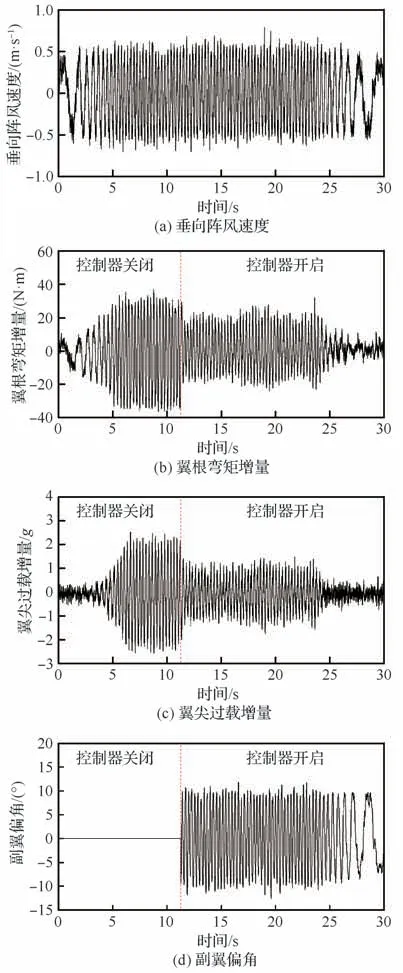
图18 GSBGS 关闭和开启状态机翼阵风响应历程(V=20 m/s,F=3.5 Hz)Fig. 18 Gust response of wing in condition of GSBGS off/on (V=20 m/s, F=3.5 Hz)
6 分析和讨论
无控、开启MDEGA 和开启GSBGS 这3 种状态下翼根弯矩和翼尖过载增量响应均方根的对比如图19 所示。可以看出2 套控制律对机翼一弯(F=3.5 Hz)响应峰值下的翼根弯矩和翼尖过载的减缓量均超过50%。MDEGA 控制器作用效果是“削平”振动响应峰值,这是因为在共振点处翼尖测点的垂向速度和阵风气动力是同相的,垂向速度比例反馈给副翼作动器,产生反相的控制力能够大幅削弱响应峰值。在非共振频率下阵风气动力和测点垂向速度存在一定相位差,只有部分舵面气动力分量能够起到能量耗散作用,因而减缓效果随着阵风频率和共振主频差量的增大而降低。与MDEGA 控制器相比,GSBGS 控制器能够在更宽的频率范围抑制机翼的阵风响应,试验结果显示翼根弯矩的幅频响应曲线在1.5~4.5 Hz,翼尖过载在2.5~6.0 Hz 范围内呈现出整体下降的趋势,并且3.5 Hz 处的共振峰依然是存在的。这是因为GSBGS 控制器的延迟时间τ体现的是阵风从探针探头传播至翼面形成气动载荷的时间差,和探针的位置及来流风速强相关,而和阵风频率是弱相关的,这点从图16 也能够看出来。
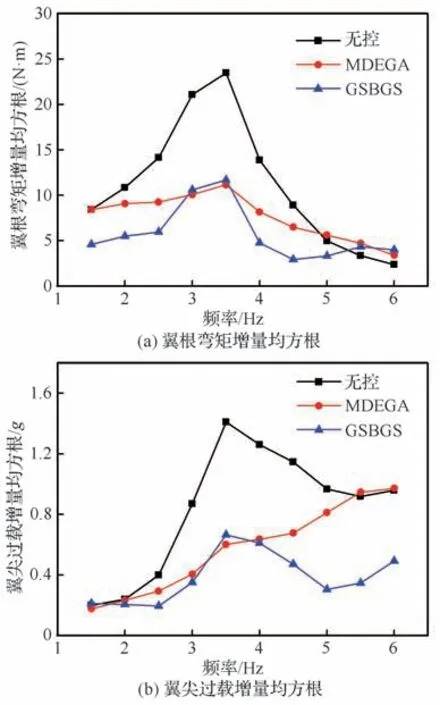
图19 MDEGA 和GSBGS 结果比较Fig. 19 Results comparison between MDEGA and GSBGS
MDEGA 控制策略的优点是不需要精确测量阵风,但是它的引入改变了飞机的动态特性[21]。因此,MDEGA 控制器设计时应考虑气动弹性稳定性问题;当机翼弹性模态频率较低时控制器可能会与刚体模态耦合从而影响操纵品质;此外,为减轻非关键模态的不利耦合需优化传感器位置。
GSBGS 控制策略最突出的优点是不改变飞机本身的动态特性,对操稳特性和气动弹性稳定性无影响,但其实现很大程度上依赖于阵风探测的精度。本次试验将阵风探测器安装在试验模型外,不受机体振动的影响。在工程中,当探测器安装于机上时,飞机的刚体运动和传感器安装点的局部振动会产生干扰信号叠加到所探测的阵风信号中,从而影响阵风减缓效果、飞机操稳特性、气动伺服弹性稳定性乃至危及飞行安全。因此,如何从测量信号中分离出阵风速度以及如何保证阵风减缓系统高可靠地工作是GSBGS 控制策略工程实现的关键。
弹性飞机的阵风减缓控制分析模型是多变量高阶复杂模型,它和实物之间不可避免地存在一定偏差[17],这些差异主要包括非定常气动力、模态特性、作动器特性[22]、非线性和系统延迟等,根据理论模型设计出的控制器不一定能够获得期望的减缓效果,甚至会出现反效的情况。本文研究过程中所采用的实测响应对比法可为工程设计所借鉴,借助飞行试验数据来设计控制律参数在一定程度上可降低理论模型偏差带来的技术风险。
7 结 论
通过原理风洞试验研究了MDEGA 和GSBGS 这2 种弹性机翼阵风减缓控制策略,结果表明2 种控制器对机翼一弯模态阵风响应减缓效果显著,在峰值频率处翼根弯矩和翼尖过载的减缓量超过了50%。2 种控制策略各有特点,总结如下:
1) MDEGA 改变了机体动态特性,提高了阵风敏感模态的运动阻尼,其作用效果是削弱振动响应峰值。控制器设计需综合考虑对操稳特性和气动伺服弹性稳定性的影响。
2) GSBGS 利用操纵力直接抵消阵风气动力,在一定频率范围内将阵风响应幅值整体降低。它是一种开环前馈控制律,不改变机体的动态特性,但依赖于阵风探测的精度和系统可靠性。
3) 实测响应对比法能够准确、快速地确定阵风减缓控制参数,提高设计效率并降低技术风险,工程中可用来辅助控制器设计。

