并行稀疏滤波在轴承声信号下的故障诊断

王金瑞，季珊珊，张宗振，2，*，初振云，韩宝坤，鲍怀谦

1．山东科技大学 机械电子工程学院，青岛 266590

2．南京航空航天大学 能源与动力学院，南京 210016

滚动轴承在航空发动机的传动系统中起着动力传输和支撑作用，由于其工作环境复杂多变，在连续工作状态下极易发生故障，且难以有效诊断。为了保证航空发动机的稳定运行，避免故障的发生，智能故障诊断方法引起了广泛关注［1］。

在这些方法中，振动信号可以清晰地描述故障特征，因此常被许多学者分析［2］。基于振动信号的技术称为接触式故障诊断。振动信号分析需要正确安装加速度传感器，这就要求传感器位置不能发生过大改变，否则就不能准确诊断故障。

航空发动机结构更复杂精密，对传感器的布置提出了更高的要求。在振动信号难以测量的情况下，声信号是一种被广泛应用的非接触信号。声学信号的采集相对容易，不需要预先粘贴传感器。因此不影响设备的正常工作，而且容易实现早期预后和在线监测。Zhang 等［3］将声学信号转化为具有几何结构的图形形式，构建了用于轴承故障诊断的深度图卷积神经网络。Glowacz［4］提出了一种简化的频率选择方法用于提取感应电机故障识别的声学信号特征。Liu 等［5］采用短时傅里叶变换将声信号转换为谱图，并使用堆叠稀疏自编码器进行特征提取和分类。Parvathi 和Hemamalini［6］采用扩张小波变换对声信号进行预处理，实现了三相感应电动机的故障识别。在上述方法中，不同的信号变换过程并不总是对所有信号都有效，而且也降低了诊断效率。同时传声器所测得的声信号通常含有大量的环境噪声，使得声信号的信噪比较低，即表示机器运行状态的有用信号受到环境噪声的污染。因此，有效的特征提取是声信号故障诊断的关键。

由于航空轴承的动力学特性复杂、原始信号含有大量干扰且具有强烈的非平稳性，使得浅层学习模型在故障诊断中过度依赖人工特征提取和信号预处理。稀疏表示是特征提取过程中的一个重要原则，为了准确地识别不同类型的故障，所期望的特征分布必须表现出种群稀疏性和存在稀疏性。稀疏滤波［7］是以优化特征的稀疏分布为目标的无监督学习方法，在接触式的故障诊断中得到了广泛应用。Lei 等［8］将稀疏滤波与Softmax 结合实现轴承故障分类。乔美英等［9］采用加权最小二乘法改进稀疏滤波目标函数来消除数据中异方差，实现减少训练时间并提升诊断准确率的效果。Zhang 等［10］提出对稀疏滤波的特征矩阵列做最小L1/2范数归一化，再对行做最大L1/2范数归一化来实现种群稀疏和存在稀疏。随后Zhang 等［11］提出快速卷积稀疏滤波对样本特征优化，从而降低了Hessian 矩阵维数和构造时间，输出特性也同样被激活以保证所有特性都具有相似贡献。An 等［12］通过消除经稀疏滤波训练的权重矩阵的多相关特性，减少了测试中的过拟合现象。Cheng 等［13］提出一种变体稀疏滤波，通过添加稀疏性参数来选出最优特征分布。An等［12］在稀疏滤波目标函数中加入L1/2范数，实现了变转速下的故障诊断。尽管上述方法诊断结果较为理想，但输入数据集均为振动信号。通过声学信号很难达到如此高的精度。另外，原始稀疏滤波需要先对特征矩阵的每一行进行归一化，然后再对每一列进行归一化。这可能会导致一些固有特征的泄漏，也就是说一些特征应该保留在列规范化中，但是通过行规范化被规范化为零。

提出一种基于并行稀疏滤波的无监督学习方法来提取声信号下的稀疏特征。该方法的网络训练中同时进行了两个并行的归一化过程：行→列、列→行。这样可以保留更多的固有特征，并消除更多无用的特征。因此提取的特征变得更加稀疏，对故障分类更加有效。

1 理论背景

1.1 稀疏滤波

稀疏滤波是一个简单的非监督两层网络用于学习指定特征，并不是尝试模拟数据分布，而是通过使用二范数特征来进行优化一个代价函数［13］。稀疏滤波模型学习完美的特征表示具有3 个原则：种群稀疏、存在稀疏和高分散性。

稀疏滤波的结构如图1 所示，输入为采集的信号，输出为学习到的特征。采集到的信号被分成许多相同的样本以此来组成1 个训练集，其中xi=RN×1是一个样本，M是样本个数。样本通过使用权值矩阵W∈RN×L映射到特征向量fi∈RL×1上：

图1 稀疏滤波结构Fig. 1 Structure of sparse filtering

特征值fij组成一个特征矩阵，如图2（a）所示，先归一化每个特征为相等的激活值，将每一个特征除以其在所有样本的二范数：

然后，每一列再通过二范数进行归一化，如图2（b）所示，其落在二范数的单位圆体上：

图2 稀疏滤波行列归一化过程Fig. 2 Row and column normalization process of sparse filtering

最后，对归一化的特征采用L1范数惩罚来约束稀疏性，如图3 所示。当一个数据集有M个样本时，稀疏滤波的目标函数表示为

图3 归一化方向Fig. 3 Normalization direction

在实践中，最常用和研究的稀疏度测度是作为稀疏度惩罚项或目标函数。Lp范数被定义为

Niall 和Scoot［14］比 较了16种常用的稀疏度度量，结果表明，pq-均值（p≤1，q＞1）可以满足所有理想特性标准，其表示一个可泛化的稀疏性度量族，它是广义p和q均值的比值：

式中：p＜q。

Jia 等［15］提出将如式（7）所示的L1/2归一化为pq-均值的特殊形式：

在稀疏滤波算法中，对于每个固定维度的训练样本，其目标函数可以表示为一种特殊形式的pq-均值测量Jsp，即p=1，q=2。故标准稀疏滤波器的目标函数可以写为

式中：p=1；q=2。

因此，二范数归一化以后求一范数从数学上可以看作为L1/2范数。此时最小化该范数可以获得稀疏特征。因此，标准稀疏滤波的目标函数还可以表述为：对特征矩阵行进行二范数归一化，最后求矩阵（每列）的L1/2范数。

1.2 并行稀疏滤波

并行稀疏滤波在现有稀疏滤波的基础上增加了另一个归一化方向，与原始稀疏滤波的对比如图3 所示，即在原有“行→列”归一化的基础上添加了“列→行”归一化。如图4 所示，首先，对所有列进行二范数归一化，将特征值映射到单元二范数球体中，使其平方激活值为1：

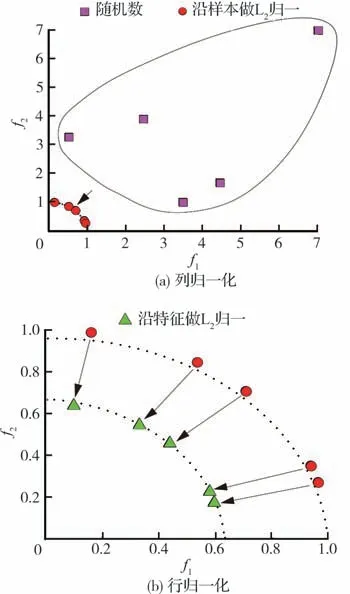
图4 并行稀疏滤波列行归一化过程Fig. 4 Column and row normalization process of parallel sparse filtering

然后，所有行被归一化，同等被二范数激活：

随后，利用L1惩罚对计算得到的特征进行优化，该方向的目标函数为

式中：N为样本维数。

将式（4）与式（7）整合得到并行稀疏滤波的最终目标函数为

式中：λ≥0 控制这两项之间的权衡。

最后，采用L-BFGS 算法［16］对式（8）进行优化，梯度函数为

式中：o∈RN×M为1 的矩阵；x为输入数据。

这样并行稀疏滤波可以通过2个不同的归一化方向保留更多的输入信息，也为从噪声信号中提取更多有用信息提供了另一个约束。稀疏滤波和并行稀疏滤波的本质区别在于前者关注样本之间的稀疏性约束来实现判别，而后者同时考虑样本和特征之间的稀疏性。因此，并行稀疏滤波可以通过2 个不同的归一化方向提取比稀疏滤波更稀疏的特征。

2 仿真研究

采用仿真轴承外圈故障的振动信号［17］来展示并行稀疏滤波在噪声条件下的特征提取性能。因声信号是以振动信号为基础，物体声压级的变化等于物体振动速度级的变化，声振信号具有良好的相关性。由于振动信号到声学信号需经结构-空气的传递函数，直接模拟声信号难度很大。虽然振动信号在幅值分布上会受到复杂传递路径的影响，与声信号有一定的误差，但其频率分布不会改变。因此，在振动仿真信号的基础上添加噪声（信噪比为-12 dB）的可有效刻画出声信号的频率分布，不会改变滤波器的频率特性，有效验证滤波器训练这一过程。其数学表达式为

式中：Ai为一轻微的随机波动；B（t）为振幅调制；Su（t）为单位阶跃函数；Tg为脉冲间的时间间隔；δT表示滚动元件激发的随机抖动；n（t）为噪声分量；fr为谐振频率；a为脉冲衰减系数。模拟信号的参数设置如表1 所示。

表1 仿真信号参数设置Table 1 Parameter setting of simulation signal

此外，为了模拟工程实际，对模拟信号添加一脉冲性噪声：

式中：P为噪声幅值；fp为脉冲谐振频率。

图5（a）为原始信号及其包络谱，时域和频域信号的脉冲分量清晰可见。图5（b）为添加了高斯白噪声和工程脉冲性噪声的模拟信号。利用并行稀疏滤波和稀疏滤波对噪声信号进行滤波：将仿真信号进行随机分段后直接输入到模型中进行训练，再对得到的权值矩阵所有行向量做快速傅里叶变换即得如图6 所示的滤波器组。在本模型中，权值矩阵的本质是一个滤波器组，可完成对输入信号的子带分解，提取主要特征。图中右侧小图即是左侧图中对应的最优滤波器小波的时域和频域波形图。从图6（a）可以看出，并行稀疏滤波得到的第15 个滤波器具有明显的频率分量，对应的波形也表现出窄带特性。但是稀疏滤波得到的滤波器组并不理想，如图6（b）所示。仅第8 个滤波器显示出轻微的频率成分，但干扰频带相当明显。用得到的滤波器对噪声信号进行滤波，结果如图7 所示。如图7（a）所示，并行稀疏滤波可以成功滤除噪声成分，并显示出主要的脉冲信息。同时，在包络谱中可以发现明显的特征频率和谐波。但是，稀疏滤波的结果并不理想，如图7（b）所示。因此，并行稀疏滤波方法比稀疏滤波方法更能有效提取噪声信号的主要特征分量。

图5 仿真信号及其包络谱Fig. 5 Simulation signal and its envelope spectrum

图6 经不同模型训练得到的滤波器组Fig. 6 Filter groups trained by different models

图7 经不同模型滤波后的实验结果Fig. 7 Experimental results filtered by different models

3 故障诊断方法框架

所提出的基于并行稀疏滤波的轴承智能故障诊断框架如图8 所示，具体流程如下：

图8 所提方法流程图Fig. 8 Flow chart of the proposed method

步骤1采集原始声信号作为输入样本，每个样本经重叠取样得到Z个分段构成输入矩阵Tj∈RNin×Z，其中，j为第j个样本，Nin为并行稀疏滤波的输入维数。

步骤2将矩阵T直接输入到并行稀疏滤波中训练权值矩阵W。

步骤3采用L2范数对训练得到的权值矩阵进行归一化处理。

步骤4将xi平均分成K段并组成矩阵xi∈RNin×K，其中K=N/Nin。随后用权值矩阵W映射xi得K个局部特征fik∈RNout×1，其中，Nout表示并行稀疏滤波的输出维数。激活函数采用绝对值函数，式（1）可推广为

步骤5对所有局部特征分段求平均获取样本最终的学习特证：

步骤6将所有带标签数据的特征向量组合起来训练Softmax 回归分类器，并使用剩余样本进行测试［18］。Softmax 回归的假设形式为

式中：yi∈{1，2，…，k}为标签集；p(yi=j|x)表示xi的可能性，θ1，θ2，…，θk表示模型参数。

Softmax 的代价函数表示为

式中：1｛·｝为指标函数；m为样本量；k为类别数。

步骤7对测试样本平均分段经W映射得学习特征，输入训练好的Softmax 分类器获得测试准确率。

4 实验验证

轴承故障实验数据来自山东科技大学［19］，轴承座及声传感器布置如图9 所示，将声传感器安放在轴承座侧面10 cm 处，传感器连接LMS SCADAS 信号采集仪进行信号采集，并通过LMS Test. Lab 进行信号处理。声学传感器采集了轴承正常（NC）、外滚道故障（OF）、内滚道故障（IF）和滚子故障（RF）4 种不同健康状态下的声信号，采样频率25.6 kHz。3 种轴承故障模式如图10 所示。每种故障模式设置3 种不同的损伤级别（0.18、0.36、0.54 mm）。共收集10 种轴承健康状况，每种健康状况包含100 个样本，每个样本包含1 200 个数据点。此外为了模拟实际工况，对每种轴承健康状况信号添加脉冲噪声。现展示1 组正常与3 组故障轴承声波时域波形及其频谱和包络谱图如图11 所示：轴承的转频fR=166 Hz，在图11（c）中的包络谱中可以看出正常轴承的2 倍和3 倍转频特征，内圈故障特征频率fI=830 Hz，外圈故障特征频率fO=499 Hz，滚柱故障特征频率fB=415 Hz。此外还有一些其余的干扰频率也被激起，考虑是由于声信号自身信噪比低的原因所致。

图9 轴承座及传感器布置Fig. 9 Bearing set and sensors layout

图10 3 种轴承故障类型Fig. 10 Three bearing fault types

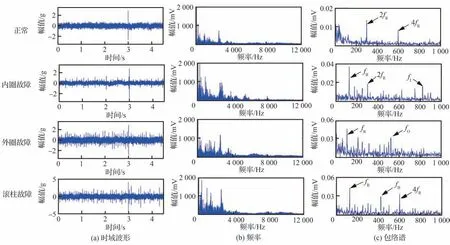
图11 轴承故障信号波形图Fig. 11 Waveforms of all bearing health conditions

采用所提方法对轴承声信号数据集进行处理。并行稀疏滤波的输入和输出维度均为100，λ参数设为0.1，迭代次数为200。随机抽取50%样本组成训练集，每个样本通过重叠分段的方式收集50 个分段。然后将这些分段输入到并行稀疏滤波中训练权值矩阵W，随后将每个样本平均分成12 个分段经W映射得到局部特征向量，最后对所有局部特征向量求平均计算出100 维的特征向量。

为消除随机性的影响，每组实验均重复进行20次。为了比较所提方法的效果，采用本质成分滤波（对比方法1）［10］、卷积稀疏滤波（对比方法2）［11］、改进权重稀疏滤波（对比方法3）［12］、变体稀疏滤波（对比方法4）［13］、传统稀疏滤波（对比方法5）［8］和振动信号作为输入的所提方法（对比方法6）来处理同一个数据集。其中振动信号是在实验台上与声信号同时采集的，通过振动加速度传感器于轴承座上表面进行采集，采样频率为25.6 kHz。详细的测试结果如图12 所示。所提方法的平均测试准确率为94.88%±0.74%，前5 种对比方法的测试准确率结果分别为 93.27%±1.15%、89.41%±1.32%、87.72%±1.19%、82.12%±1.96%和80.32%±2.02%。可以看出所提方法的准确率度最高，且标准差最低，表明所提方法对轴承故障声信号具有有效且稳定的特征提取能力。值得注意的是对比方法6 的平均准确率为97.73%±0.81%，优于所提方法。是因为振动信号比声信号采集到的故障信息更明显，信噪比更高，所以振动信号的故障诊断准确率也显而易见地比声信号高。但所提方法的准确率也是最接近对比方法6，故提高声信号的诊断精度也是未来的重点研究内容。

图12 测试准确率对比Fig. 12 Comparison of testing accuracies

为了说明并行稀疏滤波的稀疏特征提取性能，随机选取所提方法与五种对比方法对RF2 学习到的100 维特征向量，如图13 所示。可以看到，所有方法学习到的特征主要表现在稀疏性的差异对比上：并行稀疏滤波得到的特征分布具有明显的稀疏性，只有少数特征点具有非零值。经对比方法1 学习到的特征向量的稀疏性略差于并行稀疏滤波，即非零的特征值更多。对比方法2～5 的结果均是非稀疏的，特征向量几乎都没有零值，因此也不利于接下来的故障分类。由此可以看出并行稀疏滤波经2 个不同的归一化方向提取的特征更具有稀疏性，也更有利于实现轴承故障的精确分类。

为了更直观的展示分类效果，采用t-SNE［20］技术对所学的样本特征进行可视化操作，即将100 维的特征向量映射到二维特征空间，通过特征散点图的形式实现分类结果的可视化。经所有方法降维得到的可视化结果如图14 所示。可以看出，所提方法几乎可以区分所有不同轴承健康状态的测试样本，仅IF1、IF3 和RF1 的样本散点有些许混叠现象，其余相同健康状况的样本显示聚类效果较好，具体如图14（a）所示。在图14（b）中，对比方法1 的聚类结果相对差些，仅NC、OF1 和RF3 类型样本显示的可以聚集在一起，其余的轴承故障样本均混合在一起。对比方法2 和对比方法3 的降维结果均表现更差，同样的轴承故障样本均没有聚类完全，且均出现较为严重的混叠现象，如图14（c）和图14（d）所示。对比方法4 和对比方法5的降维结果如图14（e）和图14（f）所示，除了正常状况样本外，其余故障类型样本也均未展现出聚类效果。上述降维结果也与图12 显示的测试准确率结果相应。以上结果表明，所提方法可以根据轴承时域信号特性及诊断任务智能地提取有益于故障诊断的特征。

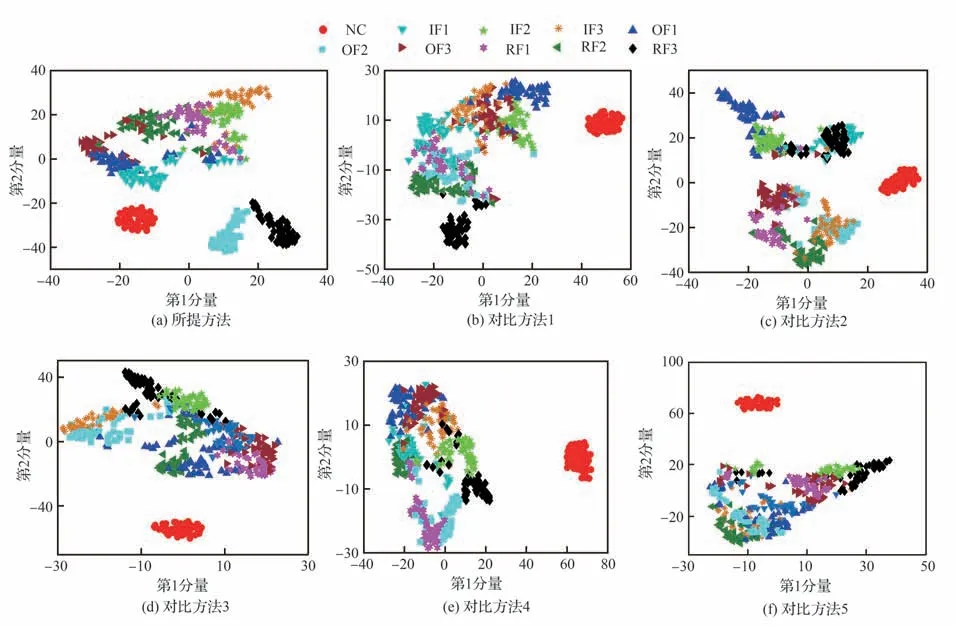
图14 降维结果对比Fig. 14 Comparison of dimension reduction results

5 结 论

提出了一种基于并行稀疏滤波的轴承声信号智能故障诊断方法，所提方法对原始稀疏滤波进行改进经两个不同方向的归一化操作使得模型的特征提取能力得到进一步提高。通过一组仿真实验和一组真实实验数据验证了所提方法的有效性：可以训练出特定的滤波器用于信号的稀疏特征提取，并且在故障诊断过程中不需要任何去噪预处理过程，即可实现不同轴承故障的精准分类，为轴承声信号下的智能故障诊断的工程应用提供了较好的推广价值。虽然所提方法能获得较好结果，但是所提方法的对声信号准确率仍无法与振动信号相媲美，因此提高声信号的诊断精度也是未来的重点研究内容。