预混旋流燃烧火焰三维折射率场重建

李智豪，张彪，李健，许传龙，宋兆龙

东南大学 能源与环境学院 大型发电装备安全运行与智能测控国家工程研究中心，南京 210096

随着航空技术的发展，对航空发动机的性能提出了更高的要求。需要高效率、低排放和高可靠性的航空发动机燃烧室燃烧技术，以满足更为严格的环保和能源高效利用的要求。当前，提高温升、降低污染物排放和提高寿命成为航空发动机燃烧室的发展趋势。因此，发动机旋流燃烧器的设计和研发面临新的挑战［1-2］。旋流燃烧器具有旋流片的特殊结构特点，火焰长度和高温区域更短，燃烧室内湍动能更大，燃气与空气混合更充分，燃烧热效率更高，因此可以有效地提高燃烧性能。现代燃烧室采用旋流方法增强燃料和空气的掺混来保证连续燃烧过程和火焰稳定。旋流燃烧器作为航空发动机燃烧室的关键结构对燃烧过程起到了提高燃烧室涡流强度、提高燃料和空气混合速率、提高火焰稳定性以及减少污染物排放等促进作用［3］。因此旋流燃烧器复杂流场的高精度测量是航空发动机燃烧室设计与改造的重点与难点，需要高分辨率的密度、温度、压力、气体组分浓度等参数的三维信息以分析旋流燃烧器的燃烧性能、动力输出及污染物排放情况，并在此基础上提出优化策略。瞬时三维流场的测量一直是近年来研究的重点，物理接触式测量方法会干扰火焰中的反应和传输过程，而光学诊断方法可以避免该问题，同时可以提供足够的空间分辨率以采集复杂流动中的结构信息，因此具有很高的应用价值。

经过多年的研究与发展，示踪剂与多光谱信号已被用于目标温度和组分的定量分析，测量平面可扫过整个流场区域，从多个角度成像获得准瞬时的体积信息［4］。平面激光诱导荧光技术（Planar Laser Induced Fluorescence， PLIF）是一种测量燃烧反应区域的温度、组分分数等参数以及火焰形貌的有效方法。为了获得湍流火焰的三维结构，体视激光诱导荧光技术（Volumetric Laser Induced Fluorescence， VLIF）将 激 光诱导荧光技术（LIF）与层析技术相结合并应用于瞬态的三维测量［5］。该技术通过多相机同时捕获空间散射的LIF 光子并使用层析重建算法获得组分的空间分布。随着室温和窄线宽半导体激光器的快速发展，可调谐半导体激光吸收光谱（Tunable Diode Laser Absorption Spectroscopy， TDLAS）技术已广泛应用于现场和实时燃烧诊断［6］。通过将TDLAS 与层析技术相结合，可以测量空间的温度和组分浓度分布。窄光谱分辨率使TDLAS 可以对微量气体混合物进行精确测量［7］。然而基于激光的方法成本高且具有复杂的光学、控制和数据采集系统，其安全性问题限制了设备的移动性和测量目标的范围。而且除最近研究的VLIF 技术与三维吸收光谱层析技术外，大多数激光诊断方法仅限于二维测量。背景导向纹影（Background Oriented Schlieren， BOS）是一种基于视在光线积分的流动可视化技术，对折射率梯度较为敏感，而折射率场又可进一步转换为与密度场和温度场。由于折射率场是流体密度和组分的函数，可通过光线偏折的可视化显示流场中的关键结构。BOS 简化了获得有关光偏折信息所需的光学设置，只需要将待研究流动放置在相机和相机聚焦的纹理背景之间即可。技术上易于实现，设备成本相对较低，视场较广且能够在极端条件下进行可靠的测量，因此BOS技术具有很高的研究价值。通过设置多组BOS同步记录流动，可以实现非轴对称非定常流动的三维重建。

BOS方法最早由Dalziel 等［8］在2000 年 提出。这种方法局限性在于其仅检测投射到图像平面上的路径积分信息。对于轴对称流场可使用单相机进行测量，通过泊松方程将时间平均的二维偏移转换为线平均密度，然后通过Abel 逆变换从三维密度场中重建出二维切片。许多后续测试将这种单相机方法用于轴对称目标［9-10］。为了对湍流的三维流动特征进行测量，可将来自多个视图的光线偏折信息与层析成像算法结合以重建三维折射率场，称为背景导向纹影层析（Background Oriented Schlieren Tomography， BOST）。对重建结果进行后处理可获得流动中的局部分子密度、温度、混合物分数或确定燃烧过程中的反应区域［11-12］。Atkinson 和Hancock［13］采用了包括光线偏折识别、折射率梯度重建以及通过泊松积分从梯度推导折射率场的三维非定常流动重建过程提出了首个时间分辨的BOST模型。Nicolas 等［14］提出直接由图像偏移场估算密度场的模型，避免了密度梯度重建的中间步骤，并采用正则化技术来处理不适定问题。BOST 重建是一个不适定的逆问题，逆测量算子会放大噪声，因此必须补充其他信息才能重建折射率场。补充信息的准确性对重建的准确性起很大的作用。Grauer 等［15］采用背景导向纹影层析技术对三维火焰的瞬时折射率场进行重建，验证了不同先验信息对火焰的重建效果。Grauer和Steinberg［16］提出统一的基于光流控制方程的BOST 模型，其无需图像光流场的求解，避免了选择光流计算参数造成的误差且计算成本较低。

本文研究了基于光流方程的BOST 模型中的图像偏移对重建效果的影响，在此基础上采用优化设置对具有复杂结构的湍流火焰进行了折射率场重建模拟，验证采用BOST 技术获取航空发动机燃烧室旋流燃烧器复杂流场三维结构的可行性。

1 背景导向纹影成像模型

1.1 镜头等效光学系统

理想光学系统中任一物点发出的光线经过系统后交于一点，以物点为顶点的同心光束对应于以像点为顶点的同心光束，此时每个物点对应于唯一的共轭像点。对于任何共轴光具组，将其视为理想光学系统，物像之间的共轭关系完全由基点的位置决定［17］。

图1为镜头等效光学系统示意图，理想光学系统的基点包括物方焦点F、像方焦点F'、物方主点H与像方主点H'。平行于光轴的入射光线经过系统交于一点，该点为无限远的位于光轴上的物点的共轭像点即像方焦点。垂直于光轴且经过像方焦点的平面即像方焦面，其共轭平面为无限远的垂直于光轴的物面。共轭像点位于像方无穷远处的物点为物方焦点，垂直于光轴且经过物方焦点的平面为物方焦面，其共轭平面为无限远的垂直于光轴的像面。经过物方焦点的入射光线与其共轭平行光线的延长线存在一交点M，垂直于光轴且经过该交点的平面即物方主面，物方主点则为物方主面与光轴的交点H。作一条与上述经过物方焦点的入射光线的共轭光线高度相等的平行于光轴的光线，这条光线入射理想光学系统得到的出射光线经过像方焦点，这时入射光线与出射光线的延长线也存在一交点M'，垂直于光轴且经过该交点的平面为像方主面，像方主点则为像方主面与光轴的交点H'。M与M'为一对等高点，这对主面的垂轴放大率为+1，即经过共轭点的光线与主面交点的高度相等。

图1 镜头等效光学系统示意图Fig. 1 Schematic diagram of lens equivalent optical system

根据图1 所示的几何关系得到的放大率为

式中：y为背景图案被拍摄区域的尺寸；y'为背景图案被拍摄区域在图像平面对应的尺寸；f与f'分别为物方与像方焦距；s为背景板到物方主面的距离；s'为像方主面到图像平面的距离。

1.2 非均匀介质光线追迹方法

为描述光线的传播过程，建立世界坐标系(x，y，z)作为整个系统的绝对坐标系。为描述在每个相机的图像平面建立图像坐标系(u，v)。在流动区域建立正方体的测量体积，并均匀划分为正方体体素。

光线的传播过程遵循费马定理，在笛卡尔坐标系中的光线传播方程可表示为

式中：r为光线路径上某点的位置坐标(x，y，z)；n为该点的折射率；ds为沿光线的微分距离。定义变量t将式（2）转化为常微分方程，即

使用龙格-库塔公式计算光线路径坐标r，计算步长为Δt，计算步数为i［18］。

龙格-库塔公式的计算步长预先设定且固定不变，需要考虑测量体积边界的情况，避免光线位置超出边界导致误差。利用泰勒公式根据光线与边界的距离计算出所需步长以确定光线与边界的交点位置r及光线离开测量体积时的方向ω［19］。

式中：s0和r0分别表示光线路径离开测量区域范围前一步的位置与坐标，确定光线在测量体积的出射点后即可计算该点所对应的共轭像点的位置。由出射点位置B发出的任意方向的光线均会经过共轭像点，利用该性质可以获得光线与图像平面的交点D，如图2 所示。

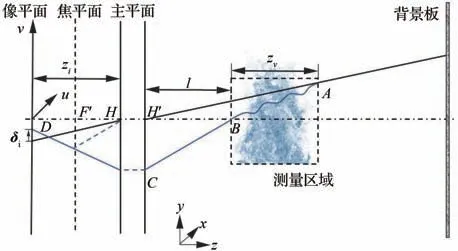
图2 正向过程示意图Fig. 2 Schematic diagram of forward process

图像坐标(Du，Dv)的计算方法为

式 中：Du，v、Cu，v、Bu，v分别为各 点在图像坐标系中u、v方向的坐标；zi为图像平面到像方主面的距离；zii为光线出射点位置B所对应的理想成像距离；M为光线离开测量体积的位置B所对应的理想成像放大率；l为光线离开测量体积的位置B到物方主面的距离。

2 背景导向纹影层析重建方法

2.1 重建模型

由式（2）～式（4）可得

式中：T表示光线在位置r处的方向与折射率的乘积。沿光线对T进行积分可以得到光线经过测量体积后的偏移δ0，即

对于气相介质，其折射率n≈1，因此

对式（8）进行离散化，即

式中：e∈{x，y，z}表示世界坐标系的方向；δ0e为光线经过测量体积后在方向e的偏移；N为测量体积的体素总数；Δsi表示光线在第i个体素中的弦长；(∇en)i表示在第i个体素的折射率梯度。

图3 为逆向过程示意图。为建立光线经过测量体积的偏移δ0与图像偏移δi之间的关系，需要先将三维偏移δ0转换为背景板平面的二维偏移δb。

图3 逆向过程示意图Fig. 3 Schematic diagram of backward process

式中：d为测量体积到背景板的距离；δbu与δbv分别表示图像坐标系中u、v方向的偏移；x、y、z分别表示世界坐标系的3 个方向向量；u、v分别表示图像坐标系的2 个方向向量。

通过成像放大率可将背景板平面的二维偏移δb转换为图像像素偏移δi，即

式中：du、dv为相机u、v方向的像素尺寸；δiu与δiv分别表示图像坐标系中u、v方向的偏移。

由采样的m条光线在n个体素中的弦长以及投影比例M/du，v构成层析投影矩阵SϵRm×n。逆向过程求解所有体素中折射率构成的向量nϵRn，为了得到式（9）中的折射率梯度，采用一阶有限差分矩阵De对折射率向量进行差分运算得到折射率梯度向量［13-14］。

光流定义为在连续图像中观察到的特征点的二维位移。不同图像中的特征通过特定的保持不变的亮度相关联，位移由一组二维向量表示，图像的每个像素对应一个位移向量。光流法假设图像中特征点的亮度不变且位移较小，从而推导出光流的基本约束方程。

式中：I(u，v，t)表示t时刻图像平面(u，v)位置的亮 度；δu、δv、δt分别表 示坐标u、v与时 间的变 化量。背景图案亮度保持不变，忽略介质的吸收与散射，图像在不同时刻的亮度相等且图像像素位移很小，因而可以在BOS 模型中引入式（12）［20］。由于BOS 中只需图像的位移信息，无需根据时间间隔求解运动速度，故采用相同的单位时间步长δt=1 s。式（12）可简化为

结合式（9）～式（13）可得到背景导向纹影层析的重建方程［16］，即

式中：Iu、Iv、It分别表示图像像素亮度在u方向、v方向与时间方向的梯度构成的向量；nv表示布置相机的视角数量；un、vn(n=1，2，…，nv)分别表示每个视角对应的图像坐标系的坐标轴方向向量。

式（14）可整理为最终的矩阵系统，即

2.2 重建算法

由于重建所需的数据中含有测量误差与离散化误差，该超定问题不存在恰好满足An=b的解n。求解大多数适定的超定问题的目标是找到使残差范数最小的唯一最小二乘解nLS=argmin(‖An-b‖2)。当矩阵A为病态矩阵时，测量误差与离散化误差会在解中被放大为大幅度的高频误差分量。因此nLS不是该问题的物理解，需要通过正则化来稳定An=b的反演过程［21］。对于折射率梯度较小的流动，可以采用二阶Tikhonov 正则化获得具有适当范围、空间平滑的折射率场估计，该过程通过最小化以下目标函数实现。

将式（16）整理为

式中：0 表示含有N个零元素的列向量；λ为正则化参数；LϵRN×N为拉普拉斯矩阵，表示相邻体素之间的关系即平滑性条件。

为了确定正则化参数λ的最佳值，以式（16）中的正则项作为数据项‖An-b‖2的函数，选 取不同的正则化参数进行计算并绘制L曲线。L曲线的竖直部分，正则化参数很小，‖An-b‖2也很小，正则化解与扰动后的数据吻合较好，但n对正则化参数的变化较为敏感，属于欠正则化状态，传播的数据误差在总误差中占主导地位；在L曲线的水平部分，正则化参数λ较大，正则化误差占主导地位。随着λ的增大，‖An-b‖2相应增大，但n却几乎不随λ变化，故水平部分属于过正则化状态。为平衡欠正则化与过正则化，在L曲线的曲率最大处选择正则化参数［22］。

为了避免对式（17）中的扩充算子求逆，采用联合代数重建法（Simultaneous Algebraic Reconstruction Technique， SART）求解式（17）中的最小化问题。SART 算法是代数重建算法（Algebraic Reconstruction Technique， ART）的 改 进形式［23］，不同于ART 每次更新时用到一个方程，SART 会先计算所有方程的矫正项，求和之后再应用到变量更新中。由于在每次更新迭代时用到了所有的方程，SART 相较于ART 有更好的抑制重建伪影的作用。SART 算法公式为

式中：n(jk)表示n中第j个元素在第k次迭代时的数值；Q为采样光线总数；N为体素总数。

3 数值模拟

3.1 模拟方法

为了对测量模型进行验证，采用三维高斯温度分布函数建立标准模型对模型误差与重建方法进行基准测试。温度分布函数设置为T(x，y，z)=300+800·exp[ ]-(12x2+3y2+12z2)2（以测量区域底面中心为坐标原点），采用空气的Gladstone-Dale 常数为2.26×10-4m3/kg，压强设置为标准大气压，根据理想气体状态方程获得密度分布后，可利用Gladstone-Dale 方程ρ=(n-1)/G计算对应的折射率场，其中，G为Gladstone-Dale 常数。这种分布会产生规则的光线偏折，从而验证离散测量模型对通过介质的非线性偏折进行近似计算的能力。模拟设置如图4所示，由于折射率场较为简单，采用均匀分布的8 个视角布置相机，每台相机的光轴与相应的纹影背景板垂直。相机的图像探测器分辨率设为512 pixel×512 pixel，重建分辨率为32 pixel×32 pixel×32 pixel。

图4 模拟设置Fig. 4 Simulation setup

考虑到随机点图像中各点之间梯度信息的缺失可能降低光流控制方程的稳定性，因此选用高斯噪声图案作为模拟使用的背景板图案，如图5 所示。

图5 高斯噪声背景图案Fig. 5 Gaussian noise background pattern

由于流动过程中微观涡破碎及旋进涡核运动，旋流燃烧器的结构会对流场造成影响。旋流燃烧器主要设计参数包括喷嘴形式、流量分配、旋流叶片数及安装角度、旋流器级数、内外级旋流数及燃烧室出口收缩比等，会对燃烧室内宏观回流区、流场速度、温度分布及污染物的排放量产生影响。可通过测量获取高分辨率的燃烧室流场三维信息来分析旋流燃烧器对燃烧室的上述影响［24］。因此采用大涡模拟（Large Eddy Simulation，LES）获取了单个旋流燃烧器甲烷预混湍流旋流火焰的温度、密度及各组分浓度信息，并计算得到火焰区域的折射率场，以检验BOST 技术对于旋流燃烧器对象的测量效果。LES 模拟旋流火焰的入口切向速度设为10 m/s，轴向速度为12.5 m/s，甲烷与氧气的质量分数分别设为0.088 与0.212，旋流数设为0.75，以模拟稳定燃烧的强旋流火焰。

利用预设折射率场进行正向过程并进行重建过程的模拟，将重建折射率场与原折射率场进行比较和计算重建误差E，由于折射率接近于1且变化量极小，重建误差的计算式为

式中：nLES表示大涡模拟折射率场；nREC表示重建折射率场。

火焰对象的重建模拟设置采用均匀分布的8个视角布置相机，每台相机的光轴与相应的纹影背景板垂直，图像平面与背景板平板的距离为1 000 mm。由于折射率场较为复杂，相机的图像探测器分辨率设为1 024 pixel×1 024 pixel，测量区域为边长100 mm 的立方体，重建分辨率为50 pixel×50 pixel×50 pixel。为模拟实际应用中的情况，在正向过程获得的图像信息中添加2.5%的测量噪声。

测量体在竖直方向的边界被流动穿过，因此在重建时采用自由边界条件。对于测量体积在水平方向的边界，将边界面的折射率设置为标准状态下干空气的折射率。

3.2 结果与讨论

对高斯分布折射率场的重建结果如图6 所示，重建折射率场与预设折射率场分布基本一致，说明重建采用的离散测量模型对光线通过介质产生的非线性偏折具有较好的计算能力。

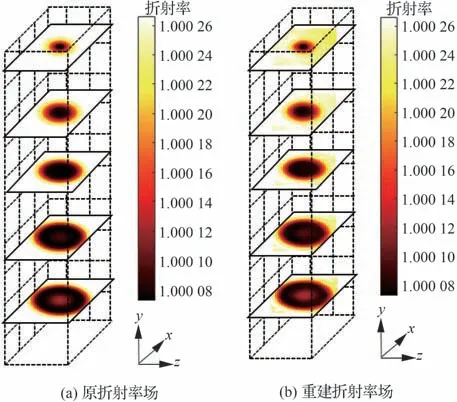
图6 高斯分布折射率场重建Fig. 6 Reconstruction of Gaussian distributed refractive index field

根据图2 及式（6），光线离开测量体的出射点位置与图像像点的位置变化存在如下关系：

式 中：ΔBu，v与ΔDu，v分 别 表 示B、D 这2 点u、v坐标的变化量；zv表示重建区域的尺寸。分析式（20）可知，在参数的实际变化范围内图像的位移随测量体到物方主面的距离l的减小而增大。由2.1 节的分析可知，BOST 方法的重建模型基于光流控制方程，而光流控制方程的推导需要图像偏移较小的假设。另一方面，增大偏移值可以降低识别偏移产生的误差。考虑实际应用中图像的像素偏移大小与测量体的位置、镜头焦距等参数有关，在高斯分布对象对应的设置条件下对不同镜头焦距、处于不同位置的相同折射率场进行了重建模拟，重建误差如图7 所示。

由图7 可知，减小测量区域至相机的距离即增大光线偏折在图像产生的像素位移可以降低重建误差。增大镜头焦距即增大放大率也可增大图像的像素位移，降低重建误差。增大图像位移的优化效果强于由此导致的模型误差的影响。因此实际应用中应在实验设置允许的情况下尽量减小相机至测量体的距离并使用焦距较大的相机镜头。

图7 重建误差Fig. 7 Reconstruction errors

在应用以上讨论的优化设置的基础上，对湍流旋流火焰进行重建的结果如图8 所示，重建折射率场较好地反映出湍流旋流火焰的旋进射流、褶皱和涡旋等结构。分析重建图像可以发现，当采样光线在折射率变化区域穿过的距离较短时，光线的偏折信息更能反应真实的折射率分布；当采样光线在折射率变化区域穿过的距离过长时，影响光线偏折的折射率变化区域较多，光线的偏折信息与图像的位移信息难以反映较大深度范围内的折射率分布。因此火焰边缘区域的折射率场重建效果优于中心区域。

图8 折射率场重建结果Fig. 8 Reconstruction results of refractive index field

依据式（20）对高斯温度分布与LES 模拟对象在采用优化设置条件下进行的一系列模拟重建归一化均方误差在5%以下，重建折射率场与预设折射率场具有较好的一致性。

在获取折射率场的基础上，混合气体的折射率可通过Gladstone-Dale 方程转换为密度，混合气体的密度分布可结合理想气体状态方程进一步得到温度分布的估计。将BOST 技术与其他光学诊断技术结合获得流场中各组分的质量分数分布信息后即可计算温度场参数的准确值。在流场组分信息未知的情况下，可通过折射率变化区域的提取识别燃气分布区域，分别在燃气分布区域与空气环境区域设定不同的Gladstone-Dale 常数，对温度场进行估计。

4 结 论

本文采用背景导向纹影层析技术对湍流火焰的瞬态折射率场进行了重建模拟，主要工作如下：

1）分析了图像偏移大小的影响因素，通过模拟计算了测量体、焦距等设置参数对重建误差的影响，提出了背景导向纹影的优化设置方法。

2）重建结果较好地展示了湍流旋流火焰的复杂结构，说明BOST 技术可应用于在航空发动机旋流燃烧器火焰结构信息的获取。整体重建误差＜5%，测量折射率场与原折射率场较为接近。

3）BOST 技术在精确重建折射率场的基础上可通过Gladstone-Dale 方程与理想气体状态方程进一步得到温度分布的估计。