2022年高考数学北京卷第10题赏析*

⦿北京市第五中学 许文军

1 真题呈现

A.[-5，3] B.[-3，5] C.[-6，4] D.[-4，6]

此题以直角三角形为问题背景，结合单位圆上动点的“动”，带领平面向量数量积的“静”，串联起平面几何的“形”与平面向量数量积的“数”，动静结合，数形转化，展示一幅动人的画卷.

本题难度中等，切入点众多，可以借助平面向量中常用的基底思维、坐标思维以及极化恒等式思维等来展开与应用，实现问题的解决，并在此基础上进一步加以深入与拓展，形成良好的思维习惯，收获更多的知识、思想方法与能力等.

2 真题破解

方法1：基底法.

解后反思：根据平面向量的线性运算，抓住平面图形的几何特征，通过基底的选取与转化，利用平面向量的数量积公式加以展开与转化.再结合平面向量夹角的转化，以及三角函数中辅助角公式的应用，借助三角函数的图象与性质来确定对应的取值范围.基底法是破解平面向量问题最常用的基本技巧方法，也是平面向量中“形”的特征的重要体现.

方法2：坐标法.

解析：如图1所示，以点C为坐标原点，CA，CB所在直线分别为x轴、y轴建立平面直角坐标系xCy，则A(3，0)，B(0，4).

图1

由PC=1，可设P(cosθ，sinθ)，θ∈[0，2π)，则

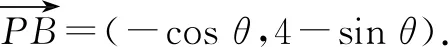
解后反思：根据平面直角坐标系的构建，确定对应点的坐标，借助坐标法合理表示对应的平面向量，通过坐标运算来分析与解决平面向量中的相关问题.坐标法是平面向量“数”的性质的重要体现，以“数”的运算来实现“形”的特征，达到解决问题的目的.

方法3：极化恒等式法.

解析：由△ABC中，AC=3，BC=4，∠C=90°，可得AB=5.

图2

利用平面向量中的极化恒等式，可得

解后反思：根据平面向量中的极化恒等式，将平面向量的数量积由平面向量的线性运算的模导出，合理沟通平面向量的数量积与线性运算之间的联系，是解决平面向量数量积问题的一种有力手段.抓住平面向量中的极化恒等式，建立起平面向量与几何长度(数量)之间的桥梁，有效实现向量与几何、代数的巧妙结合与合理转化，也为问题的深入、拓展与提升提供理论支持.

3 变式拓展

探究1结合以上高考真题以及相应的极化恒等式法的破解，将问题中的数据加以一般化，可以得到下面更具一般性的结论.

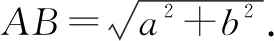
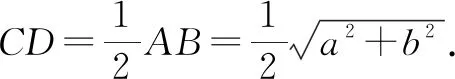
利用平面向量中的极化恒等式，可得

探究2保留高考真题的情境与设置，只改变三角形中角的度数，其他条件不改变，可以得到以下对应的变式问题，考查的基本知识点与能力点更多，难度更大.

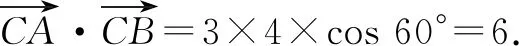
利用余弦定理，可得

图3

利用平面向量中的极化恒等式，可得

4 教学启示

4.1 技巧策略，归纳总结

解决此类平面向量数量积的值、最值或取值范围等问题，常见的技巧策略总结如下：

(1)坐标法.借助平面直角坐标系的合理构建，利用坐标表示与坐标运算，将问题转化为相关的函数(或三角函数)问题来求解.此方法比较容易想到，特别在涉及一些有直角、垂直等要素的平面几何图形时，经常采用此方法来解决.

(2)基底法.借助平面向量基底的合理选择，利用平面向量的线性运算与数量积公式等，结合平面几何特征与图形直观来求解.此方法的关键就是进行平面向量的合理转化，思维量相对复杂一些，也是比较常用的一种方法.

4.2一题多变，深入探究

对于平面向量的一些创新、综合与应用问题，可以合理深入挖掘，形成变式拓展，构建知识网络，从更多层面、更多视角进行深入思考.题目背景、条件要素、结论创设等各个视角都可以加以拓展，真正实现“一题多变”“一题多得”的良好效果，达到做一题、懂一片、会一类，脱离“题海战术”，拓宽数学基础知识，切实提高数学能力，真正达到举一反三、融会贯通的效果.